格值直觉模糊有限自动机的直积与覆盖

杨 莉, 莫智文

(四川师范大学 数学与软件科学学院, 四川 成都 610066)

1965年,L. A. Zadeh[1]提出模糊集理论.随后,在1967年W. G. Wee[2]引入了模糊自动机理论.J. N. Mordeson[3]等对模糊自动机的代数性质做了详细的研究.随着模糊集理论的发展，1983年K. T. Atanassov[4]提出了直觉模糊集，它是一种高层次的模糊集，比一般的模糊集合多了一个非隶属度，这就使得它在处理不确定信息时比传统的模糊集有更强的灵活性和准确性,K. T. Atanassov等[5]又在1984年提出了格值直觉模糊集，格值直觉模糊集理论是直觉模糊集理论的推广.Y. B. Jun[6]于2005年提出了直觉模糊有限自动机的概念,不久Y. B. Jun[7-8]和X. W. Zhang等[9]对直觉模糊有限自动机的代数性质做了详细研究.在此基础上，提出了格值直觉模糊有限自动机的定义，当L=[0,1]时，格值直觉模糊有限自动机就为直觉模糊有限自动机，因此格值直觉模糊有限自动机是直觉模糊有限自动机的推广.自动机的乘积在分解和覆盖定理中起着很重要的作用，因此对自动机乘积的研究是必要的.文献[10-15]建立了自动机的乘积理论.基于此，本文建立了格值直觉模糊有限自动机的直积理论，并得到了一些重要性质.

1 预备知识

特别地，完备格L一定有一最小元和最大元，即infL和supL，分别记为0和1.

定理1.1[17]在任意格L中，下述2个分配恒等式等价：

(D1)a∧(b∨c)=(a∧b)∨(a∧c),∀a,b,c∈L;

(D2)a∨(b∧c)=(a∨b)∧(a∨c),∀a,b,c∈L.

满足分配恒等式D1(或D2)的格L叫做一个分配格.

定理1.2[17]在任意格(L,≤)中，对∀a,b,c∈L有

(L1)a∧a=a,a∨a=a;(幂等律)

(L2)a∧b≤b∧a,a∨b≤b∨a;(交换律)

(L3)a∧(b∧c)≤(a∧b)∧c,a∨(b∨c)≤(a∨b)∨c;(结合律)

(L4)a∧(a∨b)=a=a∨(a∧b).(吸收律)

定理1.3[17]在任意格L中,交、并运算是保序的，即对∀a,b,c∈L，若a≤b，则a∧c≤b∧c,a∨c≤b∨c.

定义1.2[18]′:L→L是格L上的逆序对合对应，即对任意的a,b∈L，a≤b时有a′≥b′且a″=a.

若0,1分别是完备格L的最小元与最大元，则0′=1,1′=0.

定理1.4[18]设L是具有逆序对合对应的完备格，则De Morgan对偶律成立,即对{ai|i∈I}⊂L有

定义1.3[5]设X是一个非空集合，L是具有逆序对合对应的完备格，X上的一个格值直觉模糊集A定义为

A={〈x,μA(x),νA(x)〉|x∈X},

其中μA:X→L,νA:X→L，分别表示X上的元素x属于A的隶属度和非隶属度，′:L→L且对∀x∈X，满足

μA(x)≤(νA(x))′.

格值直觉模糊集A可以简记为A=(μA,νA).

2 格值直觉模糊有限自动机

定义2.1一个格值直觉模糊有限自动机(简写为LIFFSM)是三元组M=(Q,X,A)，其中

1)Q表示非空有限状态集合;

2)X表示非空有限输入符号集合;

3)A=(μA,νA)表示一个Q×X×Q上的格值直觉模糊集，即μA:X→L,νA:X→L,′:L→L且对∀x∈X，满足μA(x)≤(νA(x))′,A叫做格值直觉模糊转移函数.

当L=[0,1]时，格值直觉模糊有限自动机M就为直觉模糊有限自动机，因此格值直觉模糊有限自动机是直觉模糊有限自动机的推广.

令X*表示X上所有有穷长度的串的集合，令Λ表示X*上的空串，对于任意的x∈X*,|x|表示x的长度.

定义2.2若M=(Q,X,A)是格值直觉模糊有限自动机，定义一个Q×X*×Q上的格值直觉模糊集A*=(μA*,νA*)为：对∀q,p∈Q，x∈X*,a∈X,

定理2.1设M=(Q,X,A)为格值直觉模糊有限自动机，则

μA=μA*|Q×X×Q,νA=νA*|Q×X×Q.

定理2.2下列条件相互等价：

1) (L,∨,∧)是分配格，即满足分配恒等式D1(或D2)；

2) 设M=(Q,X,A)为任意格值直觉模糊有限自动机，∀q,p∈Q，x,y∈X*有

3) 设M=(Q,X,A)为任意格值直觉模糊有限自动机，则∀q,p∈Q,x=x1x2…xn∈X*,xi∈X,i=1,2,…,n,有

μA(r1,x2,r2)∧…∧μA(rn-1,xn,p)],

νA(r1,x2,r2)∨…∨νA(rn-1,xn,p)].

证明1)⟹2) 根据y的长度，用数学归纳法证明.

2)⟹1) 取M=(Q,X,A)如下：Q={q0,q1,q2,q3,q4},X={x1,x2,x3},μA(q0,x1,q1)=a,μA(q1,x2,q2)=μA(q1,x2,q3)=1,μA(q2,x3,q4)=b,μA(q3,x3,q4)=c,其余情况取μA(qi,xj,qk)=0.νA(q0,x1,q1)=d,νA(q1,x2,q2)=νA(q1,x2,q3)=0,νA(q2,x3,q4)=e,νA(q3,x3,q4)=f,其余情况取νA(qi,xj,qk)=1.满足a≤d′,b≤e′,c≤f′.

令x=x1,y=x2x3,则有

μA*(q0,xy,q4)=μA*(q0,x1x2x3,q4)=

μA(q0,x1,q1)∧μA*(q1,x2x3,q4),

μA*(q1,x2x3,q4)=

(1∧b)∨(1∧c)=b∨c,

又μA(q0,x1,q1)=a，从而有

μA*(q0,xy,q4)=a∧(b∨c).

又因为

μA*(q0,xy,q4)=μA*(q0,x1x2x3,q4)=

[μA*(q0,x1x2,q2)∧μA(q2,x3,q4)]∨

[μA*(q0,x1x2,q3)∧μA(q3,x3,q4)]=

[μA*(q0,x1x2,q2)∧b]∨

[μA*(q0,x1x2,q3)∧c],

μA*(q0,x1x2,q2)=

μA(q0,x1,q1)∧μA*(q0,x1x2,q3)=

μA(q0,x1,q1)∧μA(q1,x2,q3)=a∧1=a,

从而有

μA*(q0,xy,q4)=(a∧b)∨(a∧c),

则

a∧(b∨c)=(a∧b)∨(a∧c).

即满足分配恒等式D1，则(L,∨,∧)是分配格.

同理可以证明1)⟹3)和3)⟹1).

3 格值直觉模糊有限自动机的直积

定义3.1设Mi=(Qi,Xi,Ai)是格值直觉模糊有限自动机，i=1,2.称M1×M2=(Q1×Q2,X1×X2,A1×A2)为M1与M2的全直积.其中μA1×A2:(Q1×Q2)×(X1×X2)×(Q1×Q2)→L,νA1×A2:(Q1×Q2)×(X1×X2)×(Q1×Q2)→L,∀(q1,q2),(p1,p2)∈Q1×Q2,∀(x1,x2)∈X1×X2，有

μA1×A2((q1,q2),(x1,x2),(p1,p2))=

μA1(q1,x1,p1)∧μA2(q2,x2,p2),

νA1×A2((q1,q2),(x1,x2),(p1,p2))=

νA1(q1,x1,p1)∨νA2(q2,x2,p2).

由定义3.1当X1=X2=X时，可以定义格值直觉模糊有限自动机的限制直积，其定义如下：

定义3.2设Mi=(Qi,X,Ai)是格值直觉模糊有限自动机，i=1,2.称M1∧M2=(Q1×Q2,X,A1∧A2)为M1与M2的限制直积,其中μA1∧A2:(Q1×Q2)×X×(Q1×Q2)→L,νA1∧A2:(Q1×Q2)×X×(Q1×Q2)→L,∀(q1,q2),(p1,p2)∈Q1×Q2,a∈X，有

μA1∧A2((q1,q2),a,(p1,p2))=

μA1(q1,a,p1)∧μA2(q2,a,p2),

νA1∧A2((q1,q2),a,(p1,p2))=

νA1(q1,a,p1)∨νA2(q2,a,p2).

定理3.1设Mi=(Qi,Xi,Ai)是格值直觉模糊有限自动机，i=1,2,则有

1)M1×M2是格值直觉模糊有限自动机;

2)M1∧M2是格值直觉模糊有限自动机,其中X1=X2=X.

证明1) 要证全直积M1×M2为格值直觉模糊有限自动机，只需证A1×A2为格值直觉模糊集.∀(q1,q2),(p1,p2)∈Q1×Q2,∀(x1,x2)∈X1×X2有

μA1×A2((q1,q2),(x1,x2),(p1,p2))=

μA1(q1,x1,p1)∧μA2(q2,x2,p2),

νA1×A2((q1,q2),(x1,x2),(p1,p2))=

νA1(q1,x1,p1)∨νA2(q2,x2,p2),

则

(νA1×A2((q1,q2),(x1,x2),(p1,p2)))′=

(νA1(q1,x1,p1)∨νA2(q2,x2,p2))′=

(νA1(q1,x1,p1))′∧(νA2(q2,x2,p2))′.

因为A1,A2为格值直觉模糊集，所以

μA1(q1,x1,p1)≤(νA1(q1,x1,p1))′,

μA2(q2,x2,p2)≤(νA2(q2,x2,p2))′.

根据任意格L中,交、并运算是保序的，则

μA1(q1,x1,p1)∧μA2(q2,x2,p2)≤

(νA1(q1,x1,p1))′∧(νA2(q2,x2,p2))′,

即

μA1×A2((q1,q2),(x1,x2),(p1,p2))≤

(νA1×A2((q1,q2),(x1,x2),(p1,p2)))′.

所以A1×A2为格值直觉模糊集，则M1与M2的格值直觉直积M1×M2为格值直觉模糊有限自动机.

类似地可证明2).

性质3.1若L为分配格，Mi=(Qi,Xi,Ai)是格值直觉模糊有限自动机，i=1,2.M1×M2为M1与M2的全直积,则对∀(q1,q2),(p1,p2)∈Q1×Q2,∀(x,y)∈(X1×X2)*有

μ(A1×A2)*((q1,q2),(x,y),(p1,p2))=

ν(A1×A2)*((q1,q2),(x,y),(p1,p2))=

证明1) 当|x|=|y|=0时，即x=y=Λ时，

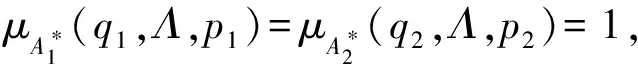
μ(A1×A2)*((q1,q2),(Λ,Λ),(p1,p2))=

μ(A1×A2)*((q1,q2),(Λ,Λ),(p1,p2))=

综上|x|=|y|=0时有

μ(A1×A2)*((q1,q2),(Λ,Λ),(p1,p2))=

同理可证

ν(A1×A2)*((q1,q2),(Λ,Λ),(p1,p2))=

因此，|x|=|y|=0时，结论成立.

2) 若|x|=|y|=n-1(n>0)时，结论成立.

3) ∀(a,b)∈X1×X2,则(xa,yb)∈(X1×X2)*，且|xa|=|yb|=n，则

μ(A1×A2)*((q1,q2),(xa,yb),(p1,p2))=

μ(A1×A2)*((q1,q2),(x,y)(a,b),(p1,p2))=

即|x|=|y|=n时，

μ(A1×A2)*((q1,q2),(x,y),(p1,p2))=

同理可证

ν(A1×A2)*((q1,q2),(x,y),(p1,p2))=

综上所述，结论成立.

性质3.2若L为分配格，Mi=(Qi,X,Ai)是格值直觉模糊有限自动机，i=1,2.M1∧M2为M1与M2的限制直积,则∀(q1,q2),(p1,p2)∈Q1×Q2,∀x∈X*有

μ(A1∧A2)*((q1,q2),x,(p1,p2))=

ν(A1∧A2)*((q1,q2),x,(p1,p2))=

证明利用|x|的长度用数学归纳法证明,方法类似于性质3.1的证明.

4 格值直觉模糊有限自动机的直积之间的覆盖关系

定义4.1设Mi=(Qi,Xi,Ai)是格值直觉模糊有限自动机，i=1,2.如果η:Q2→Q1是一满的部分函数，ξ:X1→X2是一函数，则称序对(η,ξ)是M2对M1的覆盖，记作M1≤M2，如果满足对∀x1∈X1,p,q∈domain(η)有

μA1(η(p),x1,η(q))≤μA2(p,ξ(x1),q),

νA1(η(p),x1,η(q))≥νA2(p,ξ(x1),q).

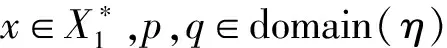
证明根据x的长度，用数学归纳法证明.

1) 当|x|=1时结论显然成立;

2) 假设|x|=n-1时结论成立;

3) 若|x|=n,x=x1x2…xn-1xn,∀xi∈X1则

μA1(r1,xn,η(q))]=

μA1(η(p2),xn,η(q))|η(p2)=r1}≤

μA1(p2,ξ(xn),q)]=

定理4.1设Mi=(Qi,Xi,Ai)是格值直觉模糊有限自动机，i=1,2,3.若M1≤M2,M2≤M3,则M1≤M3.

证明因为M1≤M2,所以存在满的部分函数η1:Q2→Q1,函数ξ1:X1→X2,对∀x1∈X1,p2,q2∈domain(η1)有

μA1(η1(p2),x1,η1(q2))≤μA2(p2,ξ1(x1),q2),

νA1(η1(p2),x1,η1(q2))≥νA2(p2,ξ1(x1),q2).

又因为M2≤M3,所以存在满的部分函数η2:Q3→Q2,函数ξ2:X2→X3,对∀x2∈X2,p3,q3∈domain(η2)有

μA2(η2(p3),x2,η2(q3))≤μA3(p3,ξ(x2),q3),

νA2(η2(p3),x2,η2(q3))≥νA3(p3,ξ(x2),q3).

令η=η1∘η2:Q3→Q1,ξ=ξ2∘ξ1:X1→X3.显然η是一满的部分函数,ξ是一函数,并且对对∀x1∈X1,p,q∈domain(η)⊆domain(η2)有

μA1(η(p),x1,η(q))=

μA1(η1∘η2(p),x1,η1∘η2(q))=

μA1(η1(η2(p)),x1,η1(η2(q)))≤

μA2(η2(p),ξ1(x1),η2(q))≤

μA3(p,ξ2∘ξ1(x1),q)=μA3(p,ξ(x1),q).

同理可证νA1(η(p),x1,η(q))≥μA3(p,ξ(x1),q).因此(η,ξ)是M3对M1的覆盖，即M1≤M3.

定理4.2设Mi=(Qi,X,Ai)是格值直觉模糊有限自动机,i=1,2.则M1∧M2≤M1×M2.

证明定义η:Q1×Q2→Q1×Q2是Q1×Q2上的恒等映射,显然满足η是满的部分函数.定义ξ:X→X×X为，对∀a∈X,有ξ(a)=(a,a)，ξ为一函数,并有

μA1∧A2(η((p1,p2)),a,η((q1,q2)))=

μA1∧A2((p1,p2),a,(q1,q2))=

μA1(p1,a,q1)∧μA2(p2,a,q2)=

μA1×A2((p1,p2),(a,a),(q1,q2))=

μA1×A2((p1,p2),ξ(a),(q1,q2)).

同理可得

νA1∧A2(η((p1,p2)),a,η((q1,q2)))=

νA1×A2((p1,p2),ξ(a),(q1,q2)).

则(η,ξ)是M2对M1的覆盖，即M1∧M2≤M1×M2.

定理4.3设Mi=(Qi,Xi,Ai)是格值直觉模糊有限自动机，i=1,2,3.若M1≤M2，则

1)M1×M3≤M2×M3,M3×M1≤M3×M2;

2)M1∧M3≤M2∧M3,M3∧M1≤M3∧M2,其中X1=X2=X3=X.

证明因为M1≤M2,所以存在满的部分函数η1:Q2→Q1,函数ξ1:X1→X2,对∀x1∈X1,p2,q2∈domain(η1)有

μA1(η1(p2),x1,η1(q2))≤μA2(p2,ξ1(x1),q2),

νA1(η1(p2),x1,η1(q2))≥νA2(p2,ξ1(x1),q2).

定义η2:Q2×Q3→Q1×Q3为对∀p2∈Q2,p3∈Q3有η2((p2,p3))=(η2(p2),p3),易知满足η2是满的部分函数.定义ξ2:X1×X3→X2×X3为，对∀x1∈X1,x3∈X3有ξ2((x1,x3))=(ξ1(x1),x3)，显然ξ为一函数.由任意格L中交、并运算是保序的,定义3.1和定义4.1,易知(η2,ξ2)是M2×M3对M1×M3的覆盖,即M1×M3≤M2×M3.同理可证M3×M1≤M3×M2,进而可证M1∧M3≤M2∧M3,M3∧M1≤M3∧M2.

推论4.1设Mi=(Qi,Xi,Ai)是格值直觉模糊有限自动机，i=1,2,3.若M1≤M2，则

1)M1∧M3≤M2×M3,其中X1=X3=X;

2)M3∧M1≤M3×M2,其中X1=X3=X.

证明利用定理4.1，定理4.2和定理4.3即可得证.

推论4.2设Mi=(Qi,Xi,Ai)是格值直觉模糊有限自动机，i=1,2,3,4.若M1≤M2，M3≤M4,则

1)M1×M3≤M2×M4;

2)M1∧M3≤M2∧M4,其中X1=X2=X3=X4=X;

3)M1∧M3≤M2×M4,其中X1=X3=X.

证明1)和2)的证明利用定理4.1和定理4.3即可得证.3)的证明利用定理4.1和此推论中的1)得证.

5 结语

本文在格值直觉模糊集的框架下,给出了格值直觉模糊有限自动机的定义.格值直觉模糊有限自动机是直觉模糊有限自动机的推广.因此对格值直觉模糊有限自动机进行研究是有必要的.自动机的乘积是自动机研究的一个重要方面.本文系统的研究了格值直觉模糊有限自动机在全直积和限制直积下的转移函数性质、覆盖关系和覆盖关系的传递性质，为进一步研究格值直觉模糊有限自动机奠定了一定的理论基础.对格值直觉模糊有限自动的乘积研究还有很多工作可以做，比如，格值直觉模糊有限自动机的级联积、圈积、同态和弱覆盖等,这些将是今后工作的主要内容.

[1] Zadeh L A. Fuzzy sets[J]. Information and Control,1965,8(3):338-353.

[2] Wee W G. On generalizations of adaptive algorithm and application of the fuzzy sets concept to pattern classification[D]. West Lafayette:Purdue University,1967.

[3] Mordeson J N, Malik D S. Fuzzy Automata and Languages: Theory and Applications[M]. Boca Raton,London:Chapman & Hall/CRC,2002.

[4] Atanassov K T. Intuitionistic Fuzzy Sets[J]. Fuzzy Sets and Systems,1986,20:87-96.

[5] Atanassov K T, Stoeva S. IntuitionisticL-fuzzy sets[C]// Trappl R. Cybernetics and Systems Research. Amsterdam:North-Holland,1984:539-540.

[6] Jun Y B. Intuitionistic fuzzy finite state machines[J]. J Appl Math Comput,2005,17(1/2):109-120.

[7] Jun Y B. Intuitionistic fuzzy finite switchboard state machines[J]. J Appl Math Comput,2006,20(1/2):315-325.

[8] Jun Y B. Intuitionistic fuzzy transformation semigroups[J]. Information Sciences,2007,177:4977-4986.

[9] Zhang X W, Li Y M. Intuitionistic fuzzy recognizers and intuitionistic fuzzy finite automata[J]. Soft Comput,2009,13:611-616.

[10] 冯文俊,易忠,邓培民. 状态机和变换半群积的覆盖关系[J]. 广西师范大学学报:自然科学版,2007,25(1):26-29.

[11] 刘军,莫智文. 格值有限自动机的乘积[J]. 高校应用数学学报,2009,24(1):121-126.

[12] 胡忠刚,邓培民,易忠. 模糊树自动机的积与覆盖[J]. 广西师范大学学报:自然科学版,2009,27(4):31-35.

[13] Liu J, Mo Z W, Qiu D, et al. Products of Mealy-type fuzzy finite state machines[J]. Fuzzy Sets and Systems,2009,160(16):2401-2415.

[14] 翁福利,舒兰,王泽文. 直觉模糊有限自动机的乘积[J]. 模糊系统与数学,2012,26(4):84-88.

[15] 柏明强. Fuzzy树自动机的等价性[J]. 四川师范大学学报:自然科学版,2009,32(1):13-16.

[16] Birkhoff G. Lattice Theory[M]. 3rd Ed. Providence RI:AMS Colloquium Publications,1979.

[17] 胡长流,宋振明. 格论基础[M]. 开封:河南大学出版社,1990.

[18] 王国俊. 映射与逆映射[J]. 商洛师范专科学校学报,1999,10(4):1-7.