Zerosumfree半环上半线性空间的基

罗 琳, 王学平

(四川师范大学 数学与软件科学学院, 四川 成都 610066)

半环上的矩阵理论应用相当的广泛,其研究也已有相当长的历史(参见文献[1-12]).一方面,展开了半环上矩阵可逆的研究,如:1952年,Luce讨论了布尔代数(一类特殊的半环)上的布尔矩阵,并给出布尔矩阵可逆的充要条件是它是一个正交矩阵(见文献[11]).自此以后,半环上逆矩阵的研究得以迅速展开,如:1963年,D. E. Rutherford[13]给出了布尔矩阵可逆的其他充要条件;1964年,Y. Give’on[14]研究了分配格(一类特殊的半环)上的可逆矩阵;1984年,C. Reatenauer等[7]讨论了交换半环上的可逆矩阵.另一方面,Zerosumfree半环上半线性结构的研究也有相当悠久的历史.1979年,Cuninghame-Green在Min-plus代数上建立了一系列类似于线性代数的理论,如线性方程、特征值问题、线性相关与无关、秩及维数等.之后,许多学者就开始对Zerosumfree半环上的半线性空间进行了深入的研究(可见文献[15-16]).2007年,Y. J. Tan[9]探讨了Antirings(Zerosumfree半环)上矩阵的可逆问题,给出了矩阵为可逆矩阵的一些充要条件;同年,A. Di Nola等应用半环和半模的概念介绍了MV-代数上的半线性空间,同时获得了类似于经典线性代数中的相关结论(见文献[8]).但是线性空间中基的一些结论还未得到解决,其中一个就是:是否每个基都具有相同的基数.这个问题在Max-plus代数上已经得到了肯定的回答(见文献[1]).2010年,S. Zhao等[17-18]给出了并半环(一种特殊的Zerosumfree半环)上基具有相同基数的充要条件.次年,Q. Y. Shu等[19]对Zerosumfree半环进行了深入研究,并给出了半线性空间上基的个数相同的充要条件.在本文中,将进一步研究Zerosumfree半环上n维向量半线性空间中基的个数问题,给出基数都为n的等价条件及基的范围.

1 预备知识

定义1.1[10,20]设L是一非空集合,如果在L中有2个代数运算+和·满足:

(i) (L,+,0)是交换幺半群;

(ii) (L,·,1)是幺半群;

(iii)r·(s+t)=r·s+r·t,(s+t)·r=s·r+t·r,∀r,s,t∈L;

(iv) 0·r=r·0=0,∀r∈L;

(v) 0≠1,

若L中任意的r,r′有r·r′=r′·r,则称半环=〈L,+,·,0,1,〉为交换半环;若r+r′=0,则一定有r=r′=0称该半环为Zerosumfree半环.若L中元r满足对∀a,b∈L,r=a+b蕴含r=a或r=b,则称r为可加既约元.

例1.1设R为实数集,若∀a,b∈R∪{-∞}满足a+b=max{a,b},a·b=a+b(此处的“+”是普通的实数加法),则=〈R∪{-∞},+,·,{-∞},0〉是交换半环.

注1.1半环=〈R∪{-∞},+,·,{-∞},0〉就是通常所指的Max-plus代数(见文献[15]).

例1.2设M是交换幺半群,若EndM={f:f:M→M满足f(x+y)=f(x)+f(y),∀x,y∈M},∀f,g∈EndM,定义运算:

(f+g)(x)=f(x)+g(x),

(f·g)(x)=f(g(x)),

则EndM是交换半环.

例1.3自然数集N对于通常整数间的加法和乘法是交换Zerosumfree半环.

例1.4[0,1]关于运算a+b=max{a,b}和a·b=min{a,b},非负整数关于普通的加法和乘法运算,非负整数集关于运算a+b=g.c.d{a,b}和a·b=l.c.m{a,b}(其中,g.c.d(l.c.m){a,b}代表a与b的最大(或最小)公因子(或公倍数))都是交换Zerosumfree半环.

定义1.2[20]设=〈L,+,·,0,1,〉是一个半环,=〈A,+A,0〉为一个加法交换幺半群.若存在映射*:L×A→A满足:∀r,r′∈L,a,a′∈A,

1) (r·r′)*a=r*(r′*a);

2)r*(a+Aa′)=r*a+Ar*a′;

3) (r+r′)*a=r*a+Ar′*a;

4) 1*a=a;

5) 0*a=r*0A=0A,

则称为左-半模.右-半模可类似的定义.在此就不累述.

定义1.3[8]设=〈L,+,·,0,1,〉为半环,则称上的半模为-半线性空间.

注1.2定义1.3中的半模即是指左-半模或右-半模[10].

通常,称半线性空间的元素为向量;称半环上的元素为标量(或者系数).前者用黑体表示以区分标量.为方便起见,假设以下均为左-半模.记于是可建立-半线性空间如下:

例1.5设=〈L,+,·,0,1,〉是一个半环,其中(x1,x2,…,xn)T是(x1,x2,…,xn)的转置,对∀x=(x1,x2,…,xn)T,y=(y1,y2,…,yn)T∈Vn(L),r∈L,定义2种运算:

x+y=(x1+y1,x2+y2,…,xn+yn)T,

r*x=(r·x1,r·x2,…,r·xn)T.

0n×1=(0,0,…,0)T.显然Vn=〈L,+,·,0,1;*;Vn(L),+,0n×1〉是-半线性空间.

定义1.4[8]在半线性空间=〈L,+,·,0,1;*;A,+A,0A〉中,称下面的表达式

λ1a1+Aλ2a2+A…+Aλnan

定义1.5[8]在-半线性空间,单个向量a是线性无关的.若向量组a1,…,an(n≥2)中任一向量都不能由其余向量线性表出,则称a1,…,an是线性无关的,否则称a1,…,an是线性相关的.若无限集合的任意有限子集都是线性无关的,则此无限集合是线性无关的.

注1.3半线性空间或半模上的线性相关和线性无关还有其他定义(见文献[1-2,10,16]).

若半线性空间的每个元都是其非空子集G中元素的线性组合,则称G是半线性空间的生成集(见文献[1]).

定义1.6[10]设为-半线性空间,则称中线性无关的的生成集为中的基.

例1.6=〈L,+,·,0,1〉为例1.4中最后一个半环.在-半线性空间V2中,向量组和向量组都是V2的基.

λA=(λ·aij)m×n,

则〈Mn(L),+,·,0n,In〉是一个半环,其中

注1.4Mm×n(L)中的置换矩阵,对角矩阵等相关概念都可依照经典线性代数来定义.在此就不赘述.

引理1.1[19]1)-半线性空间Vn中,若仅有1是乘法可逆元,则每个基的基数相同当且仅当1是L中的可加既约元.

定义1.7设=〈L,+,·,0,1,〉是交换Zerosumfree半环,r∈L.若存在{pt∈L:t∈T}⊆L{0}使得则称为元r的分解.进一步,若对∀t0∈T,∀则称该分解是不可约的.

注1.5在定义1.7中,若|T|<∞,则称r有|T|个元的有限不可约分解.

例1.7设L=[0,1]2,定义任意(a,b),(c,d)∈L,(a,b)≤(c,d)当且仅当a≤c,b≤d,规定运算:(a,b)+(c,d)=(max{a,c},max{b,d});(a,b)·(c,d)=(min{a,c},min{b,d}).由定义1.7,很容易得到=〈L,+,·,(0,0),(1,1)〉是交换Zerosumfree半环.(1,1)=(1,0)+(0,1),所以(1,1)有不可约有限分解,不难看出(1,1)并无超过2个元素的不可约分解.

例1.8=〈N,+,·,0,1,〉是自然数集Zerosumfree半环.若其运算为例1.4中定义的运算,p1,p2,…,pn是互不相同的素数,则是1的包含n个元素的不可约分解.

例1.9若L是非负整数集,∀a,b∈L满足运算:a+b=g.c.d{a,b};a·b=l.c.m{a,b},则〈L,+,·,0,1〉是一个交换Zerosumfree半环.在V3=〈V3(L),+,03×1〉中,若a+b=1,则(1,0,0)T=(a,0,0)T+(b,0,0)T,所以(1,0,0)T有不可约分解.

易得{e1,e2,…,en}是Vn的一组基,其中

e1=(1,0,…,0),e2=(0,1,…,0),…,

en=(0,0,…,1).

通常称{e1,e2,…,en}是Vn的一组标准基.

2 半线性空间Vn中的基数

引理2.1若1有t个元素的有限不可约分解,则Vn中存在一组基的基数为nt.

b1=(b1,0,…,0),b2=(b2,0,…,0),…,

bt=(bt,0,…,0),bt+1=(0,b1,…,0),…,

b2t=(0,bt,…,0),…,

b(n-1)t=(0,0,…,b1),…,bnt=(0,0,…,bt).

下面将证明{b1,b2,…,bnt}是Vn的一组基.事实上,

(1)

而{e1,e2,…,en}是Vn的一组标准基,因此任意向量a∈Vn,存在系数λ1,λ2,…,λn∈L,使得

a=λ1e1+λ2e2+…+λnen.

(2)

由(1)与(2)式可以推出:

引理2.2若1有t个元素的有限不可约分解,则1一定含有t-1个元的不可约分解.

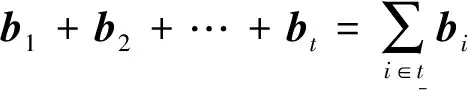
引理2.3若1有t个元素的有限不可约分解,则Vn中存在一组基的基数为nt-1.

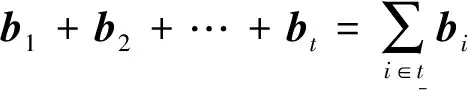
c=(c,0,…,0),b3=(b2,0,…,0),…,

bt=(bt,0,…,0),bt+1=(0,b1,…,0),…,

b2t=(0,bt,…,0),…,b(n-1)t=(0,0,…,b1),

…,bnt=(0,0,…,bt).

类似于引理2.1的证明,亦可证明c,b3,…,bnt是Vn的一组基.得证.

注2.1k(L)=1当且仅当若1=a+b则有a=1或b=1.

定理2.1如果k(L)=q是有限的,则Vn中基的基数为n到nq中所有的整数.

例2.1考察如上图所示格L,∀x,y∈L,定义x+y=x∨y,x·y=x∧y,其中∨(∧)代表并(交).显然L={0,a,b,1}不是线性的,且k(L)=2.半线性空间V2=〈L2,+,·,(0,0),(1,1)〉的基有:{(0,1)T,(1,0)T};{(a,0)T,(b,0)T,(1,0)T};{(a,0)T,(b,0)T,(0,a)T,(0,b)T}.

推论2.1设=〈L,+,·,0,1,〉是交换Zerosumfree半环.若k(L)=+∞,则对每一个自然数m≥n,Vn都有一组基的基数为m.

e1=(1,0,…,0,0),e2=(0,1,…,0,0),…,

en-1=(0,0,…,1,0),b1=(0,0,…,0,b1),

b2=(0,0,…,0,b2),…,

bt=(0,0,…,0,bt),bt+1=(0,0,…,0,c).

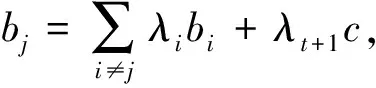
综上,e1,e2,…,en-1,b1,…,bt+1是Vn的一组基,基数为t+1,定理得证.

下面将继续研究半线性空间Vn的基数是唯一确定的充分必要条件.

定义2.1[19]设r,a,b∈L,若r=a+b蕴含r=a或r=b，则称r是半环中的可加既约元.

定理2.2在半线性空间Vn中,下面的条件是等价的:

1) 1是可加既约元;

2)Vn中每个向量可唯一的线性表出;

3)Vn中每个单位向量可被唯一的线性表出;

4)k(L)=1;

5) 每组基都有相同的基数.

证明1)⟺5),2)⟺5)可见证明[19].由k(L)的定义可知4)⟹1),显然3)⟺2)所以此定理成立.

注2.2由定理2.2可以得到:

1) 若1∈L是并既约元,则半线性空间Vn的基的基数为n;

2) 若L是线性完备格,则半线性空间Vn的基的基数为n;

3) 若L是完备格,k(L)=q,则Vn中的基的基数为n到nq中的整数.

[1] Cuninghame-Green R A, Butovic P. Bases in max-algebra[J]. Linear Algebra Appl,2004,389:107-120.

[2] Gregory D A, Pullman N J. Semiring rank: Boolean rank and nonnegative rank factorization[J]. J Combin Info Syst Sci,1983,8(3):223-233.

[3] Ghosh S. Matrices over semirings[J]. Information and Sciences,1996,90:221-230.

[4] Beasley L B, Lee S G. Linear operations strongly preservingr-potent matrices over semirings[J]. Linear Algebra Appl,1992,162/163/164:589-599.

[5] Minoux M. Bideterminants arborescences and extension of the matrix-tree theorem to semirings[J]. Discrete Math,1997,171:191-200.

[6] Poplin P L, Hartwig R E. Determinantal identities over commutative semirings[J]. Linear Algebra Appl,2004,378:99-132.

[7] Reutenauer C, Straubing H. Inversions of matrices over a commutative semiring[J]. J Algebra,1984,88:350-360.

[8] Di Nola A, Lettieri A, Perfilieva I, et al. Algebraic analysis of fuzzy systems[J]. Fuzzy Sets and Systems,2007,158:1-22.

[9] Tan Y J. On invertible matrices over antirings[J]. Linear Algebra Appl,2007,423:428-444.

[10] Golan J S. Semirings and Their Applications[M]. Dordrecht:Kluwer Academic Publishers,1999.

[11] Baccelli F, Mairesse J. Ergodic theorems for stochastic operators and discrete event networks[C]//Gunawardena J. Idempotency. Cambridge:Cambridge University Press,1998,11:171-208.

[12] Gondran M, Minoux M. Dioids and semirings: links to fuzzy sets and other applications[J]. Fuzzy Sets and Systems,2007,158:1273-1294.

[13] Rutherford D E. Inverses of Boolean matrices[J]. Proceedings of the Glasgow Mathematical Association,1963,6:49-53.

[14] Give’on Y. Lattice matrices[J]. Inform Control,1964,7:477-484.

[15] Butkovic P. Max-algebra: the linear algebra of combinatorics[J]. Linear Algebra Appl,2003,367:313-335.

[17] Zhao S, Wang X P. Invertible matrices and semilinear spaces over commutative semirings[J]. Information Sciences,2010,180:5115-5124.

[18] Zhao S, Wang X P. Bases in semilinear spaces over join-semiring[J]. Fuzzy Sets and Systems,2011,182:93-100.

[19] Shu Q Y, Wang X P. Bases in semilinear spaces over Zerosumfree semirings[J]. Linear Algebra Appl,2011,435:2681-2692.

[20] Zimmermann U. Linear and combinatorial optimization in ordered algebraic structures[C]//Annals of Discrete Mathematices. Amsterdam:North-Holland,1981:10.