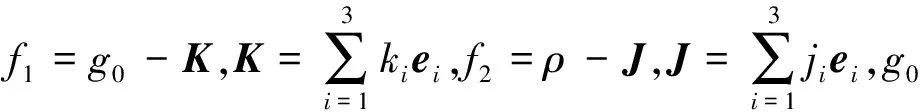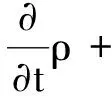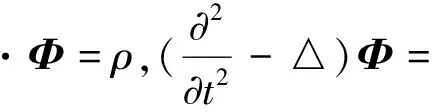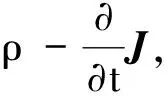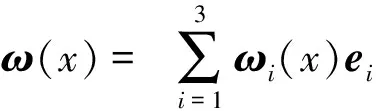磁单极子存在时的Maxwell方程组的初边值问题
王治蓉, 杨丕文*, 李又超
(1. 四川师范大学 数学与软件科学学院, 四川 成都 610066; 2. 东方电气集团 东方电机有限公司, 四川 德阳 618000)
Maxwell方程组是电磁理论的核心,描述了宏观电磁现象,方程组的微分形式为
(1)
方程组(1)的4个方程表示的物理意义在文献[1]中有详细的解释.此方程组表明自然界中存在着作为场源的电荷和电流,不存在磁荷与磁流,即磁单极子不存在.理论和实验却说明磁单极子存在,国内外都有一些关于磁单极子的研究[2-9].
如果磁单极子存在,设磁荷密度为g0,磁流密度为K,与处理电荷的方法类似,磁流密度K与磁荷密度g0满足连续性方程
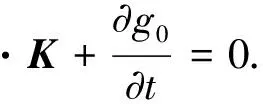
(2)
方程组(1)中的第一与第二式可改写为
▽·B=g0,
(3)
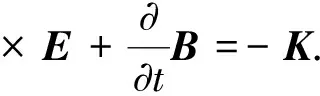
(4)
方程组(1)中第三与第四式在磁荷存在时仍然成立.
因此,磁单极子存在时,得到一组新的Maxwell方程组为
(5)
设C=1,ε0=μ0=1,E=Φ,H=Ψ, Maxwell方程组(1)与方程组(5)即可简化为[10-11]
(6)
(7)
引入拟四元数空间[12],即记二阶矩阵
则有
e2e3=-e3e2=-ie1,e3e1=-e1e3=-ie2.
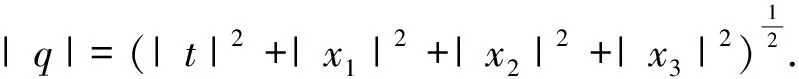
引入一阶微分算子
▽,
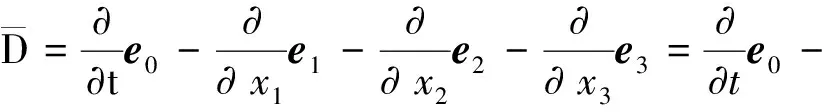
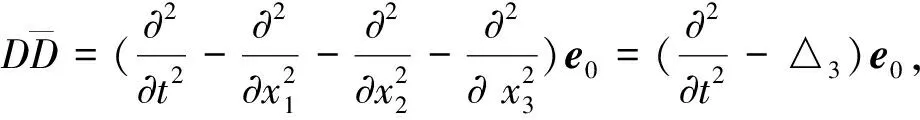
在文献[12]中讨论了某些一阶双曲方程组的初边值问题,用类似的方法,在文献[13]中讨论了Maxwell方程组(6)的初边值问题,而在文献[12]中引入了拟四元数空间后,Maxwell方程组(6)可表示为
D(ψ+iΦ)=if2,
(8)
而方程组(7)可表示为
D(ψ+iΦ)=f1+if2,
(9)
而方程组(7)是磁单极子存在时的Maxwell方程组,下面就讨论此方程组的初边值问题.为了简化计算,先讨论方程
▽)(ψ+iΦ)=-K+i(ρ-J)
2 方程▽)(ψ+iΦ)=-K+i(ρ-J)的初边值问题
设G是R4中的一个区域,考虑G上关于(ψ+iΦ)的方程
▽)(ψ+iΦ)=-K+i(ρ-J), (10)
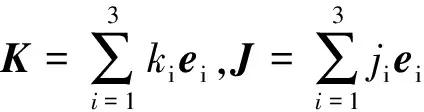
(11)
记Ω={(t,x)||x|<1-t,0 (φ2e0+iφ3e1)(0,x)=f2e0+if3e1, (12) φ1(0,0,x2,x3)=f1(x2,x3), (13) ψ1(0,x)=τ(x),x∈∂B3, (14) Re(x2e0-ix3e1)κ[ψ2(0,0,x2,x3)e0+ iψ3(0,0,x2,x3)e1]=r(x2,x3)e0, (15) 其中 ω(x)=ω1+(ω2e0+iω3e1)e2, (16) (17) 2)当κ< 0时,问题可解,当且仅当r′(ζ)满足条件 m=1,2,3,…,-κ-1. (18) 当此条件满足时,其解仍如结论(1)中式子表示,但其中ψ(t,x)中的ω(x)=ω1e0+(ω2e0+iω3e1)e2,ω1与结论(1)中表示一致,而 (19) 从而可以推出方程(10)及方程组(11)的相容性条件 ▽·J=0, (20) 方程(20)在电动力学中被称为电荷守恒方程[14],以下恒假设ρ及J满足此方程. 定理1对锥形区域ω上的满足方程组 (21) 的向量函数Φ(t,x)的初始条件(12)和(13)的Cauchy问题,有且仅有唯一的解 (22) 其中 (24) (25) (26) 证明由(23)和(24)式知,φ2,φ3满足方程及初始条件[15] (27) (28) 而C(t,x2,x3)满足方程 (29) 由(25)式与(27)、(28)式,可得 则 从而 即得φ1(t,x)满足方程(30). 将方程(10)化成关于向量函数ψ的方程组 (31) 由此可得定理2. (32) 其中ω(x)是满足方程▽ω=0的任一向量函数. τ″(x),x∈∂B, Re(x2e0-ix3e1)κ[ω2(0,0,x2,x3)e0+iω3(0,0,x2,x3)e1]= r(x2,x3)e0-im(x2e0-ix3e1)κ× r″(x2,x3)e0, (x2,x3)∈Г . 定理3(1)当κ≥ 0时,Ω上的方程(10)的问题F有解ψ+iΦ,其中Φ(t,x)如(22)式所示,ψ(t,x)如式(32)所示,ω(x)类似于式(16)和式(17)表示,仅分别用τ″(x)和r″(x2,x3)代替其中的τ′(x)和r′(x2,x3). (2)当κ< 0时,Ω上的方程(10)的问题F可解,当且仅当r″(ζ)如r′(ζ)满足条件(18),当这些条件满足时,其解ψ+iΦ仍由(22)式与(32)式表示,ψ(t,x)中的ω(x)由τ″(x)和r″(x2,x3)代替(19)式中的τ′(x)和r′(x2,x3). 设G是R4中的一个区域,考虑G上关于(ψ+iΦ)的方程 ▽)(ψ+iΦ)=f1+if2, (33) (34) (34)式即为磁单极子存在时的Maxwell方程组. 从而可以推出方程(33)及方程组(34)中的g0、K、ρ、J满足条件 ▽·K=0, (35) (36) 方程(35)和(36)在电动力学中被称为磁荷守恒方程和电荷守恒方程,以下恒假设g0、K、ρ、J满足方程(35)和(36).对锥形区域Ω上的满足方程组 的向量函数Φ(t,x)的初始条件(12)和(13)的Cauchy问题,有且仅有唯一的解 (38) 其中φ2、φ3、φ1如定理1的(23)~(26)式. 将方程(33)化成关于向量函数ψ的方程组 由此可得定理4. 定理4关于Ω上的向量函数ψ(t,x)的方程组(39)可解的充要条件是Φ(t,x)满足(21)式中的 当此条件满足时,其一般解可表示为 ▽×Φ)(ζ,x)dζ+T3[g0- (40) 其中ω(x)是满足方程▽ω=0的任一向量函数. τ‴(x),x∈∂B, Re(x2e0-ix3e1)κ[ω2(0,0,x2,x3)e0+ iω3(0,0,x2,x3)e1]=r(x2,x3)e0-im(x2e0-ix3e1)κ× r‴(x2,x3)e0, (x2,x3)∈Г. 定理51) 当κ≥ 0时,Ω上的方程(33)的问题F有解ψ+iΦ,其中Φ(t,x)如(38)式所示,ψ(t,x)如(40)式所示,ω(x)类似于(16)和(17)式表示,仅分别用τ‴(x)和r‴(x2,x3)代替其中的τ′(x)和r′(x2,x3). 2) 当κ<0时,Ω上的方程(33)的问题F可解,当且仅当r‴(ζ)如r′(ζ)满足条件(18),当这些条件满足时,其解ψ+iΦ仍由(38)与(40)式表示,ψ(t,x)中的ω(x)由τ‴(x)和r‴(x2,x3)代替 (19)式中的τ′(x)和r′(x2,x3). 磁单极子存在时,电磁关系发生改变,定理5的结论即为磁单极子存在时的Maxwell方程组的初边值问题在不同情况下的解,其中的Φ、ψ即为电场强度和磁场强度函数. [1] Maxwell, Clerk J. A dynamical theory of the electromagnetic field[J]. Philosophical Transactions of the Royal Society of London,1865,155:459-512. [2] 刘光华,邓小燕. 磁单极子进展概述[J]. 大学物理,2010,29(11):1-5. [3] 胡永红,毛彩霞. 旋转磁单极子场方程的研究[J]. 华中师范大学学报:自然科学版,2012,46(2):152-154. [4] 胡陈果. 推导包括磁荷的麦氏方程组的新方法[J]. 四川师范大学学报:自然科学版,1994,15(1):89-93. [5] 宫蒂. 含磁荷磁流麦氏方程组解的特性[J]. 中山大学学报:自然科学版,1995,34(1):106-109. [6] Morris D J P, Tennant D A, Grigera S A, et al. Dirac strings and magnetic monopoles in spin Ice Dy2Ti2O7[J]. Science,2009,326:411-414. [7] Giblin S R, Bramwell S T, Holdsworth P C W, et al. Creation and measurement of long-lived magnetic monopole currents in spin ice[J]. Nature Physics,2011,7:252-258. [8] Bonitz M. Spin ice:a plasma of magnetic monopoles[J]. Nature Physics,2011,7:192-194. [9] Mengotti E, Heyderman L J, Rodríguez A F, et al. Real-space observation of emergent magnetic monopoles and associated Dirac strings in artificial kagome spin ice[J]. Nature Physics,2010,7:68-74. [10] 陈池一,李康. Maxwell理论的电磁对偶性[J]. 浙江大学学报:自然科学版,2001,28(1):27-34. [11] 卢里·D. 粒子和场[M]. 董明德,译. 北京:科学出版社,1981. [12] 杨丕文,李曼荔,陈颖. 某些一阶双曲方程组的初边值问题[J]. 应用数学学报,2008,31(1):61-70. [13] Yang P W, Yang S, Li M L. An initial-boundary value problem for the maxwell equations[J]. J Diff Eqns,2010,249:3003-3023. [14] 郭硕鸿. 电动力学[M]. 北京:高等教育出版社,1984. [15] 柯朗, 希尔伯特. 数学物理方程[M]. 北京:科学出版社,1977 [16] Yang P W. The Riemann-Hilbert boundary value problem for the Moisil-Theodorsco system[J]. Acta Math Sci,2006,26 (7):1057-1063. [17] 杨丕文,杨硕. 可换四元数空间中某些双曲型方程的Riemann-Hilbert边值问题[J]. 数学学报,2008,51(1):171-180. [18] 杨丕文,李曼荔,杨硕. 在可交换四元数空间中的双曲型方程的特征边值问题[J]. 数学学报,2007,50(6):1249-1256. [19] 杨丕文. 四元数正则函数的某些函数论性质[J]. 应用数学学报,2010,33(6):1095-1112. [20] 杨丕文,李曼荔.n阶Moisil-Theodoresc型方程的Riemann-Hilbert边值问题[J]. 数学学报,2010,53(3):585-596. [21] 蒲松,杨丕文. 双解析函数的非正则型及非齐次二阶方程的某些边值问题[J]. 四川师范大学学报:自然科学版,2007,30(3):295-299. [22] 杨丕文. 双圆柱区域上的高阶四元数函数的Dirichlet边值问题[J]. 中国科学:数学,2011,41(6);485-496. [23] 李长江,杨丕文. 拟四元数空间中的一些边值问题[J]. 四川师范大学学报:自然科学版,2010,33(03):286-291. [24] Yang P W, Li D.Hλ-regular vector functions and their boundary value problems[J]. Boundary Value Problems,2012,2012:75. [25] 李觉友. Moisil-Theodorsco方程组的一个非线性边值问题[J]. 重庆师范大学学报:自然科学版,2008,25(1):42-46. [26] 李觉友. 非齐次Moisil-Theodorsco方程组的Riemann边值问题[J]. 重庆师范大学学报:自然科学版,2007,24(4):27-29.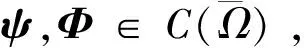
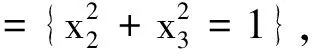
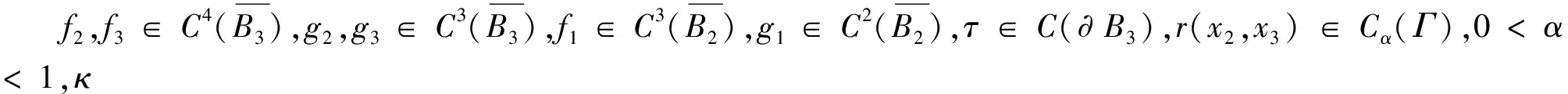


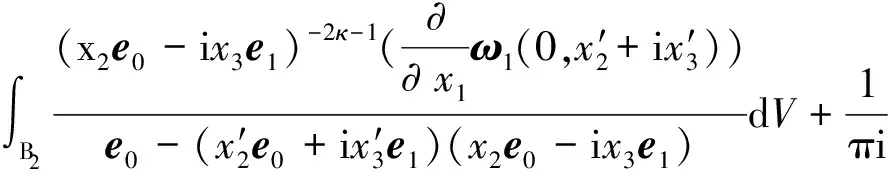
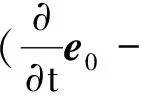
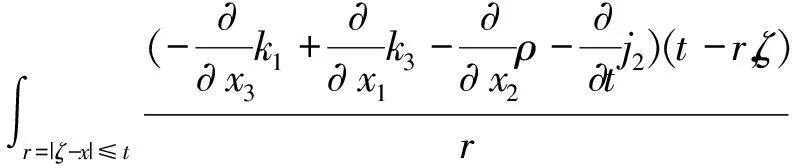
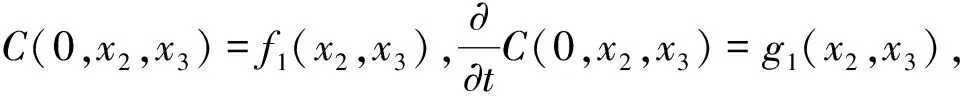
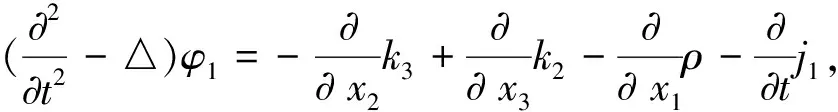
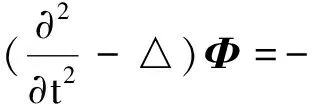
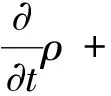
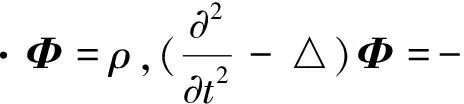

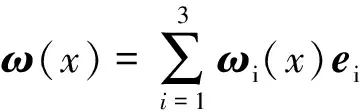
3 含磁单极子的Maxwell方程组的初边值问题