重大疾病保险的保险需求与最优免赔额的确定
田 乾, 金怀玉, 胡宏兵
(1.安徽科技学院 财经学院, 安徽 蚌埠 233100 ;2.中南财经政法大学 金融学院 湖北 武汉 430073)
一、引言
重大疾病保险,是指当被保险人在保险期间内发生保险合同约定的疾病、达到约定的疾病状态或实施了约定的手术时给付保险金的健康保险产品。
1983年,南非外科医生马里优斯巴纳德最先提出了重大疾病保险这一产品创意,我国内地市场在1995年引入了重大疾病保险,并逐渐成为人身保险市场上重要的保障型产品。[1]目前,关于重大疾病险国内的定义一般是保险公司经办的以特定重大疾病为保险对象的商业保险,但对于特定重大疾病,不同的险种有不同的定义,但可以确定的是,投保人购买重大疾病保险获得的给付保险金主要有两方面的用途:一是为被保险人支付因疾病、疾病状态或手术治疗所花费的高额医疗费用;二是为被保险人患病后提供经济保障,尽可能避免被保险人的家庭在经济上陷入困境。
随着医疗费用的上涨、大众对健康管理关注度的不断上升以及癌症等重大疾病发病率的高涨,我国健康保险市场出现了对重大疾病保险的强烈需求。然而,重大疾病风险相比较其他的健康风险而言,具有低概率、高损失(LPHL)的特性,故对于重大疾病保险的需求决策在本质上来说是不确定条件下的决策。
首先,对于重大疾病保险的需求客观存在,这一点无论是从理论上还是在实践中都是可以证明的。一方面,从理论上看,在保费精算公平的情况下,对于单一的风险而言,投保人选择最优保险需求时,选择的应该是全额保险,而非部分保险。无论是从预期效用模型(Arrow 1965)[2]还是从基于二阶随机占优的非预期效用模型(Machina 1995)[3],都能证明此结论。但是,当保费并非等于纯保费(保单精算价值),而是等于纯保费附加一个正比例的附加费用时,投保人选择的最优保险需求则是部分保险。另一方面,从现实情况看,重大疾病风险发生的概率远远小于普通疾病,但这并不是说没有必要对其进行防范,相反,每个人尤其是工薪阶层,须将重大疾病风险作为必须防范的风险,体现在家庭或个人的理财规划之中。
这是因为,尽管重大疾病风险发生的概率比较小,但一旦发生,对每个人、每个家庭带来的损失是巨大的,甚至可能使一个富有的家庭背上沉重的债务负担。[4]因而,无论是从理论分析还是实际条件分析角度看,可以肯定的一点是,重疾保险需求是实际存在的。
商业保险公司的保费不但要覆盖保险产品交易过程中的一系列费用,作为商业团体,还需要获得至少是正常的市场利润,因而,部分保险的保险需求在现实的保险市场中是最常见到的,对于重大疾病保险当然也不例外。因而,对于保险公司,到底以多大的比例承保,对于投保人,以多大的比例投保,是值得深入研究的。将重大疾病保险定义在一个更广更一般的领域,也就是LPHL风险的大领域中,可以运用多种相关模型对这一问题进行探讨。
在过去的几十年中,众多学者对个人关于风险与保护机制的决策框架进行了研究,并逐步形成了比较完善的决策框架,这些研究也包括了重大疾病风险在内的一些LPHL风险事件。根据Mc-Clelland的试验,公众对于LPHL风险主要采取两种态度:一是置之不理,即对这种风险采取放任态度,不会通过保险等方式进行分散或转移;二是支付过高,即对这种风险采取过度的方式进行分散或转移[5]。人们为什么对LPHL风险置之不理,其原因包括概率提出的背景、财富效应、过去的经验、有限理性,等等。总而言之,理论方面的研究还不能够很好地解释公众面临风险,尤其是LPHL风险时具体应该如何进行有效地决策。
在实际中,人们往往面临多种多样的健康风险,单一风险情形是不存在的。例如,健康风险引发的相关医疗费用风险除了有重大疾病的医疗费用风险(LPHL),还有发生可能性更高,但费用损失程度较低的一般住院费用风险(一般风险),本文的分析基于随机占优偏好的效用理论和预期效用理论,分析重大疾病保险最优免赔额的确定,并考虑在不完全市场中的非单一健康风险条件对重大疾病保险需求的影响。
二、重大疾病保险最优免赔额分析
(一)模型分析
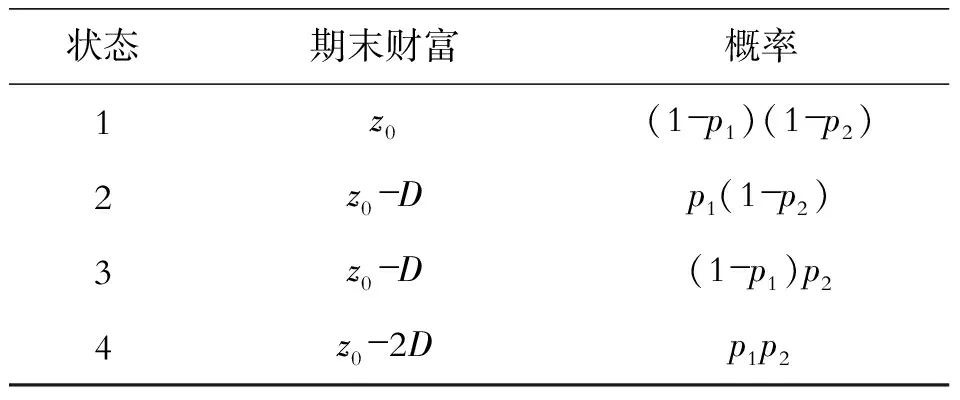
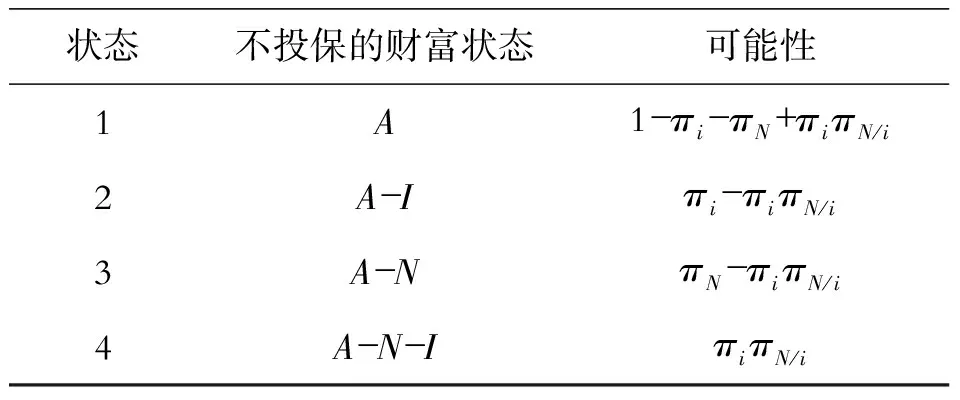
为了简化模型,假设决策者面临两种不同性质的纯粹风险,分别定义为风险x1和x2,两者发生的概率以及损失不同,并且两者是相互独立的。然后,进一步假设x1发生概率为p1,损失为L1,x2发生概率为p2,损失为L2,并且L1>L2,p1 在这种假设条件下,决策者(或称投保人)在为这两种风险进行投保时,最优的免赔金额D1和D2应各自为多少? 免赔额的高低对决策者的预期效用主要有两个方面的影响。一方面,较高的免赔额意味着较低的保费支出,可以减轻投保人投保时的经济负担;而另一方面,较高的免赔额也意味着较大的风险敞口,也就是说,一旦有损失发生,决策者从保险公司获得的赔偿将变少,决策者将不得不自己承担重大的经济损失。因此,作为理性效用最大化的决策者,其决策目标就是选择最优的免赔金额,使得这两种影响的边际效应正好互相抵消,从而获得最大的效用。 为简单起见,假设x1和x2是相互独立的①,风险i的分布为(0,1-pi,Li,pi),并且L1p1=L2p2,即两个风险的期望损失相等。保险人为这两种风险提供保险,免赔金额为Di,即若损失发生,受益人或投保人能够获得的实际赔偿金额等于扣除免赔额后的损失金额。 假设保险人的附加费用与保单精算价值成正比,且两种保险的附加系数d>1是相等的,则免赔额为Di的保险其保费计算应为: Pi(Di)=d×pi(Li-Di) 如果决策者(或称投保人)购买两种保险的免赔额分别为D1,D2,则保险合同到期时其财富为: ϖ(D1,D2)=ϖ0-L1+max(0,L1-D1)- L2+max(0,L2-D2)-P1(D1)-P2(D2) 式中,ϖ0代表的是决策者的初始(或称购买两种保险合同前)财富,P1(D1)和P2(D2)分别代表的是两种保险的保费。 因此,决策者的决策目标是在一定的保费预算限制下: maxU(ϖ(D1,D2)) 式中,U代表的是决策者的效用函数。 本文的研究中,不对效用函数作过多的限制,仅假设决策者具有二阶随机占优的偏好。 如果d≠1,最优的保险需求D1, 相对于D2,又应该为多少呢? 首先应该考虑的是D1和D2相对大小。假设存在两个保险策略,分别为(D,D)和(D1,D2),并且D1>D2,同时两个保险策略的保费预算相等。于是得出如下结论:在上述的限制性条件下,保险策略(D,D)是二阶随机优于保险策略(D1,D2)的。这是因为: 设z0=ϖ0-P1(D1)-P2(D2), 则策略(D,D)的支付如表1: 表1 策略(D,D)的支付情况 策略(D1,D2)且D1>D2的支付如表2: 表2 策略(D1,D2)的支付情况 则这两种策略期末财富的期望分别为: E(ϖ(D,D))=z0-Dp1-Dp2 E(ϖ(D1,D2))=z0-D1p1-D2p2 又因为这两种策略的保险预算是相等的,即Dp1+Dp2=D1p1+D2p2,所以,E(ϖ(D,D))=E(ϖ(D1,D2)),也就是两种策略的期末财富的期望是相等的。 简单来说,对这种风险采取放任态度的决策者(即风险中立者)而言,这两种保险策略是不存在差别的;而对这种风险采取支付过高的决策者(即风险厌恶者)而言,分析哪种策略更优,则需要对这种策略的期末财富的方差进行分析。 通过分析可以发现,在这两种保险策略下,每一种策略下的四种状态分布的概率都是相同的,但相比较第一种策略而言,第二种策略的分布状况更加离散,由此可以认为,第二种策略的方差相比较第一种策略而言,方差更大。 通过上述分析,可以得出以下结论:如果决策者(或称投保人)具有二阶随机占优偏好,他选择的保险策略是LPHL风险的免赔金额不应该大于其他一般风险的免赔金额。换言之,在同时存在重大疾病风险和一般住院风险的情况下,决策者应该选择对这两种风险同时进行投保,而不是仅仅投保一般住院风险。此外,重大疾病风险保险的免赔金额不应大于一般住院费用风险。同时得出以下的3个推理: (1)当两种风险具有相同期望损失时,任何具有二阶随机占优偏好的决策者对重大疾病风险的保险比率大于其它风险。这是因为: (2)对于保险费用而言,重大疾病风险所占的保险费用一般应大于住院风险所占的保险费用,换言之,重大疾病风险所占的保险费用应该占到总保费的1/2以上。这是因为: 上述两式相减等于: 根据前面的假设,p1L1=p2L2,则: 即在最优保险策略下,重大疾病风险的保费预算应该大于一般住院风险的保费预算。 (3)由于在最优保险策略下,购买重大疾病风险的免赔额不应该大于购买一般住院风险的免赔额,所以,如果通过购买一般住院风险的保险能够增加决策者的效用水平的话,同时购买重大疾病风险的保险则能进一步提高决策者的效用水平。 上述分析从理论上证明了,对于理性的决策者而言,其存在对重大疾病风险的保险需求,这也为我国重大疾病保险的进一步发展提供了理论基础。 以上研究是基于完全保险市场假设的,即决策者可以自行为自己所面临的健康风险决定保险策略,但事实上,保险公司实际提供的保险产品并没有覆盖所有的健康风险。例如,在我国目前的健康险市场中,小额门诊费用并不包含在一般的商业医疗保险负担范围中,由于小额门诊支出频繁,不好控制,商业保险公司对其敬而远之。这样,可以将其看成是不可保的健康风险。 简化消费者面临的健康风险状况,设消费者面临两种纯粹风险,重大疾病医疗费用风险可能损失I(风险发生概率为πi),不可保医疗费用风险可能损失N(风险发生概率为πN),决策者初始财富为A。这样,在未来,他所面临4种可能状态见表3: 表3 决策者面临的4种可能状态 保费支出P=α*πi*I(I+d)。 其中,α是可保风险的投保程度;d是附加费率。 决策者的预期效用函数为 EU=π1*U[A-α*πi*I*(1+d)]+π2*U[A-απi*I*(1+d)-I(1-α)]+π3*U[A-α*πi*I*(1+d)-N]+π4*U[A-α*πi*I*(1+d)-I(1-α)-N] 由于重大疾病保险是补偿性质的保险,所以α不可能大于1,所以只要上式是非负的,就可以认为决策者投保完全保险是最优的。 但在有附加保费的情况下,即d>0时(现实中也是如此),对于负相关的重大疾病风险和不可保健康风险,不完全投保结果仍成立,但对于两者存在正相关关系的情况下,则要考虑d的大小和两者正相关的程度。如果d很小,两者正相关的程度很大,使得πN在乘以(1+d)倍后仍小于πN/i,则完全投保是理性的,但如果d很大以至于πN在乘以(1+d)倍后大于πN/i,则不完全投保是正确选择。 以上是对与重大疾病风险有相关关系的不可保健康风险存在的现实保险市场中,重大疾病风险的保险需求的理论分析,基于的假设是决策者的期望效用函数符合递增性和凹性,决策者的目标是预期效用最大化。 在现实中,即使理性的保险需求者满足以上假设,在做健康风险管理的保险决策时,决策者也很难准确地把握重大疾病风险和其他不可保健康风险的相关性和程度,尤其是在附加费率存在的情况下。比如,虽然在现实中,直觉告诉人们平时住院较频繁的决策者患重大疾风险的可能性更大,但事实上并非如此,毕竟,有一点容易忽视,许多重大疾病的医疗费用巨大损失是由于病情没能及时发现,而住院频繁的决策者由于会接受住院期间相关健康检查,早期发现重疾风险的可能性更大。 注释: ①虽然两者很显然存在一定的相关关系,但由于在此处只是想探讨重大疾病保险最优免赔额的确定,一般医疗保险在此只用于做一个参照,因而对两者独立性的假设是可以用的。 ②预期效用函数二阶导数小于0。 ③对于损失补偿性质的保险,投保人不能购买超额保险,投保人或受益人得到的实际补偿金额不会超过发生的实际损失金额。 参考文献: [1]中国保险监督管理委员会.重大疾病保险知识问答(一)[EB/OL].(2007-07-05).http://www.circ.gov.cn/tabid/106/InfoID/48824/frtid/3871/Default.aspx. [2]Arrow,Kenneth J.Uncertainty and the Welfare Economics of Medical Care: Reply (The Implications of Transaction Costs and Adjustment Lags)[J].American Economic Review,1965(3):154-158. [3]Machina, Mark J.Non-Expected Utility and the Robustness of the Classical Insurance Paradigm[J].GENEVA Papers on Risk & Insurance-Theory,1995(6):9-50. [4]黄结平,刘海霞.我国重大疾病险存在问题与发展对策[J].保险职业学院学报,2006(5):30-32. [5]Mc Clelland G H, Schulze W D,Coursey D L. Insurance for Low-Probability Hazards: a Bimodal Response to Unlikely Events[J]. Journal of Risk andUncertainty, 1993 (7): 95-116. [6]刘朝辉,胡新辉,王慧敏.多重风险下洪水保险需求分析[J].人民长江,2008(20) :88-89. [7]Louis Eeckhoudt,Christian Gollier. The Insurance of Lower Probability Events[J]. The Journal of Risk and Insurance,1996(1):17-28. [8]Doherty,Neil A. Schlesinger,Harris. Optimal Insurance in Incomplete Markets[J]. Journal of Political Economy,1983(6):91-102. [9]Gary H.McClelland,William D. Schulze,Don L.Coursey.Insurance for low-probability hazards:A bimodal response to unlikely events[J]. Journal of Risk and Uncertainty,1993(7):95-116. [10]魏思博,马琼.天气指数农业保险探究——以河北省农村为例[J].石家庄铁道大学学报:社会科学版,2012(3):13-17.

(二)结论分析
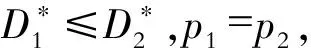
三、基于不完全保险市场的重大疾病保险的保险需求分析
(一)模型分析

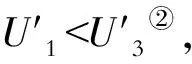
(二)结论分析
——与林刚先生商榷

