基于扩频的雷达
--通信一体化信号的设计∗
刘少华,黄志星
(电子科技大学电子科学技术研究院,四川成都611731)
0 引言
现代化战争对作战平台提出了小型化、多功能化的要求,而雷达与通信作为作战平台的两个主要组成部分,二者一体化的实现具有重要的意义。文献[1]和[2]对雷达通信一体化的必要性、可行性、关键技术及其实现方法进行了初步的分析。传统的实现雷达-通信一体化的方式有共享射频前端、共享孔径等[3],但这仅限于部分资源的共享,并非实际意义上的一体化实现。文献[4]提出了信号共享的概念,即通过发射一种信号来同时实现多种电子设备的功能,可最大限度地实现资源共享。
基于信号共享的思想,国内外学者提出了众多雷达-通信一体化的实现方案。文献[5]通过将通信信号调制到雷达信号上形成发射信号,在接收端再将雷达信号与通信信号进行分离的方法对雷达-通信一体化信号进行了设计。该方法容易因雷达信号与通信信号分离不彻底而造成二者间的干扰,并且通信信号占用大量雷达发射功率,大大降低了雷达的作用距离。文献[6]提出了一种基于Chirp信号分数阶傅里叶变换的雷达通信一体化系统,采用不同的初始频率对用户数据进行调制。但这一系统存在通信速率取决于Chirp率,以至于通信频谱效率较低的缺点。
出于扩频技术在数字通信中的广泛应用,部分学者开始以扩频技术为基础对雷达-通信一体化信号进行设计。文献[7]和[8]提出了一种基于直接序列扩频的雷达-通信一体化系统,利用PN码良好的互相关性来实现雷达信号和通信信号的正交,以在接收端将二者很好的分离。同样,该方法依旧存在通信信号占用雷达发射功率的问题,并且系统频谱利用率低,难以满足实际要求。
由此,本文设计了一种基于MSK直接序列扩频的雷达-通信一体化信号。通过对通信中的数字基带信号进行扩频,使其具有良好的自相关性,从而满足雷达探测的要求。同时,利用MSK技术,大大提升了系统的频谱利用率。
1 雷达-通信一体化信号的设计
1.1 直接序列扩频
由于具有抗干扰抗衰落能力强、功率谱密度低、可用于实现多址通信等众多优点,扩频技术已在现代通信中得到了广泛的应用,尤其以扩频技术为基础的码分多址更是显示出强大的生命力。
所谓扩频,即利用扩频序列将所传送的数据信息扩展到一个很宽的频带上,在接收端再通过相关检测以恢复出数据信息[9]。通常,以伪随机(Pseudo-Noise,PN)序列来作为扩频序列。直接序列扩频(Direct Sequence Spread Spectrum,DSSS)则是扩频通信方式中较为常用的一种,其直接将伪随机序列与数据序列相乘来实现基带信号的扩展。
基带数据序列可表示为
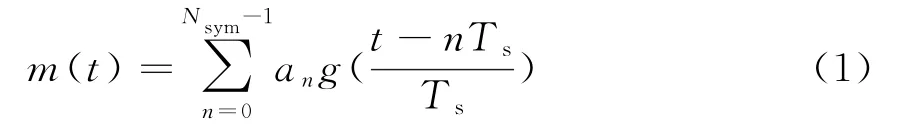
式中,Nsym为数据序列长度;Ts为码元周期;a n为所传送的第n个码元,取值为±1;则表示矩形脉冲,
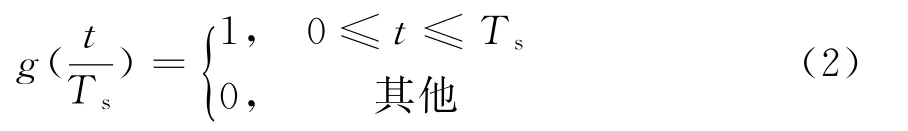
假设PN码产生器所产生的伪随机序列为
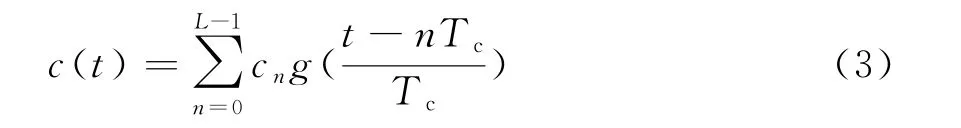
式中,L为伪随机序列长度(亦即扩频因子);Tc为PN码码元周期;c n为第n个PN码码元,取值为±1。通常情况下,伪随机序列码元宽度远远小于数据序列的码元时间间隔,即Tc=Ts。则经过扩展后的序列为
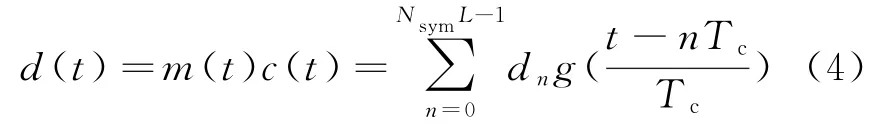
式中,d n为经过扩展后的第n个码元。这种扩展方式也称为二进制相移键控直接序列扩频系统。
然而,由于BPSK调制的固有缺陷,二进制相移键控下的DSSS系统频谱利用率将会很低,大大限制了它的实际应用。MSK(最小频移键控)作为连续相位频率调制体制中的一种,则具有较高的频谱效率。故接下来,本文将利用MSK技术来对雷达-通信一体化信号进行设计。
1 .2 MSK直接序列扩频
MSK是连续相位频率调制体制中的一种特殊类型,其具有线性、连续的相位路径。由于其消除了码元转换时刻的相位突变,从而从根本上解决了已调信号包络起伏问题,其频谱滚降也得到了显著的改善。假设MSK与QPSK信号码元周期相同,二者归一化功率谱如图1所示。

图1 MSK与QPSK信号归一化功率谱
可见,MSK信号的功率谱比QPSK具有更窄的主瓣,并且其功率谱衰减速率也远远大于QPSK的衰减速率,从而具有更高的频谱效率。
根据MSK信号形式[9],MSK直接序列扩频(MSK-DSSS)发射端在第n个码元周期内的输出信号可以表示为
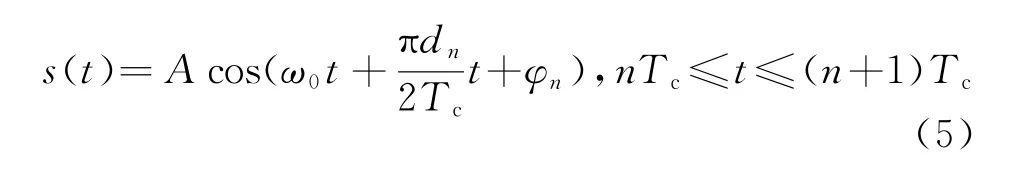
式中,A为信号幅度,简单起见取值为1;ω0为载波频率;d n为经过扩展后的第n个码元;φn为第n个码元的相位常数。为保证MSK-DSSS信号相位在码元转换时刻是连续的,φn应满足以下约束条件:
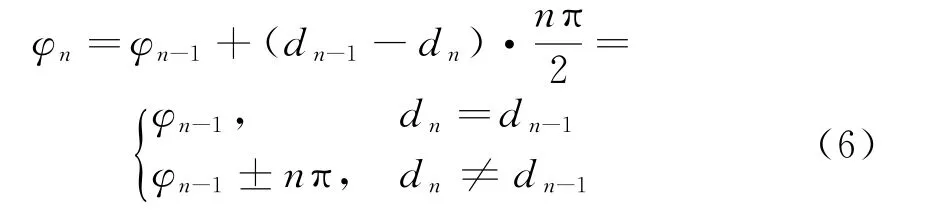
由此,可以构建出MSK直接序列扩频信号的产生框图,如图2所示。
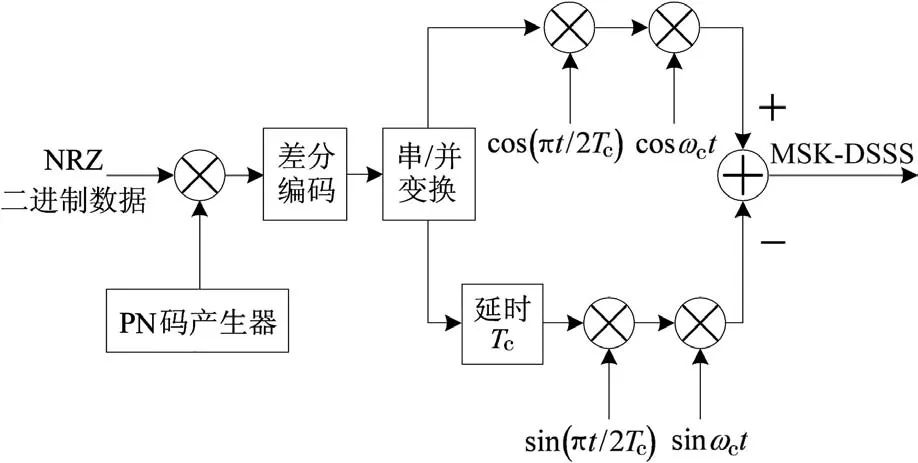
图2 MSK-DSSS信号的产生
根据式(5),MSK-DSSS基带复包络信号则可表示为
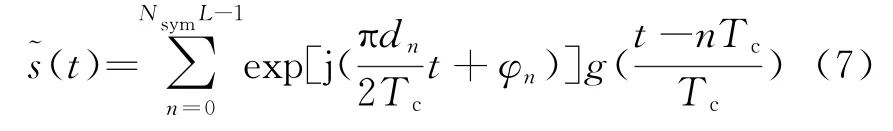
可见,该信号具有恒定的包络,这将使其免受系统中诸多非线性器件的影响。
下面,将分别对MSK-DSSS基带复包络信号的频谱及其模糊函数性能进行分析,以分析各参数对该雷达-通信一体化信号的影响。
2 频谱与模糊函数分析
2.1 频谱分析
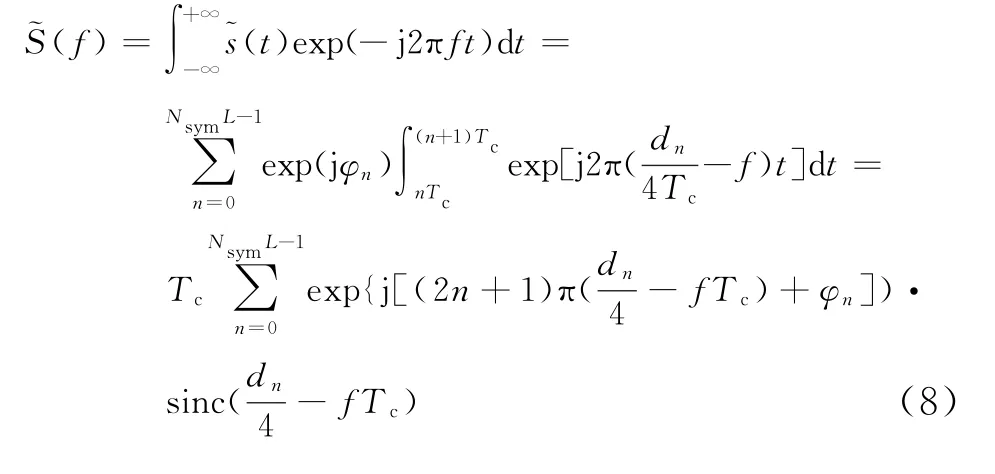
取Nsym为50,L为63,Tc为0.1μs,并令MSK-DSSS与QPSK-DSSS基带复包络信号码元周期相同,二者频谱对比如图3所示。
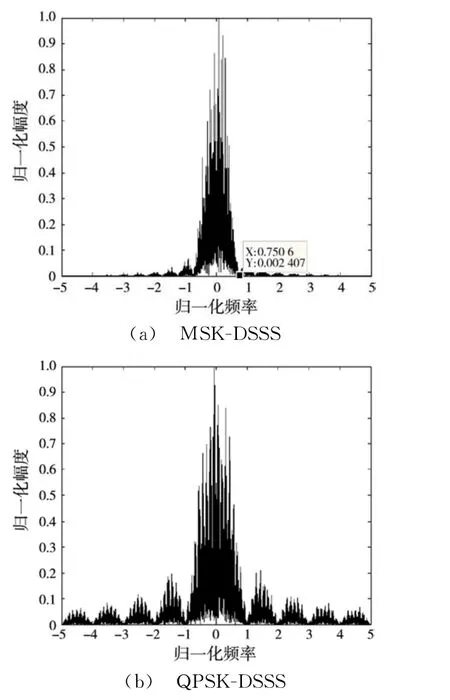
图3 MSK-DSSS与QPSK-DSSS信号频谱对比
由图3可见,MSK-DSSS基带复包络信号频谱宽度直接取决于PN码的码元周期,而与其他因素无关,并且其主瓣更窄,频谱衰减速率更快,进一步验证了MSK-DSSS系统具有更高的频谱效率。
2.2 模糊函数分析
(1)模糊函数
雷达模糊函数作为研究不同雷达波形的主要工具,其直接反映了特定波形的距离和多普勒分辨率。信号s(t)的雷达模糊函数定义为
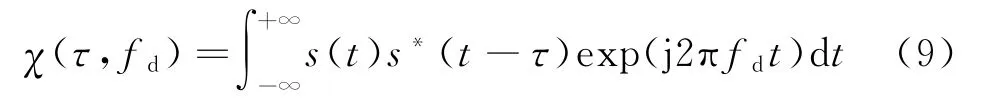
式中,τ为延时时间;fd为多普勒频移。
将式(7)代入式(9),可得MSK-DSSS信号模糊函数为
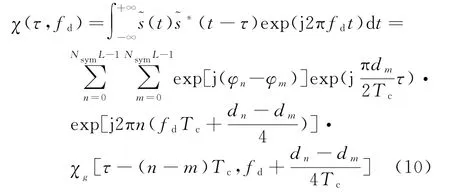
式中,χg(τ,fd)为矩形脉冲的模糊函数。通过计算,可得
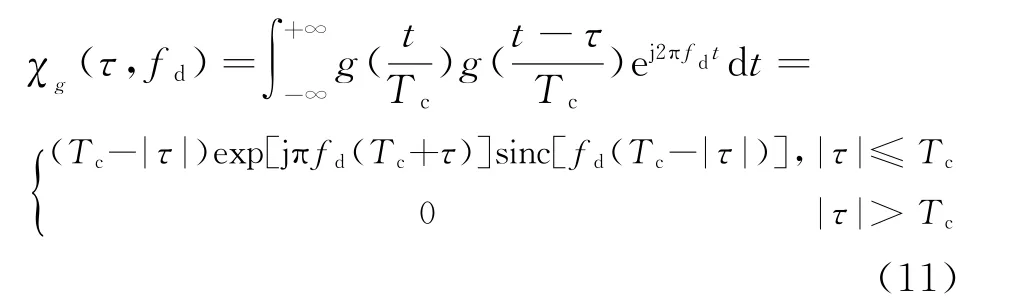
(2)距离模糊函数
在模糊函数中,令多普勒频移fd为0,可得其在时延轴τ上的切面,即距离模糊函数,
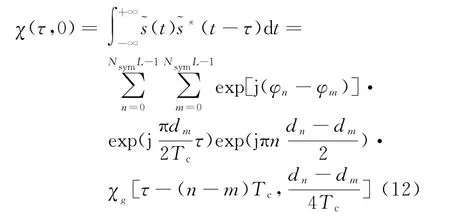
式中,χg(τ,fd)为矩形脉冲的模糊函数,如式(11)所示。
(3)速度模糊函数
与距离模糊函数的获得相似,在模糊函数中,令时延τ为0,则可得其在多普勒频率轴fd上的切面,亦即速度模糊函数,
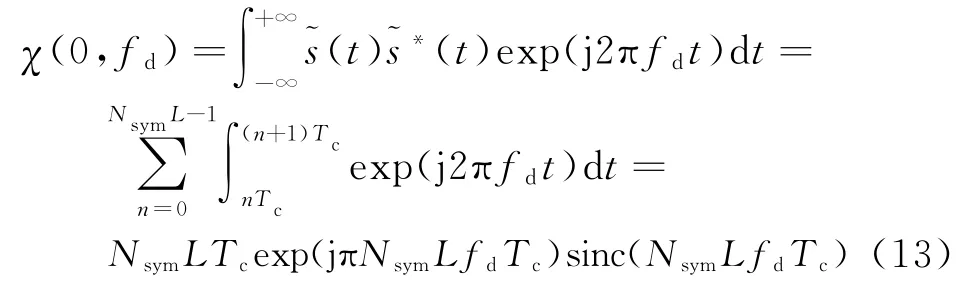
观察上式可得,MSK-DSSS信号的速度模糊函数主要取决于数据序列长度Nsym、扩频因子L以及PN码码元周期Tc。
3 仿真分析
3.1 传送数据内容对模糊函数的影响
由式(13)可知,所传送的数据内容不会对MSK-DSSS信号的速度模糊函数产生任何的影响,故在此仅对该信号在不同数据内容下的距离模糊函数进行仿真分析。令Nsym为10,L为127,Tc为0.1μs,图4给出了不同数据内容下MSK-DSSS信号的零多普勒切面。
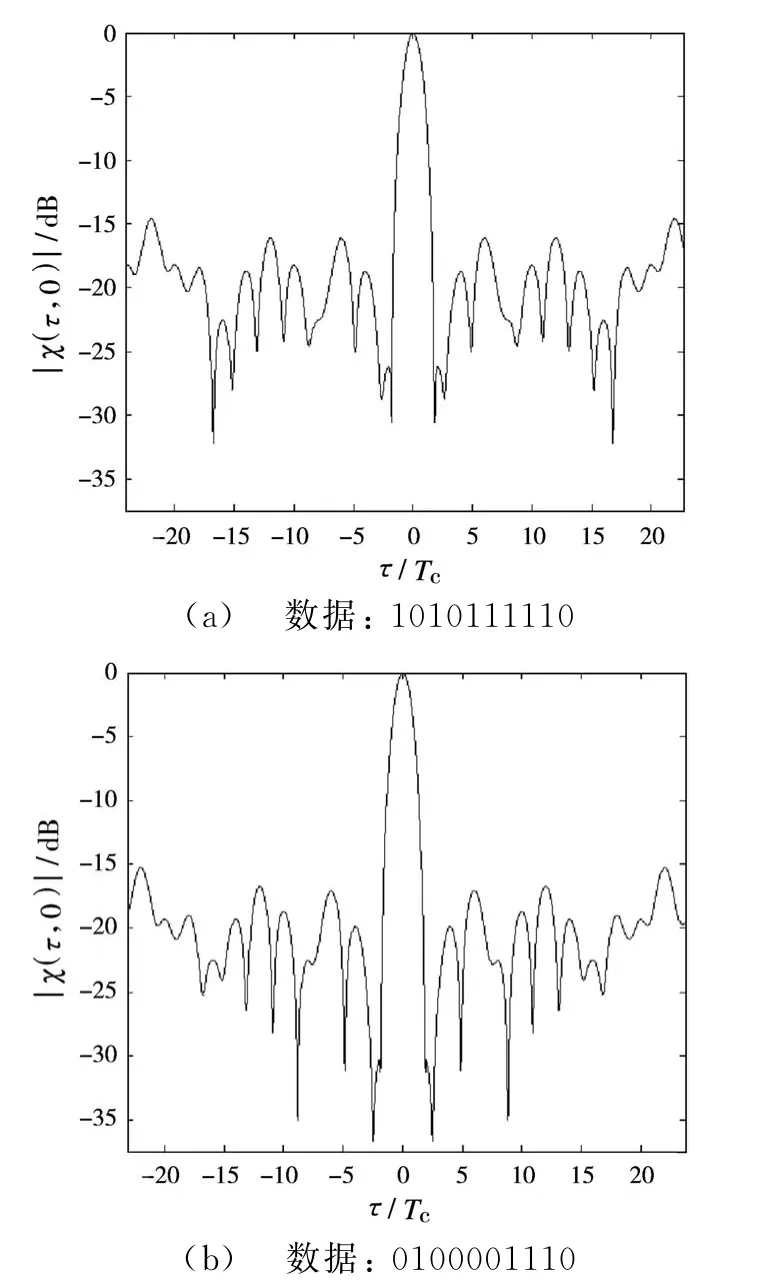
图4 不同数据内容下的零多普勒切面
由图4可以看出,所传送的数据内容几乎不会对MSK-DSSS信号的模糊函数产生任何的影响。
3.2 数据序列长度对模糊函数的影响
令L为127,Tc为0.1μs,分别对数据序列长度Nsym为10和50 MSK-DSSS信号的模糊函数进行仿真,仿真结果如图5和图6所示。
对图5和图6进行分析可知,随着数据序列长度的增加,MSK-DSSS信号的距离模糊函数几乎不受影响,而其速度模糊函数主瓣变窄,速度分辨率得到进一步提升。
3.3 扩频因子对模糊函数的影响
令Nsym为10,Tc为0.1μs,分别对扩频因子L为31和255 MSK-DSSS信号的模糊函数进行仿真,如图7和图8所示。
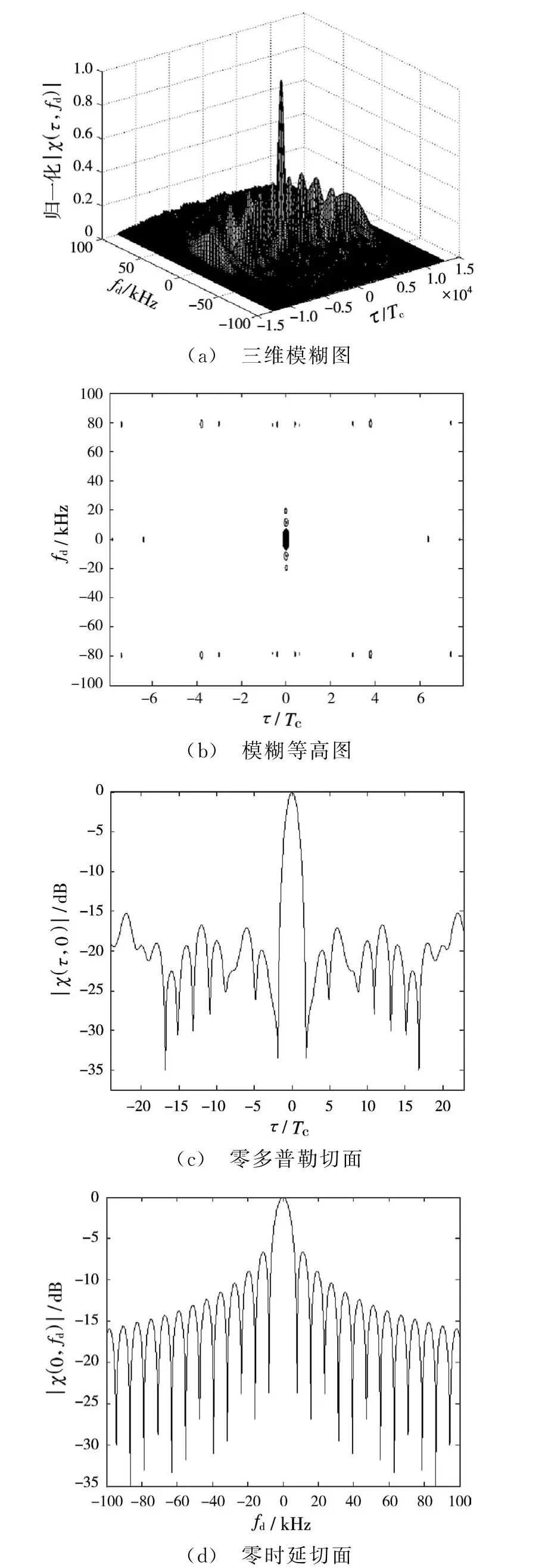
图5 数据序列长度Nsym为10的模糊函数
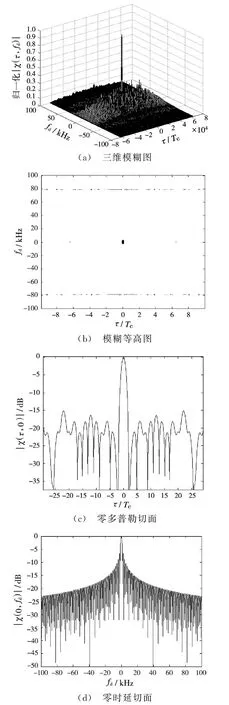
图6 数据序列长度Nsym为50的模糊函数
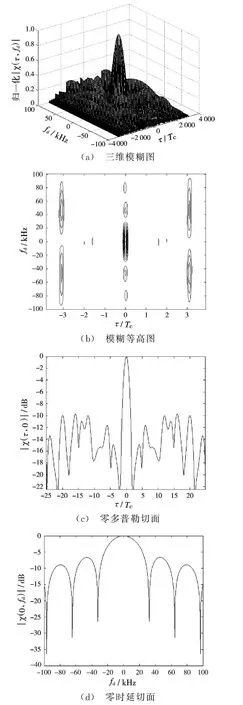
图7 扩频因子L为31的模糊函数
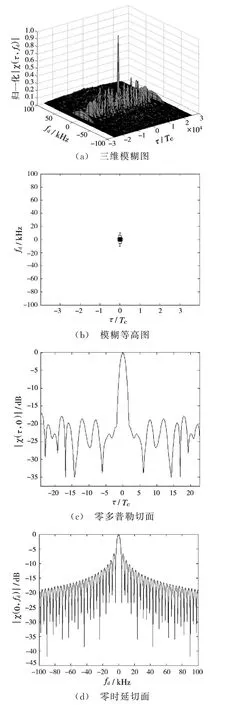
图8 扩频因子L为255的模糊函数
可见,随着扩频因子的增大,MSK-DSSS信号的距离模糊函数旁瓣降低,距离分辨率得以提升。同时,其速度模糊函数的主瓣也变得更窄,速度分辨率也得到进一步提升。
4 结束语
本文基于MSK直接序列扩频技术,对雷达-通信一体化信号进行了设计,并分别从频谱以及模糊函数的角度对其作了详细的分析。该信号具有恒定的包络、较高的频谱效率、较强的抗干扰和抗衰落能力以及可用于实现多址通信等优点。
由于雷达-通信一体化工程在国内尚处于起步阶段,故仍有众多关键问题还需作进一步研究,如一体化系统工作方式的设定,一体通信协议的制定等。
[1]张明友.雷达电子战-通信一体化概论[M].北京:国防工业出版社,2010:94-98.
[2]林志远,刘刚.雷达-电子战-通信的一体化[J].上海航天,2004(6):55-58.
[3]Tavik G C,Hilterbrick C L,Evins J B,et al.The Advanced Multifunction RF Concept[J].IEEE Trans on Microwave Theory and Techniques,2005,53(3):1009-1020.
[4]Xu Cuichun,Chen Tianqi.Conception of Signal Sharing in Integrated Radar and Jammer System and the Integrated Signal Design[C]∥The 2002 IEEE International Conference on Communications,Circuits and Systems,[s.l.]:IEEE,2002:502-505.
[5]邹广超,刘以安,吴少鹏,等.雷达-通信一体化系统设计[J].计算机仿真,2011,28(8):1-4.
[6]李晓柏,杨瑞娟,程伟.基于Chirp信号的雷达通信一体化研究[J].雷达科学与技术,2012,10(2):180-186.LI Xiao-bai,YANG Rui-juan,CHENG Wei.Integrated Radar and Communication Based on Chirp[J].Radar Science and Technology,2012,10(2):180-186.(in Chinese)
[7]Xu S J,Chen Y,Zhang P.Integrated Radar and Communication Based on DS-UWB[C]∥The Third International Conference Ultrawideband and Ultrashort Impulse Signals,Sevastopol,UK:[s.n.],2006:142-144.
[8]Xu Shaojian,Chen Bing,Zhang Ping.Radar-Communication Integration Based on DSSS Techniques[C]∥2006 8th International Conference on Signal Processing,Beijing,China:[s.n.],2006:16-20.
[9]王军选,张晓燕,张燕燕.无线通信调制与编码[M].北京:人民邮电出版社,2008:13-17.

