高频地波雷达系统优化控制的研究与建模∗

陈文涛,马子龙,周必全

(哈尔滨工业大学(威海)信息与电气工程学院,山东威海264209)

0 引言

高频地波雷达利用垂直极化电磁波沿地球表面绕射的原理,可以探测到视距以外的低空飞机、舰船和巡航导弹等目标,并且可以从海面后向散射回波中提取洋流、海面风场的速度和方向以及浪高等各种海态信息。由于高频地波雷达系统是复杂、非线性的系统,同时,系统模型中一部分变量的数学模型无法建立或者系统中可能部分模糊变量,所以常规的控制方法无法应用到雷达系统中。

模糊控制作为智能控制的重要分支于1965年由Zadeh提出[1]。模糊控制模拟人类思想,设计简单,鲁棒性高,适合非线性、复杂系统。模糊控制还具有一定的抗干扰和解耦合能力,且不需要系统的数学模型。所以模糊控制在智能控制工程中取得广泛应用。

本文在高频地波雷达仿真系统中通过模糊控制方法控制发射信号的功率、频率和相参积累时间等参数的设定,产生合适发射信号波形参数,使雷达达到期望的工作性能。利用基于遗产算法的模糊控制算法和基于粒子群优化算法的模糊控制器解决了模糊控制器参数设定的困难。根据高频地波雷达仿真系统的特点提出了基于粒子群改进算法的模糊控制器提高了控制精度和运算时间,设计实现了基于Matlab的雷达控制软件。

1 高频地波雷达仿真系统

1.1 高频地波雷达目标回波功率

本文根据高频地波雷达方程建立目标回波功率模型。根据高频地波雷达的特性和普通雷达方程,得到单基地高频地波雷达方程。目标回波功率为

式中,E(R)为在单位雷达发射功率P0与标准天线增益D0条件下距离发射站R处的场强值;Pt为实际发射功率;γ为信号占空比;Dt为发射天线的方向性系数;Dr为接收天线的方向性系数;λ为发射信号的波长;σ为目标的有效散射面积(RCS);Ls为系统损耗;Lw为地波传播粗糙海面附加损耗;Lh为均匀光滑球形的地面衰减。

复杂系统E(R)通过程序调用GRWAVE程序计算。而简易模型为了缩短计算时间,利用插值法计算,不考虑海态的影响。虽然简单模型较复杂模型减少了系统参数,但基本符合实际系统同时计算时间大大减小。

1.2 环境噪声模型

工程中一般利用噪声系数Fa定义随机噪声系数:

式中,Pn为接收机接收噪声功率;B为接收机带宽;T0为环境绝对温度;k0为玻耳兹曼常数。

由此可以得出噪声的功率谱密度为

在复杂模型中根据ITU-RP372-6报告及利用NOIS1程序可以估算高频地波雷达的环境噪声系数,考虑的参数有频率、季节、时间、经纬度和雷达所在区域类型等参数。而在简易模型中只考虑频率的影响,附加利用实验数据观测的噪声基底。

1.3 海杂波模型

根据Barrick海浪散射理论研究,满足一定条件时,海浪和电磁波会发生共振散射,就是Bragg谐振。本文根据一阶、二阶海浪散射系数模型建立海杂波模型。参考目标的回波功率方程,海杂波的回波功率如下[2]:

与目标的回波功率模型相比只有散射面积的不同[3]:

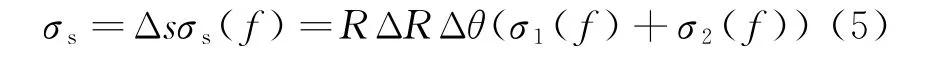
式中,Δs为雷达分辨单元;σs(f)为单位面积,单位频率海浪散射截面积;R为目标与雷达的距离;ΔR为雷达距离分辨率;Δθ为雷达角度分辨率;σ1(f)为单位面积单位频率海浪一阶散射截面积;σ2(f)为单位面积单位频率海浪二阶散射截面积。

1.4 回波信噪比模型

本文根据高频雷达系统的特点和应用范围建立了复杂和简易两套系统,其中复杂系统的目标回波功率、环境噪声和海杂波在前面已经建立,考虑目标的类型,当目标为海上舰船时,虽然通过频监系统可以避开海杂波的一阶谱峰,但海杂波中二阶谱的带宽较宽,目标速度较慢,目标的多普勒频移落在海杂波谱的范围内,所以目标的回波信噪比SNRs的定义如下:

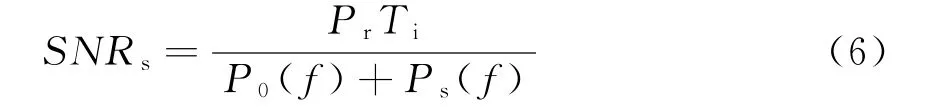
式中,Pr为目标回波功率;Ti为雷达信号相参积累时间;P0(f)为环境噪声功率谱密度;Ps(f)为海杂波功率谱密度。

当目标为海上飞机或导弹时,由于目标速度很快,目标的多普勒频移处的海杂波功率谱密度远远小于环境噪声的功率谱密度,所以目标的回波信噪比模型不考虑海杂波的影响。

简易模型中不考虑目标类型和海杂波的影响,加入了实测数据的噪声基底N,所以目标的回波信噪比为

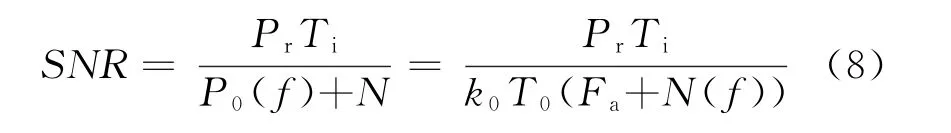
图1为两系统的回波信噪比与距离的关系。从图中看出:两套系统在相同的仿真条件下目标的回波信噪比相近,目标信噪比随着雷达距离的增加而降低,简易模型和复杂模型都可以反映高频地波雷达目标回波信噪比的特性,复杂模型考虑参数更全面,但因需要调用两次外部程序,速度较慢,不适合大量循环计算寻优,所以将简易模型作为优化模糊控制参数时的仿真平台,而复杂系统作为系统优化控制的实验平台。大量实验表明,将回波信噪比取14 dB作为检测门限、目标发现概率取为0.9是一个较合理的指标数值,所以,本文将回波信噪比为14 dB作为临界值(检测门限)来计算高频地波雷达的最大作用范围。

图1 模型波回波信噪比

2 高频地波雷达系统优化控制

高频地波雷达系统复杂、非线性和大延迟性给系统的优化控制带来了困难。同时,需要要求控制系统对外界输入的参数实时更改系统参数。模糊控制作为智能控制中的一种重要分支,是以模糊数学集合论、模糊语义变量、模糊控制规则和模糊逻辑推理为基础的高级控制策略。模糊控制的对象符合智能控制的特点,包括系统的模型的不确定性、复杂性、非线性和功能要求的多样性。因此,考虑高频地波雷达系统的特点,采用模糊控制及其改进算法对雷达系统进行优化控制。通过实时控制雷达发射功率、发射信号的频率和信号相参积累时间调节回波信噪比。

2.1 高频地波雷达模糊控制

模糊控制通过模糊推理将人的思维判断简化成数学形式,将工作经验转化成模糊控制规则,通过一系列不精确的控制达到复杂、非线性系统的精确控制[4]。模糊控制系统组成类似于一般的数字控制系统[5],如图2所示。

模糊控制算法分以下步骤:

(1)从传感器得到输入量e;

(2)通过输入量e计算误差模糊量和误差变化率的模糊量;

(3)在模糊控制规则的指导下,输出模糊控制量;

(4)非模糊化处理得到控制量的精确值。

对输入量误差E、误差变化量EC和输出量U的模糊子群采用常规7状态定义,即{正大(PB),正中(PM),正小(PS),零(O),负小(NS),负中(NM),负大(NB)},输入变量E和EC的论域为[-6,6],输出变量U的论域为[-7,7]。表1为模糊控制的规则表,图3分别是E、EC和U的隶属度函数。

表1 模糊规则控制表

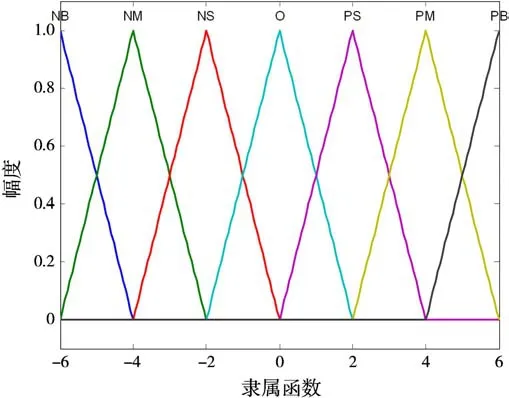
图3 隶属度函数

仿真中输入量为回波信号信噪比与目标值的误差和误差变化率,输出为雷达发射功率的控制量。量化因子K e=10,K c=8,比例因子K u=0.001。图4分别利用常规模糊控制高频地波雷达复杂系统、简易系统的仿真。

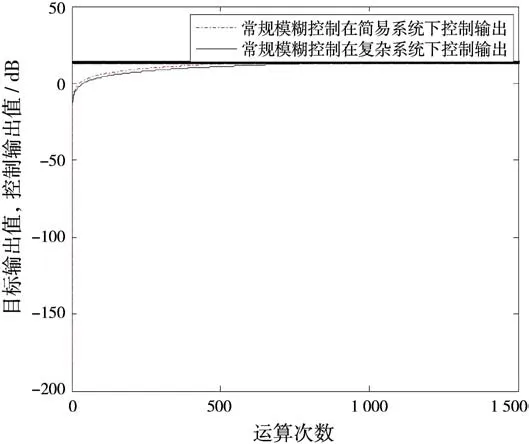
图4 模糊控制输出曲线

2.2 基于遗传算法的模糊优化控制

常规模糊控制器参数的设定依赖于大量的工作经验,将优化算法和模糊控制算法结合,利用优化算法优化模糊控制的参数,使模糊控制器正常工作,简化了参数设定的难度。

遗传算法是基于自然群体进化选择的优化算法,采用数学模型模拟自然进化的方法对目标进行优化选择。算法利用编码方式模拟成个体的染色体,反复经过算法模拟出的遗传、交叉、变异和自然选择过程,根据对每个个体的适应度的比较,获取群体中适应度的最优值,利用不断的更新群体中的个体,向最优值方向不断进化,达到优化选择的目的[6]。

基于遗传算法的模糊控制实际上是利用遗传算法优化常规模糊控制的控制参数利用5位二进制分别对12个隶属函数节点编码。精度达到0.1,三位二进数分别表示49个模糊规则编码,即每个个体为长度为207位二进制数。基于遗传算法的模糊控制算法中适应度的定义如式(9)所示。

其中e为被控系统输出与目标值的误差,如果出现超调值大于0.5,适应度为0。仿真中种群规模N=100,交叉概率Pc=0.8,变异概率Pm=0.01,进化次数为500。仿真选取的最优个体结果如图5所示。

基于高频地波雷达仿真系统,利用遗传算法实现了优化模糊控制参数,定义适应度函数为1/∫|e|dt,考虑了模糊控制算法在收敛速度、精度和振荡性三个方面的要求,同时特别考虑了防止超过0.5的超调。所以利用遗传算法优化模糊控制的参数后,模糊控制的收敛性大大增加,适应度为0.812 67,仿真中24次控制后误差小于0.1,由于遗传算法在适应度的定义上并没有特别考虑振荡和算法精度的问题,所以仿真中优化后模糊控制算法出现了轻微的超调和振荡。

图5 基于遗传算法的模糊控制输出曲线

2.3 基于粒子群算法的模糊优化控制

粒子群优化算法(PSO)[7]是基于群体协作随机搜索的优化算法,通过模拟鸟类群体觅食行为而提出的智能随机优化算法。算法在每一迭代运算中利用群体和个体最优值的信息更新个体的位置,不断地向最优值靠近。算法利用上次的速度、向个体当前最优值运动的速度和向群体当前最优值运动的速度合成个体当前速度,更新个体的位置,使群体所有的个体向最优值靠近,达到计算出最优值的目的[8]。所以速度和位置的更新方程为

粒子群优化模糊控制参数需要初始化的隶属函数节点和模糊规则的个数同基于遗传算法的模糊控制算法相同,所以需要初始化的模糊控制隶属函数节点有12个,模糊控制规则为49条。由于是两输入单输出的模糊控制器,所以需要初始化的量化因子为2个,比例因子为1个。总共维数和个体需要初始化的参数的个数为n=64。

隶属函数节点范围为[-6,6],所以产生隶属函数节点的方法为

并通过排序后初始化隶属函数节点。

模糊控制规则为1～7的正整数,利用取随机整数的函数randint(·),所以模糊规则的初始化如下:

量化因子的初始化方法为取0～50之间的随机值,比例系数为0～0.1之间的随机值。

适应度与基于遗传算法的模糊控制算法定义相同,仿真中种群规模N=20,上次速度的相对权重w=0.729 8,向当前个体最优值运动速度的相对权重c1=1.496 2,向当前种群最优值运动速度的相对权重c2=1.4962,进化次数为50。图6为基于粒子群优化法的模糊控制输出曲线。

图6 基于粒子群优化法的模糊控制输出曲线

2.4 基于优化粒子群算法的模糊优化控制

将适应度的值代入速度公式,同时为了加大种群的多样性,利用合成目标极值代替式中个体当前最优值。合成极值公式和速度更新公式为[9-10]

式中,fitness()为个体的适应度函数。

新算法在加大种群的多样性的同时,加强了个体间的信息的交流。个体能利用更多的群体信息更新位置,同时,加大了群体中个体的交流和竞争。高频地波雷达仿真程序的计算时间较长,所以粒子群改进算法种群规模和迭代次数需要限定。同时,由于一般优化算法只是将误差绝对值积分作为适应度,并不能考虑精度、振荡和超调问题。本文设定超调超过0.1适应度为0,防止了算法出现较大的超调,将适应度定义为

式中,α为收敛相对权重;β为精度相对权重;γ为振荡相对权重;σ2(N1,N2)为N1次控制至N2次控制输出的方差;y(N2)为N2次控制后输出。

收敛相对权重和精度相对权重为常数,振荡的相对权重受输出影响,当输出误差超出指定范围时适应度值变为0。本文基于雁群启示和自然进化思想改进粒子群算法,达到计算速度和优化精度的平衡。基于雁群启示的粒子群算法加大了的群体多样性,同时并没有增加多余的适应度计算,与常规粒子群优化算法相比,计算量增加不多,但这种改进牺牲了收敛速度,并不能减少迭代次数。无法减少计算量。本文将变异因子和交换因子代入算法中,一方面,变异因子和交换因子在迭代前期时,提高群体的多样性,提高搜索速度;另一方面,在迭代后期,群体趋近于最优值,不同维与最优值的误差不同,大量实验表明,优化算法计算出的多维空间的优化值与最优值只是在其中几维空间存在不同,所以,利用变异因子和交换因子提高了群体的多样性,提高了精度。变异因子的变异概率和交换因子的交换概率可以随着迭代次数线性增大,在算法初期,保证收敛速度,在算法后期,增大群体的多样性,保证算法精度。图7为基于改进算法粒子群优化算法的模糊控制的输出曲线,图8为基于改进算法和适应度的粒子群优化算法的模糊控制的输出曲线。

图7 基于粒子群改进算法的模糊控制输出曲线

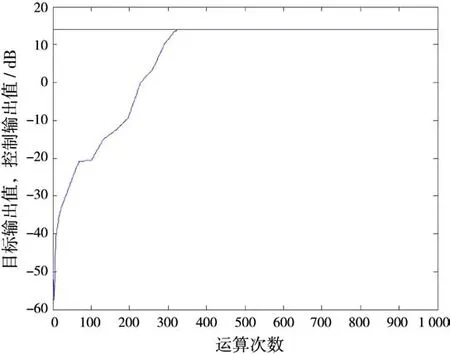
图8 基于改进算法和适应度的粒子群优化算法的模糊控制输出曲线

新算法中α=1,β=100,γ=10,N1=950,N2=1000,交叉概率Pc=0.8,变异概率Pm=0.01。使选出来的最佳参数在收敛性、误差和振荡三个方面达到平衡,从仿真图中,输出曲线误差为0.063 4,图8由于改进了适应度的计算,使在不基本影响收敛速度的条件下,减小了算法的振荡性,由于收敛速度快,不可避免地出现超调,但超调范围受适应度函数的限制,符合要求。表2和表3为常规模糊控制算法(FLC)、基于遗传算法(FLC_GA)、基于粒子群(FLC_PSO)、基于改进算法和适应度的粒子群(FLC_PSO_1)的模糊控制算法的性能比较。

表2 不同模糊控制算法的性能比较1

表3 不同模糊控制算法的性能比较2

改进算法的优点在于符合高频地波雷达系统控制的特点:

(1)相对于常规模糊控制需要设定大量的参数,利用基于改进算法和适应度的粒子群的模糊控制算法(FLC_PSO_1)对模糊控制器参数寻优,减少了设定模糊控制器参数的难度。

(2)由于实际被控系统的计算时间较长,控制次数越少,控制的时间也会较少。而改进的粒子群算法的种群规模20和迭代次数50远远小于遗传算法的种群规模100和迭代次数500,所以,优化速度优于遗传算法。

(3)改进算法综合考虑收敛性、减少振荡和减少超调等因素,改进了适应度的计算。相对于普通粒子群算法,减少了振荡和超调。

(4)算法将变异因子和交叉因子代入线性惯性因子的基于雁群启示的粒子群算法中,增加了粒子的多样性,随着计算次数的增加,粒子群的多样性增加,提高了优化精度,减少了局部收敛。

2.5 GUI软件界面

将高频地波雷达复杂仿真系统作为实验平台,设计基于Matlab的GUI界面。输入目标指标参数(最大作用距离、定位精度等),经过模糊控制输出计算出的雷达工作参数和波形参数。同时可以设置仿真环境参数和模糊控制方法,并且可以提供雷达在计算参数和波形参数下的工作性能和性能评估。软件界面如图9所示。

3 结束语

根据高频地波雷达方程、目标特点和应用特点建立两套仿真系统,为系统设计、参数优化和性能评估提供一个有效平台。采用模糊控制器对雷达系统参数进行控制,能有效实时控制雷达的工作性能。采用遗传算法和粒子群算法可以有效地优化模糊控制器,提高模糊控制器的性能。根据高频地波雷达仿真系统的特点提出的粒子群改进算法,能够提高了优化精度,减少运算时间。设计实现了基于Matlab的雷达控制软件HFR_control,为实际雷达工作参数的设定提供了指导。

图9 高频地波雷达控制界面

[1]Zadeh L A.Fuzzy Sets[J].Information and Control,1965,8(3):338-353.

[2]董英凝,张宁.高频地波雷达系统性能仿真软件的设计与实现[J].现代雷达,2009,31(10):30-34.

[3]仇永斌.双基地高频地波雷达海杂波特性研究[D].哈尔滨:哈尔滨工业大学,2011:23-26.

[4]Gao D,Wang Q,Lu D.Fuzzy Direct Adaptive Control for Robotic Manipulators[C]∥Control Automation Robotics&Vision[s.l.]:[s.n.],2010:2048-2053.

[5]Cai K Y,Zhang L.Fuzzy Reasoning as a Control Problem[J].IEEE Trans on Fuzzy Systems,2008,16(3):600-614.

[6]戴文娟,胡进峰,肖赛军,等.基于遗传算法的OTHR机动弱目标检测[J].雷达科学与技术,2013,11(1):59-64.DAI Wen-juan,HU Jin-feng,XIAO Sai-jun,et al.Maneuvering Weak Target Detection Based on Genetic Algorithm for OTH Radar[J].Radar Science and Technology,2013,11(1):59-64.(in Chinese)

[7]Dai J.Fuzzy Logic Based Control and Simulation Analysis for Nonlinear Structure[C]∥Computer Modeling and Simulation,[s.l.]:[s.n.],2010:447-451.

[8]汤可宗.遗传算法与粒子群优化算法的改进及应用研究[D].南京:南京理工大学,2011:24-43.

[9]Abdullah S,Lailee S,Hussin N M,et al.Comparative Study of Random-PSO and Linear-PSO Algorithms[C]∥Computer&Information Science(ICCIS),Kuala Lumpeu:[s.n.],2012:409-413.

[10]刘金洋.粒子群优化算法的研究与改进[D].哈尔滨:哈尔滨工业大学,2006:25-45.