穿墙雷达中的一种多层墙体强度补偿方法∗
李志希,孔令讲,贾 勇,赵中兴
(电子科技大学电子工程学院,四川成都611731)
0 引言
穿墙雷达成像由于其在反恐侦察、抗灾救援等方面的重要应用,近年来逐渐成为一个新兴的研究领域[1]。穿墙雷达成像技术主要包含两个研究方向,即穿墙人体目标成像[2-3]和建筑布局成像[4-6]。
建筑布局成像因其包含诸多好处近段时间逐步成为一个研究热点。首先,建筑布局可以作为确定穿墙目标相对位置的重要参照物;其次,建筑布局一旦确定,便能为多径的提取和目标位置偏移的纠正提供可能性;最后,建筑布局的确立为操作人员进入建筑物内部提供便利。目前,世界上存在若干研究机构就建筑布局成像进行研究[7-8]。美国陆军实验室对一简单的实际应用场景采用两视角成像融合获得了一幅粗略的全景图像。其中,每幅单视角图像的获得是在单视角下两通道图像简单相加而来,而各个单通道图像是利用合成孔径方式采用后向投影成像算法(Back Projected Algorithm)获得[9-10]。然而,电磁波信号穿墙传播引起的信号强度衰减现象带来多层墙体成像强度的非均匀,这为最终建筑布局的检测和获得带来了较大的困难。
为补偿多层墙体成像强度的衰减,本文提出了一种基于霍夫变换门限检测的补偿方法。首先,对预处理后的实测数据采用后向投影成像算法,并用PCA和模糊逻辑图像增强方法[11]处理,并产生原始图像。其次,基于固定门限值划分目标墙体区域和非目标杂波区域,门限值的确定采用本文提出的基于霍夫变换直线检测原理的处理算法,并提出数据连通域的概念。再次,获得各个目标连通域内图像像素强度的最大值并就此得到相应的强度补偿率。最后,将各个目标连通域内图像的像素统一乘上相应的强度补偿率,如此便完成了多层墙体成像衰减的补偿,能大大提高后续多视角融合后全景图像的成像质量。
1 成像模型建立
收发器平行x轴,置于x-y平面。成像区域可以被理解成M×N数据平面(m=1,2,3,…,M和n=1,2,3,…,N),如图1所示。
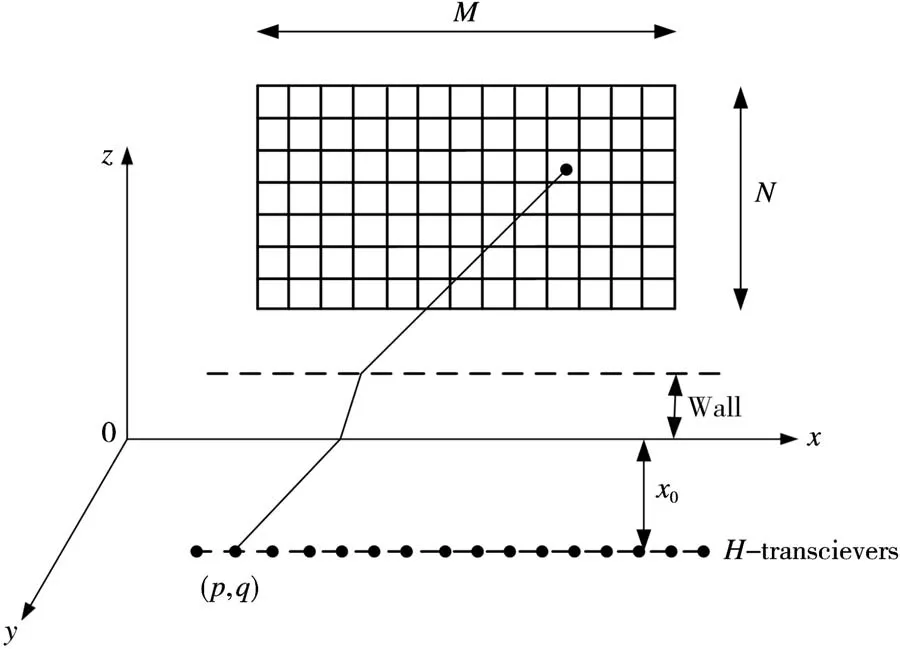
图1 回波模型建立
假设θ(t)为雷达宽带传输信号,那么成像区域位于位置(m,n)的像素值可以用信号的传播时延来表示。在x-z数据平面上位于坐标(m,n)目标值ζmn(t)在雷达坐标(p,q)可以表示为
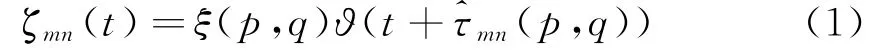
式中,ξ(p,q)为窗函数(通常是汉明窗),用来抑制旁瓣;τmn(p,q)为时域时延补偿。回波信号ϑ(t)是发射信号的时延乘以传播过程中的衰减系数αmn(p,q),即ϑmn(t)=αmn(p,q)θ(t-τmn(p,q))。令θ(t)=θ(-t),表示与发射信号匹配的滤波器,那么f mn可表示为
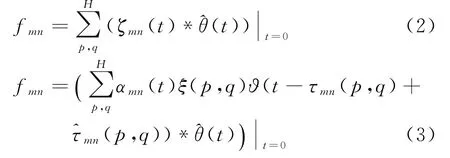
其中的时延补偿τmn(p,q)在已知墙体参数的情况下,可以用固定时延算法、最短距离算法或速度补偿算法估计[11]。经过上述处理,可以得出区域的成像:

如此得到的F便是原始输入图像矩阵。
2 算法描述
为产生一幅全景布局图像,现阶段一般采用多视角图像融合的方法。每一幅单视角图像采用后向投影成像算法获得,为改善单视角图像质量,抑制杂波,这里采用文献[11]中提到的基于PCA和模糊逻辑图像增强方法预处理图像。但由信号穿墙传播衰减引起的多层墙体成像强度的非均匀现象为最终建筑布局的检测和成像带来较大影响。对此,为补偿多层墙体衰减的非均匀现象,本文提出一种基于霍夫变换门限检测的补偿方法。由于多视角融合算法不是本文讨论的重点,不失一般性,这里仅以一幅单视角图像为例进行讨论。假设雷达在单视角下得到的图像为{F(x,y)},按幅度归一化为{I(x,y)}。本文提出的算法包括两个阶段,即检测阶段和补偿阶段。在检测阶段,算法需要划分目标墙体区域和非目标杂波区域,假设目标墙体区域设为1,非目标杂波区域设为0,那么图像{B(x,y)}可以表示为
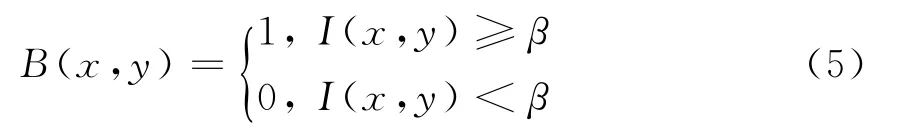
此时,问题的关键转变为如何确立固定门限β,并依此大致划分目标墙体区域和非目标杂波区域。对此本文给出一种基于霍夫变换的门限检测方法。
2.1 墙体目标检测阶段
在此阶段,需要完成固定门限检测,依此划分出目标墙体区域和非目标杂波区域,因此固定门限的选择成为了关键。由于多层墙体图像强度的非均匀,若门限选取过大,则不同墙体无法全部通过门限检测,出现“漏检”;若门限选取过小,则部分杂波可能超过检测门限,出现大量“虚警”。结合墙体图像的线性特性,本文提出一种基于霍夫变换的固定门限检测方法。
为方便说明,这里先介绍霍夫变换的相关概念。在图像处理中,霍夫变换是图像中识别几何形状的基本方法之一,有广泛的应用,也有很多改进算法。最基本的霍夫变换是从二值图像中检测直线(线段)。
如图2所示,经过霍夫变换,图像空间中的每个点(x,y)就被映射为一个(r,θ)空间中的正弦曲线。而图像空间中共线的点所对应(r,θ)空间中正弦曲线的交点(r′,θ′)。
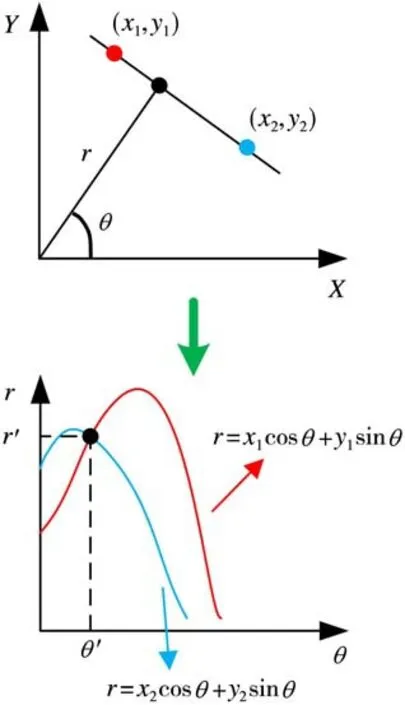
图2 运用霍夫变换直线检测
于是把在图像空间中检测直线的问题转化为在极坐标参数空间中寻找通过点(r,θ)的最多的正弦曲线数的问题。
在穿墙实际场景成像中,目标墙体在图像上近似反映为一系列线段,在图像上便可用霍夫变换检测之。但是由于杂波噪声的存在,在BP成像后的原始图像中,墙体有可能被噪声和杂波淹没,对后续的墙体检测带来困难。针对此情况,这里采用文献[11]中提到的基于PCA和模糊逻辑图像增强方法对原始图像进行预处理,便于后续的固定门限检测。一般情况下,天线合成孔径路线平行于墙体,且不同墙体之间相互平行,在图像中反映为平行于X轴的若干条矩形图案,而矩形可以表征为一系列线段的总和。于是图像中的目标墙体检测问题可以转化为直线检测问题。由于合成孔径路线平行墙体,且不同墙体相互平行,这在图像中反映为若干条平行于横轴的线段。此时倾角θ=90°,于是有
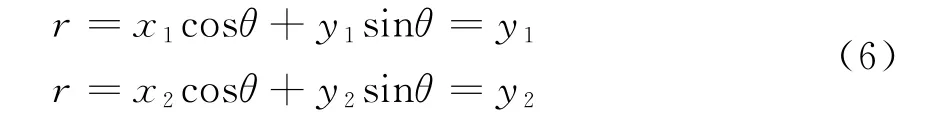
容易知道,理论上,只需对极坐标平面上θ轴坐标为90°附近的点进行反霍夫变换,便能得到不同墙体的真实目标位置。
为了确定合适的门限值,以正确划分目标墙体区域和非目标杂波区域,本文提出基于霍夫变换直线检测的门限搜索方法。首先,将区间[βmin,βmax]均匀分成若干等分,βmin代表图像像素点的像素最小值,βmax代表用Ostu自动门限阈值分割方法获得的门限值。若以βmin为门限,则所有墙体和杂波能通过门限,产生大量“虚警”;若以βmax为门限,则只有部分墙体能通过门限,产生“漏检”。因此,最佳门限存在于区间[βmin,βmax]中。其次,门限值在这些等分值中依次从大到小搜索,直至某一值时,经霍夫变换能够检测到多层墙体直线,记下此时的门限值。该值即是理论上的最佳固定门限值。在用BP成像和改进的PCA分析方法预处理得到图像F后,检测算法的具体流程如下(这里以两层墙体成像为例说明):
1)确定最佳门限值的搜索范围[βmin,βmax]。
2)每搜索一个值βn,便以该值为门限对图像{F(x,y)}作二值化处理,1为目标区域,0为非目标区域,得到图像{B(x,y)};
3)初始化一块缓冲区,对应于极坐标参数平面,将其所有数据置为0;
4)对于二值化图像{B(x,y)}每一个值为1的像素点,求出极坐标参数平面对应的曲线,把这些曲线上的所有点的值都加1;
5)对在极坐标参数平面的倾斜角θ轴上[88°,92°]内的所有点作霍夫反变换,得到直角坐标系下的图像{FH(x,y)};
6)若{FH(x,y)}存在多于一个平行于坐标轴的像素为1的矩形区域,那么此时的βn即是最佳门限值,此时跳出循环,停止搜索,并记下矩形区域的位置坐标;否则,令n=n-1,重复步骤2~6;
7)记下β=βn,β即为最佳门限值。
得到最佳固定门限值β后,便可依此大致划分目标墙体区域和非目标杂波区域,以便后续强度补偿阶段的处理。步骤1~7的流程图如图3所示。
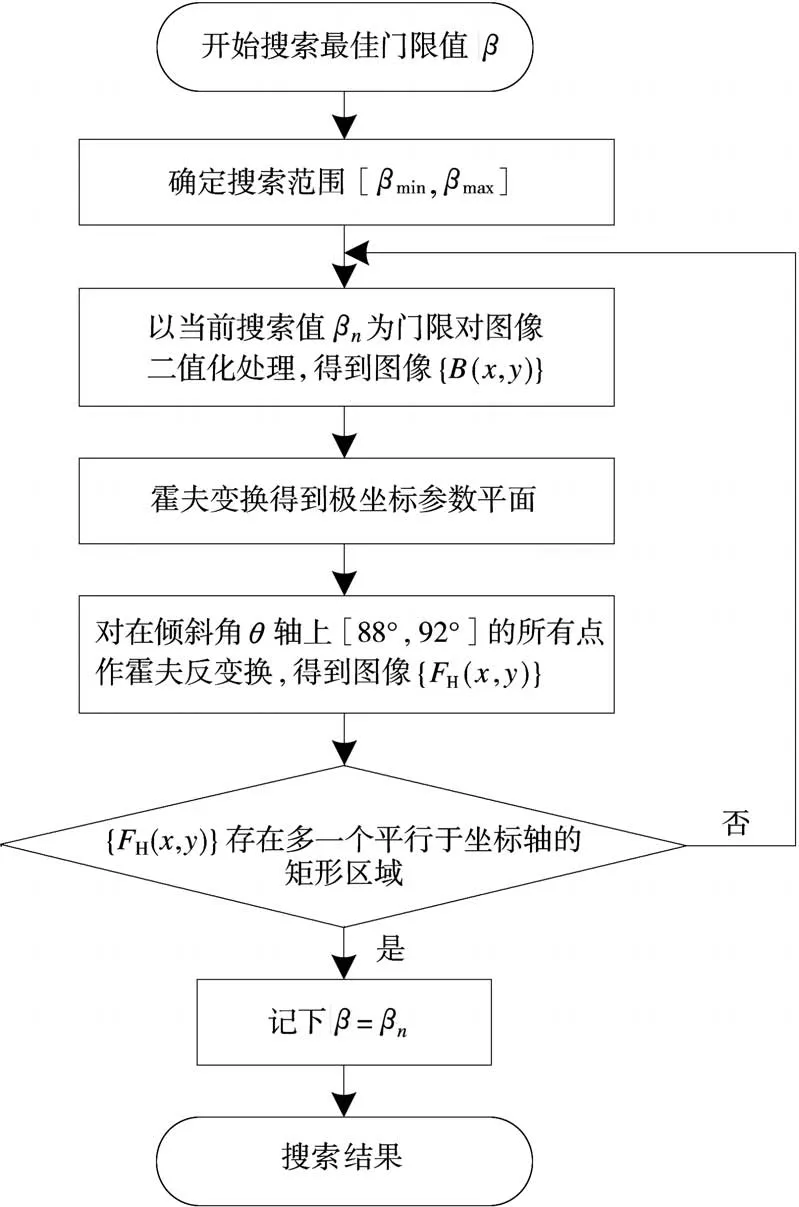
图3 固定门限β搜索流程图
2.2 墙体强度补偿阶段
本节介绍的算法是在固定门限β检测后所进行的墙体强度补偿算法。在为原始图像β给定归一化判决门限β后,可以得到二值化图像{B(x,y)}。可以说,根据二值化图像{B(x,y)}可以返回到对应的原始图像{F(x,y)},获得{F(x,y)}上墙体目标像素的位置信息和幅度信息,根据这些信息进行强度补偿。而获取这些信息,需要引入“数据连通域”和“深度优先搜索”这两个概念。
在一个数据矩阵里,对于某一个关注的数据a,它的周围存在8个数据a0~7(矩阵边界数据除外),如果这八个数据中的某一个a i(i∈0~7)与a的属性相同,则认为a和a i是连通的。如此类推,这样的一个以连通的数据构成的集合,称为数据连通域。在门限检测后的二值图像上,通常存在多个这样的数据连通域,这些数据连通域记载着目标像素的位置信息,而此时的数据连通域包含了全部的墙体目标的位置信息,回溯到原始图像{F(x,y)}上时,便可只针对数据连通域在{F(x,y)}上进行处理。
深度优先搜索(DFS)类似于树的前序遍历,优先往树状结构的深度方向搜索这一特性非常适用于图像数据连通域查找这一领域,并且具有边搜索边记录的特点,保证了在搜索的同时,获得每块数据连通域上对应目标的信息。
假设在对需要处理的单视角图像上使用DFS得到T块数据连通域,每块数据其幅度最大值为m i,所有数据连通域的最大值构成最大值集合{m1,m2,m3,…,m T},该集合中最大的元素为M,即,则补偿率为
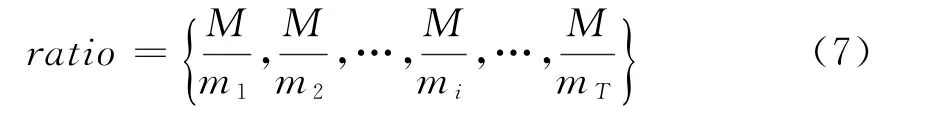
若ratio(i)代表第i个连通域的补偿率,那么第i个连通域相应原始图像{F(x,y)}位置坐标为(x,y)的像素点的值在补偿后为
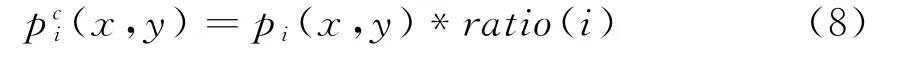
该阶段的算法步骤如下:
1)对原始图像{F(x,y)}使用固定门限β,将目标墙体区域和非目标杂波区域大致分离,得到二值化图像{B(x,y)};
2)对{B(x,y)}使用深度优先搜索,遍历整幅图像后只保留与检测阶段步骤6中得到的矩形区域位置坐标相同的数据连通域,即目标数据连通域,并记录下每块数据连通域的重要参数,如坐标和最大值;
3)利用式(8)对目标数据连通域上需要进行幅度补偿的像素进行处理。
其中步骤2中深度优先搜索的处理流程如图4所示。
整个流程可以由图5的框图表示。
3 实测数据结果验证
雷达系统发射信号类型为步进频,实验采用“走-停-走”的合成孔径方式进行场景成像,孔径合成路径平行于墙体,实验场景设置如图6所示,这里采用两层墙体成像为例。
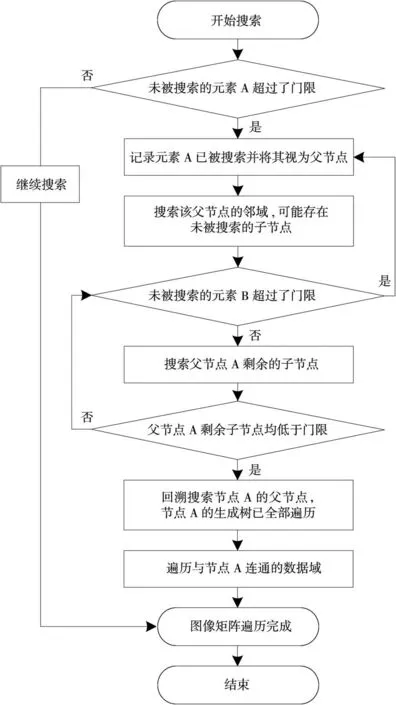
图4 深度优先搜索处理流程
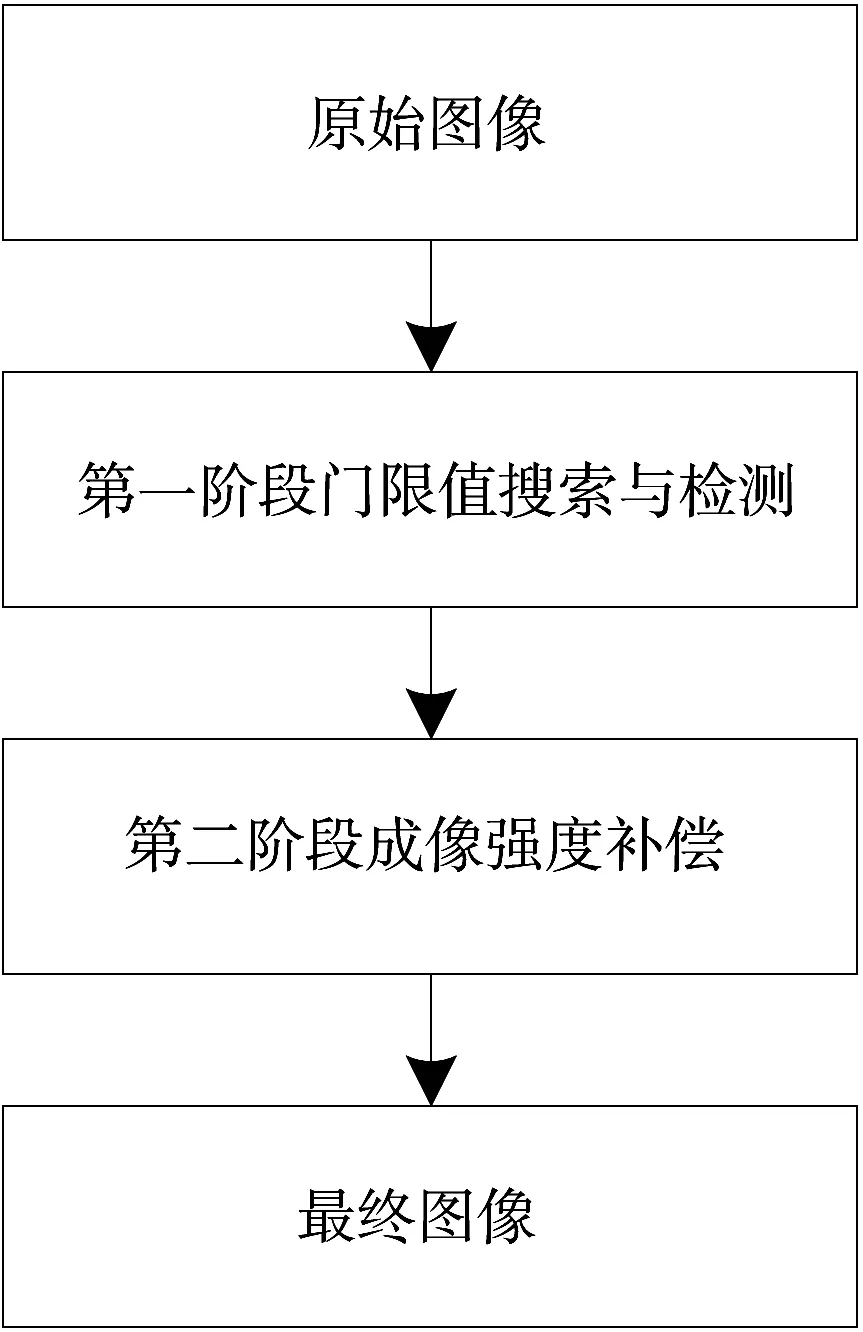
图5 本文提出的算法流程图
图6中黑点表示合成孔径路线天线的不同位置方位,发射信号步进频起始频点fstart=1 GHz,终止频点fstop=2 GHz,频阶Δf=2 M Hz,中心频率fc=1 GHz,单频持续时间T0=0.5μs,采用BP成像算法,并对成像结果采用基于PCA和模糊逻辑图像增强方法[1]处理图像,得到原始图像{F(x,y)},如图7(a)所示。
由图7(a)可以看出,由于第一层墙体wall1对信号的衰减,造成第二层墙体wall2的成像强度远低于第一层墙体,对后续的建筑布局重构带来困难。图7(b)是采用本文提出的基于霍夫变换门限检测的多层墙体成像强度衰减补偿方法的处理结果。可以看出,采用本文提出的算法,不仅完成了对第二层墙体wall2的检测,也较好地完成了对其的强度补偿。
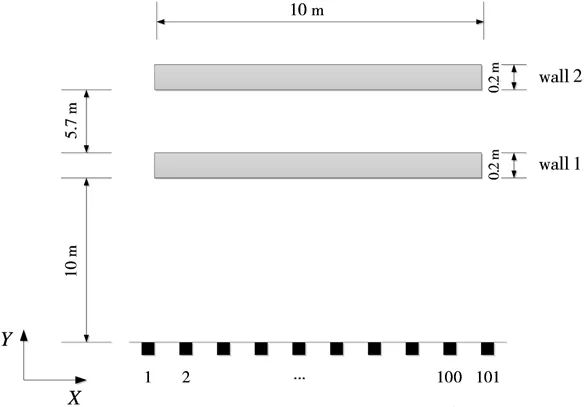
图6 实验场景设置
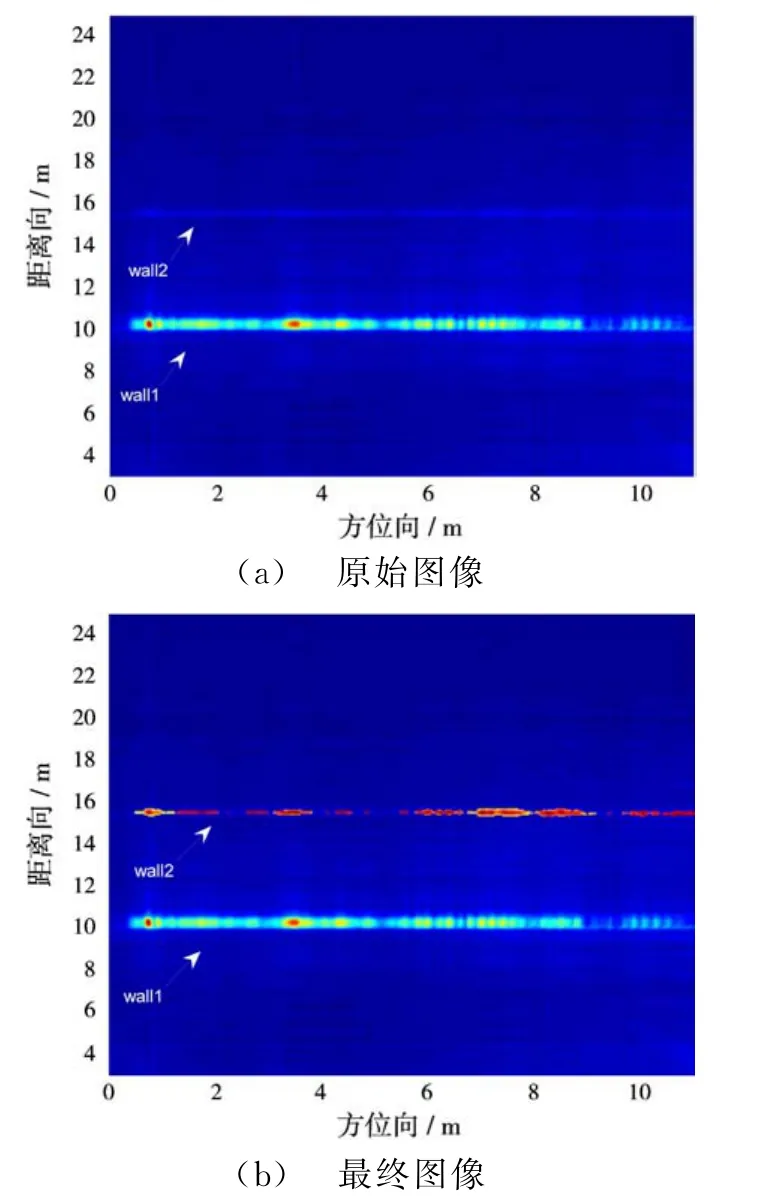
图7 处理前后对比图像
为量化体现本文算法的优越性,这里以均方误差MSE和峰值信噪比PSNR为例说明。均方误差越小,峰值信噪比越高说明图像与参考图像的差异越小,处理效果越好。首先给出背景抽取图像以作标准参考图像,如图8所示。
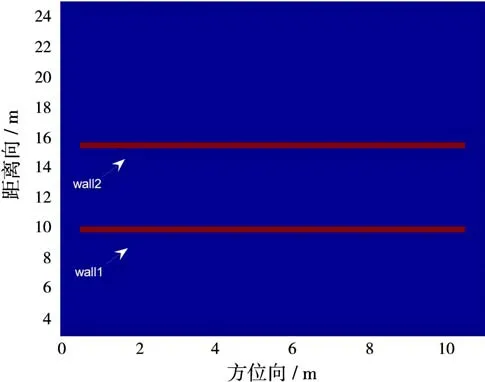
图8 背景抽取图像
记背景抽取图像矩阵为F bs,则均方误差MSE和峰值信噪比PSNR可以表示为
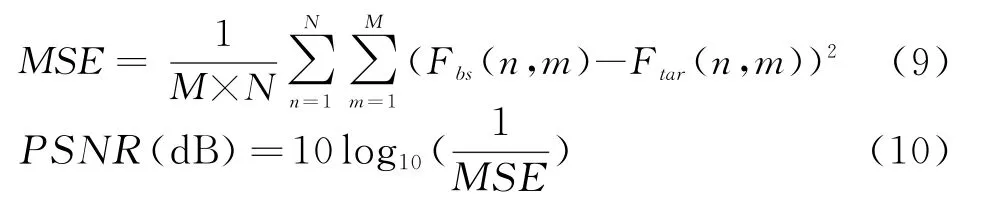
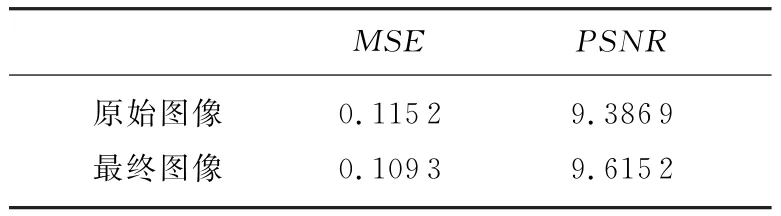
表1 图像处理前后的均方误差和峰值信噪比
由表1可以看出,运用本算法后图像的均方误差降低、峰值信噪比提高,说明图像运用本算法后更接近真实场景图像,定量上体现了该算法的优越性。
4 结束语
本文提出一种基于霍夫变换门限检测的多层墙体成像强度补偿算法,用于穿墙建筑布局成像中,该算法在杂波抑制、墙体补偿、提高信噪比等方面有很大优势,对改善图像质量方面有显著效果。该算法分为两个阶段,分别是墙体目标检测和墙体强度补偿。在墙体目标检测阶段,关键是确定合适的固定门限值,以区分目标墙体和非目标杂波。对此本文采用基于霍夫变换直线检测的算法搜索最佳门限值。在墙体强度补偿阶段,根据目标连通域的参数特性,获得相应连通域的补偿率,并对墙体强度进行补偿。实测数据处理结果验证了本文提出的算法的有效性和可行性。
[1]Yoon Y S,Amin M G.Through-the-Wall Radar Imaging Using Compressive Sensing Along Temporal Frequency Domain[C]∥2010 IEEE International Conference on Acoustics Speech and Signal Processing(ICASSP),Dallas,TX:[s.n.],2010:2806-2809.
[2]Smith G E,Mobasseri B G.Robust Through-the-Wall Radar Image Classification Using a Target-Model Alignment Procedure[J].IEEE Trans on Image Processing,2012,21(2):754-767.
[3]Debes C,Zoubir A M,Amin M G.Enhanced Detection Using Target Polarization Signatures in Throughthe-Wall Radar Imaging[J].IEEE Trans on Geoscience and Remote Sensing,2012,50(5):1968-1979.
[4]Lagunas E,Amin M G,Ahmad F,et al.Sparsity-Based Radar Imaging of Building Structures[C]∥2012 Proceedings of the 20th European Signal Processing Conference(EUSIPCO),Bucharest:[s.n.],2012:864-868.
[5]Lagunas E,Amin M G,Ahmad F,et al.Determining Building Interior Structures Using Compressive Sensing[J].Journal of Electronic Imaging,2013,22(2):021003.[6]Aftanas M,Drutarovsky M.Imaging of the Building Contours with Through the Wall UWB Radar System[J].Radio Engineering,2009,18(3):258-264.
[7]Nguyen L,Ressler M,Sichina J.Sensing Through the Wall Imaging Using the Army Research Lab Ultra-Wideband Synchronous Impulse Reconstruction(UWB SIRE)Radar[C]∥Proceedings of SPIE,Orlando,FL:[s.n.],2008:1-4.
[8]Ao Zhuojun,Kong Lingjiang,Jia Yong,et al.Multi-Channel Target Cooperative Detection in Through-the-Wall-Radar Imaging Based on Random Sparse Array[C]∥CIE International Conference on Radar,Chengdu,China:[s.n.],2011:176-178.
[9]Cui G,Kong L,Yang J.A Back-Projection Algorithm to Stepped-Frequency Synthetic Aperture Through-the-Wall Radar Imaging[C]∥1st Asian and Pacific Conference on Synthetic Aperture Radar,Huangshan:[s.n.],2007:123-126.
[10]赵彧,黄春琳,粟毅,等.超宽带穿墙探测雷达的反向投影成像算法[J].雷达科学与技术,2007,5(1):49-54.ZHAO Yu,HUANG Chun-lin,SU Yi,et al.BP Imaging Algorithm for UWB-TWDR[J].Radar Science and Technology,2007,5(1):49-54.(in Chinese)
[11]Riaz M M,Ghafoor A.Principle Component Analysis and Fuzzy Logic Based Through Wall Image Enhancement[C]∥Progress In Electromagnetics Research,[s.l.]:[s.n.],2012:461-478.

