基于Matlab Guide 的低通滤波器设计
常 巍,陈 玮
(1.中国电子科技集团公司第13 研究所市场营销部,河北石家庄 050051;2.中国电子科技集团公司第54 研究所,河北石家庄 050081)
模拟滤波器设计的关键是找到一个稳定易实现的逼近函数,且其幅频特性要满足所需滤波器的要求。常用的滤波器模型有巴特沃斯(Butterworth)滤波器、切比雪夫(Chebyscheff)滤波器、贝塞尔(Bessel)滤波器及椭圆函数(Elliptic)滤波器。虽这些滤波器设计过程均已较为成熟,但无论哪种设计过程却均需要繁琐复杂的计算,或使用大型设计软件,因此不便于使用。
Matlab[1]作为一种高性能数值计算和可视化的工程计算工具,其具有丰富的数学函数功能支持,并提供了丰富的用于模拟滤波器设计的函数,通过简单编程便可实现低通、高通、带通、带阻滤波器的设计,并能绘制出幅频和相频特性曲线[2]。因此,为简化滤波器设计,方便工程应用,本文提出了基于Matlab 的低通滤波器快速设计方法,利用Matlab 的图形用户界面工具Guide 实现了可视化。
1 低通滤波器设计
根据低通滤波器[1]所选逼近函数的不同,其也有不同的响应。图1(a)所示的响应通带顶部最平坦,故称为“最平坦响应”,也称作“Butterworth 响应”。图1(b)所示的响应通带衰减有规律性的起伏,且幅度相等,故称为“等波纹响应”,也被称作“Chebyscheff 响应”[3-4]。
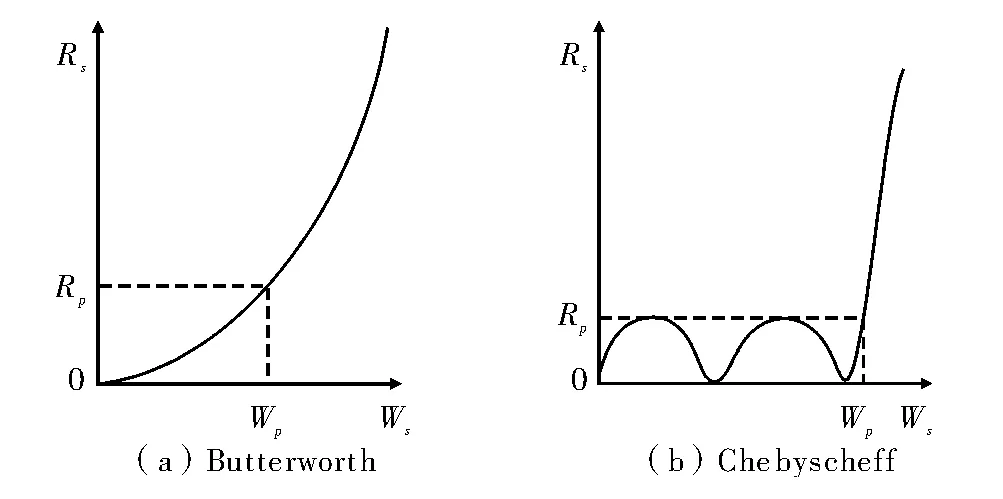
图1 低通滤波器的幅频特性曲线
图1 中Rs为阻带截止频率处的衰减,Ws为阻带截止频率,Rp为通带截止频率处的衰减,Wp是通带边缘上衰减为Rp时的频率,称为“带边频率”或“截止频率”,即可认为0 ~Wp为通带,Wp以上为阻带。
在设计好滤波器的逼近函数,确定滤波器阶数后,则要进行所需元件值的计算。下面以Butterworth 滤波器和Chebyscheff 滤波器为例,介绍这两种响应元件值的计算方法[5-6]。
1.1 Butterworth 滤波器元件值设计
图1(a)所示的Butterworth 滤波器数学表达式为
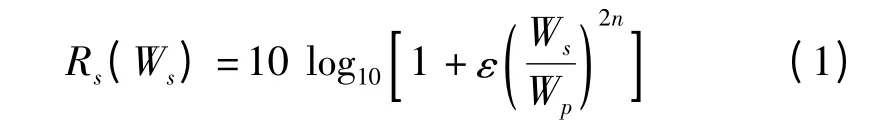
式中
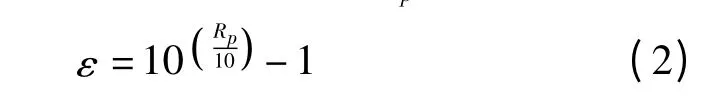
对于两端均接有电阻的Butterworth 低通滤波器,当Rp=3 dB 时,其归一化元件值可用下式得出
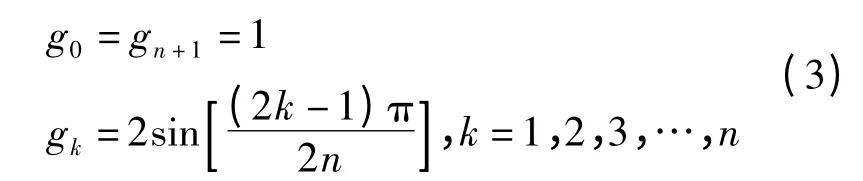
1.2 Chebyscheff 滤波器元件值设计
图1(b)所示的Chebyscheff 滤波器数学表达式为
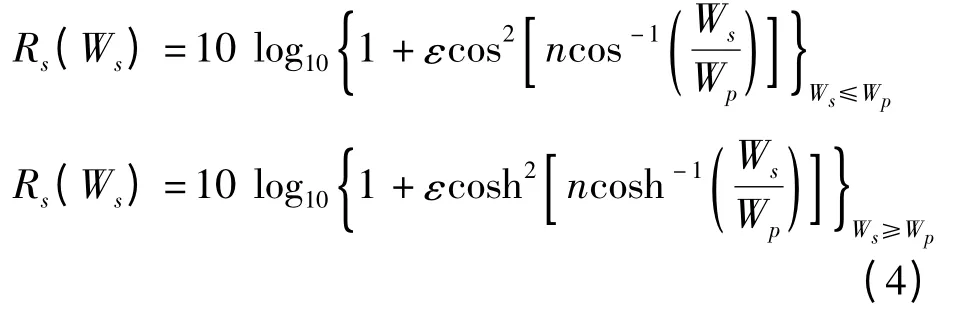
其中

式中,n 是该电路的电抗元件数目。若n 为偶数时,则Rs=0 dB 的频率有n/2 个;若n 为奇数,则Rs=0 dB的频率有(n+1)/2 个[8-10]。
对于两端均接有电阻的Chebyscheff 低通滤波器,设其通带波纹为Rp,g0=1,Wp=1,则其归一化元件值可用下式得出

式中
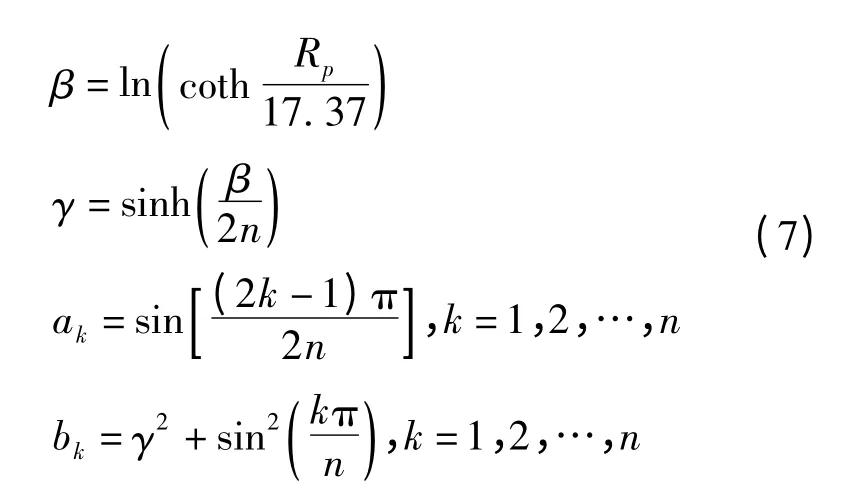
2 Matlab 图形用户界面
图形用户界面(Graphical User Interface,GUI)是目前计算机应用程序界面的主要形式。使用Matlab 的Guide 平台,用户可便捷地设计GUI 界面,并开发自己的应用程序。使用Guide 设计一个完整用户界面的基本过程如下[1]:
(1)设计功能。运用面向对象的方法,确定所需使用的对象,并添加到GUI 中。(2)完成布局。利用Guide 提供的布局工具,完成各对象的布局,力求界面友好、操作方便。(3)设置属性。打开各对象的属性查看器,设置相应属性。(4)编写回调函数。编写必要的回调函数(call-back),以保证所设计GUI 能正确响应用户操作。
3 界面设计
基于Matlab 的低通滤波器设计软件界面如图2 所示。其主要包括参数输入模块、类型选择模块、绘图模块、计算模块以及结果列表显示模块5 部分,可完成确定滤波器阶数、绘制幅频和相频特性曲线以及计算元件值功能。
滤波器类型可选择Butterworth 滤波器、Chebyscheff滤波器或Butterworth 滤波器及Chebyscheff 滤波器。通过输入通带截止频率Wp、阻带截止频率Ws、通带截止频率处的衰减Rp、阻带截止频率处的衰减Rs,可确定Butterworth 和Chebyscheff 滤波器的阶数、绘制幅频、相频特性曲线,并得出所需滤波器的元件值。

图2 界面设计
完成界面设计后,需编写相应GUI 对象的回调函数,以进行程序实现。
4 设计应用举例
4.1 参数输入
设计一个模拟信号输入低通滤波器,要求在40 Hz处的衰减为3 dB,在150 Hz 处的最小衰减为60 dB。
根据此设计要求,输入通带截止频率Wp=40 Hz、阻带截止频率Ws=150 Hz、通带截止频率处的衰减Rp=3 dB、阻带截止频率处的衰减Rs=60 dB。分别采用Butterworth 和Chebyscheff 滤波器进行计算。
4.2 确定滤波器阶数
使用Matlab 自带的滤波器计算函数,可较快得出滤波器的阶数。Butterworth 滤波器和Chebyscheff 滤波器计算函数分别如下

由此可得到,该低通滤波器按Butterworth 滤波器和Chebyscheff 滤波器设计得到的阶数分别为4 阶和5 阶。
4.3 绘制幅频、相频特性曲线
使用Matlab 还可绘制出滤波器的幅频和相频特性曲线。Butterworth 滤波器和Chebyscheff 滤波器所使用的函数分别如下

而绘制幅频、相频特性曲线的函数为
freqz(b,a,512,1 000);
最后得到按照Butterworth 滤波器和Chebyscheff滤波器设计的幅频和相频特性曲线分别如图3 所示,可根据所需低通滤波器的具体要求选择Butterworth 或Chebyscheff 加以实现。
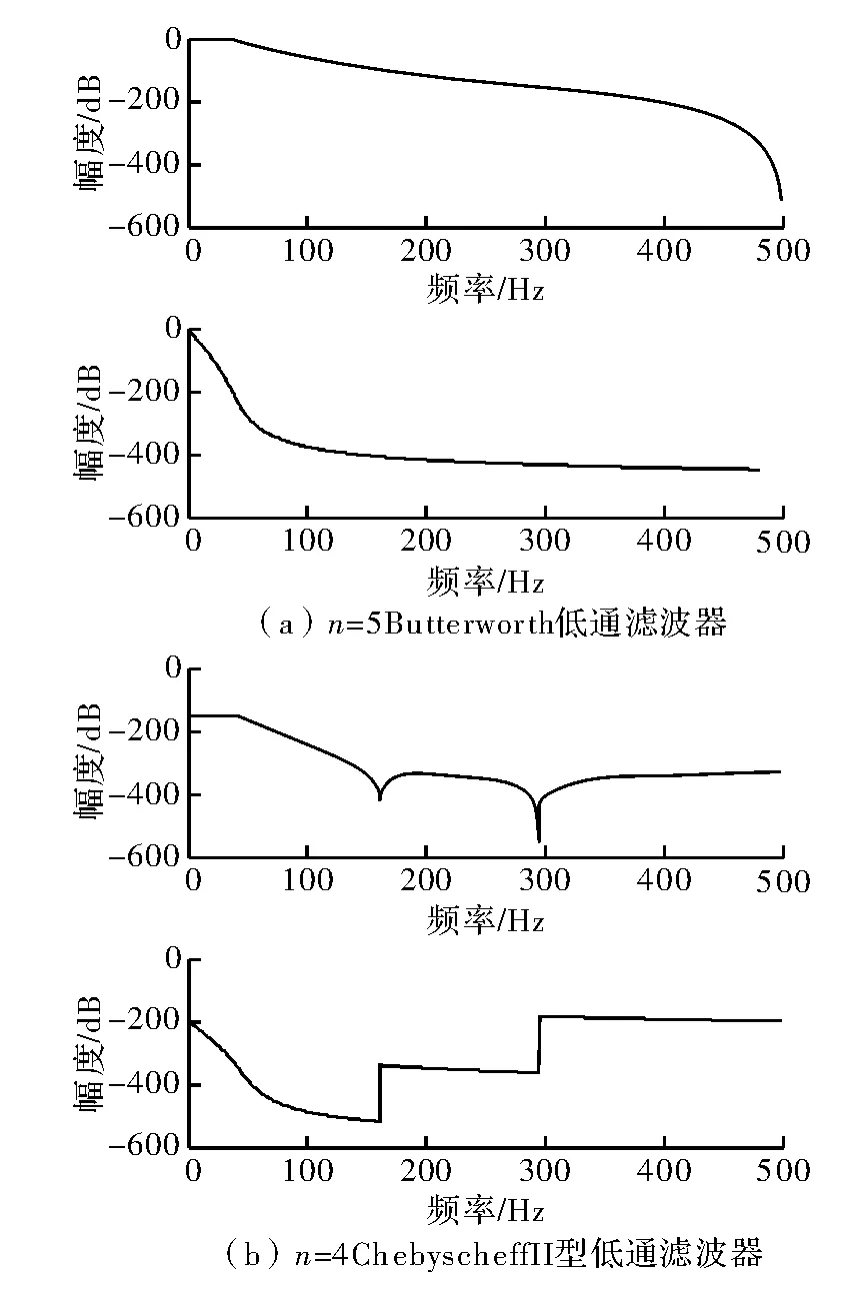
图3 滤波器幅频和相频特性曲线
4.4 计算元件值
Butterworth 滤波器和Chebyscheff 滤波器归一化元件值的计算如上所述,通过编程,可计算出所需滤波器的归一化元件值,如表1 所示。
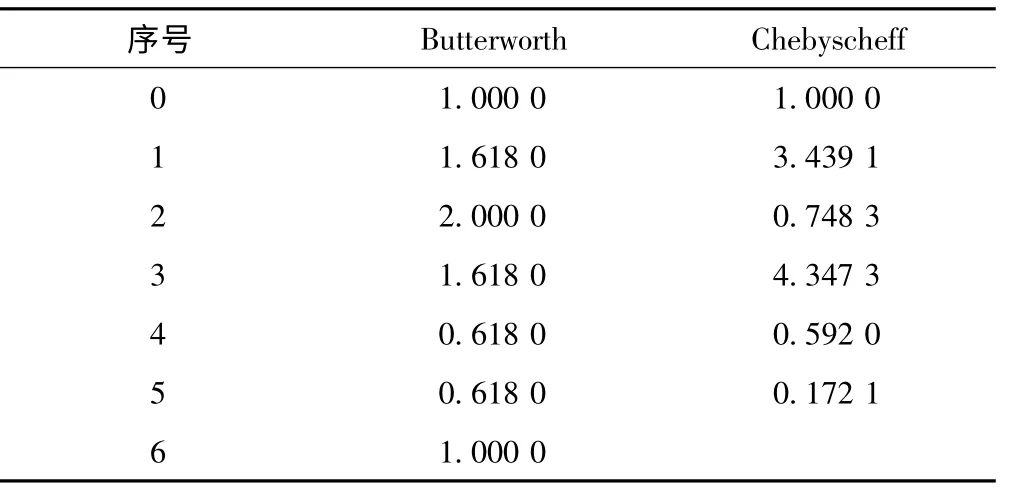
表1 所需滤波器的归一化元件值
使用低通滤波器设计软件,点击“计算”按钮,在界面右侧列表给出了所需滤波器的归一化元件值,如图4 所示。

图4 元件值计算结果列表输出
5 结束语
本文使用Matlab 的图形用户界面开发工具Guide,完成了模拟低通滤波器设计软件,其中包含参数输入、类型选择、绘图、计算以及结果列表显示5 大模块,并实现了确定滤波器阶数、绘制幅频和相频特性曲线以及计算元件值3 大功能。通过设计应用举例,按照Butterworth 和Chebyscheff 两种类型完成了所需的模拟低通滤波器的设计。
[1] 阮沈勇.MATLAB 程序设计[M].北京:电子工业出版社,2004.
[2] 高彩霞,高子余,艾永乐.基于MATLAB 的有源低通滤波器设计与实现[J].北京电子科技学院学报,2010(4):54-59.
[3] 王玉林,葛蕾,李艳斌.新型界面开发工具:MATLAB/GUI[J].无线电通信技术,2008,34(6):50-52.
[4] 雷前召.模拟低通滤波器的MATLAB 实现[J].湖南科技学院学报,2009(4):48-49.
[5] 李春红,王清芬.Ku 波段带通滤波器的设计与实现[J].无线电工程,2006(4):42-43.
[6] 甘本祓,吴万春.现代微波滤波器的结构与设计[M].北京:科学出版社,1973.
[7] 吴明英,毛秀华.微波技术[M].西安:西北电讯工程学院出版社,1987.
[8] 汤炜,朱信刚.微波超低相噪光电振荡器[J].半导体技术,2006(5):382-384.
[9] 李宏军,何艳丽.网络变换在滤波器设计中的应用[J].半导体技术,2002(5):15-17.
[10]RHEA R W.HF filter design and computer simulation[M].Sweden:Noble Publishing,1994.

