基于TDOA 无线定位的NLOS 误差抑制算法
王 正,陈 兵
(南京航空航天大学 计算机科学与技术学院,江苏 南京 210016)
随着网络通信技术的发展,无线定位被更多的学者所关注。在各种无线定位算法中,由非视距(Non Line of Sight,NLOS)传播造成的误差是主要来源[1]。因此,如何有效抑制NLOS 误差已成为无线定位研究中的关键问题。
目前对NLOS 误差抑制的主要方法有:采用LOS信号,LOS 重构[2-6]、加权算法[7-8]、带约束条件的最优化求解算法[9]等。本文研究了在NLOS 误差严重且误差模型不确定的场景下NLOS 误差抑制算法。基于卡尔曼滤波的NLOS 误差抑制算法主要思想是:通过上一时刻状态的估计值及当前状态的测量值来计算当前状态的估计值。卡尔曼滤波实时高效,在NLOS 误差严重的环境下无需过多先验信息就能保证一定精度,因此相比其他算法更适用于本文场景。但由于该算法只进行简单迭代,一次误差极大的测量值不仅会对当前定位产生影响,也将会对后续定位产生较大影响,因此传统卡尔曼滤波定位并不能保持较高的定位精度[10]。因此本文针对NLOS 基本误差特性对卡尔曼滤波的迭代过程进行了改进,获得了良好的性能。
1 相关工作
作为目前抑制NLOS 误差的热点,基于卡尔曼滤波的主流算法分为两类。一类是用传统偏差卡尔曼滤波进行NLOS 误差抑制,由于未考虑到NLOS 误差模型特性,因此在NLOS 误差较大的情况下此类算法定位精度较低。而另一类算法对卡尔曼滤波迭代过程做了改进,如文献[11]提出了一种将抗NLOS 加权重构引入到卡尔曼滤波中的定位算法,在一定程度上提高了定位精度及容错性,但由于卡尔曼滤波的误差累计特性,该算法的定位结果不能保持较高精度,特别是在NLOS 误差严重的环境中,该算法的精度提升并不明显。文献[10]提出了一种将无NLOS 误差的测量值与NLOS 误差作为系统的状态变量,利用卡尔曼滤波器对采样序列进行处理以抑制消除NLOS 误差的定位算法。该算法将测量值的特点和NLOS 误差特性运用到卡尔曼滤波器中效果较好,但该算法必须已知NLOS误差分布模型,这在实际场景中难以实现,特别是在NLOS 误差模型不确定的环境中,该算法效果较差。因此,在本文研究场景下,上述算法均不能保持较高的定位精度。
2 改进的卡尔曼滤波定位算法
2.1 TDOA 定位原理
在基于TODA(Time Difference of Arrival)的无线定位算法[12]中,首先需获得TODA 测量值。设参与定位的N 个锚节点坐标为(Xi,Yi),待定位节点坐标为(x,y),待定位节点到第i 个锚节点的距离为
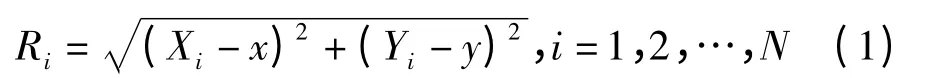
则第i 个锚节点到待定位节点的距离与主锚节点(X1,Y1)到待定位节点的距离差为
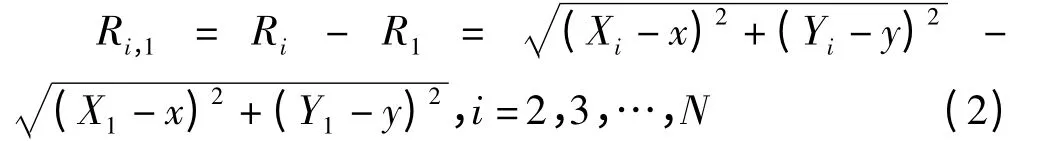
经等式变化可得

2.2 NLOS 误差模型
实际通信环境中,由于障碍物的遮挡,电波只能沿非直线路径传播,称为非视距传播,由此给带来的误差被称为非视距误差。因此,ti时刻待定位节点到第个锚节点之间的距离测量值Rm(ti)为
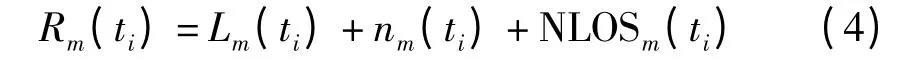
其中,Lm(ti)为真实距离;nm(ti)为服从N(μ,σ)分布的标准测量误差;NLOSm(ti)为正均值的随机NLOS 误差,在不同的信道环境中可能服从均匀分布、指数分布或Delta 分布[13]。
指数分布
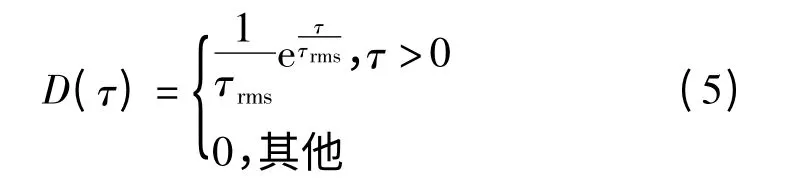
均匀分布

Delta 分布

2.3 改进的卡尔曼滤波
卡尔曼滤波主要由状态转移方程和测量方程组成

其中,s(k)为时刻状态向量;z(k)为时刻测量向量;A为采样间隔的状态转移矩阵;G(k)为测量矩阵;w(k)和v(k)为时刻噪声分量。式(9)和式(10)建立了k 时刻状态值、测量值与历史信息之间的关系,通过迭代即可根据测量值序列估计出相应时间点上的状态向量。迭代过程如下

其中,sk和s'k分别代表k 时刻状态向量的预测值和估计值;Pk和P'k分别代表时刻预测和估计误差的协方差矩阵;Q 和R 分别是w(k)和v(k)的协方差矩阵;αk是测量向量zk对应的信息过程;Kk是k 时刻卡尔曼增益。
由卡尔曼滤波的迭代过程可看出,状态的每一次更新均是由前一次的估计值和当前的测量值计算得到的,当某次测量值存在较大NLOS 误差时,后续的估计值也会受到较大影响,且卡尔曼滤波也将失去意义。因此,本文引入阈值T 用于判断当前测量值误差是否偏大。判断方法为:将计算所得信息与预设阈值T 进行比较,若信息较大,则说明当前测量值误差偏大,不应带入卡尔曼滤波进行迭代,故而舍去此次测量值,直接用预测值代替当前时刻估计值;若信息较小,这说明当前测量值误差在可接受范围内,可带入迭代过程计算当前估计值。另外,在本文研究的场景下,由于NLOS 为正向误差,所以计算得到的估计值相对于真实值存在一定的正向偏差。因此,本文引入修正系数θ 对测量值进行NLOS 正向误差修正,即将卡尔曼增益乘以修正系数θ 后再带入迭代过程。针对上述两点,本文改进了卡尔曼滤波算法,将原始算法迭代过程中式(14)修改为
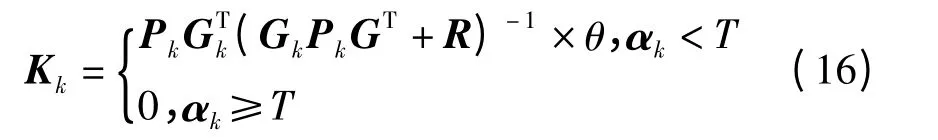
综上所述,本文算法中每一步迭代过程可描述如下:
步骤1 根据式(10)~式(12)计算出时刻状态预测值sk、预测误差协方差Pk、信息αk。
步骤2 将步骤1 中计算所得信息αk与预设阈值T进行比较,若αk<T,则根据式(16)计算卡尔曼增益值,并执行步骤3,否则直接将Kk值设为0,并执行步骤4。
步骤3 将2 中计算所得卡尔曼增益Kk值乘以修正系数θ。
步骤4 将卡尔曼增益值Kk带入式(14)~式(15)中计算,可得出k 时刻状态估计值s'k及估计误差协方差P'k,进而实现对目标节点的定位。
由于本文算法只在得到信息过程后根据信息对卡尔曼增益值进行修正,算法的时空复杂度相对于原卡尔曼算法并未有明显增加,从而保证了定位的时效性。
3 仿真结果及分析
在Matlab7.11 仿真平台上,对不同NLOS 误差模型进行定位仿真,并分别采用累计分布函数(Cumulate Distribution Function,CDF)及均方根误差(Root Mean Square Error,RMSE)作为评价算法定位性能的指标。其中,文献[10]算法中假定误差模型服从指数分布,即模型系数为1。由测量系统造成的误差服从均值为0 的高斯分布,每次仿真独立运行100 次。相邻时刻位置移动阈值取10 m,修正系数θ 取0.9。
3.1 指数分布NLOS 误差模型
图1 和图2 为NLOS 误差模型服从指数分布时,各算法性能比较。由图可知,此模型下文献[10]算法性能较好,这是因为该算法已假定NLOS 误差模型服从指数分布,并直接将该已知误差作为系统状态变量对误差进行消除。本文算法虽然相比文献[10]算法较差,但较原始卡尔曼算法及文献[11]算法更优,这是因为改进后算法对正向误差作出了修正,并通过阈值设定避免了较大误差测量值对定位结果的干扰。
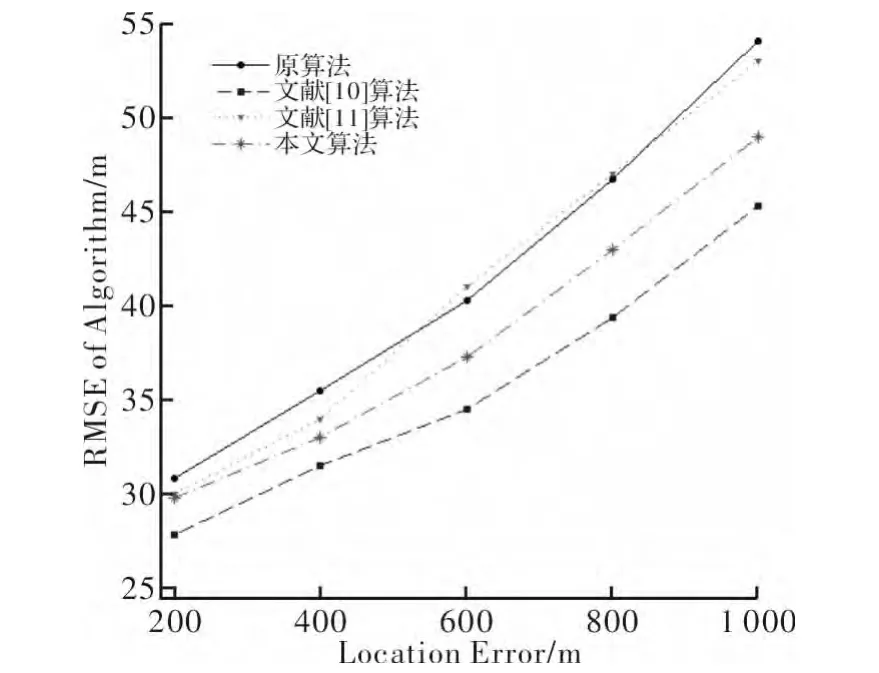
图1 NLOS 误差模型服从指数分布时不同小区半径下性能比较
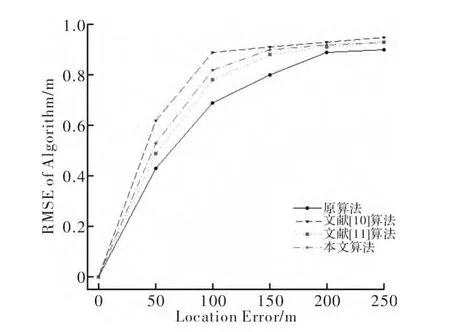
图2 NLOS 误差模型服从指数分布时CDF 性能比较
3.2 均匀分布NLOS 误差模型
图3 和图4 为NLOS 误差模型服从均匀分布时,各算法性能比较。由图可知,此模型下文献[10]算法性能较差,这是因为该算法已假定NLOS 误差模型服从指数分布,而事实上此时NLOS 误差模型服从均匀分布。本文算法通过修正系数减小NLOS 引起的正向测量误差,因此性能较原始卡尔曼算法及文献[11]算法更优。
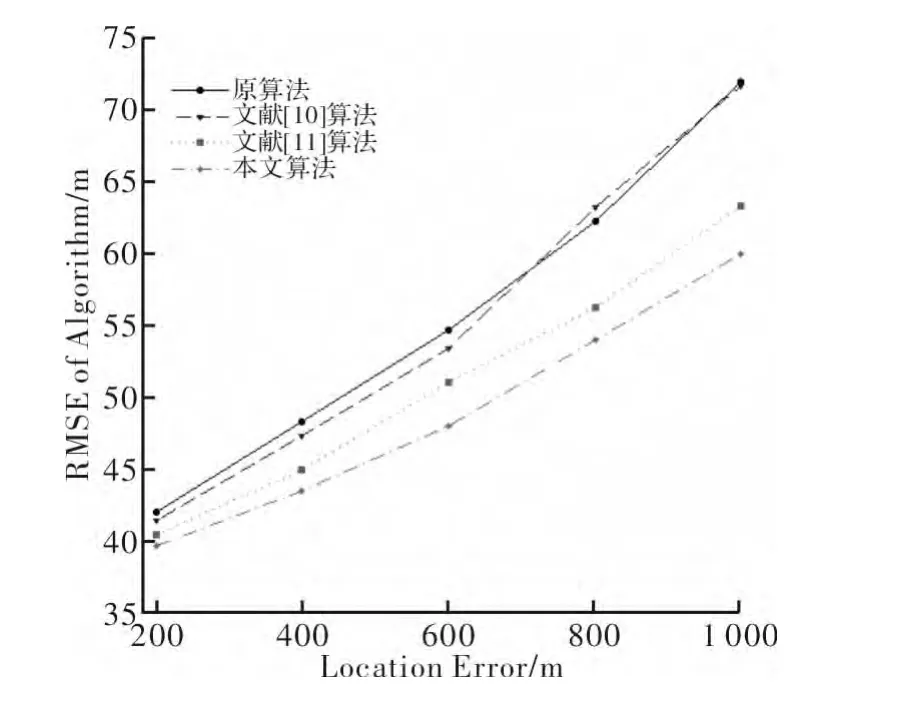
图3 NLOS 误差模型服从均匀分布时不同小区半径下性能比较

图4 NLOS 误差模型服从均匀分布时CDF 性能比较
3.3 Delta 分布NLOS 误差模型
图5 和图6 为NLOS 误差模型服从Delta 分布时,各算法性能比较。由图可知,此模型下文献[10]算法性能较差,原因与上节相同。本文算法通过修正系数减小NLOS 引起的正向测量误差,因此较原始卡尔曼算法及文献[11]算法更优。
由上述3 个不同误差模型下仿真结果比较可知,文献[10]算法在已知NLOS 误差模型的前提下能够极有效地抑制误差,并获得较高定位精度,但在误差模型未知的情况下,其性能不佳,因此不适用于NLOS 误差模型不确定的场景中。而文献[11]算法与原始卡尔曼滤波算法均未考虑迭代过程中误差的延续性,在NLOS 误差严重的场景下不能保持较高精度。综上所述,本文算法在NLOS 误差严重且误差模型不确定的场景下具有较好的综合性能。
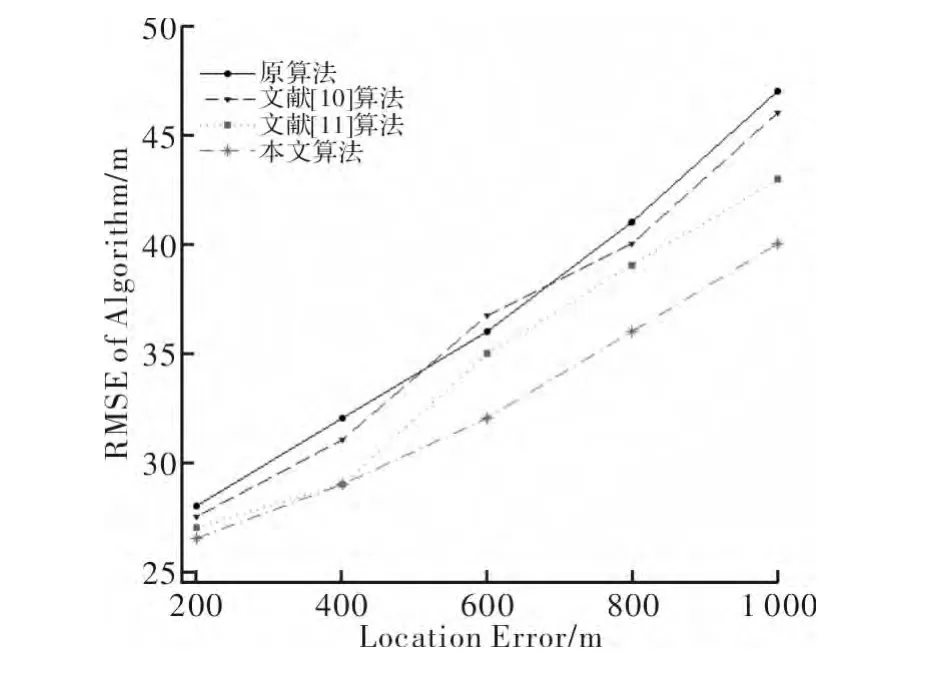
图5 NLOS 误差模型服从Delta 分布时不同小区半径下性能比较

图6 NLOS 误差模型服从Delta 分布时CDF 性能比较
4 结束语
本文在基于TDOA 的无线定位算法中,提出了一种能有效抑制NLOS 误差的卡尔曼滤波改进算法。通过研究误差特性,针对较大NLOS 误差会导致后续估计值均受严重影响引入信息阈值,而针对NLOS 误差必为正向偏差的特性引入修正系数,进而对卡尔曼滤波迭代过程进行改进,以获得更准确的估计值。仿真结果表明,在NLOS 误差严重且误差模型不确定的环境下,本算法性能较其他基于卡尔曼滤波的定位算法有所提升。
[1] CAFFERY JR J,STUBER G L.Subscriber location in CDMA cellularnetworks[J].IEEE Transactions on Vehicular Technology,1998,47(2):406-416.
[2] MARILYNN P,WYLIE J H.The non-line of sight problem in mobile location estimation[C].5th IEEE ICUPC,1996(2):827-831.
[3] YANGSEOK J.Calibration of NLOS Error for Positioning Systems[R].USA:IEEE Vts Vtc 2001.
[4] DENG Pin,LIU Lin,FAN Pingzhi.An NLOS error mitigation scheme based on TDOA reconstruction for cellular location service[J].电波科学学报,2003,3(18):311-316.
[5] URRUELA H.NLOS mitigation based on a trellis search for wireless location[C].Proc.of the 6th IEEE Workshop on Signal Processing Advances in Wireless Communications,2005.
[6] MA Changlin.Non-line-of-sight error mitigation method for TOA measurements[J].IEEE Transactions on Vehicular Technology,2007,56(2):641-645.
[7] LI Cong,WEI Huazhuang.Non-line-of-sight error mitigation in tdoa mobile location[C].San Antonio USA:Proc.IEEE Globecom,2001:680-684.
[8] CHEN P C.A non-line-of-sight error mitigation algorithm on location estimation[C].New Orleans,USA:WCNC'99,1999:316-320.
[9] VENKATRAMAN S,CAFFERY J,YOU H R.Locating using LOS Range Estimation in NLOS Environments[C].UK:IEEE VTC'2002,2002:856-860.
[10]张美杨,季仲梅,王建辉.基于Kalman 滤波器的非视距误差抑制算法[J].计算机工程,2010(11):291-292.
[11]孙克辉,蔡永棋.NLOS 环境下的卡夫曼滤波跟踪定位算法[J].微计算机信息,2009(21):163-165.
[12]谷静,李明远.蜂窝移动通信网络中的无线定位技术[J].现代电子技术,2004(1):68-70.
[13]HALL D L,LINAS J.An introduction to multi-sensor data fusion[J].Signal Proceding IEEE,1997,85(7):6-23.

