FGM相依结构下随机变量关于最值的次指数性

刘 庆 庆

(安徽大学 数学科学学院，安徽 合肥 230601)



FGM相依结构下随机变量关于最值的次指数性

刘 庆 庆

(安徽大学 数学科学学院，安徽 合肥 230601)

文章主要研究FGM(Farlie-Gumbel-Morgenstern)相依结构下两个次指数随机变量的最小值、最大值关于次指数族的封闭性。证明了FGM相依结构下两个次指数随机变量的最小值总是次指数的，得到了两个次指数随机变量的最大值也是次指数的充分必要条件，推广了文献[9]的结果。

FGM相依结构；次指数分布；最小值；最大值

近年来，有关重尾分布的性质及其在风险管理中的应用研究受到广泛的关注。统计学、排队论等诸多领域次指数分布[1]作为一类重要的重尾分布，不仅有非常重要的理论意义，还有迫切的实际应用价值。对于次指数分布来说，常见的有Weibull分布以及Lognormal分布，其中Weibull分布是可靠性分析及寿命检验的理论基础，Lognormal分布常为股票投资者分析判断市场行情并做出预测提供重要依据。关于次指数分布在运算下关于次指数族的封闭性研究由来已久，Embrechts等[2]证明了两个独立的次指数分布的卷积封闭性；Cline等[3]给出了两个独立的次指数分布乘积关于次指数分布族的封闭性若干充分条件，此结论随后得到进一步推广[4-6]；Yakymiv利用次指数分布的若干理论结果[7-8]，证明了两个独立的次指数分布在最小值运算下仍然是次指数的，并给出了两个独立的次指数分布在最大值运算下关于次指数族封闭的充要条件。

然而，以上关于次指数分布的结论大都集中在独立性假设下，虽然这一假设在数学处理上会带来极大的方便，但它却与客观实际严重不符，同时也会影响到结果的适用性。因此， 近年来在各类相依结构下研究次指数分布的性质成为热点。本文在前人工作的基础上，假定两个次指数分布服从FGM(Farlie-Gumbel-Morgenstern)相依结构[9]，分别研究这两个次指数分布在最小值、最大值运算下关于次指数族的封闭性，所得结果推广了文献[9]的结论。

下面先介绍一些相关定义、引理等知识。

定义1[1]称非负随机变量X(或其分布函数F)为次指数分布，记作X∈S(或F∈S)，如果

(1)

其中，F2*表示分布函数F的二重卷积。

注1如果设X1,X2为两个独立同分布的非负随机变量服从共同的分布F，则(1)式等价于P(X1+X2>x)～P(max{X1,X2}>x)，此即X1与X2最大和等价。

定义3[9]如果(X,Y)的联合分布为P(X≤x,Y≤y)=C[F(x),G(y)]，其中

C(u,v)=uv+ruv(1-u)(1-v),r∈(-1,1),

其中F(x),G(y)分别为X与Y的边际分布，那么称(X,Y)服从FGM相依结构。

注2在定义3中若取r=0，则FGM相依结构退化为X与Y相互独立情形。

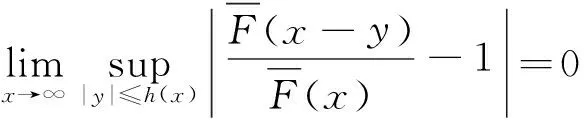
引理2[8]若X和Y相互独立，X,Y∈S，h(x)是满足引理1的任意函数，那么X+Y∈S，当且仅当

下面是本文的主要结论及证明。

定理1设X，Y为两个满足FGM相依结构的非负随机变量， 如果X,Y∈S，则X∧Y∈S。

证明因为H1为X∧Y的分布，由文献[6]可知H1的尾概率可以表示为

(1+θ)P(X*∧Y*>x)-

此外，

[2+o(1)]P(X*∧Y*>x)

类似地，有

[2+o(1)]P(X*∧Y*>x)

(3)

[4+o(1)]P(X*∧Y*>x)

(4)

综合(2)-(4)式可得，

由文献[9]可知X*∧Y*∈S，根据次指数分布族在尾等价下的封闭性，可得X∧Y∈S。

定理2设X，Y为满足FGM相依结构的非负随机变量，如果X，Y∈S，则X∨Y∈S当且仅当

证明因为H2为X∨Y的分布，由文献[6]可知H2的尾分布可以表示为

(1+θ)P(X*∨Y*>x)-

(1+θ)I1-θI2-θI3+θI4。

(5)

其中，对于I2有

[2+o(1)]P(X*>x)+P(Y*>x)-

[2+o(1)]P(X*>x)P(Y*>x)=2P(X*>x)+2P(Y*>x)-2P(X*>x,Y*>x)-P(Y*>x)+o(1)P(X*>x)=2P(X*∨Y*>x)-P(Y*>x)+o(1)P(X*>x)

(6)相应地，

I3=2P(X*∨Y*>x)-P(X*>x)+

o(1)P(Y*>x)

(7)

对于I4，相应地有I4=[2+o(1)]P(X*>x)+

[2+o(1)]P(Y*>x)-

[2+o(1)][2+o(1)]P(X*>x)P(Y*>x)=

4P(X*>x)+4P(Y*>x)-4P(X*>x,Y*>x)-2[P(X*>x)+P(Y*>x)]+o[P(X*>x),Y*>x]=

4P(X*∨Y*>x)-2[P(X*>x)+P(Y*>x)]+

o[P(X*>x)+P(Y*>x)]

(8)

将(6)-(8)式代入(5)式可得

P(X∨Y>x)=(1+θ)P(X*∨Y*>x)-

θ[P(X*>x)+(Y*>x)]+

o(1)[P(X*>x)+(Y*>x)]～

P(X*∨Y*>x)+o(1)P(X*∨Y*>x)。

要证明X∨Y∈S等价于证明X*∨Y*∈S，由于X*,Y*相互独立且分别同分布于X,Y，根据文献[8]知X*∨Y*∈S⟺X*+Y*∈S，再由引理2可知

[1] Emberchts P, Klüppelberg C, Mikosch T. Modelling Extremal Events for Insurance and Finance [M]. Berlin Heidelberg: Springer-Verlag, 1997.

[2] Embrechts P, Goldie C M. On closure and factorization properties of subexponential distributions[J]. Journal of the Australian Mathematical Society, 1980, 29: 243-256.

[3] Cline D B H, Samorodnitsky G. Subexponentiality of the product of independent random variables[J]. Stochastic Processes & Their Applications, 1994, 49(1): 75-98.

[4] Chen Y, Su C. On the behavior of the product of independent random variables[J]. Science in China Series A, 2006, 49(3): 342-359.

[5] Tang Q. The subexponentiality of products revisited[J]. Extremes, 2006, 9(3-4): 231-241.

[6] Chen Y. The finite-time ruin probability with dependent insurance and financial risks[J]. Journal of Applied Probability, 2011, 48(4): 1035-1048.

[7] Yakymiv A L. Sufficient conditions for the subexponential property of the convolution of two distributions[J]. Mathematical Notes, 1995, 58(5): 1227-1230.

[8] Yakymiv A L. Some properties of subexponential distributions[J]. Mathematical Notes, 1997, 62(1):116-121.

[9] Geluk J. Some closure properties for subexponential distributions[J]. Statistics Probability Letters, 2009, 79(8): 1108-1111.

[10] Foss S, Korshunov D, Zachary S. An Introduction to Heavy-Tailed and Subexponential Distributions[M]. New York: Springer, 2011, 38.

Subexponentiality under the Operation of the Minimum and Maximum for FGM Dependent Random Variables

LIU Qing-qing

(School of Mathematical Sciences, Anhui University, Hefei, Anhui 230601, China)

This paper mainly studies the closure properties about the subexponential class for the minimum and maximum of two subexponential random variables according to FGM dependence structure. It is proven that, under FGM dependence structure, the minimum of two subexponential random variables is still subexponential. Furthermore, in the same case, the sufficient and necessary condition of the maximum of two subexponential random variables is subexponential.The obtained results generalize the case of reference[9].

FGM dependence structure; subexponential distribution; minimum; maximum

2015-10-29

安徽省高等学校自然科学研究基金(KJ2014A020)。

刘庆庆，男，安徽阜阳人，安徽大学数学科学学院硕士研究生，研究方向为金融数学。Email:1187761765@qq.com

时间：2016-8-17 11:31

http://www.cnki.net/kcms/detail/34.1150.N.20160817.1131.009.html

O211.4

A

1007-4260(2016)03-0028-03

10.13757/j.cnki.cn34-1150/n.2016.03.009