多涡卷Jerk 混沌吸引子的EWB 仿真

徐礼国，徐小云

(广州大学 华软软件学院，广东 广州 510990)

混沌信号因其对初始条件的高度敏感、非周期等复杂动力学特性，被应用于保密通信、数字加密等领域［1］。多涡卷混沌吸引子与超混沌吸引子具备更为复杂的动力学特性，目前已成为非线性电路与系统领域的研究热点，并被认为具有更高的研究价值和应用前景。如何产生出多涡卷混沌吸引子及能否用物理器件实现是研究的首要问题。近年来，国内外学者在这一领域的研究取得了一些成果［2－11］。

本文在文献［3］理论成果的基础上，利用阶梯波函数从理论上产生出多涡卷Jerk 混沌吸引子，并利用EWB 电路仿真软件，设计出具体仿真电路对理论分析进行验证。仿真结果表明，用阶梯波函数产生多涡卷Jerk 混沌吸引子的方法是可行的，且该方法产生的多涡卷Jerk 混沌吸引子是可物理实现的。

1 双涡卷Jerk 混沌系统

1.1 双涡卷Jerk 混沌吸引子产生机理

Jerk 混沌系统的状态方程为

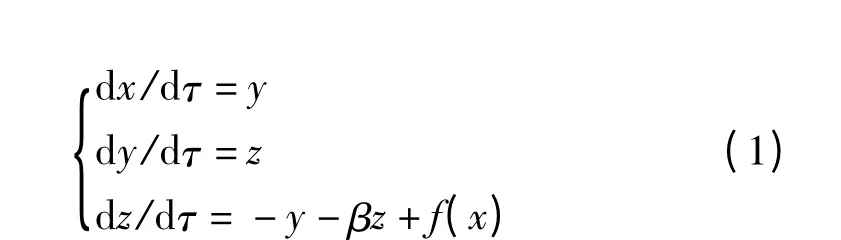
式中，参数β=0.45 ～0.7，x，y，z，τ 均为无量纲变量，故式(1)为无量纲状态方程。当时，可产生单涡卷混沌吸引子;当f(x)=sgn(x)－x 时，可产生双涡卷混沌吸引子。下面以f(x)=sgn(x)－x 为例，分析双涡卷混沌吸引子的产生机理。

首先，注意到式(1)中函数f(x)=sgn(x)－x 的波形为锯齿波，若令F(x)=sgn(x)，则F(x)是阶梯波，只需通过增加或减少一个线性函数后，其之间便可相互转换。

根据锯齿波与阶梯波之间的变换，进一步得式(1)变换后的形式为

此时式(2)中的F(x)=sgn(x)为符号函数。

根据混沌系统平衡点理论，令式(2)等号左边为0，得系统的平衡点方程为由式(3)可得两个指标2 的鞍焦平衡点，具体坐标不再解出，平衡点对应的Jacobi 矩阵为

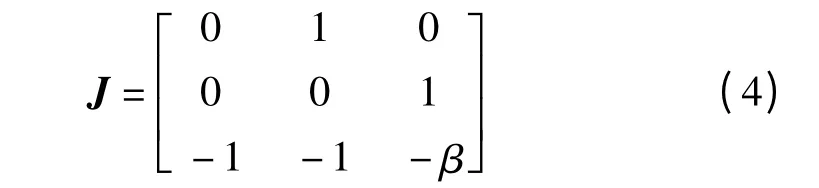
式中β=0.6。得对应的特征值为

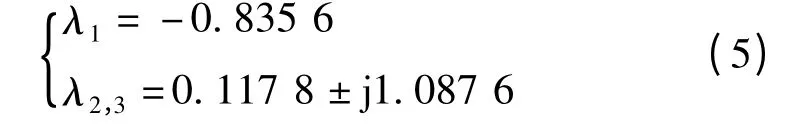
每个鞍焦平衡点能产生一个涡卷，故上述系统能产生双涡卷混沌吸引子。

1.2 双涡卷Jerk 混沌吸引子的电路仿真

为了能用EWB 仿真软件设计出式(2)所对应的仿真电路，在式(2)的基础上引入时间尺度变换因子1/R0C0，且令τ=t/R0C0，进行微分积分转换后的方程为

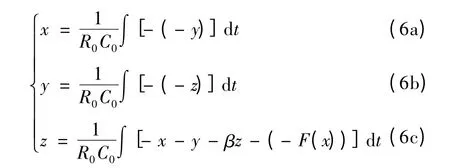
变换后的方程由集成运算放大器TL082 构成的反相积分电路、反相比例加法电路及比较器电路实现。

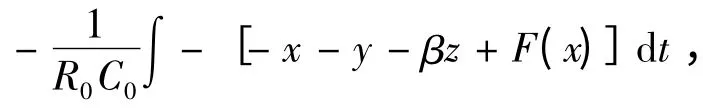
图1 式(6)中式(c)的仿真电路

非线性函数F(x)=sgn(x)的产生可由比较器和比例反相器实现，原理较简单，可参考式(6c)仿真电路的设计方法，其仿真电路如图2 所示。因为TL082 供电电源为±15 V 时，比较器的饱和输出电压为±13.5 V，所以比例反相器的比例系数为R21/R22=1/13.5 时，即可输出符号函数F(x)=sgn(x)。

图2 非线性函数的产生电路

用仿真软件EWB 中的相图分析工具，可得到如图3所示双涡卷混沌吸引。

图3 双涡卷吸引子相图

2 多涡卷Jerk 混沌系统

文献［3］中提出对于某些混沌系统通过扩展某一方向上指标2 鞍焦平衡点，可使混沌系统产生多涡卷混沌吸引子。本文在双涡卷Jerk 系统的基础上，利用阶梯波函数来扩展x 方向上的指标2 的鞍焦平衡点，将双涡卷系统变成多涡卷系统，这是在多涡卷混沌系统产生方式上的一种不同方法。其主要特点是，鞍焦平衡点的个数与涡卷的个数相等，且根据非线性函数的对称性，即非线性函数F(x)具有奇对称的特点，在原点的两边扩展出相同的指标2 的鞍焦平衡点。

2.1 偶数个多涡卷Jerk 混沌吸引子的产生

非线性函数F(x)的不同形式，决定了式(2)中指标2 的鞍焦平衡点个数，若要产生偶数个涡卷，非线性函数F(x)的具体表达式为

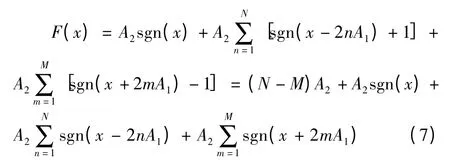
式中，N，M=1，2，3，…。若N=M，则

注意到在实际情况中，可考虑A2=A1=A，A 是＞0的可调参数，实际上A 就是变量比例压缩变换中的压缩系数。通过调节A 的大小，可改变涡卷本身的大小，即A 越小时，涡卷的大小则越小，从而在±13.5 V 的范围内，能产生的涡卷数量更多，反之亦然。根据上述分析，可将式(8)进一步简化为

结合式(2)和式(9)，得产生(2N+2)个涡卷的Jerk 系统状态方程为

式(10)中参数β=0.45 ～0.7，可根据实际需要确定其大小。

注意到式(10)中的非线性函数F(x)可产生(2N+2)个阶梯，为进一步理解，不妨假设式(9)中的A=0.5，N=2，则阶梯的数量为2N+2=2×2+2=6。

同前面双涡卷系统平衡点的分析过程相同，令式(10)中等式的左边为0，令A=0.5，N=2，可得系统有6 个指标2 的鞍焦平衡点，每个鞍焦平衡点能产生一个涡卷，故系统能产生6－涡卷。平衡点的具体坐标不再解出，对应的Jacobi 矩阵和特征值也不再求解。

图4 所示是A=0.5，N=2 时，式(10)中非线性函数F(x)的仿真电路，式(10)中其他3 个等式的仿真电路与双涡卷Jerk 系统，即式(6)的仿真电路相同，故不再重复给出。6－涡卷混沌吸引子相图如图5 所示。

图4 6－阶梯波非线性函数产生电路

图5 6－涡卷混沌吸引子相图

2.2 奇数个多涡卷Jerk 混沌吸引子的产生

若在式(2)对应的混沌系统中产生奇数个涡卷，非线性函数F(x)的具体表达式为

式(11)中N，M=1，2，3，…。尤其是当N=M，A2=A1=A 时，则

与偶数个涡卷的产生相似，式(12)中的非线性函数F(x)产生(2N+1)个阶梯，假设式(12)中A=0.5，N=3，则阶梯的数量为2N+1=2×3+1=7，可使式(6)对应的混沌系统产生7－涡卷。7－阶梯波非线性函数F(x)的仿真电路如图6 所示，7－涡卷混沌吸引子相图如图7 所示。

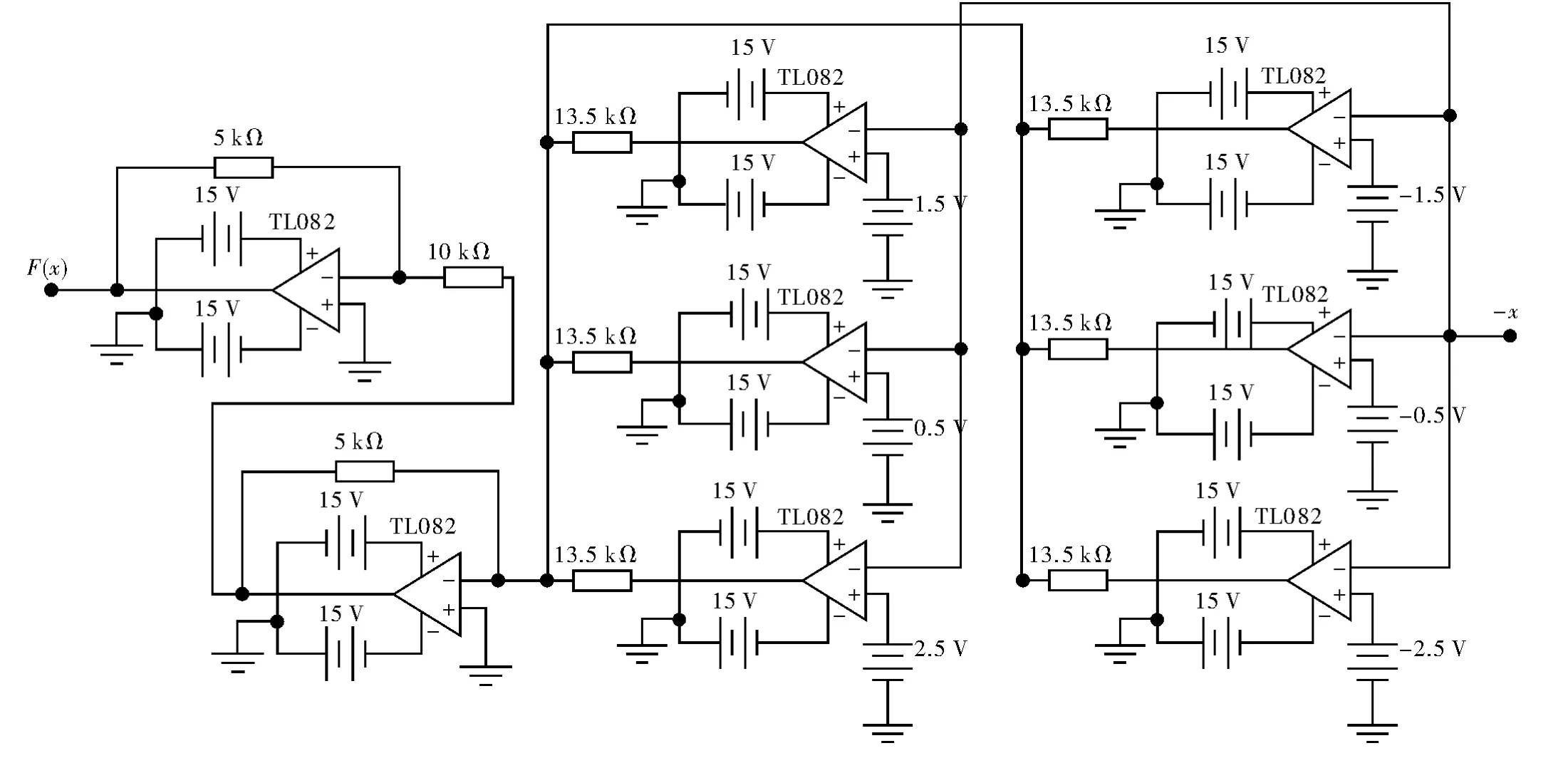
图6 7－阶梯波非线性函数产生电路

图7 7－涡卷混沌吸引子相图

3 结束语

本文在双涡卷Jerk 混沌吸引子的基础上，利用阶梯波函数构造产生出多涡卷Jerk 混沌吸引子，分析了多涡卷Jerk 混沌吸引子产生的机理，并根据无量纲状态方程，分别设计了6－涡卷和7－涡卷混沌吸引子仿真电路。同时利用EWB 进行了仿真验证，仿真结果与数学分析结果一致，进一步证实了多涡卷Jerk 系统的存在。因仿真电路中所用器件与实际硬件电路器件几乎相同，仿真结果即表明了多涡卷Jerk 混沌吸引子是可物理实现的，为多涡卷Jerk 混沌系统下一步的研究及实际应用打下了基础。

［1］ CHEN G R，YU X H.Chaos control theory and applications［M］.Berlin:Germany Spring－Verlag，2003.

［2］ 禹思敏，丘水生，林清华.多涡卷混沌吸引子研究的新结果［J］.中国科学:E 辑，2003(4):365－374.

［3］ YU S M，LÜ J H，LEUNG H，et al.Design and Implementation of n－scroll chaotic attractors from a general jerk circuit［J］.IEEE Transactions on Circuits and Systems I，2005，52(7):1459－1476.

［4］ LÜ J，CHEN G.Multi－scroll chaos generation:theories，methods and applications［J］.International Journal of Bifurcation and Chaos，2006，16(7):775－858.

［5］ LÜ J H，YU S M，LEUNG H，et al.Experimental verification of multi－directional multi－scroll chaotic attractors［J］.IEEE Transactions on Circuits and Systems I，2006，53(1):149－165.

［6］ 禹思敏.用三角波序列产生三维多涡卷混沌吸引子的电路实验［J］.物理学报，2005(4):1500－1509.

［7］ ZHENG B D，ZHENG H F.Bifurcation analysis in delayed feedback Jerk systems and application of chaotic control［J］.Chaos Solitons Fractals，2009，40(3):1190－1206.

［8］ 李清都，杨晓松.三维混沌信号产生器的设计［J］.电子学报，2007，35(3):497－500.

［9］ 李亚，禹思敏，戴青云，等.一种新的蔡氏电路设计方法与硬件实现［J］.物理学报，2006，55(8):3938－3943.

［10］王光义，丘水生，陈辉，等.一个新的混沌系统及其电路设计与实现［J］.电路与系统学报，2008，13(5):58－60，65.

［11］刘凌，苏燕辰，刘崇新.一个新混沌系统及其电路仿真实验［J］.物理学报，2006，55(8):3933－3936.