基于点电源的船舶静态电场深度换算方法研究

姜润翔 胡英娣 龚沈光

（1.海军工程大学兵器工程系，湖北 武汉430033；2.中国人民解放军91872部队，北京100071）

引 言

为了有效地解决船舶静电场的深度换算问题，前提是建立正确的正演模型，在此基础上，通过实测数据建立关于场源信息的超定方程组，而后利用最优求解算法求解场源，最后利用反演后的场源对其他条件下的电场进行建模运算［1-2］.上述问题的难点在于正演模型的建立和场源最优解的计算（超定方程组的求解）.在船舶静电场的建模方面，目前主要有边界元法［3］、有限元法［4］、偶极子源法［5］和电流元法［6］，其中，等效偶极子源和电流元法因相对求解的场源信息较少而被广泛应用于船舶电场的深度换算领域［6-8］.由于船舶静电场可近似为电流元场的叠加［9-10］，考虑到电流元可等效为点电源，提出了基于点电源的船舶静电场反演方法.

1 基于点电源的静电场建模方法

在对船舶静电场进行建模时，可将静电场视为由电荷密度为σ（S）的闭曲面S所产生的，则S在某一场点P处的电位可表示为［11］

式中：γ为海水电导率；K（S，P）为点P与S之间的距离函数.

将表面S分为n个小面源Si，i＝1，2，…，n，每个小面源的电荷密度为σ（Si），则船舶电场真实源在某一场点P处的电位可近似表示为n个等效面源在该点产生电位的和，即

式中：Qi为面源Si上的电荷；ΔSi为等效面源的面积；K（Si，P）为面源Si和场点P之间的距离函数.

由电多极矩的相关知识可知，如果场点P（坐标为（xp，yp，zp））距离等效面源Si区域较远，可将K（Si，P）相对面源Si内的某一点（xi，yi，zi）进行泰勒展开，得

由于在0阶收敛半径之外，可忽略高次项，仅保持第一项［12］，因此，式（2）可表示为

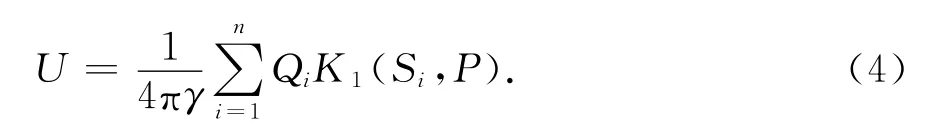
式中，K1（Si，P）为等效点源的坐标（xi，yi，zi）到场点P处的距离函数.

根据式（4）可知，船舶的静电场可等效为n个点源产生的电场和.在利用式（4）进行电场计算时，其核心参数K1（Si，P）在空气-海水-海床三层均匀介质条件下为［13］

式中：H为海水深度；k＝（γ-γ1）／（γ＋γ1）为海底反射系数，γ1为海床电导率；m为反射层数，实际计算中其上限值可取10～20［14］.

值得注意的是，在利用式（4）计算场点P处的电位时，为了减小计算误差，场点与等效点源之间的距离应大于函数K（Si，P）泰勒公式展开时的收敛半径.

有了海水中任意一点的电位表达式（4），便可计算出该点的三分量电场表达式为

式中：

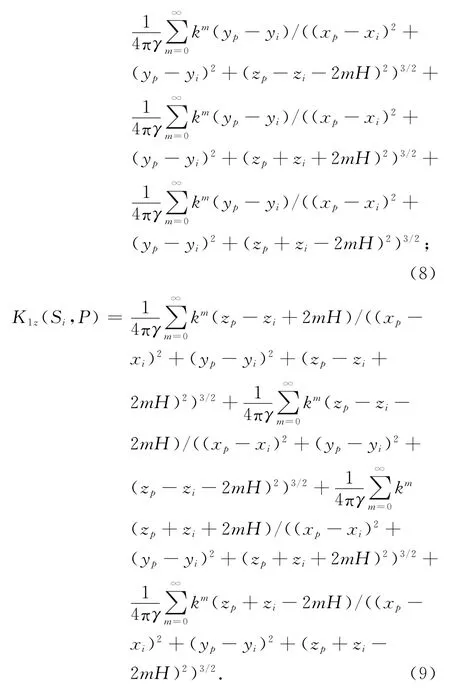
2 基于点电源的静电场反演方法

由第1节分析可知，船舶的静电场可等效为n个点源产生的电场和，因此，在利用点源叠加的方法对静电场进行反演时，需要计算的未知参数主要包括：点源个数n、点源坐标（xi，yi，zi）和点源等效电荷Qi.若能利用先验信息确定点源个数n和点源坐标（xi，yi，zi），则将简化计算量.

2.1 点源位置计算

根据理论计算和实测数据分析可知，船舶静电场电位关于中轴线对称，因此，在反演时可将等效源分布在沿船体纵向方向的平行线上，平行线关于轴对称分布，其数量m可以是任意的偶数（通常取m＝2），每条平行线与船体肋骨横截面的交点即为等效点源的位置.

某一肋骨截面等效点源的位置（m＝2）具体确定方法如下：建立如图1所示的船体坐标系o-xyz，其中，y轴为船体的横向方向，z轴为垂直方向，｜od｜＝B／2（B为船宽）.为了使同一截面上等效点源的位置关于船中轴线对称，将等效点源e和f的坐标分别位于cd和cg的中垂线上是合适的，且e和f关于轴线对称分布，为了保证所有测量点均在泰勒展开的收敛半径之外，应保证由点源e形成并经过c、d和最近测量点s的圆的半径最小.利用以上方法，可方便地求出等效源点e、f的位置.需要说明的是，上述点源位置的确定方法并不是为了对点源进行准确的定位，而是一种满足由式（4）进行等效计算条件下合理点源位置的计算方法.

图1 两条平行线等效源坐标示意图

为了保证换算具有较高的精度，所有测量点应在K（S，P）泰勒公式展开时的收敛半径之外，因此可将最近测量点s与等效点源e之间的距离R视为最大收敛半径，在此条件下，可保证其他测量点均在收敛半径的范围之外.在上述基础之上，根据图2很容易确定点源的最小个数nmin为

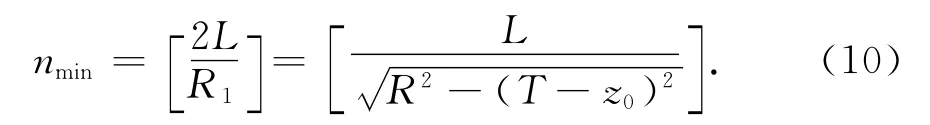
式中：z0为e点的垂直坐标；T为船舶吃水深度；L为船舶水线长度为点源纵向方向的最大间隔；方括号表示选择大于括号里数值的最小偶数.

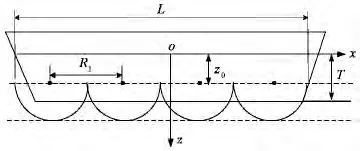
图2 等效源间隔示意图

实际计算过程中，为了提高精度，通常取n稍大于nmin.根据n即可方便地求出等效点源的位置信息：

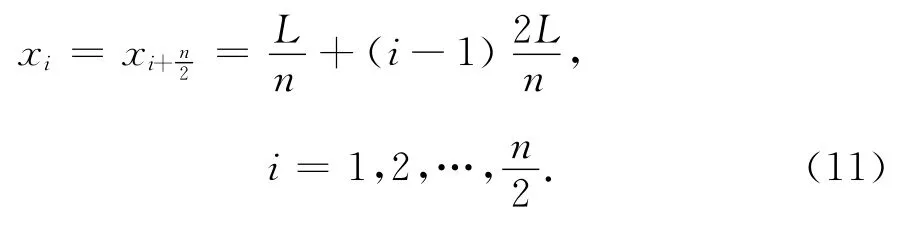
若在实际计算过程中，发现等效点源的位置在船体横截面积以外，将等效源分布在沿船体纵向方向的一条直线（在o-xz平面与中轴线平行）上是合适的，该直线与肋骨截面的交点即为等效点源的位置.与两条平行线点源位置的确定方法类似，此时，只需保证点源形成并经过d、g和最近测量点s的圆的半径最小.为了确保某一深度平面的所有可能的测量点按照式（4）进行计算时，均具有较高的精度，可将过最近测量点s的圆的半径最小转变为点源与最近测量平面相切的问题（如图3所示），得

式中，zh为距e最近的测量点s的深度.当h≤T时，取z0＝h，否则取z0＝T.

取R＝zh-z0，即有

图3 一条平行线等效源坐标示意图

根据式（10）、（11）可计算所需要的最小点源个数及每个点源的位置，由于所有点源在同一条直线上，由式（11）获取的点源位置存在重合现象，但在计算时不影响，为了进一步减小误差，在计算点源个数时，可取R1＝zh-z0

2.2 反演算法

在确定点源个数及其坐标后，可根据式（6）～（9）对测量点建立电场计算模型，假设源点个数为n，点源坐标分别为（xi，yi，zi），i＝1，2，…，n，测量点坐标及其电场值分别为（xj，yj，zj）和（Exj，Eyj，Ezj），j＝1，2，…，m.分别计算每个点源相对于每个测量点之间的距离函数K1x（Si，Pj）、K1y（Si，Pj）和K1z（Si，Pj），则可建立电场方程：

通过方程（14）的求解可得到Qi，在实际测量过程中有m＞n，方程（14）为冗余方程，此时可采用最小二乘法对方程进行求解，即式（14）转化为最小泛函数

的求解.

为了避免超定方程的求解问题，对式（15）增加控制方程，得到

式中，α为控制参数.

同时，式（16）的解应满足电中性方程

利用最小值条件

得到n个方程.联合式（17），得到n＋1个方程，其矩阵表达式为

定 义K1x（Si，Pj）＝ηij、K1y（Si，Pj）＝κij、K1z（Si，Pj）＝λij，则式（19）中的aii、aij、bi为

综上所述，在获得点源个数n、点源坐标（xj，yj，zj）和点源等效电荷Qi之后，便可对其偶极矩进行估算：

同时，可以利用式（6）对任意场点的电场信号进行计算.

3 典型算例

3.1 仿真船舶电场数据

为了检验上述方法的有效性，利用英国研制的Beasy软件（该软件在船舶设计阶段被用于对船舶电场信号进行评估［15］）对某船舶进行电场计算，其中，船舶水线长L＝117m，水线宽B＝15.6m，吃水深度T＝6.27m.船壳的材料为钢，涂有防腐蚀涂层，螺旋桨材料为铜镍铝合金，假设该船舶船身涂层大致完好，但螺旋桨是裸露在海水中的，且船壳某处涂层有破损，螺旋桨和船壳破损区域即是被腐蚀区域.船身上有两对位置对称的辅助阳极，四个辅助阳极的坐标分别为（10.5，-4.9，0.8），（10.5，4.9，0.8），（55，-7，3.69），（55，7，3.69）.船身破损区域和阳极位置如图4中标注所示.三维的船壳模型被离散为1 708个单元，船身的大部分单元为四边形，在船首船尾处有少量单元为三角形，每个分割成的单元可以表示该部分的电压、电流和电流密度等各种信息.

图4 离散后的船壳模型

设海水电导率γ＝4S／m、海底电导率γ1＝0.01S／m，海水深度H＝500m.令两对辅助阳极分别输出-12A和-8A的保护电流，水面以下10 m和20m处的静电场Ex、Ey、Ez和电位分别如图5和图6所示.

从图5中选取200个点作为已知场点，其坐标如表1所示，电场值如图7所示.

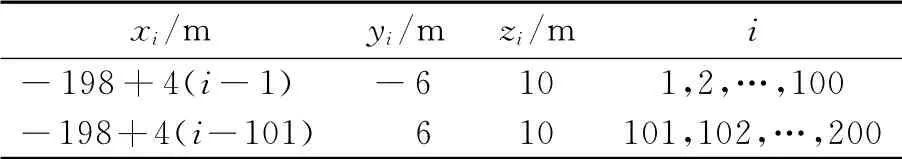
表1 场点坐标

3.2 反演及换算性能检验

根据2.1节中的点源坐标计算方法，可求出e点的位置y0＝-8.10m、z0＝8.343m，y0和z0均在船体横截面积之外.因此，可取y0＝0m，利用式（12）计算得到z0＝1.958m.取R1＝zh-z0＝8.042m，根据式（10）可计算出最小点源个数为nmin＝30，本例中取n＝32，此时可求出等效点源的间隔为R1＝2L／n＝7.32m，从而等效点源的坐标值为

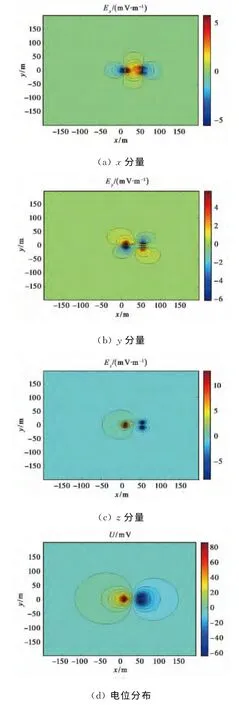
图5 水深10m的电场及电位分布

图6 水深20m的电场及电位分布布

图7 不同正横距下的船舶电场信号

根据式（19）、（20）对静电场建立模型以求解Qi，值得注意的是，式（20）中的α选择对算法的结果影响较大，计算过程中可将α依次选取为α1＝10，αs＝0.1×αs-1，s＝2，3，…，分别计算其等效电荷Qi，并计算sum（Q）＝Q1＋Q2＋…，Qn，若其值在一定范围内接近于0，并且稳定，即可将α取为当前所设定的值.在此算例中，s＝10即α＝10-8时，sum（Q）接近于0，并且稳定.求出Qi后，利用式（21）可计算出Mx＝-1140A·m、My＝0A·m和Mz＝-4.6·10-10A·m.

值得注意的是，模型反演出的点源位置和Qi应与实际船舶电荷分布相近，本例中等效电荷Qi的大小及其分布如图8所示.从图8可明显发现：在10.97m、54.84m分别出现了电荷的极值，与辅助阳极的位置（10m、55m）相符，说明了模型的正确性；但在船壳破损区域处的电荷值不明显，这是由于辅助阳极为点电极，因此在利用点电源进行反演时对其定位精度较高.若适当增加n的个数，对局部破损区域的定位精度有望得到提高.图9是n＝44时反演出的等效电荷大小及其分布.从图9可明显发现，不但在10m和55m附近出现了电荷极值，在20m位置附近，同样出现了电荷的极值，与破损区域的位置相近.

在求出所有的源点信息后，便可对任意场点的电场值进行计算，图10和图11分别为z＝10m时，y＝-10m和y＝10m的实际电场信号和换算结果.图12为z＝20m，y＝-10m时的实际电场信号及换算结果.

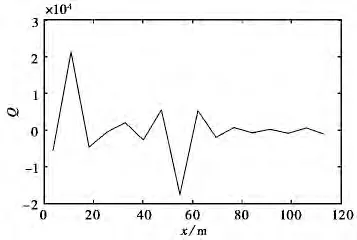
图8 n＝32时等效电荷大小及其分布

图10 z＝10m，y＝-10m时的电场换算及实际结果

从图10～12可明显发现，利用z＝10m正横距为y＝-6m和y＝6m的200个测量点的电场值，向同一深度（z＝10m）、不同正横距（y＝-10 m、y＝10m）和同一正横距（y＝-10m）、不同深度（z＝20m）的场点进行换算时，精度较高，换算结果可近似满足实际的需要.但在辅助阳极位置附近，换算误差明显增大，这是由于辅助阳极位置附近的电场变化剧烈，利用式（5）对电场进行等效计算时误差较大，为了提高计算精度，应适当增加泰勒公式展开的项数.

图11 z＝10m，y＝10m时的电场换算及实际结果

图12 z＝20m，y＝-10m时的电场换算及实际结果

4 结 论

为了对船舶静电场进行反演，提出了基于点电源的船舶静电场深度换算方法，该方法首先利用先验信息对点源的位置进行了确定，避免了以往算法中源位置未知引起的未知参数过多而导致的局部最小解问题，通过仿真数据检验发现，该算法换算效果较好，为船舶静电场反演及换算方法提供了一种新的思路.

［1］林春生，龚沈光.舰船物理场［M］.北京：兵器工业出版社，2007：237-242.

［2］HUBBARD J C，BROOKS S H，TORRRANCE B C.Practical measures for reduction and management of the electro-magnetic signatures of in-service surface ships and submarines［C］／／Underwater Defense Technology Conference，1996：64-65.

［3］ZAMANI N G.Boundary element simulation of the cathodic protection system in a prototype ship［J］.Applied Mathematics and Computation，1988，26：119-123.

［4］DOIG P，FLEWITT P E J.A finite difference numerical analysis of galvanic corrosion［J］.Electrochem，1979，126（12）：2057-2063.

［5］LU Xincheng，CHEN Hunqing，MA Shoujun，et al.The electromagnetic field generated by time-harmonic electric current element in shallow sea［C］／／Undersea Defense Technology Conference.Hamburg，2006.

［6］陈 聪，龚沈光，李定国.舰船静态电场深度换算方法［J］.哈尔滨工程大学学报，2009，30（6）：719-722.CHEN Cong，GONG Shenguang，LI Dingguo.The method of extrapolation of the static electric field of ships［J］.Journal of Harbin Engineering University，2009，30（6）：719-722.（in Chinese）

［7］刘文宝，王向军，稽 斗.基于电偶极子模型的舰船静电场深度换算［J］.空军雷达学院学报，2010，24（6）：436-439.LIU Wenbao，WANG Xiangjun，JI Dou.Conversion of static electric field depth of ships based on electric dipole model［J］.Journal of Air Force Radar Academy，2010，24（6）：436-439.（in Chinese）

［8］陈 聪，李定国，龚沈光.基于拉氏方程的舰船静态电场深度换算［J］.电子学报，2010，38（9）：2025-2029.CHEN Cong，LI Dingguo，GONG Shenguang.Research on the extrapolation of static electric field of ships based on laplace equation［J］.Acta Electronica Sinica，2010，38（9）：2025-2029.（in Chinese）

［9］DYMARKOWSKI K，UCZCIWEK J.The extremely low frequency electromagnetic signature of the electric field of the ship［C］／／Underwater Defense Technology Conference.London，2001：1-6.

［10］BOSTICK F，SMITH H，BOEHL J.The Detection of ULF-ELF Emissions from Moving Ships［R］.New York：State Academic Educational Institutions，1977：13-24.

［11］SUSANU T，LINGVAY I，STOIAN F.The finite differences method to determine the potential function values in the three-dimensional space around a seagoing ship［C／OL］.1991［2013-07-15］.http：／／www.fict.ro／～ep／publications＿files／elecship＿98＿slsp.pdf.

［12］VANDERLINDE J.Classical Electromagnetic Theory［M］.2nd ed.London：Springer，2005：33-35.

［13］JONES D L，BURKE C P.The DC filed components of horizontal and vertical electric dipole sources immersed in three-layered stratified media［J］.Annales Geophysicae，1997，15：503-510.

［14］BANNISTER P.New Formulas for HED，HMD，VED，and VMD Subsurface-to-Subsurface Propagation［R］.USA：Naval Underwater Systems Center，1984：1-38.

［15］ADEY R，BAYNHAM J.Predicting corrosion related electrical and magnetic fields using BEM［C］／／Underwater Defense Technology.Tracey Westwood，2000：386-391.