基于压缩感知的稳健单通道波达方向估计方法

王超宇 梅 湄 李洪涛 朱晓华

（南京理工大学电子工程与光电技术学院，江苏 南京210094）

引 言

近年来，信息论和信号处理领域中提出的压缩感知［1-3］（Compressive Sensing，CS）理论被广泛应用于雷达、图像处理、无线通信和生物医学等诸多工程领域［4］，吸引了研究者们的极大关注.CS理论指出，通过求解一个范数优化问题便可通过少量的非自适应随机测量值以较高精度重构可稀疏表征的信号［5］.

实际空间中感兴趣目标场景的强散射中心仅占据少量的角度分辨单元，照射区域内目标回波信号是稀疏的，由此CS在波达方向（Direction of Arrival，DOA）估计中的应用也得到了广泛的研究.文献［6］提出了基于CS的多输入多输出（Multiple-Input Multiple-Output，MIM）雷达DOA估计方法，充分利用雷达回波信号的稀疏性对阵列接收信号进行时域压缩采样，降低了阵列接收的时域采样点数.文献［7］采用阵元随机分布的天线阵列对空域信号进行压缩采样，降低了接收阵列的前端接收通道个数，随后通过CS重构算法实现DOA高分辨估计.然而，文献［6］和［7］将均匀量化感兴趣区域角度范围得到的超完备基矩阵作为冗余字典，不能保证对应感知矩阵满足约束等容条件（Restricted Isometry Property，RIP）［8］，并且未考虑实际应用中接收阵列射频通道间增益不一致以及感知矩阵和目标角度信息的匹配关系对DOA估计精度的影响，导致目标角度信息估计误差增大.文献［9］从理论上分析了CSDOA中系统模型失配误差对目标角度信息估计精度的影响，结果表明稀疏基矩阵与目标角度信息匹配关系不理想时，常见CS算法对目标信息重构性能劣化非常明显.文献［10］提出一种增加稀疏基矩阵分辨力的方法，降低了系统感知模型失配误差对目标角度信息重构精度的影响，然而随着稀疏基矩阵分辨力的提高，感知矩阵的相关系数亦会随之变大，严重影响了CS重构稀疏信号的精度；此外，当稀疏基矩阵分辨力较高时，感知矩阵规模过大，导致CS重构算法运算量急剧增加.

针对上述问题，本文提出一种单通道CS-DOA估计方法.首先，构建系统感知模型与目标角度信息失配背景下的DOA估计模型；其次，引入一种单通道阵列［11］体制，采用0／π移相器对每个阵元进行随机移相处理，经合路器输出一路数据以完成空域随机采样，克服了射频通道间增益不一致，幅相不平衡等因素对CS-DOA方法的影响；最后，将丹茨格（Dantzig Selector，DS）［12］算法和遗传算法相结合，提出一种新的CS-DOA估计方法，实现系统感知模型失配时的高分辨DOA估计.与CS-DOA估计算法RMFOCUSS［13］相比，本文方法有效降低了系统模型失配误差对DOA估计精度的影响；与传统的CAPON算法和多重信号分类（Multiple Signal Classification，MUSIC）算法相比，本文方法能够对任意相关的信号进行有效估计，具有更高的角度分辨力和更优的估计性能.

1 DOA估计信号模型

1.1 DOA估计压缩感知模型

假设有K个远场窄带信号入射到由L个阵元组成的均匀线性阵列上，考虑噪声干扰时，阵列接收信号可表示为

设感兴趣区域的角度范围Δθ＝［0°，180°］经均匀量化后获得角度网格矢量为＝，N为网格总数，φ＝为角度分辨单元，则式（1）可改写为

式中：s（t）＝［s1（t），…，sN（t）］T是目标角度信息矢量；A）＝［a，…，a）］为角度分辨单元相对接收阵列的导向矢量矩阵.

实际中，照射区域内目标仅占据少量角度分辨单元，即‖s（t）‖0＝K≪N，‖v‖0表示矢量v的l0范数，由此阵列接收信号x（t）为K稀疏信号，为稀疏基矩阵，K为目标角度信息矢量的稀疏度.

1.2 系统感知模型失配时DOA估计模型

假设照射区域内K 个目标相对接收阵列的角度矢量θ＝［θ1，…，θK］中的第k个元素θk，即第k个目标的角度信息与系统预先设定的角度网格矢量不匹配，称系统感知模型与目标角度信息失配.由CS理论可知，系统感知模型失配误差将导致预先设定的角度网格矢量无法准确表示目标场景，造成常见CS-DOA估计方法目标角度信息估计误差变大，角度分辨力降低等问题.

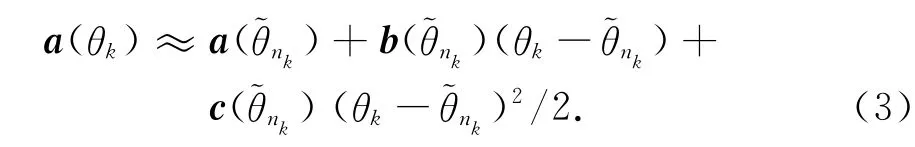
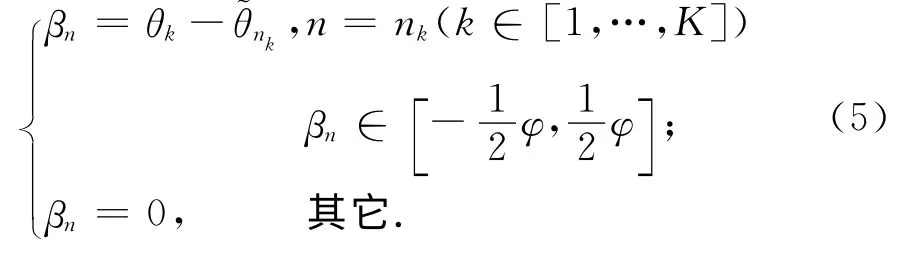
由式（4）可知，当系统感知模型与目标角度信息失配时，Φ为真实导向矢量的二阶近似；当系统感知模型与目标角度信息匹配时，Φ为真实导向矢量的零阶近似，即β＝［0，…，0］T.

因此，不考虑测量噪声的近似误差时，式（2）可近似表示为

1.3 基于单通道阵列的DOA估计模型

由于单通道阵列仅有一个射频通道（如图1所示），故除功耗低、成本低、体积小等优点，还可以有效避免接收阵列通道间增益不一致，幅相不平衡等因素对后续信号处理的影响，具有很强的工程应用价值［11，14-15］.

基于上述特点，本文将单通道阵列体制引入基于CS的DOA估计中.首先，将接收阵列中各阵元均连接一个0／π移相器，通过随机变化各移相器的相位完成对空域的随机采样；其次，利用L路合路器将每个阵元加权后的接收信号合为一路信号输出；最后，经过单路射频通道和A／D转换器后输出数字信号ys（t）：

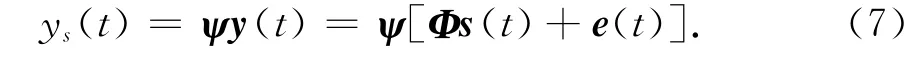
式中，ψ＝［ψ1，…，ψL］为L组0／π移相器随机生成的加权系数矢量，ψi＝cos（0／π）.

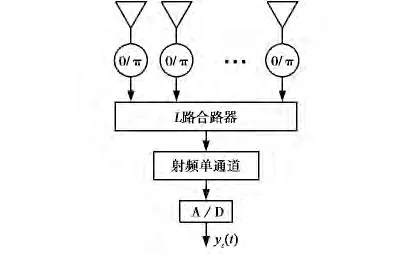
图1 单通道体制阵列模型

由于目标在空间是稀疏的，根据目标信号的时间相关性，设在M个快拍期间目标未跨角度单元移动，即si（t）与sj（t）（i≠j）非零元素位置相同，那么单通道阵列对感兴趣目标场景的M个快拍测量值可表示为

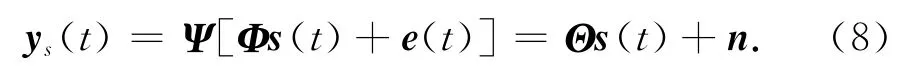
通过分析式（8）不难发现，采用单通道阵列对空间信号进行接收，可看作采用测量矩阵Ψ对回波信号y（t）进行随机投影测量，并且感知矩阵Θ为元素服从伯努利分布的矩阵Ψ与逆傅里叶变换矩阵的乘积，在很大概率上满足RIP条件，保证了采用压缩感知重构算法进行DOA估计的有效性和稳健性.

2 改进的CS-DOA估计算法

基于CS的DOA估计方法主要有MOMP、MORMP以及RMFOCUSS等.一般情况下，即系统感知模型与目标角度信息匹配时，可利用上述方法直接优化求解欠定性方程组获得高分辨DOA估计.在系统感知模型与目标角度信息失配情况下，上述方法无法克服失配误差对DOA估计精度的影响，导致估计误差增大.

针对上述问题，本文提出一种适用于系统感知模型与目标角度信息失配情况下的CS-DOA估计方法.该方法将DS算法和遗传算法相结合对系统感知模型失配误差和目标角度信息交替迭代优化，经过有限次迭代后获得有效的DOA估计结果，具体步骤如下：

步骤1：初始化迭代次数.p＝0.β（p）＝0，［s（t）］（p）＝ΘHys（t）.

步骤2：当迭代至第p＋1次时，经前p次迭代后估计出的各参数分别记为［s（t）］（p）和β（p），则校正后的导向矢量矩阵为

由此，在感知矩阵Θ（p）＝ΨΦ（p）已知的条件下，利用DS算法重构s（t）的结果为

式中μ是与噪声有关的常量，并且当μ＝（1＋η-1）时，s（t）能够以较高的精度进行重构［16］，η为一个正实数，σ为式（8）中噪声n的方差，vmax为Θ（p）中各列2范数的最大值.

需要指出，在低信噪比情况下，DS算法在抑制噪声的同时也损失了部分目标回波信号的能量，使得重构目标信号的幅值有所下降，故本文采用后向投影的方法对DS算法估计结果进行校正：

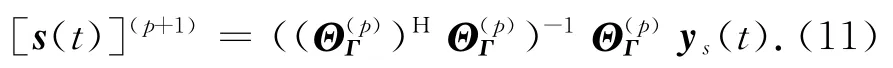
步骤3：当［s（t）］（p＋1）已知时，系统感知模型失配误差β（p＋1）可通过求解一个最优范数问题进行重构：

需要说明，步骤3中最小化式（12）的优化问题是典型的离散非线性多变量优化问题.目前解决此类优化问题的方法有神经网络算法，粒子群优化法（Particle Swarm Optimization，PSO），模拟退火算法（Simulated Annealing，SA）和遗传算法等.其中，神经网络算法通常收敛至局部最小值；PSO早期收敛速度较快，但到了寻优的后期，其收敛速度减慢，且容易收敛到局部极小值；SA较好地解决了寻求最优时陷入局部解的问题，但增加了算法的复杂度；相比之下，遗传算法仿照生物进化和遗传规律，遵循优胜劣汰的自然进化规则，对解空间不同区域的多个点进行搜索，保证了在搜索过程中以最大概率寻找到全局最优解，因此在实际中得到了广泛应用.本文采用遗传算法求解式（12）的具体步骤如下：

步骤1：随机产生若干个系统感知模型失配误差矢量作为遗传算法的初始化群体；

步骤2：以式（12）作为适应度函数，计算每个个体的适应度值；

步骤3：采用“轮盘赌”的方式，根据适应度值来选择优良个体，同时将适应度值最高的个体直接复制到下一代，保证最优个体在遗传过程中不丢失；

步骤4：以设定的交叉概率采用两点交叉方法来产生新个体；

步骤5：以设定的变异概率在交叉后的种群中进行变异产生后代；

步骤6：当完成设定迭代次数或得到数学期望的适应度值时，将最优个体取出并进行译码得到优化后的系统感知模型失配误差，算法结束，否则返回步骤2.

3 计算机仿真及分析

本节分别通过非相干信号和相干信号等信号模型，与传统的CAPON算法、MUSIC算法以及RMFOCUSS算法进行对比，验证本文方法的有效性.仿真中假设接收阵列的阵元个数为L＝16，阵元间距在［0，Lλ／2］范围内均匀分布，阵列接收回波信号快拍数为M＝200，DOA估计均方根误差为

实验1 非相干信号DOA估计.假设角度分辨单元φ＝1°，当信噪比RSN＝0dB，接收阵列各射频通道一致性较好，多个非相干信号相对接收阵列的入射角分别 为［31.5°，37.3°，45.5°，50.2°］时，CAPON、MUSIC、RMFOCUSS算法以及本文方法的空域谱估计归一化输出结果对比如图2所示.不同算法DOA估计的均方根误差随信噪比变化曲线的500次蒙特卡罗实验结果如图3所示.

由图2可以看出：MUSIC算法和CAPON算法无法对目标角度信息进行高分辨估计；RMFOCUSS算法较传统DOA估计方法具有更高的角度分辨力，然而系统感知模型与目标角度信息失配极大影响了该方法DOA估计的精度；相比之下，本文方法根据系统模型失配误差的估计结果对系统感知模型进行了校正，使得DOA估计精度得到了明显的改善.通过对比图3中各算法DOA估计均方根误差随信噪比变化曲线可以看出，在低信噪比条件下，由于本文方法迭代过程中采用后向投影的方式持续对DS估计结果进行修正，提高了低信噪比下CS-DOA方法的适用性，并且通过抑制系统模型失配误差，降低了系统感知模型与目标角度信息失配对DOA估计精度的影响，故较其他几种方法具有更好的估计性能；RMFOCUSS算法稍差，但优于传统的MUSIC和CAPON算法，与图1的结果相一致.

图2 非相干信号的空域谱估计输出

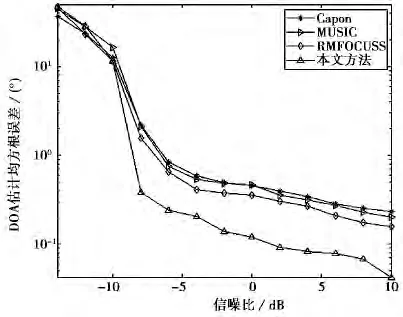
图3 非相干信号DOA估计均方根误差随信噪比变化曲线

实验2 相干信号DOA估计.假设本实验中多个目标的RCS相关，信噪比RSN＝0dB，其他参数设置与实验1中非相干信号DOA估计的参数相同.图4为不同算法的空域谱估计归一化输出结果对比.图5为各算法对相干信号DOA估计均方根误差随信噪比变化曲线的500次蒙特卡罗实验结果对比.从图4可以看出：传统DOA估计的MUSIC算法和CAPON算法在相干信号条件下，性能下降明显，无法对目标角度进行高分辨估计；RMFOCUSS算法在相同条件下DOA估计性能存在一定程度的劣化，但是该算法较传统算法谱估计输出具有更窄的主峰和更低的旁瓣，优于传统DOA估计方法；本文方法通过对系统感知模型进行校正，降低了系统模型失配误差的影响，故较RMFOCUSS算法具有更高的估计精度.对比图5中各算法DOA估计均方根误差随信噪比变化曲线，进一步验证了本文方法在系统感知模型与目标角度信息失配的条件下，具有更高的角度分辨力以及更优的DOA估计性能.

图4 相干信号的空域谱估计输出

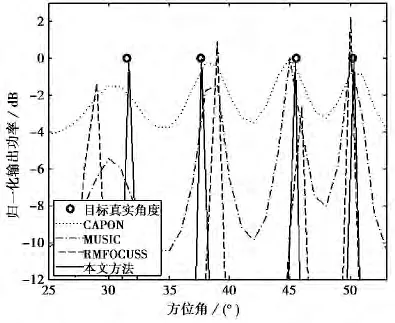
图6 射频通道增益不一致时非相干信号的空域谱估计输出

图7 射频通道增益不一致时非相干信号DOA估计均方根误差随信噪比变化曲线

实验3 射频通道增益不一致时，非相干信号DOA估计.假设本实验多个非相干信号相对接收阵列的入射角与实验1相同，接收阵列射频通道间增益服从均值为1，方差为0.05的复高斯分布.图6为各算法在RSN＝0dB时空域谱估计归一化输出结果对比.图7为不同算法DOA估计均方根误差随信噪比变化关系曲线的500次蒙特卡罗实验结果对比.从图6可以看出：MUSIC算法和CAPON算法在接收阵列通道间增益不一致时已经无法进行有效DOA估计；RMFOCUSS算法虽然较传统DOA方法具有较更高的角度分辨力，但由于无法准确抑制通道间的不同增益和系统模型失配误差的干扰，导致DOA的估计精度下降非常明显；相对而言，本文方法通过引入单通道阵列体制，有效避免了各通道间增益不一致对DOA估计的影响，并且采用改进的DS算法提高了系统模型失配误差存在时目标角度信息的估计精度，保证了DOA估计的有效性.图7中各算法DOA估计均方根误差随信噪比变化曲线也验证了本文方法在接收阵列各射频通道增益不一致以及系统感知模型与目标角度信息失配等背景下，具有更优的DOA估计性能和更好的稳健性.

4 结 论

通过校正系统感知模型改善DOA估计性能是CS-DOA方法研究的一个重要方面，对于有效提高CS在实际中的适用性有着重要的理论和现实意义.本文针对接收阵列射频通道间不一致以及系统感知模型与目标角度信息失配背景下CS-DOA估计性能下降的问题，提出一种单通道阵列体制下的CSDOA估计算法.与常见DOA估计方法相比，该方法有效避免了接收阵列通道间增益不一致，幅相不平衡等因素对DOA估计性能的影响，且通过校正系统感知模型显著降低了目标角度信息的估计误差.本文方法改善了多目标波达方向的估计性能，增强了CS-DOA的有效性和稳健性，具有较强的工程应用价值.

［1］JULIO M，CUO S，LAWRENCE C，et al.Task-driven adaptive statistical compressive sensing of Gaussian mixture models［J］.IEEE Transactions on Signal Processing，2013，61（3）：585-600.

［2］朱 丰，张 群，顾福飞，等.合成孔径雷达运动目标谱图二维压缩与重构方法［J］.电波科学学报，2012，27（1）：157-164.ZHU Feng，ZHANG Qun，GU Fufei，et al.Two dimensional SAR moving target spectrogram compressive and reconstruction method［J］.Chinese Journal of Radio Science，2012，27（1）：157-164.（in Chinese）

［3］张顺生，常俊飞，李 晶.方位多波束合成孔径雷达压缩感知成像研究［J］.电波科学学报，2012，27（5）：979-984.ZHANG Shunsheng，CHANG Junfei，LI Jing.Compressed sensing for multiple azimuth beams SAR imaging［J］.Chinese Journal of Radio Science，2012，27（5）：979-984.（in Chinese）

［4］LI G，ZHU Z，YANG D，et al.On projection matrix optimization for compressive sensing systems［J］.IEEE Transactions on Signal Processing，2013，61（11）：2887-2898.

［5］JULIAN W，SIMON H，MARTIN K.Analysis based blind compressive sensing［J］.IEEE Signal Processing Letters，2013，20（5）：491-494.

［6］YU Y，PETROPULU A P，POOR H V.MIMO radar using compressive sampling［J］.IEEE Journal of Selected Topic in Signal Processing，2010，4（1）：146-163.

［7］BILIK I.Spatial compressive sensing for direction-ofarrival estimation of multiple sources using dynamic sensor arrays［J］.IEEE Transactions on Aerospace and Electronic System，2011，47（3）：1757-1769.

［8］LIU Z，WEI X，LI X.Aliasing-free moving target detection in random pulse repetition interval radar based on compressed sensing［J］.IEEE Sensor Journal，2013，13（7）：2523-2534.

［9］ALI C G，VOLKAN C，JAMES H M.Bearing estimation via spatial sparsity using compressive sensing［J］.IEEE Transactions on Aerospace and Electronic Systems，2012，48（2）：1358-1369.

［10］CHAE D H，SADEGHI P，KENNEDY R A.Effects of basis-mismatch in compressive sampling of continuous sinusoidal signals［C］／／ICFCC.Canberra，May 2010：739-743.

［11］NURUL H N，TUGHRUL A，BRIAN W F，et al.Single-port beamforming algorithm for 3-faceted pahsed array antenna［J］.IEEE Antennas and Wireless Propagation Letters，2013，12：813-816.

［12］CAI T T，ZHANG A.Compressed sensing and affine rank minimization under restricted isometry［J］.IEEE Transactions on Signal Processing，2013，61（13）：3279-3290.

［13］COTTER S F，RAO B D，ENGAN K，et al.Sparse solution to linear inverse problems with multiple measurement vectors［J］.IEEE Transactions on Signal Processing，2005，53（7）：2477-2488.

［14］IUPIKOV O A，MAASKANT R，IVASHINA M.Towards the understanding of the interaction effects between reflector antennas and phased array feeds［C］／／ICEAA.Cape Town，Sept 2012：792-795.

［15］李洪涛，贺亚鹏，肖 瑶，等.基于压缩感知的单通道鲁棒自适应波束形成算法［J］.电子与信息学报，2012，34（10）：2421-2426.LI Hongtao，HE Yapeng，XIAO Yao，et al.Compressive sensing based single-channel robust adaptive beamforming algorithm［J］.Journal of Electronics ＆Information Technology，2012，34（10）：2421-2426.（in Chinese）

［16］CANDES E J，TAO T.The Dantzig selector：statistical estimation when p is much larger than n［J］.Annals of Statistics，2007，35（6）：2313-2351.