虚拟阵元应用于平板端射天线的新型组阵方法研究

汪月清， 刘姜玲 王小谟 薛正辉

（1.北京理工大学信息与电子学院，北京100081；2.中国电子科学研究院，北京100041）

引 言

端射天线以其体积小、重量轻、低空阻等性能适用于现代高速载体.然而平板端射天线单元存在增益极限，为了满足雷达天线高增益的工程需求，必须将端射天线组阵以获得更高的增益［1-2］.常规端射天线由于本身复杂的耦合关系，导致组阵时得不到预期增益提高，拉大侧向阵元间距为1.5λ时可解决互耦问题获得高增益［3］，但拉大侧向间距组阵会导致栅瓣电平，一般利用不均匀优化布阵来抑制栅瓣.

当天线单元最小间距为1.5λ时，按常规不均匀阵列优化原理优化天线间距，可以抑制栅瓣，但在天线单元数量有限时无法解决引入的高旁瓣电平问题.采用空间不合成组阵原理虽然能够在抑制栅瓣的同时解决高旁瓣电平的问题，但是要以收发分置为前提，并且在工程应用中通过优化改变阵元位置并不现实［4］.

文中提出的数字虚拟端射组阵方法是在大间距的平板端射阵列各单元间内插虚拟阵元来组阵，由于内插虚拟端射天线单元可实现等效的小间距组阵，抑制了栅瓣电平，同时由于虚拟端射天线单元间无互耦，避免了实际端射天线单元间距减小造成的有害互耦导致的高副瓣电平，达到了抑制栅瓣、降低高副瓣电平的目的，从而得到了一种新型高增益端射阵列形式.

1 端射天线栅瓣问题描述

对于一般线阵，当阵元间距小于半波长时，少于一个周期的阵因子在±90°可见空间出现.而当阵元间距大于半波长时，多于一个周期的阵因子在±90°可见空间出现，这时在可见空间中可能不止出现一个主瓣，这种与主瓣强度相等的其余波瓣称为栅瓣［5-6］.栅瓣会造成观测的多值性，因此需要加以抑制.

文中所讨论的端射天线单元包括一个150mm×28mm×5mm金属底板，5根金属振子，长度分别为24.0、21.5、19.0、18.3、18.0mm，振子半径为2mm，振子间距20mm，中心频率为3.2GHz.在组阵实验中，考虑将平板端射天线单元沿侧射方向的组阵情况，以下简称为侧向组阵.4个实际端射天线单元（1、2、3、4）结构一样，侧向组阵间距dy＝1.5λ.由方向图乘积定理

图1 栅瓣产生机理

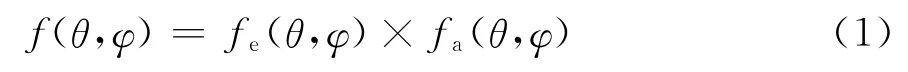
可知，天线阵的H面方向图会出现栅瓣，如图1所示.式（1）中θ为俯仰角，φ为方位角，fe为单元因子，fa为阵因子.而在天线组阵及阵列扫描中，不期望出现栅瓣现象，下面通过内插虚拟阵元的组阵方法进行栅瓣抑制.

2 内插虚拟阵元的组阵方法

内插虚拟阵元的组阵方法是在平板端射天线阵列的实际阵元间插入虚拟阵元，由实际阵元接收到的回波信号计算内插的虚拟阵元接收到的回波信号，将各路回波信号同相叠加形成波束.单条线阵内插虚拟阵元的原理图如图2所示，内插虚拟阵元数由1增加至3，以探究虚拟阵元数目对抑制栅瓣的影响.

图2 虚拟端射天线阵原理图

以第1个实际阵元为参考阵元，阵元之间的延迟可以用相移来等效地表示，那么频率为fc的实际回波信号x（t）的解析表达式为［7］

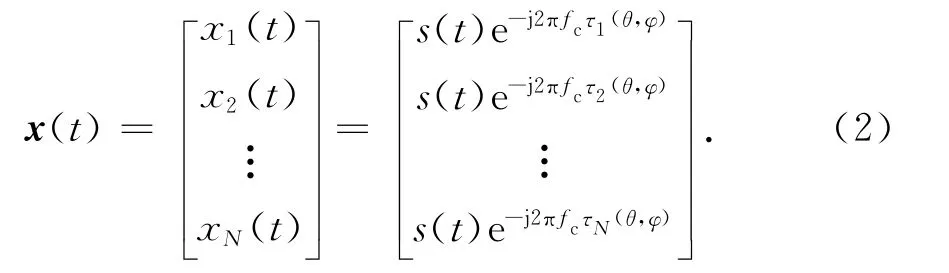
式中：xj（t）为第j路实际回波信号，j＝1，2，…，N，N为 实 际 阵 元 个 数；s（t）为 入 射 信 号；τj＝-（j-1）dysinθsinφ／c为信号到达阵元的时延，c为光速；e-j2πfcτj（θ，φ）为各路回波信号的相位信息.

考虑方位面方向图，θ＝90°，-180°≤φ≤180°，那么实际回波信号叠加后的表达式为

由实际回波信号计算所得虚拟阵元的回波信号为

式中：NXN为虚拟阵元总数；τXNi＝-dXNisin（θ）sin（φ）／c，dXNi为每个虚拟阵元与参考阵元的间距.由此得到虚拟阵未归一化的方向图F为

式中，K＝F1max／（F1max＋F2max）为修正系数，F1max、F2max分别为实际阵列回波信号和虚拟阵列回波信号的峰值电平.由于天线口径和输入功率不变，内插虚拟阵元并不改变实际天线阵的增益，因此，要对同相叠加后的回波信号乘以修正系数以保持增益不变.

3 仿真及实验结果分析

本节给出侧向组阵内插虚拟阵元的组阵结果与实际阵列的CST仿真结果对比.当每两个阵元间均匀内插1个虚拟阵元，dy＝0.75λ时，对比结果如图3所示；当每两个阵元间均匀内插2个虚拟阵元，dy＝0.5λ，对比结果如图4所示；每两个阵元间均匀内插3个虚拟阵元，dy＝0.375λ，对比结果如图5所示.

由图3～5可知：侧向组阵时内插虚拟阵元数越多，阵元间距越小，H面栅瓣越低，但对E面没有影响；内插9个虚拟阵元时，H面方向图栅瓣降低约18dB.

图3 实际阵列与共内插3个虚拟阵元的阵列对比

图4 实际阵列与共内插6个虚拟阵元的阵列对比

图5 实际阵列与共内插9个虚拟阵元的阵列对比

利用作者所在课题组研制的数字端射阵列原理样机开展验证测试，如图6所示.该阵列包括4个发射端射子阵列，8个接收端射天线单元，一个步进频射频信号发射机和接收机，一个幅相校正模块和一个波束形成模块.本实验中发射采用1路发射，接收单元1至4同时接收得到4路回波信号，然后按阵列布置规律（图2）依次获得虚拟单元独立存在时的回波信号测试值，再对各路回波信号经过通道幅相校正后再补偿收发路径相移求和，获得实测虚拟阵列方向图，并与对应的虚拟阵列计算所得方向图结果进行对比.

图6 实验测试布置图

将三种情况计算所得虚拟阵的方向图与实际端射阵测试方向图对比，如图7所示，栅瓣随内插虚拟阵元数的增加而降低，内插9个虚拟阵元时比实际端射阵的栅瓣降低了21dB.

将三种情况测试所得虚拟阵的方向图与实际端射阵测试方向图对比，如图8所示，随着内插虚拟阵元数的增加，栅瓣越来越低，内插9个虚拟阵元时实际端射阵的栅瓣降低了11dB.图8实验测试结果与图7计算结果趋势一致，证明内插虚拟阵元抑制栅瓣的方法是可行的.

图7 实际阵列测试方向图与虚拟阵列计算结果对比

图8 实际阵列与虚拟阵列测试方向图对比

图9为内插9个虚拟阵元时，虚拟阵列方向图实测结果与计算结果的对比.由图9可以更直观地看出虚拟阵列实测结果与计算结果基本吻合.

由实验数据计算所得栅瓣电平与实际测试所得栅瓣电平变化见表1.H面栅瓣电平随内插虚拟阵元数目的增加而降低，降幅趋于平缓.

由以上研究分析，内插虚拟端射天线单元实现了等效的小间距组阵，抑制了栅瓣电平.并且虚拟阵元实际是不存在的，因此虚拟端射天线单元间无互耦，避免了实际端射天线单元间距减小造成的有害互耦导致的高副瓣电平.同时天线口径和输入功率不变使得阵列增益不变.因此，数字虚拟端射组阵方法在保证端射组阵增益不变的同时抑制了栅瓣并降低了副瓣电平.

图9 内插9个虚拟阵元虚拟阵实验结果与计算结果对比

表1 内插虚拟阵元个数不同时的栅瓣电平变化情况

由于受限于数字端射阵列规模，只开展了5振子单元1×4侧向组阵时虚拟阵元的验证实验，后续8×8小规模虚拟端射阵的实验正在进行中.基于以上研究结论我们提出：通过优化虚拟阵元内插位置以及激励的幅度和相位，可以在内插阵元数相同的基础上得到更优的方向图.这一设想需进一步验证.

4 结 论

端射天线单元存在增益极限，为了满足雷达天线高增益的工程需求，必须将端射天线组阵以获得更高的增益.常规端射天线由于本身复杂的耦合关系，导致组阵时得不到预期增益提高，拉大侧向阵元间距可解决互耦问题，获得高增益，但会导致栅瓣电平.本文提出的内插虚拟阵元的组阵方法避免了小间距组阵的复杂互耦并解决了大间距组阵时的栅瓣电平问题，在获得高增益的同时抑制栅瓣并降低副瓣电平，提供了一种在实现低剖面、易共形的前提下也能实现高增益、低副瓣的数字虚拟端射阵列天线组阵方法，为实现端射阵列的工程应用奠定了基础.

［1］YAO Guowei，XUE Zhenghui，LI Weiming，et al.Research on a new kind of high directivity end-fire antenna array［J］.Progress in Electromagnetics Research B，2011，33：135-151.

［2］姚国伟，薛正辉，李伟明，等.平板端射天线组阵的研究［J］.电波科学学报，2009，24（2）：323-326.YAO Guowei，XUE Zhenghui，LI Weiming，et al.The research of plate end-fire antenna［J］.Chinese Journal of Radio Science，2009，24（2）：323-326.（in Chinese）

［3］姚国伟，薛正辉，李伟明，等.增强端射天线阵列的研究［J］.电波科学学报，2010，25（3）：538-542.YAO Guowei，XUE Zhenghui，LI Weiming，et al.Research on enhance directivity of end-fire array［J］.Chinese Journal of Radio Science，2010，25（3）：538-542.（in Chinese）

［4］刘姜玲，刘姜涛，王小谟.空间不合成平板端射阵列副瓣研究［J］.电波科学学报，2011，26（2）：233-237.LIU Jiangling，LIU Jiangtao，WANG Xiaomo.Sidelobe level of flat end-fire antenna powered by uncorrelated signal［J］.Chinese Journal of Radio Science，2011，26（2）：233-237.（in Chinese）

［5］ELLIOTT R S.Antenna Theory and Design［M］.John Wiley ＆Sons，2003.

［6］LIU Lei，CALOZ C，LTOH T.Dominant mode leakywave antenna with backfire-to-endfire scanning capability［J］.Electronics Letters，2002，11（38）：1414-1416.

［7］陆建明.基于最小二乘虚拟阵元的解模糊方法［J］.电子科技，2009，22（11）：9-11.LU Jianming.Fuzzy solution based on least squares virtual array algorithm［J］.Electronic Science and Technology，2009，22（11）：9-11.（in Chinese）