单轴各向异性球对任意方向入射平面波的散射

李正军 吴振森 屈 檀 白 璐 曹运华

（西安电子科技大学 物理与光电工程学院院，陕西 西安710071）

引 言

由于各向异性材料在集成光学、微波、毫米波技术以及隐身技术、装甲技术上被广泛采用，近年来电磁波与各向异性材料之间的相互作用逐渐引起了人们广泛的关注.

目前有许多数值方法和解析方法研究各向异性介质的散射问题.数值方法有时域有限差分（Finite Difference Time Domain，FDTD）法、离散偶极子（Discreted Dipole Approximatien，DDA）法、积分微分方程法、矩量法、T矩阵法［1］等.国内朱秀芹等人［2］采用矩量法-共轭梯度-快速傅里叶变换（method of moment-conjugate gradient method-fast Fourier transform，MOM-CGM-FFT）的混合技术研究了三维均匀介质与非均匀介质目标的散射问题，给出了几种均匀介质的数值计算结果.由于各向异性材料的介电常数和磁导率的特殊性，目前研究各向异性介质球的解析方法比较多样.20世纪80年代中，Monzon［3］采用解析方法研究了电和磁均各向异性的三维结构球和圆柱结构的散射.1992年，Wong等人［4］采用标量特征函数的展开方法研究了有耗单轴异性介质球对平面波的电磁散射；2007年，Qiu等人［5］也采用标量特征函数的展开方法研究了单轴各向异性介质球对平面波的散射.利用微积分理论，Brian［6-7］推导了单个任意形状各向异性介质目标的电磁散射的解析解.1993年，任伟［8］通过引入傅里叶变换，采用特征波函数首次推导了各向异性等离子体球的电磁散射问题.基于其工作，耿友林等人［9］通过引入电磁场的傅里叶变换给出了单轴各向异性球的内场的球矢量波函数展开形式，研究单轴各向异性介质球对平面波的散射.

上述方法主要研究了入射波与主光轴平行时的单轴各向异性球形粒子的散射特性.但是由于单轴各向异性粒子存在主光轴，当入射平面波与主光轴不平行，其内部电磁场是完全不相同的，其散射特性也会有所不同.本文研究单轴各向异性介质球对任意方向入射平面波的散射解析解，数值分析其散射特性.在本文的讨论中，设定时谐因子为e-jωt，其中ω为角频率.

1 理论公式

如图1所示，任意方向传播的平面波入射到半径为a的单轴各向异性介质球上，其中虚线为单轴各向异性介质球的主光轴.假定单轴各向异性介质球的主光轴与z轴一致，Oxyz是以球心O为原点所建立的粒子坐标系.

图1所示平面波的波矢量k0在Oxyz直角坐标系下表达式为

式中：α为入射角，也就是平面波的传播方向与z轴的夹角；β为方位角，也就是平面波的传播方向在xOy平面上的投影与x轴的夹角.

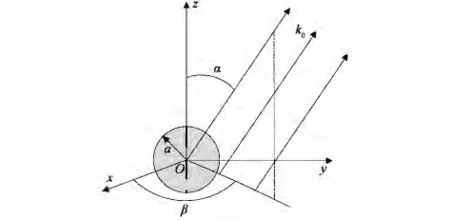
图1 任意方向传播平面波入射到单轴各向异性介质球上

对于任意方向传播平面波同样也有两种极化模式，即TM极化模式和TE极化模式.对于TM极化模式的平面波来说，其电场可以表示为

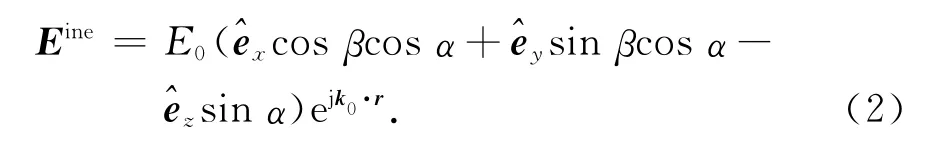
式中：E0是振幅；r是位矢，上标inc代表入射场，而对于TE极化模式的平面波来说，其电场可以表示为

则入射场可在全局坐标系Oxyz下，用球矢量波函数展开为

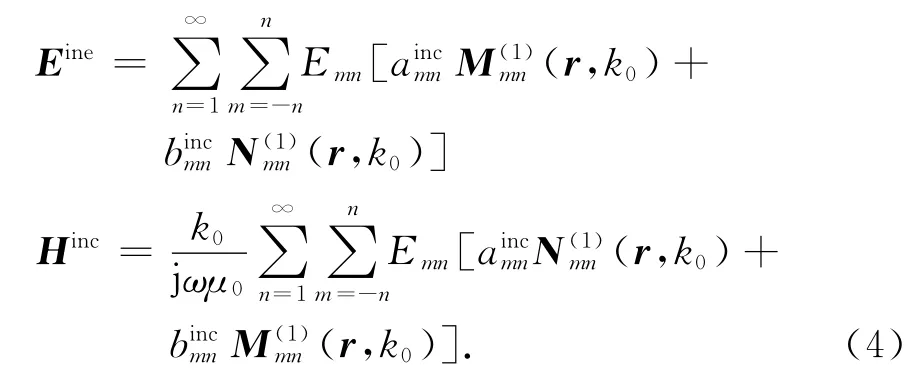
式中：k0＝2π／λ，λ为周围介质中的入射波长；μ0为周围空间的磁导；M（1）mn和N（1）mn为球矢量波函数［10］，其中l＝1，2，3，4分别代表四类球贝塞尔波函数.归一化系数Emn被定义为

因为仅仅考虑两种极化模式任意方向传播的平面波，也就是传播方向和极化方向始终是垂直的，根据球矢量波函数的正交完备性，可求得入射场的展开系数［11］.

对于单轴各向异性介质，电位移矢量D和电场强度E方向，磁感应强度B和磁场强度H的方向不再是简单的平行关系.此时介电常数与磁导率需要用张量形式表示，本构关系变为

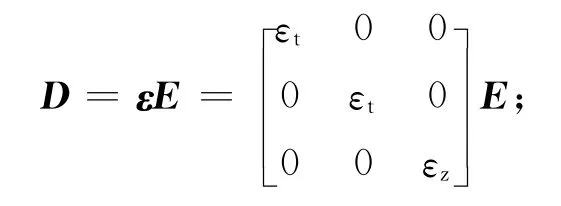
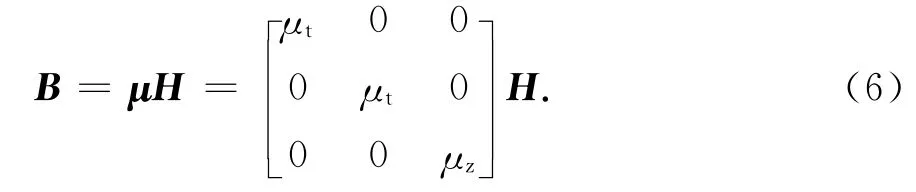
则单轴各向异性介质中的电场矢量波动方程变为

该波动方程由于μ和ε是张量，电场的各个分量是耦合在一起的，无法直接用分离变量法来求解，通过引入Fourier变换，可将内场用球矢量波函数展开为［9］

散射场也可以在粒子坐标系Oxyz下用球矢量波函数展开为

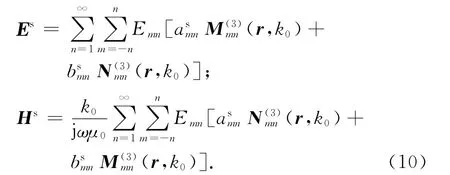
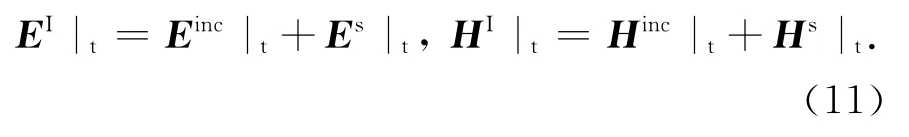
将球矢量波函数的具体表述式代入入射场、散射场及内场中求得其分量，代入式（11）可得到关于散射系数的方程组，解方程组最终可求得散射系数［12］.

求得了单轴各向异性介质球的内部和外部的电磁场，根据雷达散射截面在远区的定义可计算散射特性：

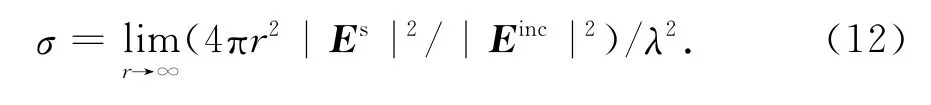
2 数值计算和讨论

如图2所示，分别计算了三种不同传播方向平面波入射情形下，单轴各向异性介质球在E面和H面上的雷达散射截面的角分布，同时给出了用三维电磁场仿真软件（CST）数值模拟这三种情形下的散射结果.在E面和H面上的解析结果与CST数值模拟结果都吻合得很好，从而说明文章任意方向入射平面波的展开方法及对单轴各向异性介质球的散射理论及程序的正确性.当平面波入射方向不再平行单轴各向异性介质球的主光轴时，从图2可以看出，其雷达散射截面不再完全以θ＝180°两边对称，所以需要计算散射角从0°变化到360°的情形.

在图2（a）中，当方位角β＝0°时，平面波极化在xOz平面上，所以入射角为α＝0°与α＝30°两种情形平面波入射下的雷达散射截面的最大值均出现在前向方向上，即出现在波的传播方向上.而由于α＝30°时，平面波的入射方向与单轴各向异性介质球的主光轴不一致，所以雷达散射截面的角分布不仅不再以θ＝180°两边对称，且也与α＝0°时的雷达散射截面的角分布有很大的不同，并不是进行了简单的平移，在θ＝276°时，出现了极小值，几乎达到-35dB.H面上，当方位角β＝0°时，由于此时由平面波的入射方向和极化方向组成的入射平面与观察面垂直，所以可以看到入射角为α＝0°与α＝30°两种情形平面波入射下的雷达散射截面的角分布均是以θ＝180°两边对称的，但是α＝30°时雷达散射截面的大小及角分布与α＝0°时雷达散射截面相比改变得很大.当α＝30°，β＝30°时，由于此时由平面波的入射方向和极化方向组成的入射平面均不与E面和H面垂直或平行，所以其雷达散射截面最大值并非出现在前向方向上，且其角分布也不以θ＝180°两边对称.

图2 雷达散射截面的角分布并与CST结果比较

如图3所示，分别计算了不同介电常数张量元单轴电和磁均各向异性介质球对入射角为α＝45°平面波散射的雷达散射截面在E面和H面上的角分布.可以看出，当单轴各向异性介质球电磁均各向异性时，改变介电常数张量元εz，其雷达散射截面的角分布的震荡周期与大小都会改变，H面的这种改变要比E面的激烈得多，前向雷达散射截面的大小也会随εz改变而改变.当εt＝εz时，单轴各向异性介质球呈现电各向同性，但是磁导率还是各向异性的，所以雷达散射截面的角分布并没有正入射时的对称现象.比如说当εt＝εz＝3时，E面上θ＝225°两边的雷达散射截面的波谷明显不相同.从E面和H面上的雷达散射截面的角分布可以看出εt的改变比εz的改变要对雷达散射截面的影响大.

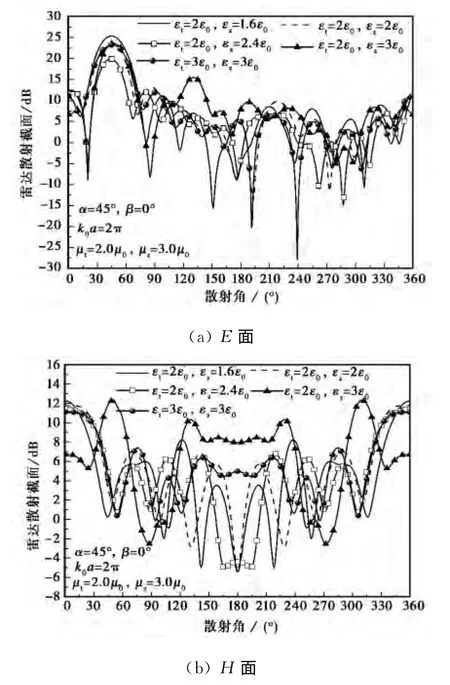
图3 介电常数张量元对雷达散射截面的影响

如图4所示，分别计算了平面波斜入射时不同尺寸参数下单轴各向异性介质球的介电常数张量元与磁导率张量元均为有耗和无耗时的雷达散射截面在E面和H面上的角分布.图中符号A，B，C和D分别表示εt，εz，μt和μz的虚部；无耗表示各向异性介质球为无耗的，即A＝B＝C＝D＝0；有耗表示各向异性介质球为有耗的，即A＝B＝C＝D＝0.5.可以看出，对于无耗介质球，尺寸参数增大时，其雷达散射截面角分布的震荡变得更密集，但是震荡幅度有所变小，这点H面上雷达散射截面的角分布表现得更为明显.对比有耗和无耗的情况，可以发现E面上，是否有耗并不影响雷达散射截面的最大值出现的位置，都是在波的传播方向上，但是会改变雷达散射截面的大小及角分布；可以明显看出有耗时后向部分的雷达散射截面要比无耗时的小；有耗时雷达散射截面的角分布震荡周期及幅度也比无耗小得多，而且这种变化随着尺寸参数的增加变得越来越明显，如H面上，k0a＝4π时，有耗时的雷达散射截面几乎没有震荡.

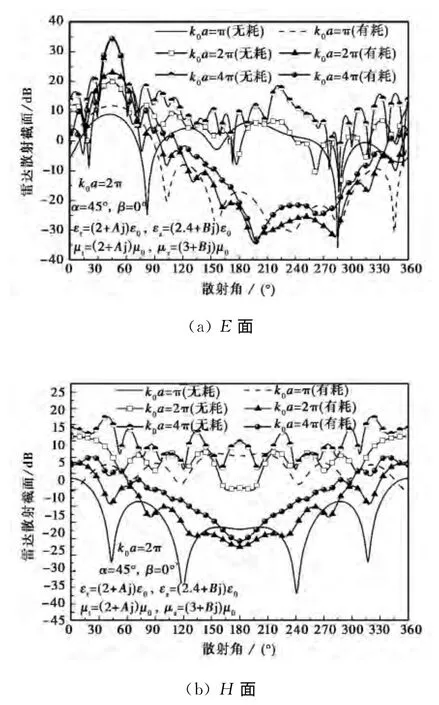
图4 尺寸参数对雷达散射截面的角分布

3 结 论

导出了具有任意传播方向两种极化模式的平面波用球矢量波函数的展开形式，给出了展开系数的具体表达式.研究了单轴各向异性介质球对任意方向入射平面波的散射；与CST数值仿真结果进行比较验证了本文理论及程序的正确性.数值分析了介电常数张量元、有耗、无耗、尺寸参数、入射角和方位角等对单轴各向异性介质球的雷达散射截面的影响.虽然仅仅数值计算了TM极化模式平面波入射情况，对TE极化模式平面波入射时，只需要将TM极化模式入射场展开系数改为TE极化模式入射场展开系数就可计算出其结果来.

［1］BRIAN S，MICHEL N，EVGENY P.T matrix of the homogeneous anisotropic sphere：applications to orientation-averaged resonant scattering［J］.J Opt Soc Am A，2007，24（4）：1120-1130.

［2］朱秀芹，耿友林，吴信宝，等.三维介质目标电磁散射的一种计算方法［J］.电波科学学报，2000，15（4）：397-401.ZHU Xiuqin，GENG Youlin，WU Xinbao，et al.The application of a mixed technique to 3Ddielectric objects［J］Chinese Journal of Radio Science，2000，15（4）：397-401.

［3］MONZON J C.Three-dimensional field expansion in the most general rotationally symmetric anisotropic material：application to scattering by a sphere［J］IEEE Trans Antennas Propagat，1989，37：728-735.

［4］WONG K L，CHEN H T.Electromagnetic scattering by a uniaxially anisotropic sphere［J］.IEE Proceedings-H，1992，139（4）：314-318.

［5］QIU C W，LI L W，YEO T S.Scattering by rotationally symmetric anisotropic spheres：Potential formulation and parametric studies［J］.Phys Rev E，2007，75：026609.

［6］BRIAN S，MICHEL N，EVGENY P.Mie scattering by an anisotropic object part I homogeneous sphere［J］.J Opt Soc Am A，2006，23（5）：1111-1123.

［7］BRIAN S，MICHEL N，EVGENY P.Mie scattering by an anisotropic object Part II Arbitrary-shaped object：differential theory［J］.J Opt Soc Am A，2006，23（5）：1124-1134.

［8］REN W.Contributions to the electromagnetic wave theory of bounded homogeneous anisotropic media［J］Phys Rev E，1993，47（1），664-673.

［9］GENG Y L，WU X B，LI L W.Mie scattering by a uniaxial anisotropic sphere［J］.Phys Rev E，2004，70：056609.

［10］LI Z J，WU Z S.Arbitrary direction incident Gaussian beam scattering by multispheres［J］.Chin Phys B，2011，20（8）：081101.

［11］LI Z J，WU Z S，SHI Y E，et al.Multiple scattering of electromagnetic waves by an aggregate of uniaxial anisotropic spheres［J］.J Opt Soc Am A，2012，29（1）：22-31.

［12］LI Z J，WU Z S，LI H Y.Analysis of electromagnetic scattering by uniaxial anisotropic bispheres［J］.J Opt Soc Am A，2011，28（2）：118-125.