车载雷达稳定转台伺服控制系统仿真研究

冯瑗瑗 丁 锋

（1.中国船舶重工集团公司第七二四研究所，江苏 南京210003；2.东南大学自动化学院，江苏 南京210096）

0 引言

随着科学的发展和技术的进步，雷达已经在军事和民生等方面得到了广泛的应用。其中，车载雷达由于其灵活便捷的移动方式，应用更为普遍，展现出了巨大的潜力。

车载稳定转台为安装在车辆上的雷达天线提供了一个不受车辆运动影响的机械传动转台，它可以在车辆出现倾斜或转向时，使天线始终保持某个固定的倾角和方向，保证雷达正常工作。随着雷达技术的发展，车载雷达对稳定转台伺服控制系统也提出了更高的要求［1］。

本文利用滑模变结构控制不需对系统内部参数和干扰量进行精确观测的特点，设计了基于滑模变结构控制的车载雷达稳定转台伺服系统，并通过与PID控制的对比证明了其优越性。

1 控制对象的机理模型

本文所讨论车载雷达采用两轴稳定转台，天线目标给定角度分为方位角度和俯仰角度，在不考虑方位环与俯仰环之间耦合的前提下，方位伺服电机和俯仰伺服电机分别控制天线转台在方位和俯仰2个自由度上转动，共同作用使天线指向预定方向。以方位控制为例，建立稳定转台方位控制系统数学模型。

考虑稳定转台的控制精度，对伺服系统建立三质量数学模型，即由电机、纯惯性负载以及连接二者的等效传递轴组成，其组合模型如图1所示。

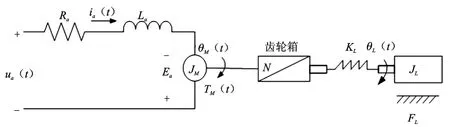
图1 电机通过弹性轴驱动负载的组合模型

利用电机学和自动控制理论的相关知识列出方程：

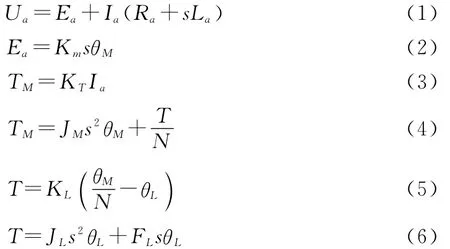
式中，Ua为加在电机电枢两端的电压；Ea为电机反电动势；Ia为电枢电流；Ra为电机的电枢电阻；s为复频域变量符号；La为电机的电枢电感；Km为电机反电动势系数；θM为电机轴的角位移；TM为电机力矩；KT为电机力矩常数；JM为电机电枢转动惯量；T为弹性轴中的力矩（即作用于负载上的力矩）；N为齿轮箱减速比；KL为弹性轴的刚性；θL为传动架的角位移；JL为负载惯量；FL为黏性摩擦常数。

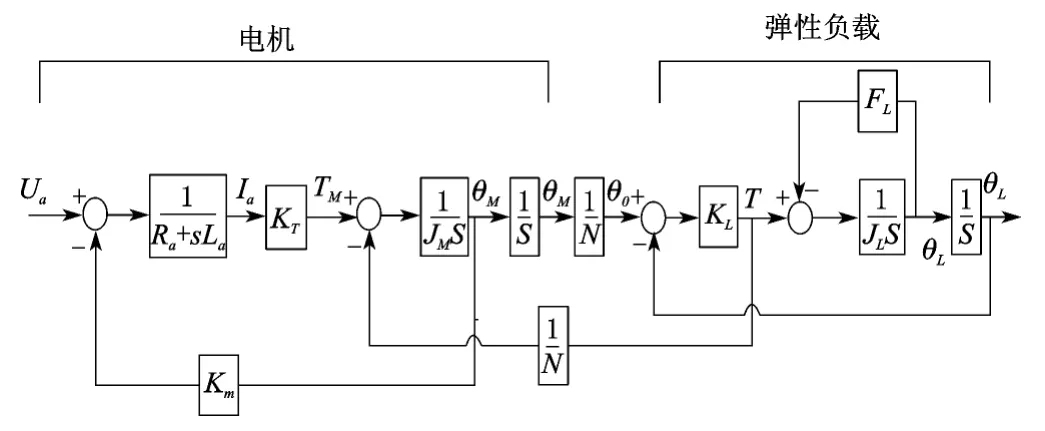
图2 系统模型的方框图

设系统控制参数为：Ra＝2.48Ω，La＝0.038H，JM＝0.0114kg·m2，Km＝0.489V／rad·s－1，KT＝0.898N·m／A，N＝309，KL＝40000N·m／r，JL＝150kg·m2。

伺服控制常用的控制方法是PID控制，一般采用位置—速度双环控制。经过参数寻优，取得较理想的阶跃响应曲线，如图3所示。可以看出，在对被控对象进行精确建模的情况下，PID控制能够取得较为理想的控制效果。

2 稳定转台伺服系统的摩擦模型

本文采用一种比较典型的摩擦模型——Stribeck摩擦模型，它反映了不同摩擦阶段摩擦力矩与速度之间的关系。在不同阶段，接触面之间的相对运动速度是不同的，因此在稳态时摩擦力表现为相对速度的函数［2］，可以通过下列方程进行数学描述：

图3 PID控制位置阶跃响应曲线

引入Stribeck摩擦模型代替图2里固定黏性摩擦常数FL，使得被控对象变为一个时变的非线性系统。

3 滑模变结构控制器的设计

其中，C1、C2、C3为常数，其特征方程为p3＋C3p2＋C2p＋C1＝0，根据劳斯—赫尔维茨判据可知，C1＞0，C2＞0，C3C2＞C1时线性系统稳定。

对滑模面函数求导：

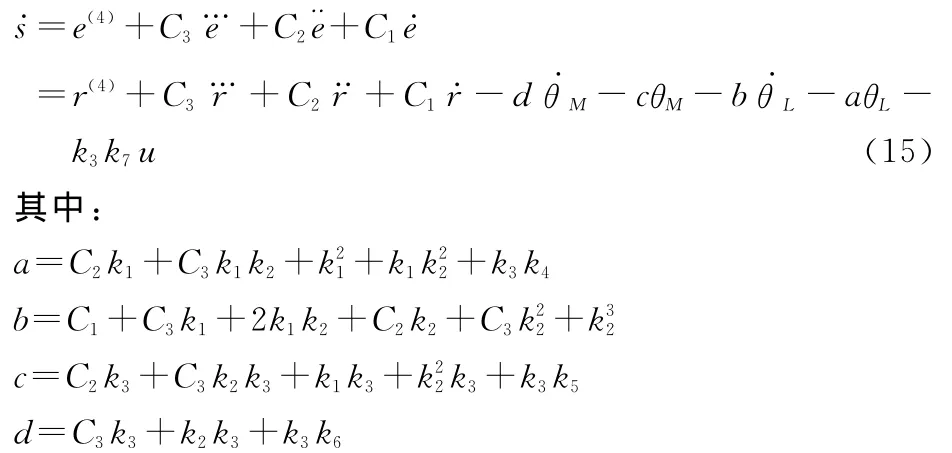
用指数趋近律方法设计控制律u：

不难证明s s·＝－εsgn（s）×s－ks2＜0，满足滑模变结构控制的3个基本条件［4］。于是，可设置滑模变结构控制器为：

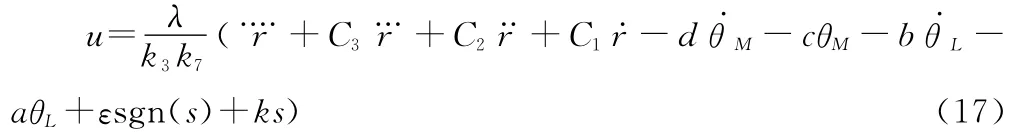
其中，λ是控制器的输出放大倍数，能灵活控制输出大小，使控制量在合理范围之内。

4 仿真结果

取控制参数C1＝2000，C2＝266.7，C3＝10，ε＝100，k＝50，λ＝0.05，对于同样的被控对象采用滑模变结构控制进行阶跃响应实验，其响应曲线如图4所示，对比图3采用经典PID控制的阶跃响应曲线，其控制效果并没有明显的不同，只是在过渡时间和超调量方面稍微优于PID控制。

图4 滑模变结构控制位置阶跃响应曲线

但是稳定转台伺服系统各部分参数会因系统状态及所处环境不同而不尽相同，同样的一套控制参数是否能够适应不同的系统参数，是衡量一个控制器鲁棒性好坏的重要指标。假设电机电枢转动惯量发生了变化，由原先的0.0114kg·m2变为0.0228kg·m2，开展阶跃实验进行对比，如图5所示。

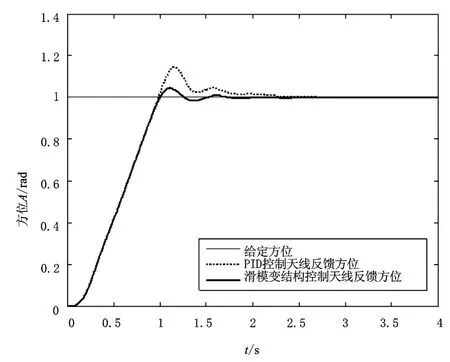
图5 电枢转动惯量变化时跟踪曲线对比

利用Stribeck摩擦模型来代替固定黏性摩擦常数，模拟参数时变系统，完成类似的阶跃实验，如图6所示。

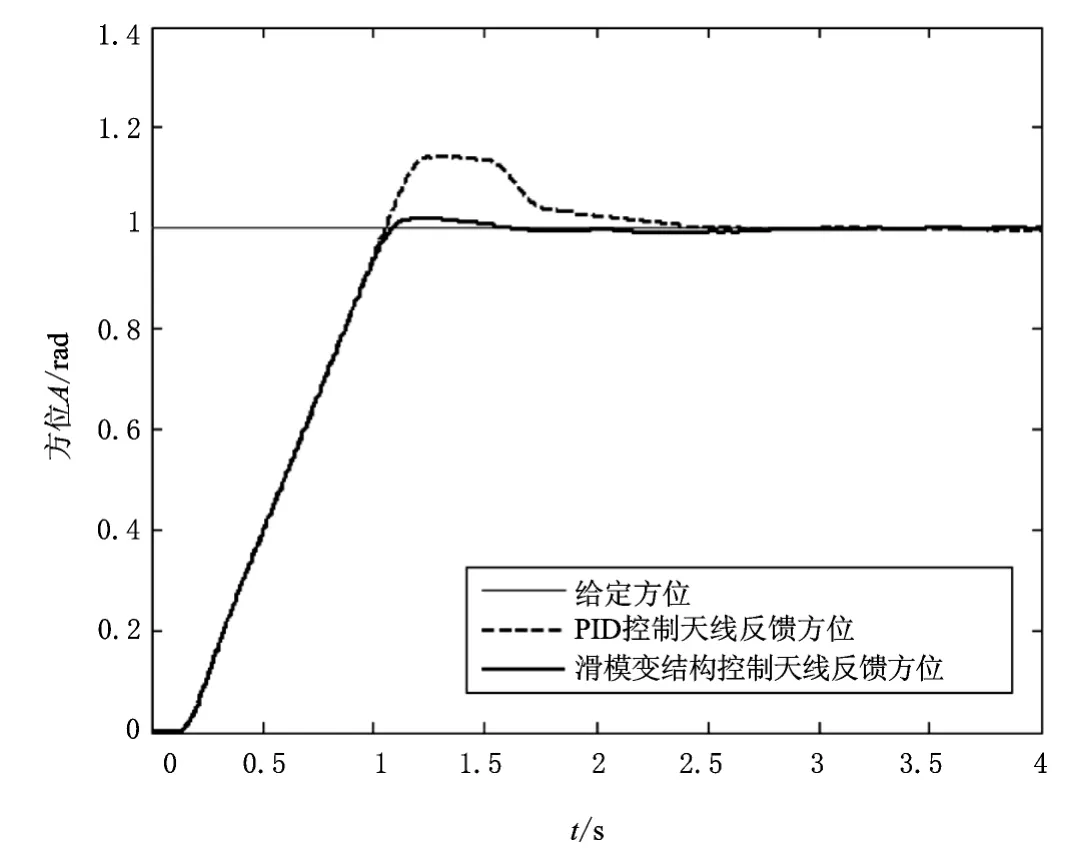
图6 摩擦时变系统跟踪曲线对比

2种控制方法控制参数都保持不变，当在作用在负载上的力矩处增加TO＝－1000N·m的持续外部干扰时，可以得到如图7所示的对比曲线。

从图4～7可以看出：系统参数变化或外部出现干扰时，同样的阶跃响应实验，滑模变结构控制器跟踪曲线形状虽然发生了变化，但是过渡时间、稳态误差等指标并没有多大变化。反观PID控制器，其超调量和稳定时间明显增加，控制效果显著下降。这证明滑模变结构控制鲁棒性更好，具有很强的抗干扰能力。

5 结语

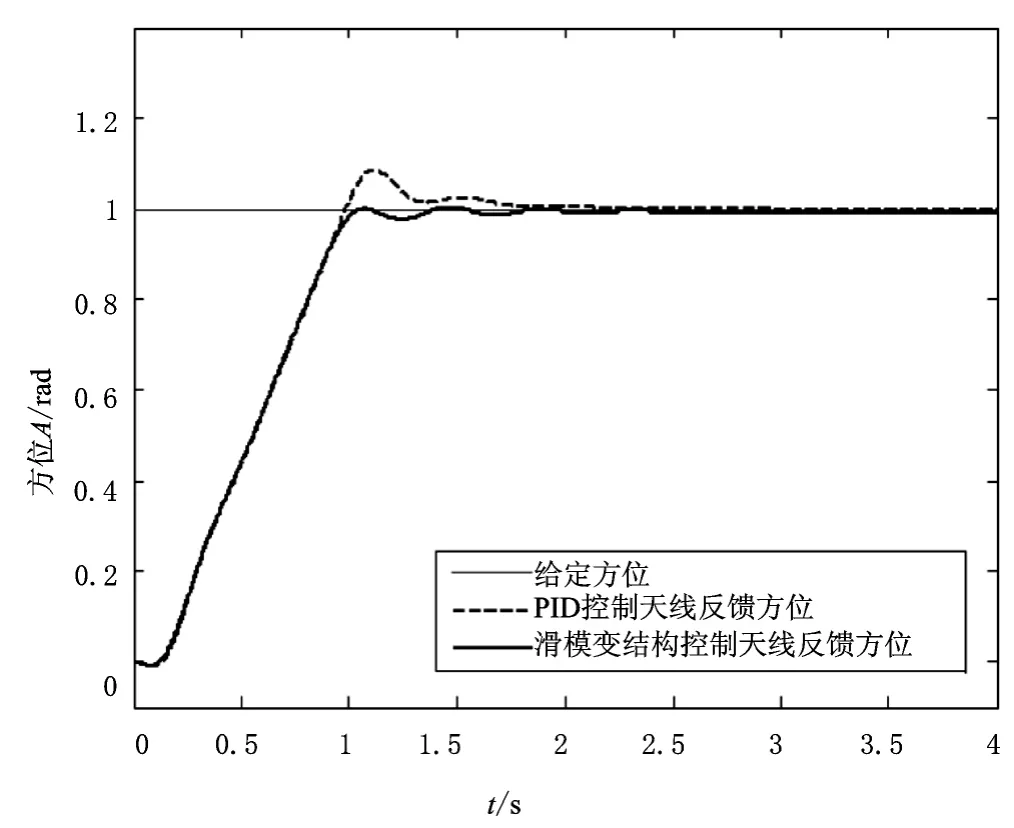
图7 带有外部干扰时跟踪曲线对比

将伺服控制单元和天线负载合在一起看作控制对象，建立了三质量数学模型，推出了被控对象的四阶传递函数。另外，由于摩擦对伺服控制有着重要的影响，本文结合Stribeck摩擦模型对伺服控制方法进行了深入研究。

针对经典PID控制方法存在的局限性，本文根据滑模变结构控制理论，构造了滑模面函数，设计了控制律，从而建立了滑模变结构控制器，通过计算机仿真的方式，与经典PID控制方法进行了对比，证明滑模变结构控制在动态响应、抗参数摄动、抗干扰能力等方面具有较大优势，可以在车载雷达稳定转台伺服控制系统中推广应用。

［1］刘世挺.雷达伺服控制技术的新发展［J］.火控雷达技术，2002，27（1）

［2］邹云飞，刘金琨，王宗学.转台伺服系统滑模变结构控制器的设计与仿真研究［J］.计算机仿真，2002，19（2）

［3］刘金琨.滑模变结构控制MATLAB仿真［M］.北京：清华大学出版社，2012

［4］陈志梅，王贞艳，张井岗.滑模变结构控制理论及应用［M］.北京：电子工业出版社，2012