自抗扰参数模糊自整定无刷直流电机控制研究＊

李孟秋，汪 亮，黄 庆，唐 磊，赵盈盈

（湖南大学 电气与信息工程学院，湖南 长沙 410082）

自抗扰参数模糊自整定无刷直流电机控制研究＊

李孟秋，汪 亮†，黄 庆，唐 磊，赵盈盈

（湖南大学 电气与信息工程学院，湖南 长沙 410082）

在电机控制当中，自抗扰控制器（ADRC）是提高系统鲁棒性的有效手段之一，但是其需整定的参数过多，不便于实际操作，本文结合模糊控制技术，对自抗扰控制器的参数进行自整定，不仅保持了ADRC原有的优良性能，而且提高了其自适应能力.同时结合无刷直流电机本身的特性，推导出了BLDCM作为被控对象的二阶状态方程，仅用一个参数模糊自整定的自抗扰控制器就实现了无刷直流电机的运行控制，保证了BLDCM控制系统结构的简单性.仿真表明，此控制系统对BLDCM的内部参数的摄动和外界扰动具有很强的自适应性和鲁棒性，并且结合实验验证了其可行性和有效性.

无刷直流电机；自整定；模糊控制；自抗扰

永磁无刷直流电机（BLDCM）由于其结构简单、输出转矩大、运行效率高、维护方便等优点，被广泛应用于国防、航空航天、机器人、汽车电子、家用电器等领域中［1－8］.由于永磁无刷直流电机本身是一个非线性、强耦合、多变量的系统，实际使用时其本身的某些参数会围绕额定值有一定的摄动，外部负载的变化也会带来扰动，所以其控制系统的鲁棒性和自适应性一直欠佳，这使得永磁无刷直流电机的应用受到了一定的限制.

许多学者在这方面进行了大量的研究工作.文献［9－10］提出了自抗扰控制技术，该技术被广泛应用于各个领域，在电机控制领域得到了很高的关注及应用.文献［11］将神经网络控制算法与自抗扰控制技术相结合，虽然在增强系统的自适应方面效果不错，但是运算量大，结构复杂，数据量过大时会造成系统响应迟缓，影响系统响应的灵敏性，不便于实际运用.文献［12］提出了应用模糊控制技术来控制无刷直流电机的运行，虽然在提高系统鲁棒性方面效果显著，但是将整个电机作为对象设计模糊控制器，设计过程过于繁琐，工作量太大.文献［13］设计了两个一阶自抗扰控制器实现了对电机运行的控制，抑制了电机运行时的转矩波动，但是单个自抗扰控制器的可调参数已经较多，两个ADRC调整时需整定的参数则过多，给实际运用带来不便.综上所述，对于BLDCM来说，设计一个自适应能力强，整定参数少，抗扰动性能好的控制器具有十分重要的实际运用意义.

1 自抗扰控制器的数学模型

自抗扰控制器（ADRC）主要由跟踪微分器（TD）、扩 张 状 态 观 测 器 （ESO）、非 线 性 组 合（NLSEF）和扰动补偿4个部分组成.如果被控对象是一个n阶的受未知外扰的非线性不确定对象，表达式为：

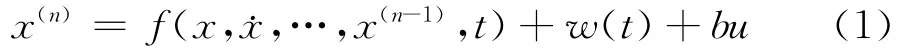
其中f（x，˙x，…，x（n－1），t）是未知函数，w（t）是未知外扰，x是测量输入，u为控制输入，b为控制输入系数.

这里考虑二阶不确定被控对象，表达式为：

2 自抗扰的参数的模糊自整定

传统的自抗扰控制器，在继承了PID控制器结构简单，鲁棒性强优点的同时，克服了其误差取法不合理、没有误差微分提取办法、组合方式不理想等缺点.虽然性能优越，但是在实际应用中，很多参数的调整，需要工作人员根据经验反复试验后才能达到较好的效果，给实际应用带来诸多不便.模糊控制技术是解决这一问题的有效方法之一.模糊控制理论是建立在人工经验基础之上的，运用模糊数学的理论和方法，把规则的条件和操作用模糊集表示，并把这些模糊控制的规则及有关的信息存入知识库中，然后根据控制系统的实际情况进行响应，运用模糊推理，即可实现自抗扰参数β0，β1和β2的自动调整.

自抗扰参数的模糊自整定方法，是受模糊PID控制器的自整定启发，将非线性组合（NLSEF）的输入，即误差e1，e2两个量作为模糊控制部分的输入，运用模糊控制规则，在线实时地计算出所需的参数，以满足不同时刻的自抗扰参数自整定的要求.自抗扰参数的模糊自整定结构框图如图1所示.

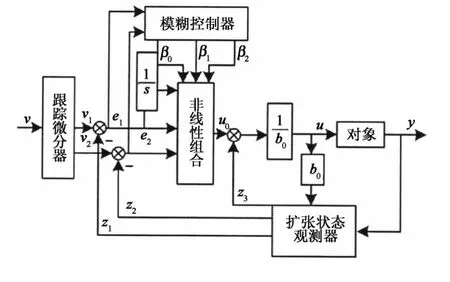
图1 自抗扰参数的模糊自整定结构框图Fig.1 ADRC parameters of fuzzy self-tuning structure diagram

对于被整定的参数β0，β1和β2，其整定过程与PID参数的模糊整定相近，β0相当于积分参数，β1相当于比例系数，β2相当于微分系数，由此针对这3个参数分别制定了参数整定模糊控制表，如表1～表3所示.

根据各模糊子集的隶属度赋值表和各参数模糊控制模型，应用模糊合成推理设计β0，β1和β2参数的模糊矩阵表，查出修正参数代入下式计算：

式中β00，β10和β20为β0，β1和β2的初始值，按照此式计算即可得到整定后的β0，β1和β2.此模糊控制器结合ADRC就构成了ADRC控制器的参数模糊自整定.

表1 可调参数β0模糊控制表Tab.1 Tunableβ0fuzzy control table

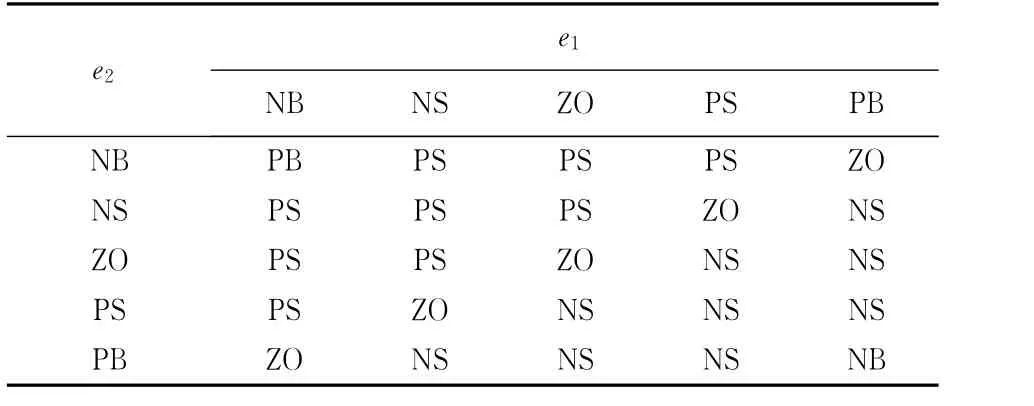
表2 可调参数β1模糊控制表Tab.2 Tunableβ1fuzzy control table

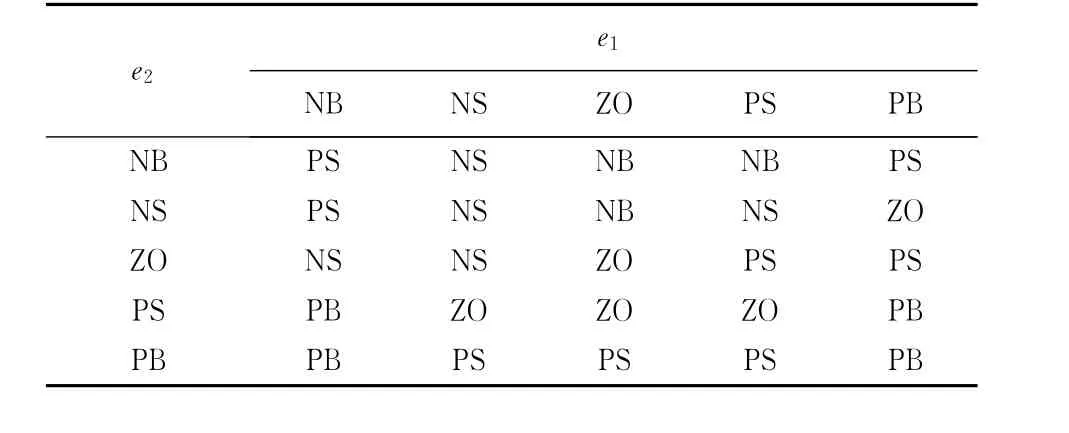
表3 可调参数β2模糊控制表Tab.3 Tunableβ2fuzzy control table

3 BLDCM控制系统方案

根据无刷直流电机的数学模型，在无刷直流电机定子绕组为Y型连接，忽略电机铁心饱和，不计电枢反应和忽略齿槽效应时，对于定子绕组的相电压有如下矩阵表示：

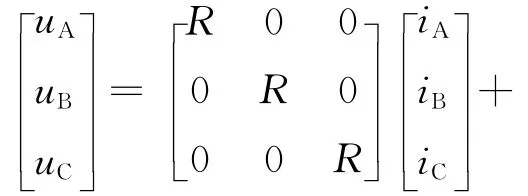
式中uA，uB，uC为相电压；R 为相电阻；iA，iB，iC为相电流；L为相绕组自感；M 为相绕组互感；eA，eB，eC为相反电势.

可近似认为每个时刻，导通的两相绕组电流大小相等，方向相反，对于A，B相绕组有：

若不计换相的暂态过程和不考虑反电动势的梯形斜边，则A，B相稳态导通时，反电动势的大小相等，符号相反，式（12）可以写为：

其中Ud是直流母线电压，r是绕组线电阻，LX是绕组等效线电感，ke是线反电势系数，ω为电机机械角速度，线电压uBC，uAC与此同理.

对于无刷直流电机其电磁转矩的表达式有：

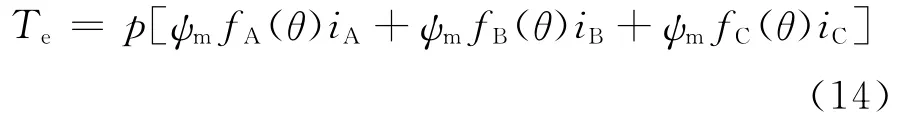
式中f（θ）为相反电动势的波形函数，ψm为每相绕组匝链永磁磁链的最大值，p为电机极对数.

绕组中仅有两相流过电流，大小相等方向相反，同时f（θ）的符号对不同的相绕组来说总是相反的，则式（14）可以简化表达为：

其中TL为负载转矩，J为转子转动惯量，B为黏滞摩擦系数.

根据文献［14］可知，PWM放大器自身的传递函数可以近似为一个比例环节，如式（18）：

式中k为PWM放大倍数，u为触发电路的控制电压.

根据式（5）和式（20）可得电机运行的扩张状态观测器（ESO）方程为：

式中z1为实际转速的状态估计，z2为实际转速的微分估计，w＊（t）为扰动量w（t）的估计值.

非线性组合部分（NLSEF）和最终补偿扰动形成的控制量方程为：

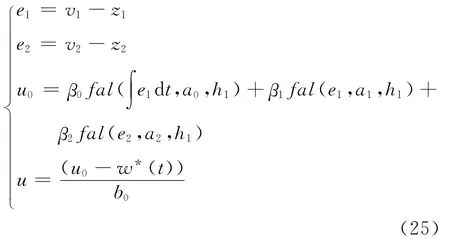
控制器的结构如图2.

根据式（19）和各结构的传递函数，可建立控制系统的结构框图，将触发电路的触发电压u作为被控对象的输入，无刷直流电机实际转速ω作为输出，在控制器的输入端给定速度ω＊，经跟踪微分器（TD）产生跟踪信号，再经模糊控制器实时计算产生合适的参数β0，β1和β2，送入非线性组合部分（NLSEF），扩张状态观测器实时估计扰动量和转速值，反馈形成输出量u.整个系统中，将外加负载TL视为外部扰动量，将无刷直流电机内部的参数摄动视为内部扰动，结合改进的ADRC构成了无刷直流电机的整个运行控制系统.具体结构框图如图3所示.

图2 运行控制器结构框图Fig.2 Running controller block diagram

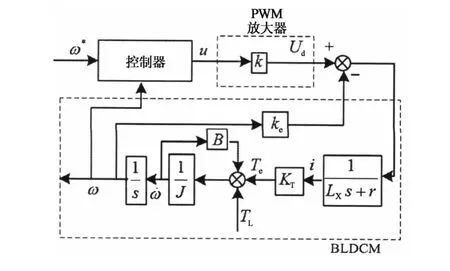
图3 系统控制结构框图Fig.3 System control block diagram

4 仿真分析与实验结果

为了验证运行控制器对无刷直流电机控制的可行性和有效性.以MATLAB中的simulink单元作为仿真实验平台，搭建仿真模型，进行验证.仿真用电机模型参数如下：转动惯量J＝0.01kg·m2，电机转矩系数KT＝0.72N·m／A，线反电势系数ke＝0.132V·min／r，绕组等效线电感LX＝0.01H，绕组线电阻r＝0.7Ω，黏滞摩擦系数B＝0.01N·m·s2／rad，额定电压UN＝200V，额定转矩TN＝16 N·m，额定转速nN＝1 200r／min.

仿真中，对于ADRC中的跟踪微分环节（TD）其参数整定比较简单，跟踪速度因子r越大安排的过渡过程就会越短，反之则越长，这里取r＝1.0×104，取积分步长h＝0.01，TD的参数确定后可保持不变，扩张状态观测器（ESO）的参数，由其内部参数之间的关系可自动生成，非线性组合部分（NLSEF）的参数则由模糊控制器自行整定生成，启动时，先预设参数，然后由模糊控制器进行在线调整，预设参数β0＝180，β1＝1 800，β2＝1 000.

为了验证本文设计的系统对于各种扰动具有更高的自适应性和鲁棒性，仿真中人为设定了内部参数摄动和外部负载扰动，以观测系统的响应，并与传统的不具备参数自整定性的ADRC控制器的系统进行对比.

由于无刷直流电机的电枢反应的非线性，转动惯量的变化以及绕组的电阻值的变化等，内部经常会出现摄动，仿真中，令转动惯量，绕组阻值，反电势系数，电机转矩系数随时间围绕额定值按表4中设定进行阶跃变化，其他参数不变，空载启动直至速度达到额定值.

表4 参数摄动表Tab.4 Parameter perturbation table

仿真得到的转速响应曲线如图4所示.

从图中可以看出，在无刷直流电机的内部参数出现轻微摄动，甚至是较大摄动时，本文所设计的系统的速度响应曲线相比传统的ADRC系统，波动非常小，基本没有速度偏差.证实了在内部参数摄动环境下，本系统具有较强的自适应性和鲁棒性.

考虑外部负载变化引起的扰动响应，仍由空载启动，运行至额定转速，然后根据表5阶跃变化负载转矩，观测转速响应.

图4 内部参数摄动时转速响应曲线Fig.4 Internal parameter perturbations speed response curve

表5 负载扰动表Tab.5 Load disturbance table

仿真得到的转速响应如图5所示.

图5 负载扰动时转速响应曲线Fig.5 Load disturbance speed response curve

从图5中可以看出，由于具有参数自整定性的自抗扰控制器可以根据外部变化自动调整参数，能够更好地对外部扰动进行补偿，在外部负载转矩发生变化时，相比传统ADRC控制系统，本文所设计的系统具有更小的转速波动量，而且能够在更短的时间内重新进入稳定状态.再次证明了本系统具有更好的自适应性和鲁棒性.

将内部参数扰动和外部负载扰动同时进行，得到的转速响应曲线如图6所示.

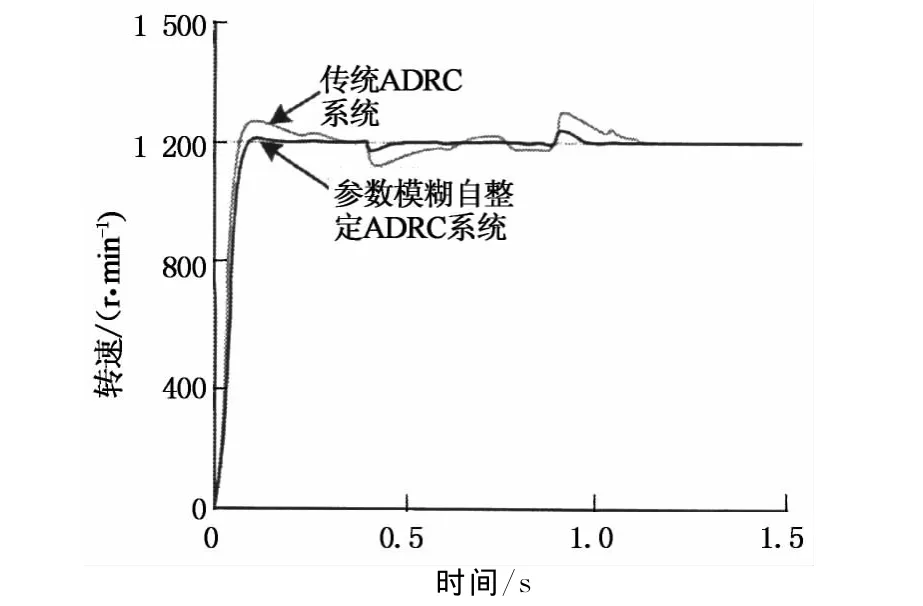
图6 内外扰动同时作用时转速响应曲线Fig.6 Internal and external disturbances simultaneously rotational speed response curve

从图中可以看出，相比纯ADRC系统，本系统的鲁棒性和自适应性明显更优秀.

本系统的实验验证是在基于TI公司生产的TMS320F2808的DSP处理核心的实验平台上完成的.电机参数与仿真中电机参数一致，实验平台的硬件框图和如图7所示，自抗扰控制器和模糊控制器以及各种控制算法由软件编写实现.

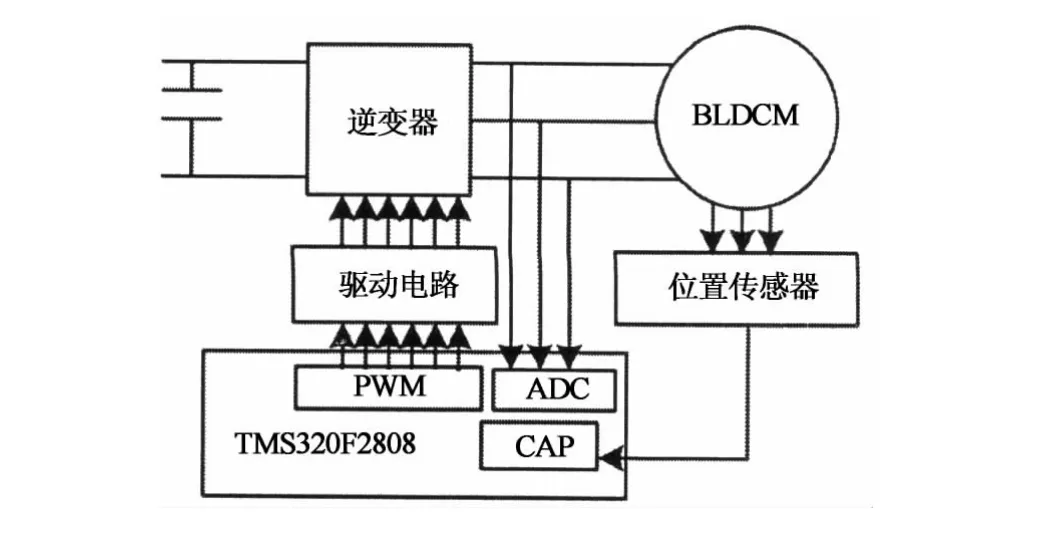
图7 实验平台硬件结构框图Fig.7 Hardware block diagram of the experiment

实验中，BLDCM在安装时使用立式安装，接扭矩功率测量仪，然后与交流变频电回馈加载器相连接，利用加载器控制柜控制加载，如图8所示.

图8 实验平台Fig.8 Experimental platform

由于电机内部参数摄动不便人为给定，因此只给定外部负载变化，但是在电机运行中，参数摄动仍然存在，只是不受人为控制.电机由空载启动，在1s时由加载器加负载转矩TL＝5N·m，由软件内置功能可观察到电机转速响应曲线如图9所示，图10和图11为图9中放大观测部分波形.

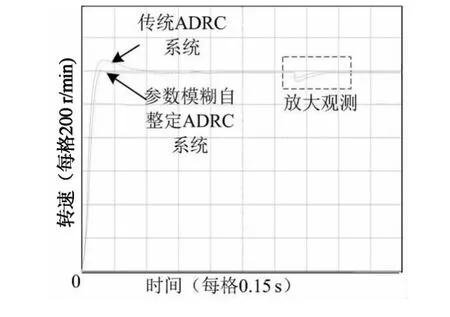
图9 扰动时转速响应曲线Fig.9 Disturbance speed response curve

图10 放大观测的传统ADRC系统转速变化Fig.10 Enlarge observing traditional ADRC system speed changes

图11 放大观测的参数模糊自整定ADRC系统转速变化Fig.11 Enlarge observed ADRC parameters of fuzzy self-tuning system speed changes

从图中可以看出，对于突加负载，本系统比传统ADRC的控制系统表现出更小的波动，速度稳定也更加迅速.证明本系统具有更好的自适应性和鲁棒性.

加载前后电机电流变化对比如图12.

图12 加载前后电机电流变化对比Fig.12 Motor load before and after current changes comparison

从图中可以看出传统ADRC系统加负载后电流增大，但达到稳定状态的时间相对缓慢，具有参数模糊自整定ADRC的系统在受到外部负载扰动后能够迅速做出反应，增大电流，在相对较短的时间内达到稳定状态，自适应能力更强，稳定性更好.

仿真和实验波形基本吻合，共同说明了本系统的具有可行性，鲁棒性好，自适应性强.

5 总 结

本文将模糊控制技术和自抗扰技术应用于永磁无刷直流电机的调速控制当中，首先应用模糊控制技术解决了自抗扰控制器的可调参数多，操作不便，然后根据无刷直流电机本身的特性推导出了适合其本身的二阶带参数自整定性的自抗扰控制器，解决了参数调整困难，控制器繁杂，不利于广泛应用的问题.根据理论设计，利用仿真和实验，验证了在各种扰动下的系统性能，证明本文所设计的控制系统自适应能力强，鲁棒性好，可行性高.

［1］ JOICE C S，PARANJOTHI S R，KUMAR V J S.Digital control strategy for four quadrant operation of three phase BLDC motor with load variations［J］.Industrial Informatics，IEEE Transactions on，2013，2（9）：974－982.

［2］ 夏长亮，张茂华，王迎发，等.永磁无刷直流电机直接转矩控制［J］.中国电机工程学报，2008，28（6）：104－109.

XIA Chang-liang，ZHANG Mao-hua，WANG Ying-fa，et al.The direct torque control for permanent magnet brushless dc motors［J］.Proceedings of the CSEE，2008，28（6）：104－109.（In Chinese）

［3］ 黄庆，黄守道，匡江传，等.基于模糊自抗扰的PMSM无速度传感器控制［J］.湖南大学学报：自然科学版，2012，39（7）：37－44.

HUANG Qing，HUANG Shou-dao，KUANG Jiang-chuan，et al.PMSM sensorless control based on fuzzy active-disturbance rejection［J］.Journal of Hunan University：Natural Sciences，2012，39（7）：37－44.（In Chinese）

［4］ WEN Chien.Simplifying BLDC motor control：A tailored solution delivers precision and efficiency［J］.Electronic Component News，2013，57（5）：20－45.

［5］ BOUGHABA Abdelali，CHAABANE Mabrouk，BENAGGOUNE Said.Robust sensorless control of BLDC motor using second derivative function of the sum of terminal voltages［J］.Serbian Journal of Electrical Engineering，2013，10（2）：275－291.

［6］ KIM Hong-seok，YOU Yong-min，KWON Byung-il.Rotor shape optimization of interior permanent magnet BLDC motor according to magnetization direction［J］.IEEE Transactions on Magnetics，2013，5（49）：2193－2196.

［7］ LYDIA Anu-jose，KARTHIKEYAN K B.A comparative study of sinusoidal PWM and space vector PWM of a vector controlled BLDC motor［J］.International Journal of Advanced Research in Electrical，Electronics and Instrumentation Engineering，2013，6（2）：2662－2668.

［8］ 高瑾，胡育文，黄文新，等.超空间矢量下的无刷直流电机直接转矩控制［J］.中国电机工程学报，2007，27（24）：97－101.

GAO Jin，HU Yu-wen，HUANG Wen-xin，et al.The direct torque control of brushless dc motor based on the hyper space vector［J］.Proceedings of the CSEE，2007，27（24）：97－101.（In Chinese）

［9］ 韩京清.从PID技术到“自抗扰控制”技术［J］.控制工程，2002，9（3）：13－18.

HAN Jing－qing.From PID technique to active disturbances rejection control technique［J］.Control Engineering of China，2002，9（3）：13－18.（In Chinese）

［10］韩京清.自抗扰控制技术［J］.前沿科学，2007，1（1）：24－31.

HAN Jing－qing.Auto disturbances rejection control technique［J］.Frontier Sicence，2007，1（1）：24－31.（In Chinese）

［11］吴其洲.DRNN-ADRC异步电机直接转矩控制系统研究［J］.控制工程，2011，18（3）：335－337.

WU Qi-zhou.Study on direct torque control of induction motor based on DRNN-ADRC［J］.Control Engineering of China，2011，18（3）：335－337.（In Chinese）

［12］李实求，郝帅，马旭，等.无刷直流电机双闭环模糊自适应控制方法研究［J］.电气传动，2012，42（7）：61－63.

LI Shi-qiu，HAO Shuai，MA Xu，et al.Study of double closed loops fuzzy adaptive control method of brushless direct current motor［J］.Electric Drive，2012，42（7）：61－63.（In Chinese）

［13］夏长亮，李正军.基于自抗扰控制器的无刷直流电机控制系统［J］.中国电机工程学报，2005，25（2）：82－86.

XIA Chang-liang，LI Zheng－jun.Control system of brushle ss dc motor based on active-disturbance rejection controller［J］.Proceedings of the CSEE，2005，25（2）：82－86.（In Chinese）

［14］李华德.电力拖动控制系统［M］.北京：电子工业出版社，2006：100－109.

LI Hua-de.Electric drive control system［M］.Beijing：Electronic Industry Press，2006：100－109.（In Chinese）

Brushless DC Motor Control Based on Fuzzy Self-tuning of Active-disturbance Rejection Parameters

LI Meng－qiu，WANG Liang†，HUANG Qing，TANG Lei，ZHAO Ying－ying

（College of Electrical and Information Engineering，Hunan Univ，Changsha，Hunan 410082，China）

In the permanent magnet brushless DC motor（BLDCM）control system，a new ADRC brushless DC motor control system was propsed in order to enhance the robustness and adaptability of the control system and to simplify the controller structure and the debugging process.In motor control，auto disturbance rejection controller（ADRC）is the effective means to improve the robustness of a system，but it has a lot of parameters to be adjusted，which is not good for practical application.This paper used fuzzy control technology to facilitate ADRC parameter self-tuning.This method not only maintains the original excellent performance of ADRC，but also improves the adaptive capacity.Combined with the characteristics of brushless DC motor itself，this paper deduced the second-order equation of BLDCM by using only one parameter fuzzy self-tuning ADRC to achieve a brushless DC motor operation control system.Simulation results have shown that this control system has strong adaptability and robustness in the condition of BLDCM internal parameter perturbation and external disturbances.Experiment results have also shown the feasibility and effectiveness of this system.

book=72,ebook=8

brushless DC motor；self-tuning；fuzzy control；auto disturbance rejection controller

TM301.2

A

1674-2974（2014）05-0071-08

2013-11-25

国家国际科技合作项目（2011DFA62240）；国家“十二五”科技支撑计划重点项目（2012BAH11F03）

李孟秋（1968－），男，湖南益阳人，湖南大学副教授

†通讯联系人，E-mail：xtuwang＠163.com