二维流形图形建模系统完备操作集研究＊

费耀平，陈建二，陈松乔，李 敏

（中南大学 信息科学与工程学院，湖南 长沙 410083）

二维流形图形建模系统完备操作集研究＊

费耀平，陈建二，陈松乔，李 敏†

（中南大学 信息科学与工程学院，湖南 长沙 410083）

针对目前大多数二维流形建模系统不能保证二维流形结构的问题，如欧拉操作会产生非二维流形网格结构，通过对基于网格结构的二维流形建模系统中的各种数据结构及非流形和流形结构的研究，提出了一套新的基于图形旋转系统的完备的网格建模操作.与现有二维流形建模系统中的数据结构和网格建模操作相比，新提出的数据结构和网格建模操作更加直观有效并更方便用户使用.

欧拉操作；图形建模；二维流形；网格结构

网格是计算机图形学中最常用的结构［1－2］.具有简单有效的用户接口的二维流形建模系统是计算机图形学与计算机辅助设计中的重要问题.现有的二维流形建模在处理非流形结构时，通常会使建模算法变得非常复杂［1，3］.另外，一些广泛使用的建模操作如细分算法需要更有效的二维流形结构，否则细分操作执行在非二维流形结构上时，这些建模系统如Maya可能无法正常工作.

理论上说，一个二维流形的网格结构由3个主要部分组成：顶点集、边集、和面集以及这些部分间的9种邻接关系［4］.描述网格结构已有许多数据结构，一些数据结构是基于面集的［5－6］，另一些是基于边集的.最有名的基于边集的表示是Baumgart提出的翼型边结构（winged-edges structure）［7］及其以后的许多翼型边结构的变种［8－9］.这些数据结构可以用来描述网格在二维流形上的嵌入，也可以用来描述网格在非二维流形上的嵌入.

另一个重要问题是应用在网格结构上的操作集.如果操作集中每一个操作作用于一个二维流形上都产生一个有效的二维流形并且每个二维流形都能由操作集中的操作产生，则我们称这一操作集是一个完备操作集.例如，在实体建模中，应用最多的是集合操作，但集合操作可能产生非二维流形结构［1］.因此，集合操作不是一个完备操作集.

Mantyla［2］研究了欧拉操作并证明它们对二维流形建模形成一个完备操作集.Guibas and Stolfi［10］在四方边结构的基础上提出了接合（splice）操作.并证明这一操作也形成一个完备操作集.另外还有其他对这个方向的研究［1－2］.

一些学者提出了用于评价二维流形网格建模方案的质量准则［1－2］，包括：有效性（结构能否有效表示所有二维流形结构），完备性（网格建模操作集是否是一个完备操作集），简单性（结构与操作是否简单直观）和效率性（结构与操作是否有高效率的数据结构和算法）.

本文将进一步研究网格结构建模方面的上述标准，并提出一套新的网格结构建模操作集，证明其形成一套二维流形网格建模的完备操作集.与现有二维流形建模系统相比，新提出的数据结构和网格建模操作更加直观有效并更方便用户使用.

1 二维流形的翼形边结构和DLFL结构

一个二维流形是一个拓扑空间，其中每个点都有一个邻域与开单位圆同胚.一个二维流形如果不包含一个墨比策带，则这一二维流形称为定向的.本文假定讨论中所有的二维流形都是定向的.一个连通的二维流形称为一个曲面.因此，一个二维流形是多个不相交的曲面的并集.根据欧拉特征定理［11］，每个曲面同胚于有0个或多个柄的球面S.球面S拥有的柄数称为曲面的亏格.一个二维流形的亏格是其曲面亏格的和.

一个二维流形S上的网格G指相应二维流形S上图G的嵌入，即从图G到二维流形S的一个一对一的连续映射ρ.图G不一定要连通，也允许同一顶点对之间有多条边以及一个顶点为同一边的两个端点.如果每个S-ρ（G）的局部最大连通子空间都同胚于开单位圆，则称此网格G为一正常嵌入网格.本文只考虑正常嵌入网格.每个S-ρ（G）局部最大连通子空间加上图G中包围此子空间的边称为网格的一个面.对于一个亏格为g的二维流形上的网格G，假定曲面数目、顶点数目、边的数目、与面的数目分别为d，v，e，f，则著名的欧拉－庞加莱定理可由这些参数表示如下：

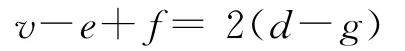
令G为二维流形S上的一个网格.G中的每个顶点v在S上有一个同胚于开单位圆的邻域N.相交于顶点v的边在N中有一个循环排列顺序（按逆时针顺序排列）.这一顺序对表示一个二维流形网格非常重要.Baumgart提出的经典翼型边结构［7，12］本质上来说是基于此形式上.翼型边结构的主要单元是边结点.每个边结点由9个单元组成：（name，vs，ve，fcw，fccw，ncw，pcw，nccw，pccw），name是边的名字；vs与ve是边的起始与结束端点（也就为边指定了一个方向）；fcw与fccw表示当沿着边的方向行走时边的左边和右边的面的名字；ncw与pccw分别为面fcw和面fccw中的下条边，而pcw与nccw分别为当逆着边的方向行走时面fcw和面fccw中的下条边.如图1所示.

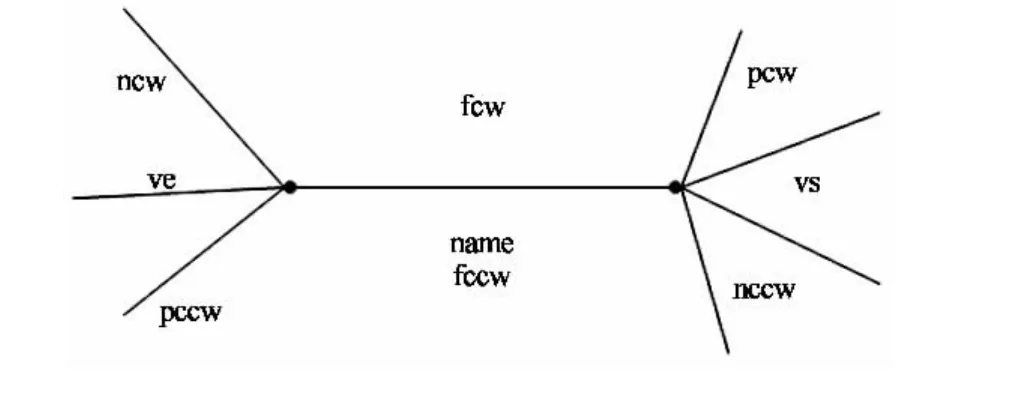
图1 翼型边结构中一个边结点的9个单元Fig.1 A edge node in the winged-edge structure

Guibus与Stolfi［10］研究四方边结构时定义了网格中边的代数式与其对偶式.每条边给定一个确定方向，从而确定了边的左面和右面.由此，每条边有4个不同的方向，并且有4种属性：两个端点Org与Dest（等价于翼型边结构中的vs与ve），二维流形上边的两侧上的左边面与右边面（等价于翼型边结构中的fcw与fccw）.在定向的有向边集合上通过定义Flip，Onext与Rot3个函数引入了边代数.Flip定义了边翻转的方向，Onext给定了在Org函数基础上的下一条边，是按照其朝以逆时针的顺序来看（与翼型边结构中的nccw类似），Rot是旋转边（这一定义较复杂在此略去其细节描述）.定向与不定向的二维流形均可由边代数描述.边代数必须对原网格及其对偶网格给出结构.Guibus与Stolfi提出了用四方边结构来表示网格结构的边代数［10］.

在基于面的数据结构中，Akleman和Chen［5］介绍一种数据结构DLFL（Doubly Linked Face List）.对于图形旋转系统的基本操作，采用DLFL数据结构有着很好的空间和时间复杂度.DLFL数据结构是基于面表达的数据结构，是一个三元组结构L＝＜F，V，E＞，｛F｝是包含所有的面的集合，每个面可以用树结构来表示，叶节点为围成面的面角序列.｛V｝是包含所有定点的集合，其中每一项元素是一个指向面中叶节点的指针.｛E｝是包含所有边的集合，其中每一项元素指向共享该边的两个或多个面对应的两个面角，DLFL的表达实例如图2所示［13］.

图2 正四面体的DLDF数据结构表示Fig.2 DLDF data structure for a regular tetrahedron

2 扩展的图形旋转系统和操作的完整性和稳固性实现

2.1 扩展的图形旋转系统

假定G是嵌入二维流形S上的一个网格.图G中每个连通子图对应S中一个特定曲面［14］.S上每个点有一个同胚于开单位圆的邻域，假设站在S上对应于图的顶点v的位置上，则我们可以看见在v点的小范围邻域中，相交于v点的所有边端点按逆时针的方向形成一个旋转顺序排列.这给出了这些边端点的一个旋转顺序［14］.例如，如果v是没有相交边的孤立顶点，则包含v的曲面是亏格为0的球面S2，而S2－ ｛v｝同胚于一个边界退化为单个点v的开单位圆［15－16］.

因此，网格G在二维流形S上的嵌入对每个G中的顶点的所有边端点都引入了一个旋转顺序.有以下重要概念［17］.

定义1 设G为有n个顶点的图.图G中的每条边有两个不同的边端点.如果对图G中相交于每一顶点的所有边端点给一固定的旋转顺序，则这些对应于顶点的所有边端点的旋转顺序的集合称为图G的一个旋转系统.

备注1 上述的定义是拓扑图论中同一概念的扩展.最初用于拓扑图论的图旋转系统不包括孤立点的概念［13］.这种包含孤立点的扩展的图旋转系统在二维流形网格建模研究中具有重要作用.

备注2 定义的图旋转系统中，图G并不一定要连通，并允许多边（即允许多于一条边与同一顶点对相连）与自循环（即一条边的两个端点可为同一个顶点）.当然，在多边存在的情况下，必须区别有同样端点的不同边.自循环的两个端点也应该被区分.

备注3 图G中一条边的两个对应边端点可用与该边相交的两个顶点来表示.如u和v是不同的顶点，则我们可以用 ＜u，v＞ 和 ＜v，u＞ 来分别表示边 ［u，v］相交于节点u和相交于节点v的两个边端点.如果边 ［u，v］是自循环的，即u＝v，则根据备注2，边［u，u］的两个边端点可区别记为u’和u’’，而其两个边端点为 ＜u’，u’’＞ 和＜u’’，u’＞.如用符号e表示一边端点.则同一条边的另一边端点记为rev（e）.所以，如e＝ ＜u，v＞，则rev（e）＝ ＜v，u＞.

备注4 一个扩展的图旋转系统ρ（G）给出了图G的顶点集和边集.另外，通过由一个叫做Face－Trace的算法［17］，我们可以唯一构造出从一个边端点出发对应的面元素.因此，反复利用FaceTrace算法，可以构造出所有的面元素，从而重构出图G在一个二维流形上的嵌入［17］.事实上，这种二维流形的重构是唯一的，如定理1所述.

定理1［17］一个扩展的图的旋转系统ρ（G）唯一确定了图G在一有效二维流形上的嵌入，从而唯一确定了对应的二维流形.

网格建模中的操作是重要的，特别是对于拥有可靠与强大的用户接口的建模系统.定理1为二维流形的网格建模操作问题提供了坚实的理论基础.二维流形建模在建模操作上存在三个重要的问题，分别为完整性，稳固性与有效性.产生任何二维流形结构需要的操作都是从集合S中得到，那么称集合S是操作上完备的.如果运用集合S中的操作于二维流形都能产生有效的二维流形结构，那么集合S的操作是稳固的.定理1将网格建模操作的健全与完备问题变成基于图形旋转系统的表示问题：只要能证明提出来的操作集合能创建所有且仅限于有效的图形旋转系统，那么就能保证操作集合的健全与完备.

2.2 完备与健全的操作集合

与以往提出的相比，本文提出的建模操作集合更简单，直观与方便用户使用.下面将讨论操作集合的健全性及完备性，操作集合S是“完备”和“健全”的.“完备”的含义是指：通过S中的操作可以构造任意的二维流形体.“健全”的是指：S中的操作对二维流形体是封闭的.考量其在各种建模数据结构上执行的有效性，并与现有的建模操作的各个方面作比较.

第一个操作是边插入操作，简单记作E-INSERT，设ρ（G）为一个图形旋转系统，u和v是G中的两个顶点.在面拐角（＜u，x＞，＜u，x’＞）与（＜v，y＞，＜v，y’＞）间插入一条边［u，v］，也就是在边端＜u，x＞与＜u，x’＞间的旋转点v处插入边端＜u，v＞和在边端＜v，y＞与＜v，y’＞间的旋转点v处插入边端＜v，u＞.与插入相反的为边删除操作，简单记作E-DELETE.同样设ρ（G）为一个图形旋转系统，e＝［u，v］为G中的一条边，删除边e即在旋转点u处删除＜u，x＞和在v处删除＜v，u＞.

其他主要的操作有创建顶点，简单记作V-CREATE，此操作在旋转系统中创建不带边的孤立点，对应相反的操作为移除点，V-REMOVE，是在旋转系统中移除一个孤立点.

定 理 2 由 E-INSERT／E-DELETE 和V-CREATE／V-REMOVE组成的操作集合是完备与健全的.

证 操作集合明显有健全性：在能够表示有效二维流形结构的图形旋转系统上应用4种操作会产生有效的二维流形结构.

前面已经说明，任意二维流形S的多孔网格结构导出唯一的旋转系统ρ（G）.先后运用一系列的EDELETE与V-REMOVE操作后，会得到没有顶点与边的空旋转系统.反过来，即先后运用一系列的V-CREATE与E-INSERT操作后，会从一个空旋转系统中重建旋转系统ρ（G）.由此可见，通过一系列的集合中的操作能得到任何多孔网格结构，任意亏格的曲面也能通过本文提出的操作集合构造出来.证毕

与［2，8］中提出与研究的欧拉操作相比，本文提出的操作集合更加简单、直观、一致和更易于用户使用且提出的集合仅由更少的操作组成.避免了系统层与用户层及内部表示与拓扑完整性的不一致问题.

2.3 基于顶点的数据结构的实现

在邻接表结构上实现 E-INSERT，E-DELETE和 V-CREATE，V-REMOVE操作非常简单.若在面拐角（＜u，x＞，＜u，x’＞）与（＜w，y＞，＜w，y’＞）间插入一条边［u，w］（在表示u的链表中x’在x之后，表示w的链表中y’在y之后），只需在表示顶点u链表中分别包含x与x’的两个结点之间插入包含w的结点和在表示顶点w链表中分别包含y’与y’的两个结点之间插入包含u的结点.同理，在表示顶点u链表中删除w和表示顶点w链表中删除u来在邻接表结构上对边［u，w］实行E-DELETE操作.最后，V-CREATE操作对应的是增加一个带有空链表的新顶点到邻接表中，VREMOVE操作则对应从邻接表中移除一个带有空链表的顶点.

在邻接表上执行 V-CREATE与 V-REMOVE操作所需时间为一常数.而 E-INSERT 与E-DELETE操作执行时则需要查找对应两个顶点的链表，当顶点的价很大时会很耗时.用平衡树代替链表存储与顶点相关的端点，E-INSERT与 E-DELETE操作执行的时间复杂度可以得到改进，只需树大小的对数的时间复杂度［10］.此外，实现中，只需要增加一个边表来支持对结构中边端的有效查找.

2.4 基于边的数据结构的实现

为了实现V-CREATE与V-REMOVE操作，需要在翼型边线结构中引入辅助的顶点表.顶点表中包含顶点结点，其指针指向任意边结点中端点v.孤立顶点包含空指针.实现V-CREATE操作只需简单地往结构中增加一个带空指针的新顶点结点.VREMOVE操作则是从结构中移除一个带空指针的顶点结点.

在翼型边线结构上执行E-INSERT与E-DELETE操作算法见图3，其中子程序FaceTrace即是文献［17］中的FaceTrace的算法.从一个边端点出发，子程序FaceTrace构造出对应的面元素.操作E-INSERT是在面拐角c1＝（＜u，x＞，＜u，x’＞）与c2＝ （＜w，y＞，＜w，y’＞）间插入一条边＜u，w＞，操作E-DELETE则是删除边e.执行操作后，相关边的ncw，pcw，，nccw，pccw部分会更新.需要解释的是对fcw与fccw的更新.首先考虑E-INSERT，如果面拐角c1与c2属于不同的面，那么在它们之间插入边e＝［u，v］的操作得到的一个新面会代替网格中的两个面，这个新面的边界包含e的边端＜u，w＞与＜w，u＞.这种情形下，步骤5中子程序FaceTrace（＜u，w＞）会跟踪新面的边界并适时更新有关边结点中面部分的信息.特别地，步骤6中子程序FaceTrace不会执行.另一方面，如果面拐角c1与c2属于同一面，那么在它们之间插入边e＝［u，v］的操作得到的两个新面会代替网格中的一个面，这两个新面的边界包含e的边端＜u，w＞与＜w，u＞.这种情形下，步骤5中子程序Face－Trace会跟踪一个新面的边界并适时更新有关边结点中面部分的信息.步骤6中子程序FaceTrace则会跟踪另一个新面的边界并适时更新有关边结点中面部分的信息.

图3 翼边结构的E-INSERT和E-DELETE算法Fig.3 E-INSERT and E-DELETE on winged-edge structure

对边e实现E-DELETE操作，如果e的两个端点在两个不同面的边界上，那么删除e会合并两个面为一个面.步骤5中子程序FaceTrace会跟踪新面的边界并适时更新有关边结点中面部分的信息.另一方面，如果e的两个端点在同一面的边界上，那么删除e会分离这个面为两个面.步骤5与步骤6中的子程序FaceTrace会分别跟踪两个新面的边界并适时更新有关边结点中面部分的信息.

算法E-INSERT与E-DELETE的时间复杂度分析.由于每个算法都需执行一个或两个时间复杂度正比于相关面大小的FaceTrace子程序，当面较小时（如在三角化网格上）耗时较小，在面很大的情况下，将耗费大量时间.可以得到定理3的结论.

定理3 对于一般的翼型边线结构，算法E-INSERT与E-DELETE的运行时间复杂度为O（s），s是有关面的大小，特别地，对于没有fcw与fccw信息部分的翼型边线结构其算法E-INSERT与EDELETE的运行时间复杂度为O（1）.

在翼型边线结构上执行E-INSERT与E-DELETE操作可容易地扩展到其他的基于边的数据结构上.

2.5 基于面的数据结构的实现

DLFL结构有一个面表，一个边表和一个顶点表.面表中每个面结点是对应面边界的边端序列，边表中每个边结点有两个指向面表中对应的边端的指针，而顶点表中的每个顶点结点则有一个指向面表中以该顶点为极的边端的指针.

V-CREATE与V-REMOVE操作实现是简单的.V-CREATE（v）创建面表中面边界退化为单个顶点v的面结点，也创建顶点表中的顶点结点，这个结点的指针指向相应的新面.V-REMOVE操作则从面表中移除一个面边界退化为单个顶点v的面结点，也移除顶点表中的表示v的顶点结点.

在DLFL结构上实现E-INSERT和E-DELETE的算法，如图4所示，其正确性可从前面的证明得到检验.下面考虑算法的时间复杂度.

既然边表中的边结点有两个指向面表中的边端的指针，对于每条边，可以在时间为常数的情形下，从面表中获取它的端点.对于面表中的每个面结点f，有一个包含端点的循环链表与面边界对应.如果采用平衡树结构实现这个循环链表（如2－3树结构［1］）那么检测两个端点是否属于同一个面，把一个端点表分为两个，合并两个端点表的操作均可以在时间复杂度为O（s）下完成，s是有关面的大小（更多的细节描述与检验见［17］）.注意到，每次在DLFL结构上执行E-INSERT与E-DELETE算法都是由一个或多个检测测端点表，分离与合并操作组成.因此，在实现面结点端点表的循环链表下，算法E-INSERT与E-DELETE的运行时间复杂度限制为O（log s）.结论如定理4所示.

定理 4 在 DLFL 结构上，V-CEATE 与V-REMOVE操作运行时间复杂度限定为O（1），EINSERT与E-DELETE操作的运行时间复杂度限制为O（log s），s是有关面的大小（至多涉及两个面）.

同时指出在DLFL结构上实现V-CEATE，VREMOVE，E-INSERT与E-DELETE操作，它们的运行时间复杂度与有关顶点的价无关.

图4 DLFL的E-INSERT和 E-DELETE算法Fig.4 E-INSERT and E-DELETE on DLFL structure

3 实验结果

为了验证本文的算法，对于基本的图形旋转系统的操作，插入、删除边，创建，删除点操作都是流形的封闭操作，因此构建的网格结构都是二维流形的.如图5（a）所示，左边分别为构建的一个方体结构、正四面体结构和带柄方体结构，右边为对应的进行一次细分算法的结果.从细分的结果可以看出所构建的基本网格结构是流形的.

4 结 论

带有一个简单而强大的用户接口的健壮的网格拓扑建模是计算机图形学与计算机辅助几何设计中的重点.本文研究了包括对二维流形网格建模的表示，数据结构与操作的一些基本问题.拓展了图形旋转系统在拓扑图论的理论研究并表明扩展了的图形旋转系统为二维流形网格建模提供了一个坚实的理论基础.在此基础上，提出了一种新的二维流形网格建模操作集合，并且证明这个操作集合是完备与健全的，通过这个集合中的操作序列能构造任意的二维流形网格结构.此外，本文还介绍了在基于点，边和面的数据结构上能有效地实现本文的操作.

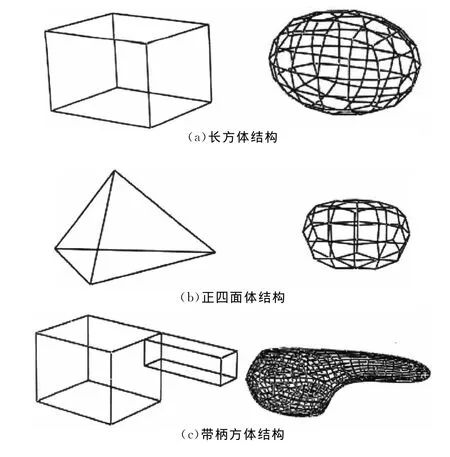
图5 长方体、正四面体和带柄方体结构及其对应的一次细分算法结果Fig.5 Cuboid，regular tetrahedron and cube with handle and their corresponding subdivision results

［1］ HOFFMANN C M，VANECEK G.Fundamental techniques for geometric and solid modeling［J］.Manufacturing and Automation Systems：Techniques and Technologies，1990，48：347－356.

［2］ MANTYLA M.An introduction to solid modeling［M］.Michigan：University of Michigan，Computer Science Press，2007：30－120.

［3］ MANTYLA M.Boolean operations of 2-manifolds through vertex neighborhood classification［J］.ACM Transaction on Graphics，1986，5（1）：1－29.

［4］ WEILER K.Edge-based data structures for solid modeling in curved-surface environments［J］.IEEE：Computer Graphics＆ Applications，1985，5（1）：21－40.

［5］ AKLEMAN E，CHEN Jianer.Guaranteeing the 2-manifold property for meshes with doubly linked face list［J］.International Journal of Shape Modeling，1999，2（5）：149－177.

［6］ 赵明喜，马利庄，毛志宏.基于改进的图形旋转系统的高亏格造型系统［J］.计算机辅助设计与图形学学报，2006，18（3）：421－425.

ZHAO Ming-xi，MA Li-zhuang，MAO Zhi-hong.A high genus modeling system based on improved graph rotation system［J］.Journal of Computer Aided Design ＆ Computer Graphics，2006，18（3）：421－425.（In Chinese）

［7］ BAUMGART Bruce G.Winged-edge polyhedron representation［R］.Stanford：Stanford University，1972.

［8］ BRAID I，HILLYARD R，STROUD I.Stepwise construction of polyhedra in geometric modeling［M］.New York／London：Academic Press，1980：123－141.

［9］ FUJIO Yamaguchi，TOSHIYA Tokiead.Frontiers in computer graphics［M］.Tokyo：Springer Japan，1985：44－65.

［10］GUIBAS L，STOLFI J.Primitives for the manipulation of general subdivision and computation of Voronoi diagrams［J］.ACM Transaction on Graphics，1985，4（2）：74－123.

［11］GROSS J，TUCKER T.Topological graph theory［M］.Mineola，New York：Dover Publications，2001：20－60.

［12］MURALI T，FUNKHOUSER T.Consistent solid and boundary representations from arbitrary polygonal data computer graphics［C］／／Proceedings of the 1997Symposium on Interactive 3DGraphics.ACM，1997：155－162.

［13］张晔芝，谷士文，费耀平.基于图形旋转系统的渐进网格研究［J］.湖南大学学报：自然科学版，2004，31（4）：10－16.

ZHANG Ye-zhi，GU Shi-wen，FEI Yao-ping.Study of progressive mesh based on graph rotation system［J］.Journal of Hunam University：Natural Sciences，2004，31（4）：10－16.（In Chinese）

［14］CHEN J.Algorithmic graph embeddings［J］.Lecture Notes in Computer Science，1975，959（S）：151－160.

［15］AKLEMAN E，CHEN J Gross.Extended graph rotation systems as a model for cyclic weaving on orientable surfaces［J］.Computer Science ＆Engineering，2009，9（5）：52－57.

［16］AKLEMAN Ergun，CHEN Jianer.Cyclic plain-weaving on polygonal mesh surfaces with graph rotation systems ［C］／／Proceeding of SIGGRAPH＇09ACM SIGGRAPH 2009Papers.ACM，2009：78－83.

［17］费耀平，陈松乔，李敏.二维流形建模系统的拓扑有效性测试算法［J］.计算机辅助设计与图形学学报，2011，23（8）：1337－1348.

FEI Yao-ping，CHEN Song－qiao，LI Min.On testing topological validity for manifold modeling systems［J］.Journal of Computer-Aided Design ＆Computer Graphics，2011，23（8）：1337－1348.（In Chinese）

Research on the Complete Operation Set of Modeling 2-Manifold Mesh

FEI Yao-ping，CHEN Jian-er，CHEN Song－qiao，LI Min†
（School of Information Science and Engineering，Central South Univ，Changsha，Hunan 410083，China）

Most current modeling systems do not guarantee the 2-manifold structures and may generate non-manifold structures.In this paper，a new vertex-based representation for mesh structures was proposed，and a formal proof was given to show that this representation characterizes precisely 2-manifold structures.It has been shown that the new proposed mesh modeling operations are more intuitive，more efficient，and more user-friendly，compared with previously proposed methods in related literatures.

Euler operation；shape modeling；2-manifold；mesh-structure

TP 301

A

1674-2974（2014）05-0118-07

2013-11-01

新世纪优秀人才支持计划资助项目（NCET-12-0547）

费耀平（1959－），男，河北平山人，中南大学教授

†通讯联系人，E-mail：limin＠mail.csu.edu.cn