基于竞争ISPO 双胞支持向量回归短期负荷预测
彭显刚,王洪森
(广东工业大学自动化学院,广州510006)
电力系统负荷预测为电力系统编排调度计划、供电计划和交易计划提供基础数据。短期负荷预测对保障电力系统的安全、经济运行和电能的质量起到关键性作用[1]。“十二五”期间,随着智能电网建设的快速推进和电力市场化的进一步改革,对短期电力负荷预测速度和精度都提出了更高的要求[2]。
随着人工智能技术的高速发展,神经网络ANN(artificial neural network)[3]、模拟退火算法[4]、支持向量回归SVR(support vector regression)[5]等具有较强自学能力的预测方法被广泛应用到短期负荷预测中,取得了一定成果。支持向量回归能较好地解决过拟合、高维数和局部极小点等实际问题[6],但是SVR 模型复杂度较高,假设l 为训练样本,则训练时间为O(l3)[7]。同时,支持向量回归的超参数会严重影响算法的学习和泛化能力[8]。但是目前常用的参数优化算法如粒子群算法[9]、遗传算法[10]等存在局部最小值和收敛速度慢等缺点,优化效果有待提高。
双胞支持向量机TWSVM (twin support vector machine)方法由Jayadeva 等于2007年提出[11],之后彭新俊对其进行扩展,提出了双胞支持向量的回归算法TSVR(twin support vector regression)。传统的SVR 求解的是一个具有两组线性约束的大型的二次规划问题,而TSVR 将其分解成两个小型的二次规划问题,降低了算法规模,使训练速度提升到至少为SVR 的4 倍。智能单粒子算法ISPO(intelligent single particle optimizer)是一种新型的全局优化算法[12],具有较强的寻优能力,已经成功应用到服务开通策略的优化问题上[13]。但ISPO 算法存在参数设置问题,而且在迭代后期粒子搜索尺度不合理。本文对此加以改进,提出了竞争型智能单粒子算法CISPO(competitive intelligent single particle optimizer)优化的TSVR 负荷预测模型,通过实例仿真,分析对比ANN 模型、粒子群PSO(particle swarm optimization)优化的TSVR 模型和本文CISPO-TSVR 模型在预测速度和精度上的差异,证明了该模型的先进性。
1 TSVR 原理
TSVR 思想是寻找两个非平行的超平面方程:

分别确定ε 不敏感带的上界和下界,其中w1、w2为权值向量。假设训练样本数据为(xi,yi),xi∈Rn,yi∈R,(i = 1,2,…,l)形成训练数据矩阵为(A,Y),线性TSVR 解决的两个二次规划问题为

式中:C1、C2为惩罚参数;ε1、ε2为损失参数;ξ、η 为松弛向量;e 为相应维数的单位向量。引入拉格朗日乘子α=(α1;α2;…;αl)和β =(β1;β2;…;βl),可以将式(3)转化为其对偶形式:
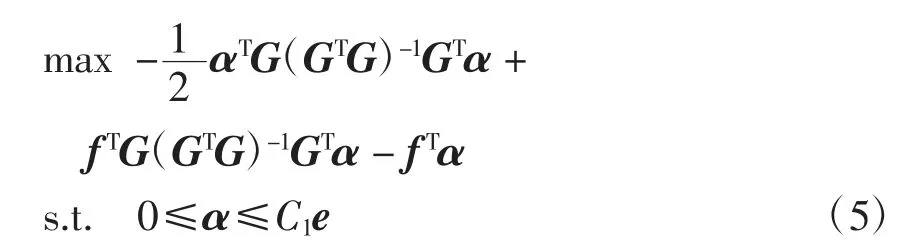
式中:G=[A e],f=Y-eε1。

同理可以得到式(4)的对偶形式:

式中,h=Y+eε2。

通过引入核函数,上下边界函数改为
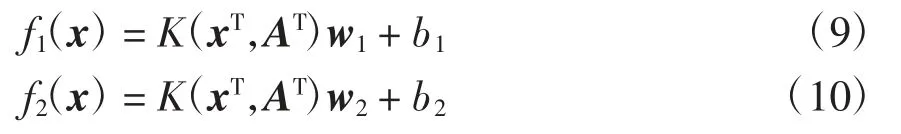
可扩展到非线性双胞支持向量回归,其原始二次规划问题为

2 竞争型智能单粒子算法
2.1 智能单粒子算法
智能单粒子优化算法由PSO 算法发展而来,其特殊之处在于算法采用单个粒子在解空间中搜索,并把位置矢量分成多个子矢量,基于子矢量对粒子进行更新。更新时,子矢量按先后顺序(从z1到zm)进行循环更新。在更新第j(1≤j≤m)个子矢量的过程中,将按以下的速度和位置更新公式迭代执行N 次:

式中:位置矢量参数L 为学习变量;随机矢量r 在[-0.5,0.5]范围内服从均匀分布;多样性因子a、升降因子p、收缩因子s 和加速度因子b(b≥1)为常数;f()为适应值函数。粒子通过每一个子矢量在解空间的智能搜索,最后找到最优解。
2.2 竞争型智能单粒子算法
智能单粒子算法对大部分标准复合测试函数都具有很强的全局搜索能力,但是算法严重依赖于搜索参数的设定,不恰当的参数设置将导致优化搜索无法有效进行,并且在实验中发现算法的多样性部分在迭代多次之后容易陷入混乱。为此,提出竞争型智能单粒子算法,使算法的参数随迭代进行自动调整,并修改算法的多样性部分,引入迭代竞争因子t,使其搜索能力更加合理。CISPO 的具体更新公式为

通过实验分析发现,CISPO 中的收缩因子s 和加速度因子b 对算法的寻优基本没有影响。根据经验设置为s=8,b=2,r 在[-1,1]范围内服从均匀分布。学习因子L 随s 收缩已经足够了,无需当其小于ε 时设为0,故将此操作取消。参数多样性因子a、升降因子p(正数为下降,负数为上升)和迭代竞争因子t 的自动更新公式为

式中:t1、t2初值均为N;N 为最大迭代次数;v为粒子最近一次找到比历史位置更优位置时的速度。
子矢量更新过程中,在迭代初期,子矢量较能找到比历史位置更优的位置,竞争因子t1占主导位置,t2不断减小,使子矢量不会因为偶尔的适应值没有改善(即t=t2)而陷入混乱。此时多样性部分[a/(1+p)t]r 下降到一定程度并逐渐变小,学习部分起主要作用,如式(16)~式(18)所示;假如在第n 次迭代中,适应值得到改善,但在第n+1次迭代中适应值没有得到改善,则最优点很有可能在第n 次迭代的位置附近,此时降低速度将有助于搜索最优点,所以将第n+2 次迭代中的L 减小到原来的1/s,由几何原理分析可知第n+2 次粒子搜索的范围应该以第n 次迭代时速度的1/2 为基础半径,如式(19)所示;当子矢量经过多次迭代后仍然无法找到更优的位置时,则粒子很有可能陷入了局部最优点,此时竞争因子t2将占主导位置,多样性部分以指数的速度迅速扩展到全局搜索,有利于找到全局最优点。
从控制理论的角度看,CISPO 算法比ISPO 算法稳定性更好,搜索能力更强,并且不存在参数的设置问题,更适合于优化多变量函数。CISPO 的算法流程如下。
步骤1 初始化粒子位置x0并计算初始适应度f(x0),参数a = amax/2(amax为子矢量取值范围),p = 1,t = N。
步骤2 初始化子矢量个数j = 1,初始学习变量L = 0
步骤3 初始子矢量迭代次数k = 1,并根据式(16)~式(23)更新子矢量的速度、位置、学习因子和多样性因子a、升降因子p 以及迭代竞争因子t。
步骤4 如果k 步骤5 如果j < m,则转到步骤2,并将j =j + 1。 使用CISPO 优化TSVR 参数包括两个关键问题:①如何选取优化组合向量x;②如何确定适应值函数。 选取Gauss 函数作为TSVR 的非线性核函数: 这样TSVR 参数为C1、C2、ε1、ε2和σ,为了使优化问题简化,可令C=C1=C2,ε=ε1=ε2,这样优化问题只包含3 个待优化量,可将每个子矢量维数取为1。本文定义(lbC,lbε,lbσ)作为待优化组合向量x,这样可以提高搜索效率,得出更稳定的优化结果[14]。 适应值函数通过引导粒子向更优的位置移动,函数值越小适应度越优,针对这个问题,定义适应度函数为 式中:tk为目标值;yk为粒子对应的(C,ε,σ)在TSVR 模型中的输出值;m 为样本数。 短期负荷预测受历史负荷、气象、温度、日期类型等因素影响,有很大的随机性。所选历史负荷与各个影响因素的相关系数如表1 所示。 表1 各个影响因素的相关系数Tab.1 Correlation coefficients of various influencial factors 可以看出,温度和日期类型对该地区负荷的影响较大,降水量则对负荷基本没有影响。另外在夏季高温累积效应也会对负荷产生较大影响,当连续4日以上温度超过25 ℃时应当考虑积温效应,积温量化公式C 可由文献[15]中的方法求得。考虑到相近日或者相同类型日在同一时刻附近的负荷点具有较大的相关性,选取历史负荷为前1、2、7 天相同时刻附近的3 个数据点。综上所述,选取的样本输入为 式中:Tmin、Tmax、Tmean、DT 分别为最低温度、最高温度、平均温度和日期类型;L(d,t)为第d 天t 时刻的待预测负荷点。 由于SCADA(supervisory control and data acquisition)系统采集负荷数据时偶尔会出现“坏点”,包括数据缺失或异变等,所以有必要对历史负荷数据进行预处理。本文采用文献[16]中的横纵向对比法来处理历史负荷数据。同时为了消除不同量纲对结果的影响,将样本数据进行归一化处理。 (1)将历史负荷数据和对应的天气数据等进行缺失补漏,异常修正和归一化处理后,根据式(26)形成每个样本的输入向量xi,输出为对应日的负荷yi,取预测日前一个月的数据作为训练样本集{(xi,yi),i=1,2,…,N}。 (2)初始化TSVR 相关参数,包括平衡因子C,损失函数ε,核参数σ,构建初始粒子(lbC,lbε,lbσ)。 (3)初始化CISPO 算法参数,多样性因子a 设置为子矢量最大尺度的1/2,这样保证粒子刚开始时可以在全局区域进行搜索,升降因子p 取0,学习因子L 取0,子矢量最大迭代次数设置为30。 (4)根据适应度函数式(25)计算粒子的适应值,设置迭代次数k=1,算法开始迭代。 (5)根据式(16)~式(23)更新粒子速度、位置、学习因子以及多样性因子等,k=k+1,如果k≤N,则继续执行第(5)步,否则跳到下一步。 (6)判断是否所有子矢量完成迭代或者适应度是否达到要求,如果满足,则输出全局最优解,即最优的(lbC,lbε,lbσ),通过进一步变换就可以得到TSVR 的最优参数向量(C,ε,σ)。否则回到步骤(3),进行下一个子矢量的优化。 (7)利用得到的最优参数向量,根据式(3)和式(4)构建TSVR 预测模型进行短期负荷预测。 本文选取广东省某市电网进行研究,为了验证CISPO-TSVR 模型的预测速度和预测精度,分别使用反向传播BP(back propagation)神经网络、SVR、TSVR、PSO-TSVR 和所提出的CISPO-TSVR模型对2011年6月7日至10日,2011年12月10日至12日共7 d 进行96 点负荷预测,其中6月份需要考虑积温效应C,而12月份不考虑积温效应。SVR 和TSVR 的参数搜索范围设置为:C∈(0.001,50),ε∈(0.001,0.5),σ∈(0.001,50)。单独SVR 和TSVR 方法的参数根据经验设置为:C=3,ε = 0.03,σ = 4。软件的运行CPU 为Pentium(R)Dual-Core E6600,内存为2GB,Matlab 版本为7.11.0.582。 选取相对误差Er和均方根相对误差RMSRE作为最终评价指标。由表2 可以看出,CISPO-TSVR法的均方根相对误差比BP-ANN 法低3.33%,说明采用结构风险最小化原则的TSVR 法具备较强的推广能力,对于解决小样本问题有绝对的优势。TSVR 法与SVR 法的均方根相对误差相差不大,TSVR 法略有优势,但是在平均耗时上SVR 法为16.95 s,TSVR 法仅为4.38 s,仅为SVR 法的1/4 左右,说明TSVR 法具有更高的训练效率。 表2 预测误差分析表Tab.2 Analysis results of forecasting error% 选取2011年12月12日的迭代曲线作为代表对两种优化算法的性能进行分析,如图1 所示,可知PSO-TSVR 法在前期适应值的改善速度要比CISPO-TSVR 法快,这是由于PSO 是基于种群中所有粒子位置进行寻优的,而CISPO 是基于子矢量的位置进行调整的,假如某一子矢量对适应值的影响相对较小或者该子矢量初始化时已经处于较好位置,则会出现迭代过程中的某段时间内适应度暂时的变化较慢。但是,从整个迭代曲线容易看出,CISPO 算法无论是收敛速度还是收敛精度都要比PSO 算法有绝对的优势。因此,由实验结果可知,基于竞争型智能单粒子优化的双胞支持向量回归模型对比其他预测模型具有更高的预测速度和预测精度。 图1 PSO-TSVR 和CISPO-TSVR 迭代曲线Fig.1 Iterative curves of PSO-TSVR and CISPO-TSVR 本文提出基于竞争型智能单粒子优化的双胞支持向量回归短期负荷预测模型。从实验结果分析,可得出以下结论。 (1)双胞支持向量回归算法由于求解的是两个较小规模的二次规划问题,使它的训练速度要比传统的支持向量回归有显著的提高。 (2)竞争型智能单粒子算法通过对智能单粒子算法进行取长补短,有效解决了参数设置问题,加强全局搜索能力,使算法寻优能力更强,收敛精度更高。构建的CISPO-TSVR 短期负荷预测模型结合了两者的优点。实验结果表明,与BP 神经网络、SVR、TSVR 和PSO-TSVR 等算法进行对比,本文方法不仅训练速度快,而且预测精度较高,验证了该算法的先进性。 [1]康重庆,夏清,刘梅.电力系统负荷预测[M].北京:中国电力出版社,2007. [2]曾鸣,吕春泉,田廓,等(Zeng Ming,Lü Chunquan,Tian Kuo,et al).基于细菌群落趋药性优化的最小二乘支持向量机短期负荷预测方法(Least squares-support vector machine load forecasting approach optimized by bacterial colony chemotaxis method)[J]. 中国电机工程学报(Proceedings of the CSEE),2011,31(34):93-99. [3]赵菁,许克明(Zhao Jing,Xu Keming).神经网络和模糊理论在短期负荷预测中的应用(Application of neural network and fuzzy theory in short-term load forecasting)[J].电力系统及其自动化学报(Proceedings of the CSUEPSA),2010,22(3):129-133. [4]廖立,忻建华,叶春(Liao Li,Xin Jianhua,Ye Chun). 模拟退火算法及其在短期负荷预测中应用(Application of simulated annealing algorithm to short-term load forecast)[J].电力自动化设备(Electric Power Automation Equipment),2004,24(4):30-33. [5]Niu Dongxiao,Wang Yongli. A new modal to short-term power load forecasting combining chaotic time series and SVM[C]//First Asian Conference on Intelligent Information and Database Systems.Dong Hoi,Vietnam:2009. [6]张学工(Zhang Xuegong).关于统计学习理论与支持向量机(Introduction to statistical learning theory and support vector machines)[J]. 自动化学报(Acta Automatica Sinica),2000,26(1):32-42. [7]Peng Xinjun. TSVR:an efficient twin support vector machine for regression[J]. Neural Networks,2010,23(3):365-372. [8]杨国建,杨镜非,童开蒙,等(Yang Guojian,Yang Jingfei,Tong Kaimeng,et al).短期负荷预测的支持向量机参数选择方法(Parameter selection of support vector machine for short-term load forecasting)[J]. 电力系统及其自动化学报(Proceedings of the CSU-EPSA),2012,24(6):148-151. [9]王奔,冷北雪,张喜海,等(Wang Ben,Leng Beixue,Zhang Xihai,et al).支持向量机在短期负荷预测中的应用概况(Application profiles of support vector machine in short-term load forecasting)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2011,23(4):115-121. [10]吴景龙,杨淑霞,刘承水(Wu Jinglong,Yang Shuxia,Liu Chengshui).基于遗传算法优化参数的支持向量机短期负荷预测方法(Parameter selection for support vector machines based on genetic algorithms to short-term power load forecasting)[J].中南大学学报:自然科学版(Journal of Central South University:Science and Technology),2009,40(1):180-184. [11]Jayadeva,Khemchandani R,Chandra Suresh. Twin support vector machines for pattern classification [J]. IEEE Trans on Pattern Analysis and Machine Intelligence,2007,29(5):905-910. [12]纪震,周家锐,廖惠连,等(Ji Zhen,Zhou Jiarui,Liao Huilian,et al).智能单粒子优化算法(A novel intelligent single particle optimizer)[J].计算机学报(Chinese Journal of Computers),2010,33(3):556-561. [13]张卫,潘晓弘,祝勇,等(Zhang Wei,Pan Xiaohong,Zhu Yong,et al).基于智能单粒子优化的制造服务开通策略(Manufacturing service open strategy based on intelligent single particle optimization)[J]. 计算机集成制造系统(Computer Integrated Manufacturing Systems),2011,17(9):2079-2084. [14]Keerthi S S,Lin Chih-Jen. Asymptotic behaviors of support vector machines with Gaussian kernel[J].Neural Computation,2003,15(7):1667-1689. [15]蒋建东,程志豪,朱明嘉(Jiang Jiandong,Cheng Zhihao,Zhu Mingjia).考虑积温效应的短期负荷组合预测方法(Combined short-term load forecast with accumulated temperature effect)[J].电力自动化设备(Electric Power Automation Equipment),2011,31(10):28-31. [16]陈亚红,穆钢,段方丽(Chen Yahong,Mu Gang,Duan Fangli).短期电力负荷预报中几种异常数据的处理(Identification and management to anomalous data in shortterm load forecasting)[J].东北电力学院学报(Journal of Northeast China Institute of Electric Power Engineering),2002,22(2):1-5.3 CISPO-TSVR 的短期负荷预测模型
3.1 基于CISPO 的参数优化


3.2 样本数据选取和预处理


3.3 CISPO-TSVR 的短期负荷预测流程
4 应用实例
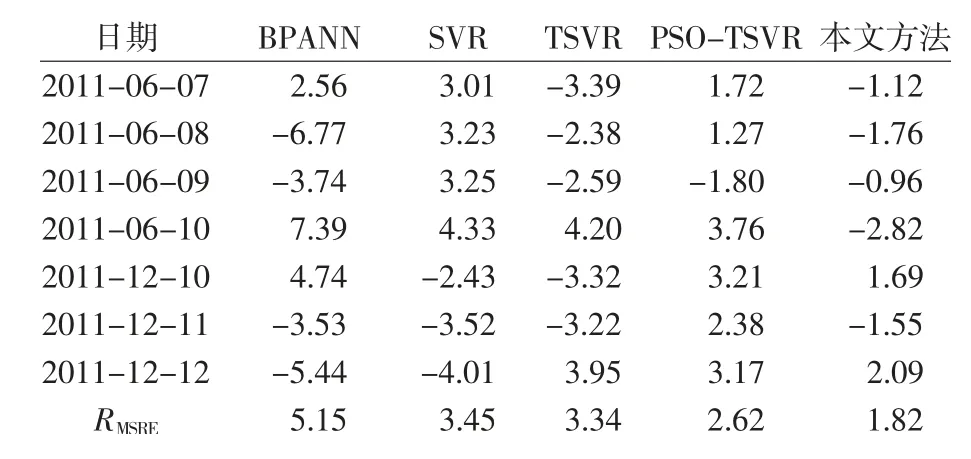

5 结论

