发电机励磁与TCSC 的非线性协调控制

杨培宏，刘文颖，魏毅立，张继红，赵 岩

（1.内蒙古科技大学信息工程学院，包头014010；2.华北电力大学电气与电子工程学院，北京102206）

可控串联补偿TCSC（thysistor controlled series compensation） 作为柔性交流输电系统FACTS（flexible AC transmission system）家族中重要的成员之一，在提高电力系统暂态稳定和电力系统阻尼比等方面发挥着重要作用，并成功地应用在实际工程中[1-6]。特别文献[5]是在实际运行含TCSC 的伊冯输电系统进行了分析计算，指出采用离散控制策略，能大大提高满足暂稳约束的联络线路传输能力。

发电机励磁控制在电力系统稳定控制中一直发挥着重要作用，已被公认为是改善电力系统稳定特性最经济、最有效的措施[7-11]。

为此将发电机励磁系统的非线性控制与新型的FACTS 控制器进行协调控制以改善电力系统的稳定性具有一定的研究价值，文献[12]基于最优变目标控制理论对励磁系统与TCSC 进行协调控制，该方法能够有效地提高系统阻尼，改善系统的稳定性。文献[13]提出了能够抗干扰的鲁棒非线性协调控制规律，该方法是通过耗散不等式的递推设计，能够有效地抑制干扰的影响，提高电力系统的稳定性。文献[14]利用改进的遗传算法对电力系统中的附加励磁控制PSS 和TCSC 进行鲁棒分散协调控制，有效地抑制了电力系统的低频振荡，提高了电力系统的阻尼比。文献[15]结合逆方法和滑模变结构方法设计了一种静止无功补偿器和发电机励磁的协调控制器，所设计的协调控制器能有效地提高电力系统的暂态稳定性并可保持机端电压恒定。

本文利用非线性系统的微分几何理论，将含有TCSC 的单机无穷大系统非线性数学模型精确线性化，采用滑模控制理论对线性化系统进行协调控制，进而得出整个系统的协调控制规律。

1 数学模型

基于晶闸管控制的串联电容器的单机无穷大系统原理接线如图1 所示，其中TCSC 安装在输电线路中点。

给定如下假设：不考虑调速系统的调节作用，即Pm为常数；忽略定子回路电阻和转子阻尼绕组的影响；TCSC 采用可变电抗模型，即用一阶惯性环节表示[16]。

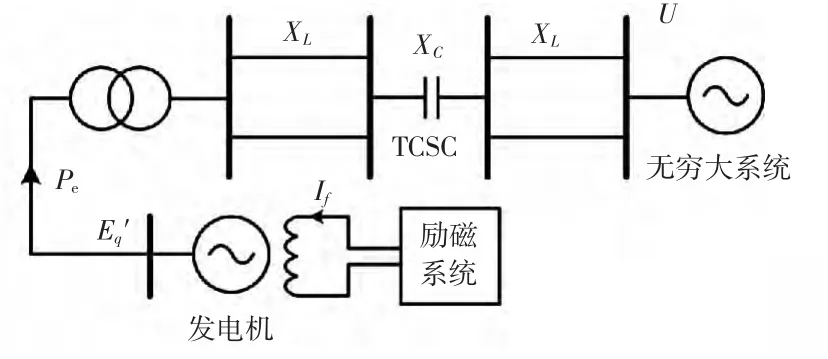
图1 含TCSC 的单机无穷大系统原理接线Fig.1 Single-machine-infinite-bus power systems with TCSC

针对图1 所示的单机无穷大系统可知，发电机系统的数学模型可表示为

式中：δ 为发电机功角；ω 为角速度；ω0为额定角速度；Pm为发电机机械功率；Pe为发电机电磁功率；T为惯性时间常数；D 为阻尼系数；Eq′为发电机暂态电势；uf为发电机励磁控制输入；Td0为励磁绕组时间常数为定子闭路时励磁绕组时间常数；Us为无穷大系统母线电压。

TCSC 的动态方程可写为

式中：XC为可控串联补偿的等值电抗；XC0为可控串联补偿的初始电抗；TC为可控串联补偿的时间常数；uC为可控串联补偿的等效控制量。

式（1）中的发电机电磁功率满足关系

由式（1）～（3）可得

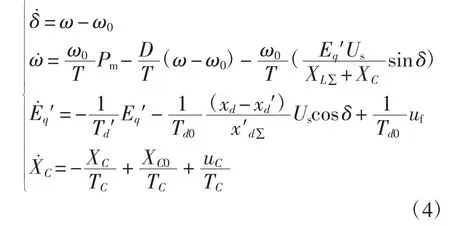
2 非线性控制系统的线性化

精确线性化是通过严格的状态变换与反馈变换进行的，变换的过程中没有忽略任何高价非线性项，因而线性化的过程是精确的，而不是借助于动态系统的线性近似[17]。

选取状态变量

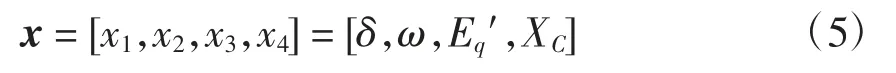
则式（4）可表示为双输入双输出放射非线性系统的形式为

式中：x =（x1，x2，x3，x4）T=（δ，ω，Eq′，XC）T；g1=（0 0 1/Td00）T；g2=（0 0 0 1/TC）T；y =（y1 y2）T=（h1 h2）T；u1=uf；u2=uC；y1=h1=δ；y2= h2= Pe；f（x）= [f1（x）f2（x）f3（x）f4（x）]T=

要想对式（6）实现精确反馈线性化，需对其进行验证，即判断系统的相对阶。为此，对式（6）的输出h1和h2计算各阶李导数为

该控制系统的自由阶集合为

又r=r1+r2=4，即系统的自由阶总数等于其阶数，所以精确线性化有解。

又有

将式（17）化为Brunovsky 标准型，即

系统输出方程为

则系统可写成

为此，构造的状态反馈为

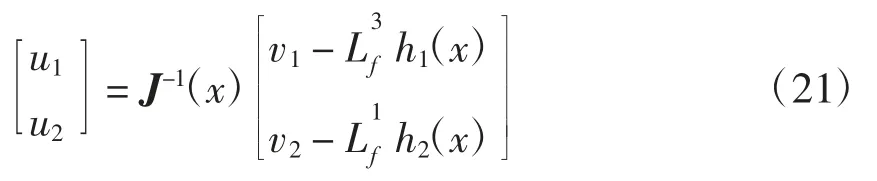
式中：

取

则

3 协调控制器设计

针对运行参数的不确定性，采用滑模控制理论对发电机励磁系统与TCSC 进行协调控制，具体方法如下。

将式（20）所示的线性化系统分为两个独立的子系统进行研究，即

分别对两个子系统进行滑模控制设计。

先对第1 个系统进行设计，取滑模函数为

则滑模动态方程为

其中，c1、c2与滑模面的极点有关，而此极点正是发电机运动的期望极点。

同理可知第1 个系统的滑模函数为

为此，滑模控制中切换函数为

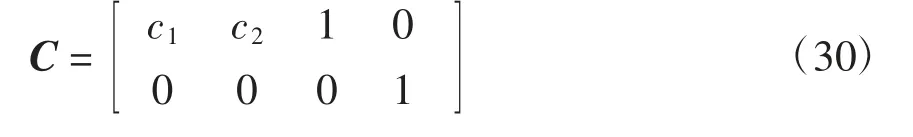
选取趋近律控制为

其中：ε=diag[ε1ε2ε3]，εi＞0；sat（s/Δ）=[sat（s1/Δ）sat（s2/Δ）sat（s2/Δ）]T；f（s）=[k1s1k2s2k3s3]T。于是有

从而可得控制输入

将式（33）带入式（21）中即可得出整个系统的控制输入。

4 仿真计算

仿真系统选取如图1 所示的单机无穷大系统，发电机及网络归一参数为xd=1.8，xd′=0.3，Td0=8，Td′ = 3，T = 13，XL= 0.04，XT = 0.016 6，XTCSC0 =-0.03，ε1=ε2=0.15，ε3=0.15，k1=5，k2=k3=1，c1=18，c2=10，Δ=0.2，TCSC 的电抗变化范围XTCSC∈[-0.1，0.1]。

为了验证本文设计的最优协调控制规律，在发电机励磁电压幅值加5%的阶跃扰动信号，时域仿真结果如图2 所示。

图2 发电机转速振荡曲线Fig.2 Oslillation Curves of the generator speed

从图2 可看出，采用最优协调控制后抑制振荡的效果很明显优于优化前。

为了充分验证该方法的有效性，设置较为严重的扰动方式并与常规PSS 进行比较，仿真时考虑以下两种情况进行扰动方式设置。PSS 的参数为：k = 28，Tq= 4，T1= 0.65，T2= 0.2，T3= 0. 853，T4=0.2，Vsmax=0.2，Vsmin=-0.2。

TCSC 的参数设置为：KTCSC=10.0，TC=0.2

为了更好地说明发电机励磁与TCSC 的非线性最优协调控制的有效性，设计更为复杂的扰动方式，故障设置为：1 s 时输电线路一回线路发生三相接地短路故障，1.15 s 后故障切除，由单回线路供电，1.5 s 时重合闸成功，线路恢复正常运行，由双回线路继续供电，发电机的功角变化和功率变化曲线如图3、4 所示。

图3 发电机G 功角振荡曲线Fig.3 Power angle oslillation curves

图4 联络线路的功率振荡曲线Fig.4 Power oslillation curves of the tie line

在1 s 时双回线路一回发生三相短路故障，故障持续0.15 s 后，故障消除，在1.5 s 时断路器重合成功，继续双回线路运行，从图3 和图4 可以看出，采用最优协调控制后，采用发电机励磁与TCSC 最优协调控制，发电机的功角和联络线路功率响应很快，4 s 左右就达到了稳定状态，与常规PSS 相比较，最优协调控制下，振荡幅度较小且振荡次数较少，明显地改善了系统的稳定性，具有较好的鲁棒性和自适应能力。

5 结语

本文研究了TCSC 和发电机励磁系统的协调控制问题。利用非线性系统的微分几何理论，对含有TCSC 的单机无穷大系统的非线性数学模型精确线性化。针对线性化模型，采用滑模控制理论获得整个系统的协调控制规律。从单机无穷大系统的仿真结果曲线可以看出，所设计的协调控制器具有良好的抗干扰能力，而且有效地提高了电力系统的稳定性。

[1]朱旭凯，周孝信，田芳，等（Zhu Xukai，Zhou Xiaoxin，Tian Fang，et al）.基于本地测量信号的TCSC 抑制次同步振荡附加控制（Supplementary damping control of TCSC for subsynchronous oscillation based on local measured signal）[J].电力系统自动化（Automation of Electric Power Systems），2011，35（23）：22-25.

[2]吴熙，蒋平，胡弢（Wu Xi，Jiang Ping，Hu Tao）.电力系统稳定器对次同步振荡的影响及其机制研究（Impact of power system stabilizer on subsynchronos oscillation and its mechanism）[J]. 中国电机工程学报（Proceedings of the CSEE），2011，31（22）：56-63.

[3]Yang N，Liu Q，McCalley J D. TCSC controller design for damping interarea oscillations[J]. IEEE Trans on Power Systems，1998，13（4）：1304-1310.

[4]林卫星，张星，李刚，等（Lin Weixing，Zhang Xing，Li Gang，et al）.一种新型的FACTS 控制设备实验与性能测试平台（A novel platform for experimenting and testing FACTS controllers）[J]. 电工技术学报（Transactions of China Electrotechnical Society），2012，27（3）：227-232.

[5]张颖（Zhang Ying）.考虑暂稳约束下含TCSC 联络线的传输能力（Transmission ability study of tie-line mounted TCSC considering transient ability const）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2011，23（3）：127-130，149.

[6]王延鹏，蔡兴国（Wang Yanpeng，Cai Xingguo）. 确定TCSC 安装位置和安装容量的方法（Approach to determine the optimal location and parameter setting of TCSC）[J].电力系统及其自动化学报（Proceedings of the CSUEPSA），2010，22（2）：48-53.

[7]石方，王杰（Shi Fang，Wang Jie）.伪广义哈密顿理论及其在多机电力系统非线性励磁控制中的应用（Pseudogeneralized Hamiltonian theory and its application to multi-machine power system nonlinear excitation control）[J]. 中国电机工程学报（Proceedings of the CSEE），2011，31（19）：67-74.

[8]李康，王杰（Li Kang，Wang Jie）. 电池储能系统与发电机励磁的多指标非线性协调控制（Multi-index nonlinear coordinated control for battery energy storage system and generator excitation）[J].电力系统保护与控制（Power System Protection and Control，），2011，39（13）：25-31.

[9]李啸骢，谷立基，徐俊华，等（Li Xiaocong，Gu Liji，Xu Junhua，et al）.基于模糊协调控制策略的同步发电机励磁系统研究（Study on the synchronous excitation system based on the strategy of fuzzy coordinated control）[J]. 电力系统保护与控制（Power System Protection and Control），2011，39（11）：62-66.

[10]阮阳，袁荣湘（Ruan Yang，Yuan Rongxiang）. 非线性输出反馈控制的理论改进及其在电力系统励磁控制中的应用（An improvement of nonlinear output feedback control theory and its application to excitation control for power system）[J]. 中国电机工程学报（Proceedings of the CSEE），2011，31（13）：33-39.

[11]Liu Yan-Hong，Li Chun-Wen，Wang Yu-Zhen. Decentralized excitation control of multi-machine multi-load power systems using Hamiltonian function method[J].Acta Automatica Sinica，2009，35（7）：919-925.

[12]徐大鹏，李兴源，洪潮，等（Xu Dapeng，Li Xingyuan，Hong Chao，et al）.基于最优变目标策略的TCSC 与励磁系统协调控制（Coordination control between TCSC and generator excitation based on optimal variable aim strategy）[J].电网技术（Power System Technology），2008，32（21）：13-16，21.

[13]兰海，徐殿国，刘胜，等（Lan Hai，Xu Dianguo，Liu Sheng，et al）.基于耗散理论的TCSC 与励磁协调控制研究（Study on dissipative theory in coordinated control for TCSC and generator excitation）[J]. 系 统 仿 真 学 报（Journal of System Simulation），2006，18（8）：2230-2234.

[14]杨培宏，刘文颖，张继红（Yang Peihong，Liu Wenying，Zhang Jihong）.PSS 和TCSC 联合抑制互联电网低频振荡（Restraining low frequency oscillation of interconnected power grid using PSS and TCSC）[J].电力系统保护与控制（Power System Protection and Control），2011，39（12）：11-16.

[15]邹德虎，王宝华（Zou Dehu，Wang Baohua）.SVC 与发电机励磁的逆推Terminal 滑模协调控制（Backstepping terminal sliding mode coordinated control for SVC and generator excitation）[J].电网技术（Power System Technology），2011，35（4）：108-111.

[16]Zhou X X，Liang J. Nonlinear adaptive control of TCSC to improve the performance of power systems [J]. IEE Proceedings-Generation，Transmission and Distribution，1999，146（3）：301-305.

[17]卢强，孙元章.电力系统非线性控制[M].北京：科学出版社，1993.