基于模糊理论的地下变电站LCC 估算

杜 渐，顾 洁，秦 杰，张 怡

（1.上海交通大学电力传输与功率交换控制教育部重点实验室，上海200240；2.上海交通大学电气工程系，上海200240；3.上海电力设计院有限公司，上海200025）

随着我国城市规模的不断扩大和供电负荷的日益增高，在市中心建设大电压等级（110 kV、220 kV 或500 kV）的地下变电站已逐渐成为一种趋势。然而，地下变电站在建设和运行的过程中不得不面临许多难题，例如规划选址难、征地拆迁费用大、安全环保要求高等[1-3]。为了提高地下变电站的土地和资金利用率，更好地指导变电站的规划建设与运行管理，资产全寿命周期管理LCAM（lifecycle asset management）的理念和方法已越来越多地得到应用[4-6]，对地下变电站进行全寿命周期成本LCC（life-cycle cost）的估算无疑是其中的核心和关键。

传统的LCC 估算方法主要包括参数估算法、工程估算法、类比估算法、神经网络估算法和作业成本估算法等[7-8]，这些方法大都需要较为详细的投资及运行数据，而要完整地收集这些数据往往非常困难。同时，变电站的建设和运行是一项复杂的系统工程，其寿命周期很长（服役年限一般能达到30～50 a），这期间的建设投入、运行维护和停电损失等成本都具有很大的不确定性[9-11]。

针对这种情况，本文将模糊理论引入LCC 的估算过程，在分析地下变电站LCC 构成的基础上搭建起估算模型，应用模糊平滑法对LCC 分量进行预测，并进一步将预测结果模糊化，根据模糊函数的运算规则得到最终的估算结果。这样的估算结果更加合理可信，为地下变电站工程的项目评标和成本优化提供了有价值的参考。

1 地下变电站LCC 估算模型

地下变电站的LCC 是指地下变电站经济寿命周期内所支付的总费用，由以下几部分组成。

（1）一次投资成本CI，指地下变电站在建设和调试期间的所有初始投资，包括设备购置费CI1、安装工程费CI2、建筑工程费CI3、其他费用CI4和动态费用CI5[12]。

（2）运行成本CO，指地下变电站在运行期间所花费的日常费用，按年计算，包括能耗费CO1、维保费CO2和保险费CO3。

（3）检修成本CM，指地下变电站对其设备和设施进行定期维护、修缮所产生的费用，分为小修费用CM1和大修费用CM2两类。

（4）故障成本CF，指地下变电站在运行期间因设备或设施故障而产生的成本，按年计算，包括中断供电惩罚成本CF1和故障设备修复成本CF2两部分[13]。

（5）报废成本CD，指地下变电站在寿命周期结束后的设备回收收入和现场清理费用的财务计算值，分为设备残值CD1（作为成本时为负值）和设备拆除费CD2两部分。

此外，由于变电站的寿命周期较长，因此在进行LCC 估算时必须考虑资金的时间价值，即利用基准折现率将寿命周期内的全部成本折算成初始投资年限的资金现值。

基于上述分析，将CO 和CD 两项成本按照CI进行定额折算，得到地下变电站LCC 估算模型为

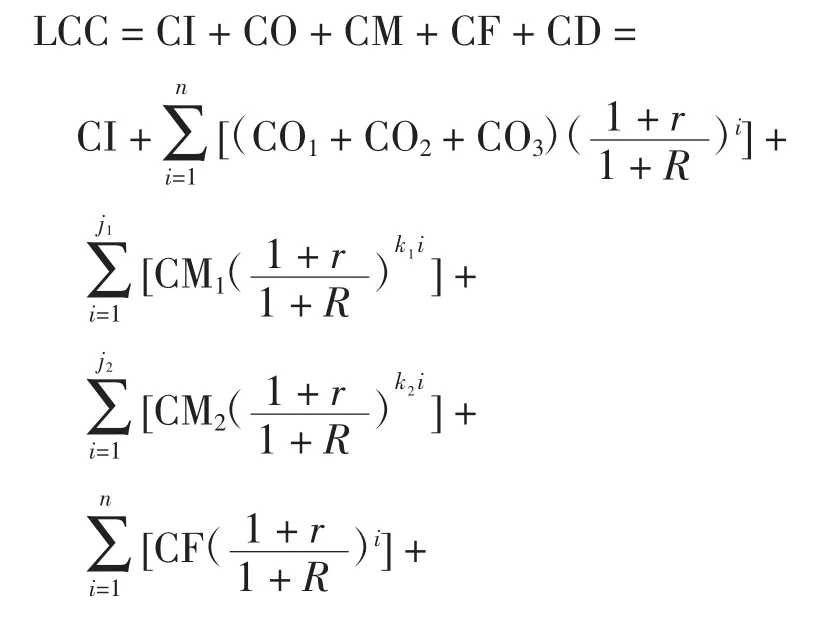
式中：r 为通货膨胀率；R 为年利率；n 为地下变电站的运行年数；j1为运行年限中小修的总次数；j2为运行年限中大修的总次数；SN为地下变电站各主变的额定容量之和，MW；α 为主变负载率，3 台主变时取为0.67，两台主变时取为0.5；Tmax为年最大负荷利用小时，参考有关资料，华东地区可统一取为3 500 h；Pe为平均购电电价，取为0.04 万元/（MW·h）；γ1为变电站耗电量占输电量的比例折算系数，取为2%；γ2为CO2占CI1的比例折算系数，取为1.5%；γ3为CO3占CI1的比例折算系数，取为0.25%；γ4为CD1占CI1的比例折算系数，取为5%；γ5为CD2占CI2的比例折算系数，取为50%。

由式（1）可知，如何准确地得到CI（包括CI1和CI2）和CF 的估算值是整个估算模型的关键。如果按照CI 和CF 的构成进行详细的量化计算，需要大量的统计数据，并且由于许多不确定因素的影响，计算的精确度难以得到保证。鉴于此，本文基于模糊理论中的贴近度概念，结合经典的指数平滑预测法提出模糊平滑的方法，利用同地区已投运的典型地下变电站的相关数据，对新建地下变电站的CI、CI1、CI2和CF 分别进行类比预测。

2 模糊理论在地下变电站LCC 估算中的应用

2.1 模糊理论简介

模糊理论（fuzzy theory）是在美国Zadeh（扎德）教授于1965年创立的模糊集合理论的数学基础上发展起来的，主要包括模糊集合理论、模糊逻辑、模糊推理和模糊控制等方面的内容[14]。

模糊集合是模糊理论的基础和核心，是经典集合的推广和拓展。设论域X 上有模糊集

式中，μA（x）称为A 的模糊隶属函数（简称模糊函数），模糊集A 通过其模糊函数进行刻画。μA（x）的取值越大，说明x 属于X 的程度越大；μA（x）=1，表示x 完全属于X；μA（x）=0，则表示x 完全不属于X。

如同向量空间中的两个点，可以考察它们靠近的程度，对某个论域上的两个模糊集合，也需要考虑它们的贴近程度。设A、B 是论域X 上的两个模糊集，可将它们的贴近度定义为

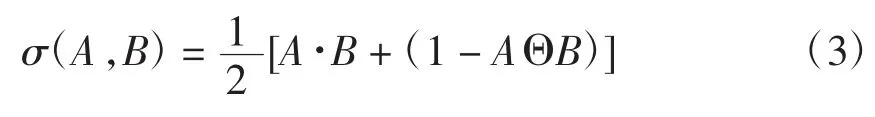
其中：

它们分别叫做A、B 的“内积”和“外积”。这里，符号“∪”表示取最大值，“∩”表示取最小值[14]。

2.2 应用模糊平滑法估算LCC 分量

2.2.1 基本思路

在进行新建地下变电站的CI（包括CI1和CI2）和CF 的估算时，根据指数平滑理论，选取3 个与新建地下变电站最为相似的典型地下变电站，并将平滑指数设定为相应的贴近度，得到的估算公式[15-16]为

式中：E*为新建地下变电站LCC 分量（CI 或CF）的估算值；E1、E2、E3为典型地下变电站LCC 分量的实际值；σ1、σ2、σ3分别为各典型地下变电站与新建地下变电站的贴近度；λ 为调整系数。

为了得到两个变电站之间的贴近度，需首先根据待估算的LCC 分量的特点，确定相应的特征因素集。接着，分别设定每个变电站各特征因素的模糊隶属度，构建各自的模糊特征集合，再根据式（3），求得两个模糊集合之间的贴近度，即为两个变电站的贴近度。需要注意的是，估算不同的LCC分量时，由于特征因素集不同，同样两个变电站之间的贴近度却不一定相同。

确定隶属度之后，可进一步求得式（4）中的调整系数λ，其经验公式为

式中：m 为特征因素的个数；TS为新建变电站各特

征因素的隶属度之和，称为模糊关系系数；Tσ1、Tσ2和Tσ3分别为与贴近度σ1、σ2和σ3对应的典型变电站的模糊关系系数。

2.2.2 隶属度的优化调整

地下变电站各特征因素的模糊隶属度决定了变电站之间贴近度的大小，因此隶属度的设定是估算结果精确与否的关键，需要在估算的过程中对其进行不断地调整。在设定典型地下变电站的隶属度初值后，用式（4）对典型地下变电站的LCC分量进行估算检验，所有变电站的检验误差小于等于10%视为通过，否则需要对隶属度进行优化调整。隶属度的调整可抽象成线性最优化问题，即

式中：T 为所有典型地下变电站各特征因素的隶属度组成的n × m 矩阵；n 为典型地下变电站的个数；m 为特征因素的个数；ei为第i 个典型地下变电站的检验误差，等于其估算值Ei*与实际值Ei差值的绝对值与实际值Ei的比例；rc为惩罚因子，当ei≤10%时，rc=1，当ei>10%时，rc=10 000；tij为隶属度矩阵T 的元素，表示第i 个典型地下变电站的第j 个特征因素的隶属度，tij0为tij的初值。

2.2.3 估算流程

典型地下变电站的隶属度检验通过后，需要根据新建地下变电站的情况，设定其特征因素的隶属度初值。接着，利用式（4）进行新建地下变电站的成本估算，并将估算结果作为已知，重新对各典型地下变电站进行估算检验，直到检验通过，得到相应的估算结果。这样，将应用模糊平滑法估算地下变电站LCC 分量的流程总结如图1 所示。

2.3 LCC 估算结果模糊化

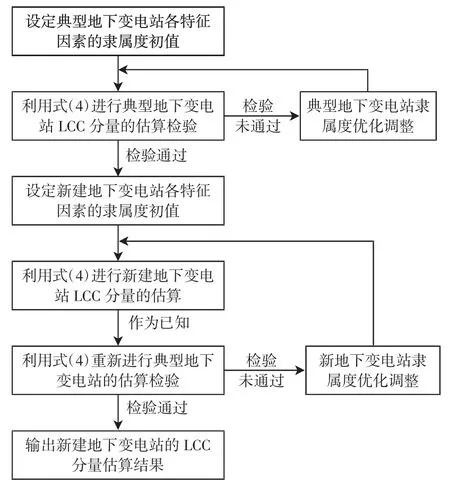
图1 模糊平滑法估算流程Fig.1 Estimation process using the fuzzy smooth method

由第2.2 节的论述可见，应用模糊平滑法得到的估算结果是基于优化调整后的隶属度得到的，而隶属度优化调整的过程本身并不具有确定性。基于模糊理论的思想，可以对估算过程稍加改进，用典型地下变电站各特征因素的初始隶属度和优化隶属度，分别对新建地下变电站的LCC 分量进行估算，并利用这两个结果构建隶属度函数，将原本单一的预测结果模糊化。模糊化的过程可采用多种形式来构建隶属度函数，本文根据变电站LCC 的特点，采用较为典型的“三角形”函数，具体构建过程如下。

设某LCC 分量由初始隶属度得到的估算结果为C1，由优化隶属度得到的估算结果为C2，以C2为中心，当C1＜C2时，取估算结果C3使得C3-C2=C2-C1，估算结果在区间[C1，C3]上取值；当C1＞C2时，取估算结果C3使得C2-C3=C1-C2，估算结果在区间[C3，C1]上取值。由于优化隶属度的估算结果C2通过了精确度检验，更加可信，故设定其隶属度为1；初始隶属度的估算结果C1没有通过精确度检验，作为参考，设定其隶属度为0。论域中其他元素的隶属度分别由一条递增和一条递减的一次函数取值而得，函数图像总体上呈现一个对称的“三角形”形状，故可称为“三角形”隶属度函数，如图2所示。

对于CM 的估算结果，可按照类似的方法写成模糊函数的形式。这样，模糊化的估算结果实际上是一个模糊集合，可以用加波浪线的形式表征其模糊性，例如CI 的模糊估算值用表示。在分别得到后，就可以代入式（1）的模型，按照模糊函数的运算规则得到最终的LCC 模糊估算值。

图2 “三角形”隶属度函数Fig.2 “Triangle”membership degree function

3 算例分析

收集我国华东地区五所110～220 kV 典型地下变电站（甲、乙、丙、丁、戊）的LCC 数据作为参考，对该地区新建的某座110 kV 地下变电站S 进行LCC 模糊估算的实例应用。

3.1 LCC 分量的模糊平滑估算

应用模糊平滑法对新建地下变电站S 的CI、CI1、CI2和CF 进行估算。下面以CI 为例说明估算过程，设定CI 的6 个特征因素分别为：电压等级、主变容量、主接线及设备选型、建筑面积、站区用地面积及土地性质、通风给排水要求。

1）设定典型地下变电站CI 的隶属度初值

设定隶属度初值时，首先要在同类因素中找出比较的基准，一般选工程较复杂、费用较高的因素水平为基准，规定其隶属度为1，将其他变电站该因素的水平分别与这个基准水平相比较，在闭区间[0，1]中根据主观经验赋予隶属度值。初值设定情况如表1 所示。

2）典型地下变电站CI 的估算检验与隶属度优化调整

利用表1 中的隶属度初值，分别对5 所典型地下变电站进行CI 的估算检验。

以地下变电站甲为例，与其贴近度排名前3的依次为

表1 典型地下变电站CI 的隶属度初值Tab.1 Initial values of the membership degree of typical underground substations′CI

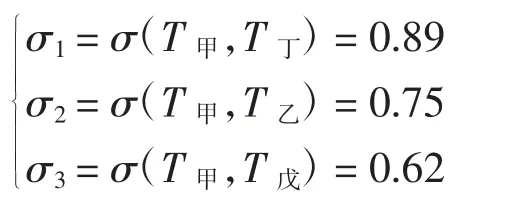
对应地下变电站的CI 依次为

根据式（5）求得调整系数为

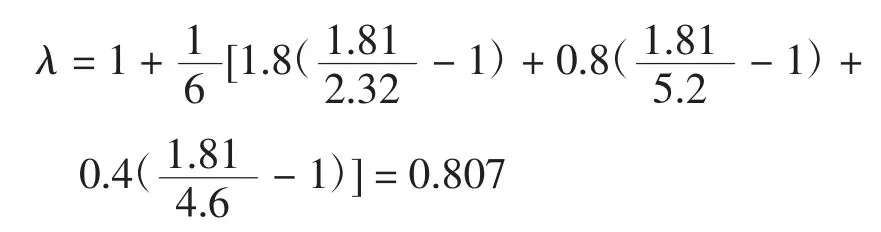
按照同样的方法对其他4 个地下变电站进行估算检验，其中乙、丙、戊3 个变电站的检验误差都大于10%，均没有通过检验。因此，需要按照第2.2.2 节提出的优化模型，对表1 中的隶属度初值进行优化调整，得到调整结果如表2 所示。

隶属度调整后，所有典型地下变电站的CI 估算结果都通过了检验，且其检验误差之和Σei仅为12.6%，从而验证了隶属度调整的效果。由此，可将表2 中的结果作为典型地下变电站CI 的最终隶属度。

表2 典型地下变电站CI 隶属度优化调整结果Tab.2 Optimized adjustment results of the membership degree of typical underground substations′CI

3）设定新建地下变电站CI 的隶属度初值并进行CI 的估算

新建地下变电站S 的电压等级为110 kV，安装3 台50 MVA 主变压器，总容量为150 MVA。主接线方面，110 kV 侧为线路变压器组接线，3 回进线，合资GIS 设备；10 kV 侧单母六分段，24 回出线，国产GIS 设备。另外，站区位于城市中心，地段优，站区拟用地面积为2 810 m2，政府给予一定的买地补贴。建筑工程方面，规划3 层地下建筑，总建筑面积为1 726 m2。通风和给排水要求中等，与一般110 kV 地下站类似。根据上述信息，参照表1和表2 中的数据，设定地下变电站S 的隶属度初值如表3 所示。

表3 地下变电站S 的CI 隶属度初值Tab.3 Initial values of the membership degree of underground substation S′s CI

用式（4）对地下变电站S 的CI 进行估算，估算结果为12 709.49 万元。

4）重新进行典型地下变电站CI 的估算检验

将地下变电站S 的CI 估算结果作为已知，再次对各典型地下变电站进行CI 的估算检验。检验结果显示，各站CI 的估算误差均在10%以内，因此12 709.49 万元的估算结果是可靠的。

同理对CI1、CI2和CF 进行模糊平滑估算，特征因素设定和估算结果如表4 所示。

表4 地下变电站S 的LCC 分量估算结果Tab.4 Estimation results of underground substation S′s LCC components

LCC 分量特征因素的设定，尤其是CI（包括CI1和CI2）的“站区用地面积及土地性质”、“通风给排水要求”、“吊装难度”等特征因素，充分反映了地下变电站的特点，而这些因素也正是左右地下变电站LCC 大小的关键。

3.2 LCC 模糊估算结果

根据第2.3 节的方法，对表4 中4 个LCC 分量的估算结果进行模糊化，如表5 所示。

另外，根据文献[17]中的规定，按照变电站的容量和所处地域，计算得到地下变电站S 每次检修的标准成本CMstd为61.56 万元，即认为每次小修的成本CM1和每次大修的成本CM2之和为61.56 万元。设该变电站的运行年限n 为30 a，采用8 a 一小修，15 a 一大修的检修方式，认为小修成本CM1和标准检修成本CMstd的比例β 是一定的，在[0.04，0.06]的区间上取值。同样用“三角形”隶属度函数对CM1和CM2进行模糊化，当β=0.05 时，隶属度取为1，当β=0.04 或0.06 时，隶属度取为0，得到模糊估算结果如表6 所示。

其中：

表6 地下变电站S 的CM 模糊估算结果Tab.6 Fuzzy estimation results of underground substation S′s CM

隶属度函数μLCC（x）的图像如图3 所示。

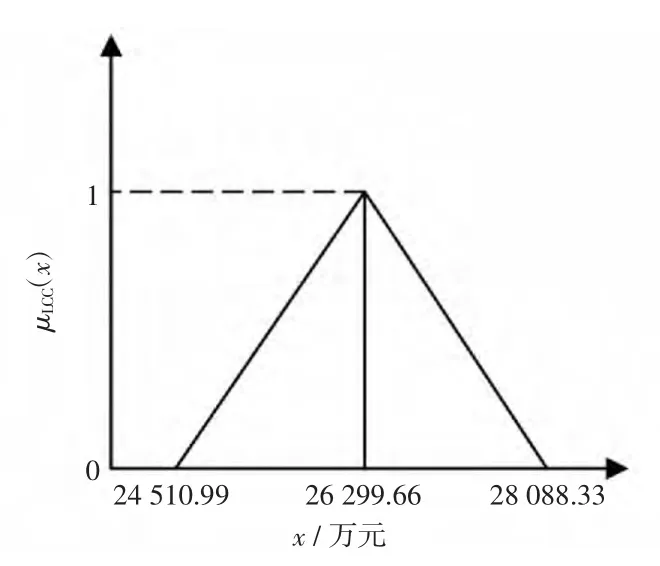
图3 的隶属度函数μLC（Cx）Fig.3 Membership degree function μLC（Cx）of

由以上结果可知，基于模糊理论的地下变电站LCC 估算充分利用了典型地下变电站的已知数据，为新建地下变电站的LCC 估算提供了有效的参考，这种类比估算的方法相比于详细的量化计算具有更强的可操作性。同时，以模糊集合的形式得到估算结果，很好地体现了变电站LCC 的不确定性，合理地给出了LCC 的估算区间和取值可信度，较以往的估算方法更具参考价值。另一方面，算例估算结果中高达几千万元的成本区间，也充分说明了LCAM 的重要性，只要科学地制定变电站的建设和运行策略，预期可获得的成本降幅是相当可观的。

4 结语

本文针对地下变电站LCC 管理中存在许多不确定性因素的特点，将模糊理论引入LCC 的估算过程，提出了应用模糊平滑法估算LCC 分量的方法，并进一步将预测结果模糊化，最终以模糊集合的形式得到LCC 的估算结果。估算方法可操作性强，估算结果合理可信，具有很高的参考价值。

具体取得的创新性成果主要有：

（1）在分析地下变电站成本构成的基础上建立其LCC 的估算模型，并结合地下变电站特点，合理地设定了CI 和CF 等LCC 分量的特征影响因素。

（2）模糊平滑估算的过程中，通过不断地估算检验和对隶属度的优化调整，很大程度上避免了主观因素对估算结果的影响。

（3）模糊集合形式的估算结果明确了LCC 的估算区间和取值可信度，更加科学全面地反映了估算结论，同时体现了LCC 的不确定性。

当然，本文提出的LCC 估算方法还需要与地下变电站工程的实际招投标联系起来，以更好地指导评标管理，提高招投标的效用。同时，如何结合地下变电站的特点，用LCAM 的理念和方法指导变电站的运行和检修，实现真正的成本优化，也值得进一步的探索。

[1]王留萍（Wang Liuping）.大城市地下变电站设计中的若干问题研究（Research on Some Problems of Underground Substation Designing in Great City）[D].上海：上海交通大学电子信息与电气工程学院（Shanghai：School of Electronic Information and Electrical Engineering，Shanghai Jiao Tong University），2011.

[2]曹林放（Cao Linfang）.城市地下变电站的规划与设计（Planning and design of urban underground substations）[J].上海电力（Shanghai Electric Power），2002，（2）：8-11.

[3]秦杰（Qin Jie）.城市地下与地上变电站造价分析（Cost analysis between urban underground and ground substations）[J]. 上 海 电 力（Shanghai Electric Power），2005，（2）：155-157.

[4]徐翀（Xu Chong）.全寿命周期成本管理在电力设备管理中的应用探讨（Research of the application in power equipments′ LCC management）[J]. 中 国 电 力（Electric Power），2010，43（3）：72-74.

[5]Gaul A J，Schneider J，Neumann C，et al. Asset management techniques[J].International Journal of Electrical Power and Energy Systems，2006，28（9）：643-654.

[6]卜虎正，刘志斌，汪觉恒，等（Bu Huzheng，Liu Zhibin，Wang Jueheng，et al）.变电工程全寿命周期设计辅助决策系统的研发（Design and development of decision support system for substation project design based on life cycle cost theory）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2011，23（5）：94-98.

[7]张俊（Zhang Jun）.基于全寿命周期成本（LCC）的变电站建设的决策分析（Decision-Making Analyze of Electric Substation’s Construction Based on Life Cycle Costs）[D].重庆：重庆大学电气工程学院（Chongqing：College of Electrical Engineering，Chongqing University），2007.

[8]臧宝刚（Zang Baogang）.全寿命周期成本分析在变电站建设中的应用研究（Application Research on Life Cycle Cost Analysis in Power Substation Construction）[D]. 北京：华北电力大学经济与管理学院（Beijing：College of Economics and Management，North China Electrical Power University），2011.

[9]路石俊，李翔（Lu Shijun，Li Xiang）.基于盲数理论的变电站工程全寿命周期成本估算（Full life-cycle cost estimation of substation project based on blind number theory）[J]. 电网技术（Power System Technology），2010，34（3）：141-145.

[10]江修波，吴文宣，陈祥伟（Jiang Xiubo，Wu Wenxuan，Chen Xiangwei）.区间分析法在电力变压器全寿命周期成本模型中的应用（Transformer life cycle cost model based on interval analysis）[J].电力自动化设备（Electric Power Automation Equipment），2011，31（9）：50-53.

[11]张媛（Zhang Yuan）.基于灰色系统理论的电力设备全寿命周期成本评估及模型（Electric Power Equipment’s Life Cycle Cost Assessment and Model Based on Grey System Theory）[D]. 重 庆：重 庆 大 学 电 气 工 程 学 院（Chongqing：College of Electrical Engineering，Chongqing University），2008.

[12]吴添祖，冯勤，欧阳仲健.技术经济学[M].北京：清华大学出版社，2004.

[13]史秀建，金家善，吴奕亮（Shi Xiujian，Jin Jiashan，Wu Yiliang）. 寿命周期费用与可靠性关系模型分析研究（Analysis of life cycle cost and reliability relation model）[J].武汉理工大学学报：交通科学与工程版（Journal of Wuhan University of Technology：Transportation Science and Engineering），2004，28（4）：589-592.

[14]谢季坚.模糊数学方法及其应用[M].湖北：华中科技大学出版社，2006.

[15]黄伟，费维刚，王炳革，等（Huang Wei，Fei Weigang，Wang Bingge，et al）.模糊理论在中长期负荷预测中的应用（The application of fuzzy theory in the long and medium term load forecasting）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），1999，11（4）：25-29.

[16]梁丽莉，李立军（Liang Lili，Li Lijun）.工程合理成本的模糊预测技术研究（Research on fuzzy forecasting technology reasonable of project cost）[J].太原理工大学学报（Journal of Taiyuan University of Technology），2011，42（1）：88-91.

[17]国家电网公司.国家电网公司电网检修运维和运营管理成本标准[Z].北京：国家电网公司，2009.