二次曲线视角下含两个绝对值的不等式的解法

赵兴杰，张晓兰，王丽蓉

（1.遵义师范学院数学与计算科学学院，贵州遵义563002；2.遵义五中，贵州遵义563003；3.遵义市上海路学校，贵州遵义563002）

二次曲线视角下含两个绝对值的不等式的解法

赵兴杰1，张晓兰2，王丽蓉3

（1.遵义师范学院数学与计算科学学院，贵州遵义563002；2.遵义五中，贵州遵义563003；3.遵义市上海路学校，贵州遵义563002）

分别利用椭圆和双曲线的轨迹定义，总结出了|x-a|+|x-b|≥c（或≤c）和|x-a|-|x-b|≥c（或≤c）型不等式的简单解法，既克服了利用绝对值几何意义在三个区间上分别讨论或去绝对值分别讨论的烦琐，又避免了作分段函数图象的困难，还能利用“椭圆的焦距不大于直径（定长）的原理”，迅速求出不等式|x-a|+|x-b|≥c（或≤c）中待定参数的取值范围。

绝对值；不等式；公式；方法

|x-a|+|x-b|≥c（或≤c）和|x-a|-|x-b|≥c（或≤c）型不等式是近四年高考全国卷及大多数省（区、市）的命题内容之一，一般为5分。如2012年全国课标卷第24题（1）（5分）；2013年全国课标Ⅰ卷第24题（1）（5分）；2013年重庆卷第16题（5分）；2010年、2011年和2012陕西卷第15题（5分）；2011年山东卷第4题（5分）；2012年江西卷第15题（5分）；2012年广东卷第9题（5分）；2011年辽宁卷第24题（10分）；2011年天津卷第13题（5分）等。因此，该类型的不等式是选修4-5《不等式选讲》的教学重点之一。

对前两种类型的不等式，《普通高中数学课程标准（实验）》教科书选修4-5《不等式选讲》在17～19页介绍了三种解法：第一种方法是利用绝对值的几何意义，以分实数轴为三个区间后，分别在三个区间上讨论不等式的解的情况，最后综合得到不等式的解集；第二种方法是去绝对值分类讨论，最后综合得到不等式的解集；第三种方法是图象法，利用不等式构造分段函数，作出图形，根据图形求解。这三种方法虽然分别体现了“数形结合思想”、“分类思想”和“函数思想”，但就解法过程来看，均有弱点：前两种方法都需要讨论，最后综合得出解集，显得烦琐；第三种作图方法对于不少的学生来说，将绝对值函数表示为分段函数本身就是教学的难点。教科书配套的教师用书亦无新的方法介绍。虽然文[4]以两个例子分别介绍了“构造椭圆模型”和“构造双曲线模型”解不等式的思路，文[5]也介绍了“构造双曲线模型”解不等式，但两文均未较系统地给出解法。笔者分别利用椭圆和双曲线的轨迹定义，系统地总结出两类不等式的简单解法，利用其原理，可迅速求出不等式中待定参数的取值范围。这种方法，既克服了利用绝对值几何意义在三个区间上分别讨论或去绝对值分别讨论的烦琐，又避免了作分段函数图象的困难，可对高中数学教学提供参考。

1 |x-a|+|x-b|≥c（≤c）型不等式的解法

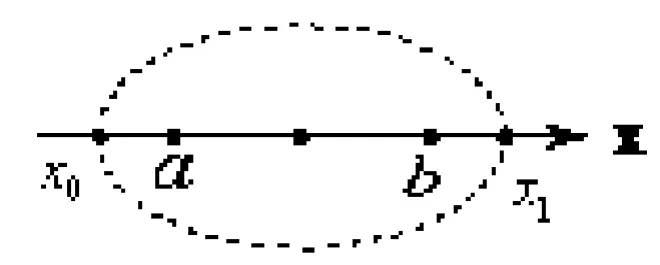
图1

不妨假设椭圆的长轴为x轴，两个焦点分别为（a,0）和(b,0)，且(a＜b)，定长（直径）为c，椭圆与长轴的交点的横坐标为x0与x1，则当y=0时，x0,x1恰好是x轴上到a和b的距离等于定长c的点（如图1），即x0,x1是|x-a|+|x-b|=c的两个根，因此，x轴上到（a,0）和(b,0)的距离大于定长c的点必定落在这两根之外，即不等式|x-a|+|x-b|≥c的解集为(-∞,x0]∪[x1,+∞)。同理，不等式|x-a|+|x-b|≤c的解集是［x0,x1］。从而，对于a＜b和c(≥0)，只要求出x0,x1，可得出不等式|x-a|+|x-b|≥c和(≤c)的解集，而根据图1可得

例1（2012年高考理科数学全国课标卷第24题）已知函数ƒ(x)=|x+a|+|x-2|，（1）当a=-3时，求不等式ƒ(x)≥3的解集。

解 因为不等式|x-3|+|x-2|≥3的解在方程|x-3|+|x-2|=3两根x0,x1之外，而所以，当a=-3时，不等式ƒ(x)≥3的解集为(-∞,1]∪[4,+∞)。

例2（教科书［2］20页8.(3)）解不等式|x-1|+|x-2|＜2。

解因为|x-1|+|x-2|＜2的解在方程|x-1|+|x-2|=2两根x0,x1之内，而所以，不等式的解集为

事实上，利用“椭圆的焦距不大于直径（定长）的原理”，还可以迅速求出不等式中待定参数的取值范围。

例3（2011年陕西卷第15题）若关于x的不等式|a|≥|x+1|+|x-2|存在实数解，则实数a的取值范围是______。

解因为不等式有实数解，所以，根据“椭圆的焦距不大于直径（定长）”得|2-(-1)|≤|a|，即a∈(-∞, 3]∪[3,+∞)。

例4（2012年陕西卷第15题）若存在实数x使|x-a|+|x-1|≤3成立，则实数a的取值范围是______。

解因为存在实数x使不等式成立，所以，根据“椭圆的焦距不大于（直径）定长”得|a-1|≤3，即a∈［-2,4］。

例5（2013年重庆卷第16题）若关于实数x的不等式|x-5|+|x+3|＜a无解，则实数a的取值范围是______。

解因为“椭圆的焦距不大于直径（定长）”，而不等式无解，所以a≤5-(-3)=8，，即实数a的取值范围是(-∞，8］。

2 |x-a|-|x-b|≥c（≤c）型不等式的解法

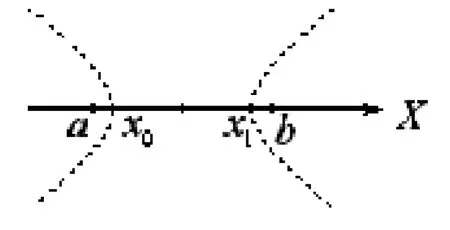
图2

因为，当|c|＜b-a时，平面上到两定点(a,0)和(b, 0)的距离之差等于定长|c|的点的轨迹，是以(a,0)和(b,0)为焦点，两顶点的距离为|c|的双曲线（如图2）。所以，当|c|=x1-x0＜b-a时，方程|x-a|-|x-b|=|c|的根是双曲线的右半支与x轴的交点的横坐标x1，于是|xa|-|x-b|≥|c|的解集为[x1，+∞)，|x-a|-|x-b|≤|c|的解集为(-∞，x1］。由于于是因此，当c＞0时，|x-a|-|x-b|≥c的解集为的解集为

同理，由于双曲线的左半支与x轴的交点的横坐标x0，而于是，当c＜0时，|x-a|-|x-b|≥c的解集为≤c的解集为取c=0，便得到|x-a|-|x-b|≥0的解集为的解集为

例6（2010年陕西卷第15题）不等式|x+3|-|x-2|≥3的解集为______。

例7（2012年广东卷第9题）|x+2|-|x|≤1的解集为______。

例8（2012年湖南卷第10题）不等式|2x+1| -2|x-1|＞0的解集为______。

解 不等式|2x+1|-2|x-1|＞0等价于|x+

3 结束语

本文仅对含两个绝对值，且其中x的系数相同的不等式的解法进行了总结。对于两个绝对值中的系数不同的不等式的解法，还有待进一步研究。

[1]中华人民共和国教育部.普通高中数学课程标准（实验）[M].北京：人民教育出版社,2003.

[2]人民教育出版社,课程教材研究所，中学数学课程教材研究开发中心.普通高中课程标准实验教科书数学选修4-5（A版）不等式选讲（第2版）[M].北京：人民教育出版社,2007.

[3]人民教育出版社,课程教材研究所，中学数学课程教材研究开发中心.普通高中课程标准实验教科书数学选修4-5（A版）不等式选讲教师用书（第2版）[M].北京：人民教育出版社,2007.

[4]冯作维,张国彬.构造圆锥曲线模型巧解不等式[J].中学教学参考(理科版),2013,(3)：50.

[5]刘冰.构造圆锥曲线模型巧解题[J].高中生学习(高二版), 2012,(3)：32.

（责任编辑：朱彬）

Method of Solving Two Absolute Inequation under the Perspective of Quadratic Curve

ZHAO Xing-jie1,ZHANG Xiao-lan2,WANG Li-rong3
(1.School of Mathematics and Computational Science,Zunyi Normal College,Zunyi 563002,China;2.NO.5 Middle School of Zunyi, Zunyi 563002,China;3.Shanghai Road School of Zunyi,Zunyi 563002,China;)

In this paper,the authors use track definition of ellipse and hyperbola to conclude a simple solution of the inequation|x-a|+|x-b|≥c（≤c）and|x-a|-|x-b|≥c（≤c）,where the trivialdiscussiondetails with or without the geometric mean of theabsolute value in three intervals are overcome,and the difficulties drawing a piecewise function image are avoided,and the principle in which the ellipse focal length is less than or equal to diameter(fixed length)is also adopted to quickly determine undetermined parameters scope in|x-a|+|x-b|≥c（≤c）.

absolute value;inequation;formula;method

G632.0

：A

1009-3583（2014）-0109-02

2014-04-25

遵义师范学院基础教育研究课题（13ZYJ031）

赵兴杰，男，贵州习水县人，遵义师范学院数学与计算科学学院教授，主要从事数学教学研究。