四次C-Bézier曲线的形状修改

秦新强，申晓利，胡钢

西安理工大学理学院，西安710054

1 引言

曲线曲面的形状修改一直是CAGD领域中一项基本的技术，对于曲线的实用化有着重要的意义，许多学者在这一领域已做了大量的研究工作[1-4]。C-Bézier曲线曲面[4-8]作为CAGD中一种新颖的造型曲线曲面，不仅保留了传统Bézier曲线曲面的许多优点，而且能够方便、精确地构造常规的二次曲线曲面，还具有算法简单，存储空间小，参数选择容易等特点，因此其在描述曲线曲面方面有着重要的作用。本文在分析四次C-Bézier曲线几何模型[9]的基础上，对四次C-Bézier曲线的形状调整进行了研究，通过修改曲线的控制顶点和形状参数，分别提出了两种调整四次C-Bézier曲线形状的有效新方法，并给出了具体的实例。

2 四次C-Bézier曲线的定义及性质

定义1 对任意的t∈[0，α]，α∈[0，2π]，称为空间Φ=span{sin t，cos t，t2，t，1}上的一组正规B基[9]，式中u4(t)=t2-2 cos C(t)，S=sin C(α)=α-sinα，C=cos C(α)=1-cosα，cos C(t)=1-cos t，Z3(t)=sin C(t)/S。

定义2 设Pi(i=0，1，2，3，4)为曲线的控制顶点向量，α是任意实数，且0≤t≤α，0≤α≤2π，则曲线

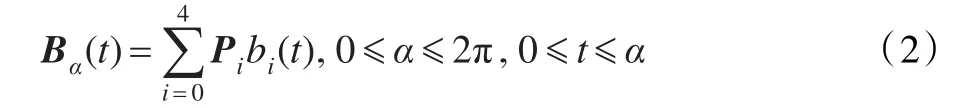
称为四次C-Bézier曲线[9]。其中bi(t)  (i=0，1，2，3，4)为式所定义的基函数。当α→0时，四次C-Bézier曲线逼近于四次Bézier曲线。由式（1）和（2）可以推出四次C-Bézier曲线具有凸包性、变差缩减性、保凸性，以及如下的端点性质。

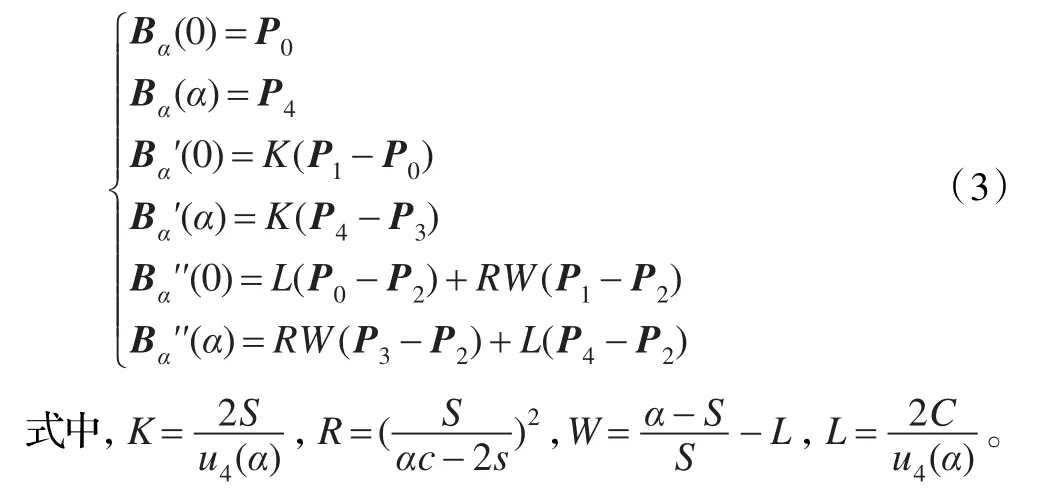
由于形状控制参数α的引入，使得四次C-Bézier曲线具有比传统Bézier曲线更强的曲线表达能力。当曲线的控制顶点固定不变时，让α在(0，2π)之间变化可产生一族四次C-Bézier曲线。图1给出了一族α取不同值的四次C-Bézier曲线图形，图中曲线从上到下对应的参数依次取值为α=2，π，6，2π。

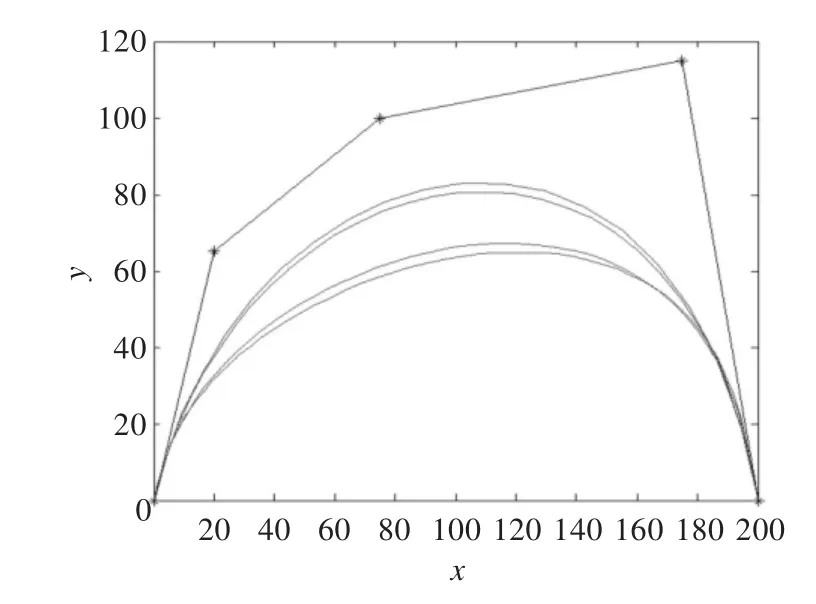
图1 一族α取不同值的四次C-Bézier曲线

3 基于自身参数的四次C-Bézier曲线的形状修改

四次C-Bézier曲线是由基函数和控制顶点混合生成的，由于其基函数中引入了的形状控制参数α，所以增强了四次C-Bézier曲线的形状控制能力。显然，形状参数α和控制顶点都会影响着曲线的整体形状。

3.1 调节控制参数α修改曲线的形状

假设控制顶点的位置保持不变，对于τ∈[0，1]，m，n分别为xlim(0，τ)和x(2π，τ)上的点，则可近似地认为α轨道上的点s(α，τ)在mn的连线上，且有

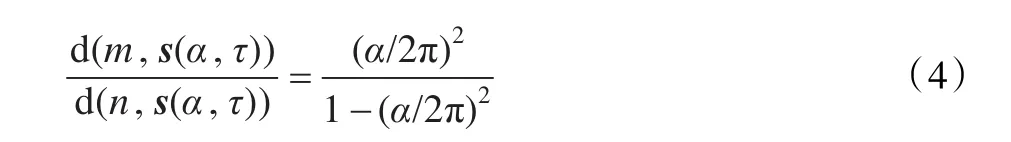
这一近似方法即可以将参数α对曲线的作用用直观的形式表达出来，又可以为通过调节控制参数α来修改曲线的形状提供了依据。

当α减小时，四次C-Bézier曲线逐渐靠近相应的四次代数多项式曲线xlim(0，τ)；当α增加时，四次C-Bézier曲线逐渐靠向相应的α=2π时的C曲线x(2π，τ)，(0＜τ≤1)。所以，参数α对整条曲线段的调节范围便是xlim(0，τ)和x(2π，τ)之间的区域。

在实际的工程曲线设计中，经常需要求一条曲线经过某给定的点。设S为调节范围内的任一点，根据上面对α作用的分析，只要S位于xlim(0，τ)和x(2π，τ)之间的区域，就可以通过选择合适的α使得四次C-Bézier曲线通过点S。

以下可分两步完成，具体做法如下：

（1）求τ。可采用二分法通过逐步求精反求τ。xlim(0，τ)和x(2π，τ)之间的直线段表示如下：

P1(k，τ)=kx(2π，τ)+(1-k)xlim(0，τ)，0≤k≤1

显然希望找到τ0使得S在P1(k，τ0)上，具体算法为：

步骤1 取初值a=0，b=1；

步骤2 令τ0

步骤3 若S在P1(k，τ0)上，输出τ0，否则转步骤4；

步骤4 若S在P1(k，τ0)的左侧，则令b=τ0，若S在P1(k，τ0)的右侧，则a=τ0，转步骤2。

通过此算法便可以求出τ0使得s(a，τ0)过已知点S。

（2）求α。由第（1）步求出的τ0可计算d1=d(S，x(2π，τ0))和d2=d(S，xlim(0，τ0))，因此由式（4）可得：

如果此时得到的α不满足精度要求，还可以利用二分法，进一步提高精度直至满足要求。具体步骤为：

步骤1 将α和τ0带入四次C-Bézier曲线的方程得到点S′；

步骤2 若S′与S的近似精度满足要求，则输出S′，否则步骤3；

步骤3 若S′比S的更靠近xlim(0，τ)，则令反之令a=，转步骤1。

3.2 调节控制顶点修改四次C-Bézier曲线的形状

假设S为式（2）所定义的一条四次C-Bézier曲线Bα(t)上的某一点，其对应的变量t值为ts，要使S点移动到给定的T点，可通过调整控制顶点的位置来实现。不妨假设曲线各控制顶点Pi的位移矢量分别为δi(i=0，1，2，3，4)，则曲线上每点的位移量可表示为：

式中，0≤t≤1。

实际工程应用中常使用以下两种方法：

（1）保持首末两点的位置不变，采用约束优化方法使整条曲线的变形最小。

首先，建立如下约束条件：

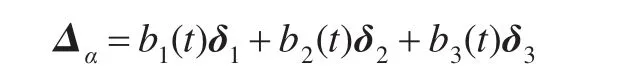
其目标函数为：

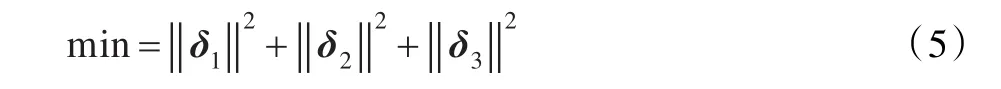
其次，为了使得上述目标函数取最小，由拉格朗日乘数法可以定义拉格朗日方程为：

式中，λ=[λx，λy，λz]为拉格朗日乘数向量。令

则可得如下方程组：

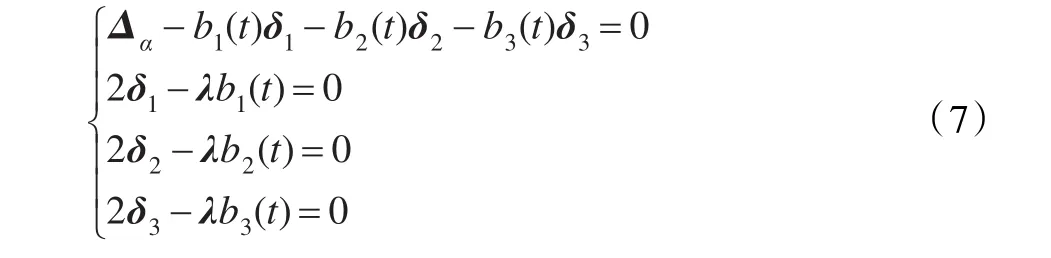
最后，解上述方程组式（7），便可求得中间3个控制顶点的位移为：

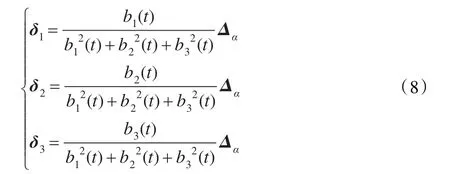
由此可见，采用约束优化的方法移动中间3个控制顶点，控制顶点的位移方向与曲线上给定点的移动方向相同，其大小与相应的四次C-Bézier基函数成正比。

（2）保持首末点的位置和切矢方向不变。为了保证四次C-Bézier曲线段之间的G1连续，每段曲线在形状修改时，首末点的位置和切矢方向都应保持不变，再使中间点P2位置不变，另外两点P1、P3的位移δ1、δ2满足：

式中，前两个条件保证了调整控制顶点前后曲线的首末点的切矢方向不变。

上述方程组的几何意义是将Δα在两个方向(P1-P0)和(P4-P3)上分解成Δα1和Δα2，那么

式中，δ1、δ2分别为P1、P3的位移矢量。

图2给出了一个通过移动曲线控制顶点来修改四次C-Bézier曲线形状的实例。图2中，曲线的形状参数α=2π，而图2（a）、图2（b）和图2（c）中分别移动的控制顶点个数分别为5个、3个和2个。

图3给出了在保持端点性质条件下的四次C-Bézier曲线形状修改的实例。图3（a）保持了首末端点位置不变，而图3（b）保持了首末点位置和切矢都不变。

图2 移动控制顶点改变四次C-Bézier曲线形状几何造型

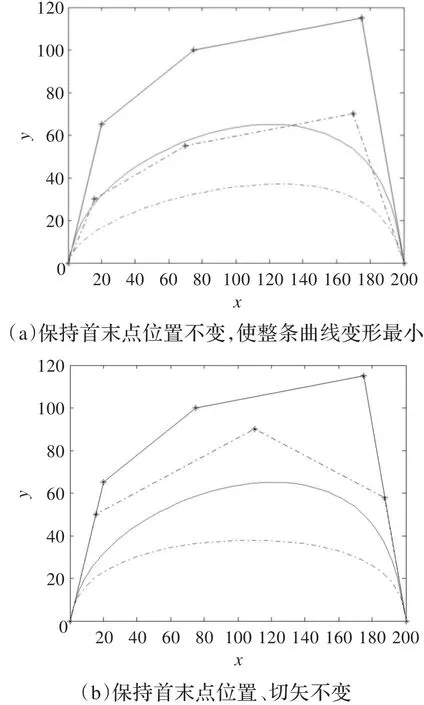
图3 调节控制顶点来修改四次C-Bézier曲线的形状

4 结论

基于四次C-Bézier曲线的几何模型，分别通过修改曲线的控制顶点和形状参数，提出了两种调整四次C-Bézier曲线形状的有效新方法。本文方法不仅增加了四次C-Bézier曲线造型方法的灵活性，在一定程度上克服了工程中该曲线形状难以调节和控制的问题，而且还可以达到使曲线经过给定目标点或满足一定条件的近似表示的目的，在CAD/CAM工程中的应用也较为广泛。

[1]Mainar E，Pena J M，Sánchez-Reyes J.Shape preserving alternatives to the rational Bézier model[J].Computer Aided Geometric Design，2001，18：37-60.

[2]宋丽平，秦新强，祁伟丽.C-B样条曲线的形状修改[J].计算机技术与发展，2008，18（7）：122-125.

[3]杭颖.C曲线及其形状修改[D].合肥：合肥工业大学，2009.

[4]樊建华，张纪文，邬义杰.C-Bézier曲线的形状修改[J].软件学报，2002，13（11）：2194-2199.

[5]Zhang Jiwen.C-Curves：an extension of cubic curves[J].Computer Aided Geometric Design，1996，13（3）：199-217.

[6]Zhang Jiwen.C-Bézier curves and surfaces[J].Graphical Models and Image Processing，1999，61（1）：2-15.

[7]Hoffmann M，Wang Guozhao.Paths of C-Bézier and C-B-splines curves[J].Computer Aided Geometric Design，2006，23：463-475.

[8]陈秦玉，汪国昭.圆弧的C-Bézier曲线表示[J].软件学报，2002，13（11）：2154-2161.

[9]陈秦玉，杨勋年，汪国昭.四次C-曲线的性质及其应用[J].高校应用数学学报：A辑，2003，18（1）：45-50.