基于ARM A-RESN的网络流量预测

王雪松，赵跃龙

1.佛山职业技术学院电子信息系，广东佛山528137

2.华南理工大学计算机科学与工程学院，广州510640

1 引言

近年来，互联网始终处于一种高速发展的态势，相对于10年前网络，目前网络覆盖面更广，用户数量更庞大，应用范围更宽，这些变化给人们带来了方便的同时，也给网络管理带来巨大挑战[1]。网络流量预测可以发现网络流量异常，有利于更好地管理网络，受到网络研究工作者关注[2]。

传统网络流量预测方法主要有自回归法（AR）、自回归移动平均（ARMA）等线性预测技术，尤其是ARMA模型融合了回归分析和时间序列分析功能，在网络流量预测中取得了不错效果[3-4]。随着网络流量研究的不断深入，研究者们发现网络流量不仅具有线性变化特性，同时具有随机、混沌性和突变性等非线性变化特性，而传统方法无法描述网络流量的非线性变化特性，应用范围受限[5]。随着非线性理论发展，出现了基于神经网络、支持向量机、相关向量机等网络流量预测模型，并且获得了较理想的预测效果[6-9]。传统神经网络在训练样本数量大的条件下，才可以获得较高的网络流量预测精度，当训练样本有限时，预测结果存在过拟合现象；支持向量机、相关向量机虽然泛化能力优异，但是存在训练耗时长，效率低，不能满足网络流量在线的要求[10-11]。正则化回声状态网络模型（Regularized Echo State Network，RESN）是一种新型的神经网络，不仅克服了传统神经网络过拟合的缺陷，同时解决了支持向量机等训练效率低的缺陷，在网络流量预测中得了广泛的应用[12]。但是大量研究表明，RESN虽然可以获得较好的非线性网络流量预测结果，但是实际网络流量受到多种因素综合影响，不仅存在非线性变化特性，同时存在线性变化特性，这样RESN难以对线性变化特性准确刻画。因此对于复杂多变的网络流量，单一的RESN或ARMA均难以建立准确的预测模型，预测精度有待进一步提高。

针对ARMA和RESN存在的不足，为了获得更加理想的网络流量预测结果，提出一种基于ARMA-RESN的网络流量预测模型（ARMA-RESN）。首先利用ARMA强大的线性拟合能力，对网络流量进行建模，得到线性变化预测结果，然后采用非线性捕捉能力优异的RESN对网络流量非线性变化特性进行预测，对两者预测值进行融合得到网络流量的最终预测结果，并采用具体网络流量数据进行仿真实验，以验证ARMA-RESN的可行性和优越性。

2 ARM A和RESN

2.1 ARM A

ARMA是一种线性预测能力优异的时间序列模型，其由AR和移动平均（MA）两部分组成，描述当前时刻预测值同时与以前时刻自身值和误差扰动直接相关。当AR=0时，ARMA模型变化为MA(q)模型，MA=0时，ARMA模型变为AR(p)模型[13]。AR(p)模型为：

式中，ε(t)表示误差；v和φi(i=1，2，…，p)为待估计的参数。

如果ε(t)自相关，那么MA(q)模型可以表示为：

式中，Θj(j=1，2，…，q)为待估计的参数；a(t)是零均值白噪声。

综合上述可知，ARMA(p，q)模型为：

如果阶数n比较大，那么AR(n)模型可以近似等价为ARMA(p，q)，则有：

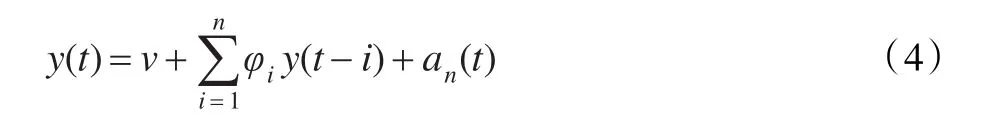
式中，an(t)表示阶数为n时的误差项。

根据式（5）可以得到an(t)的估计值：

根据式ân(t)可以建立ARMA(p，q)模型：

通过采用AIC准则确定ARMA模型的参数n、p和q，即：

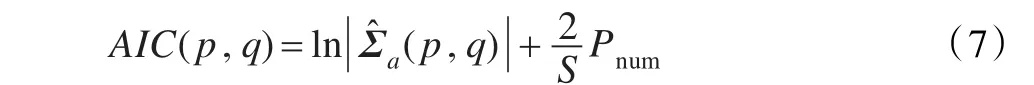
2.2 RESN模型

RESN是一种由输入层、内部储备池和输出层组成的非线性递归神经网络，储备池起到存储历史信息的作用，是RESN的核心部分，保证了网络的回声性质。RESN状态方程为：

式中，sigmoid为激活函数；Win和Wx分别为输入和储备池内部的连接矩阵；u(t)、x(t)分别表示t时刻的输入向量和储备池内部状态向量。

那么RESN的输出方程为：

式中，y(t)为t时刻的输出向量；Wout为输出连接向量，是惟一需要通过训练进行求解的参数。

输出权值对RESN性能起着关键作用，常采用最小二乘法进行求解，目标函数的最小化形式为：

式中，X=[x(1)，x(2)，…，x(l)]T，Y=[y(1)，y(2)，…，y(l)]T，X∈Rl×N，N为储备池节点数；l为训练样本数。

对于大规模网络流量数据，训练样本数常大于储备池节点数，那么，根据式（10）得到解：

设状态矩阵X的奇异值分解为：

式中，U=(u1，u2，…，ul)和V=(v1，v2，…，vl)是酉阵，对角矩阵Σ=diag(σ1，…，σr，σr+1，…，σN)。

如果X的秩为r，那么奇异值为：

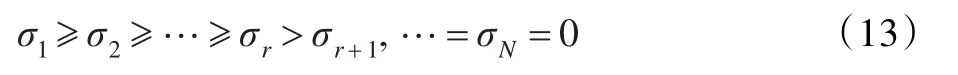
X+可以描述为：

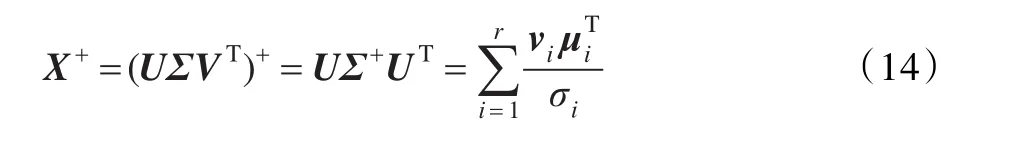
有

对于实际采集的网络流量数据常含有扰动信号ep，则目标值变为=Y+ep，输出权值计算公式变为：

根据式（16）可知，奇异值大小与输出权值幅值是一种反比例关系，如果奇异值过小，那么RESN模型就会得到病态解，ep对过大，网络泛化性能就越差。为解决该难题，在目标函数中增加正则项，并将岭回归方法应用于RESN模型的储备池网络中，以提高泛化能力，那么有：值产生不利影响。

式中，u∈R+表示正则项系数。

其与最小化代价函数等价：

由于施加正则项，防止σi过小现象的发生，使输出权值幅值减小，对模型误差项和复杂度进行较好的平衡，使RESN模型具有更优的泛化能力。

3 ARM A-RESN混合预测模型

RESN可以对非线性函数输入、输出映射的关系进行较好拟合，然而网络流量受到多种因素影响，实际收集的网络流量数据一般包括非线性和线性特性，因此RESN对于网络流量的线性性能不能较好刻画，难以得到满意的网络流量预测效果。鉴于以上分析，提出一种ARMA-RESN的网络流量预测模型（ARMA-RESN），采用ARMA和RESN分别对网络流量线性和非线性特性进行建模与预测，以刻画网络流量的动力学变化特性，以提高预测精度。ARMA-RESN的网络流量预测模型工作流程如图1所示。

图1 网络流量的工作流程图

4 仿真实验

4.1 数据来源

为验证ARMA-RESN网络流量预测模型的有效性，数据源于标准流量文库：http：//netnew s.nctu.edu.tw/～new s/innreport/的每小时网络访问流量作为仿真对象，共获得3 000个数据，具体如图2所示。选择前2 500个数据作为训练集，建立网络流量预测模型，其余500个样本作为测试集对模型性能进行检验。

图2 标准文库的网络流量数据

同时为了测试ARMA-RESN的鲁棒性，采用含有噪声的网络流量进行对比仿真实验，具体如图3所示，其中前800个数据作为训练集，其余200个数据作为测试。所有仿真实验环境均为W indow s XP操作系统，Intel®CoreTMi3-2120 2.8 GHz CPU，4 GB RAM，采用VC++编程实现。

图3 含噪的网络流量数据

4.2 结果与分析

ARMA对图2的网络流量的预测结果及预测误差如图4和5所示，对含噪的网络流量的预测结果及预测误差如图6和7所示。从图4～7可知，ARMA可以较好地对网络流量的线性变化规律进行描述，但是预测结果误差比较大，尤其对于含噪网络流量数据，预测误差大幅度增加，预测结果极不稳定。这表明ARMA不能对非线性、随机变化特点进行准确描述，难以建立预测精度高的网络流量预测模型，应用范围受限。

图4 ARMA的标准网络流量预测结果

图5 ARMA的标准网络流量预测误差

图6 RESN的含噪网络流量预测结果

图7 RESN的含噪网络流量预测误差

图8 标准网络流量的延迟时间计算

图9 标准网络流量的嵌入维数计算

图10 含噪网络流量的延迟时间计算

图11 含噪网络流量的嵌入维数计算

计算网络流量真实值与ARMA的预测结果之间的误差，得到残差序列，然后采用相关系数法和关联维法分别确定残差序列的延迟时间和嵌入维数，分别如图8～图11所示。从图8～图11可知，对于标准网络流量数据，最优延迟时间τ=3，m=5。对于含噪网络流量数据，最优延迟时间τ=6，m=3。

采用τ=3，m=5对标准网络流量数据进行重构，τ=6，m=3对含噪网络流量数据进行重构，建立相应的RESN网络流量预测模型，它们的预测结果分别如图12和图13所示。从图12和图13可知，RESN模型可以对网络流量的非线性变化特征进行准确刻画，预测十分理想。然后将ARMA和RESN的预测结果进行融合，得到网络流量的最终预测结果，分别如图14和15所示。从图14和15可知，ARMA-RESN的预测精度相当的高，网络流量的实际值和预测值吻合得相当的好，预测误差相当小，预测误差变化比较平稳，网络流量预测结果十分可靠。

图12 RESN的标准网络流量残差预测结果

图13 RESN的含噪网络流量残差预测结果

图14 ARMA-RESN的标准网络流量预测结果

图15 ARMA-RESN的含噪网络流量预测结果

4.3 与其他网络流量模型的性能对比

为了使ARMA-RESN的网络流量预测结果具有可比性，选择ARMA、RESN、支持向量机（RVM）、RBF神经网络（RBFNN）、文献[14]的改进RESN模型（SVESM）和文献[15]的改进RESN模型（ESGP）进行对比实验。采用均方根误差（RMSE）和平均绝对百分率误差（MAPE）作为预测性能的评价指标，它们计算公式为：

对于网络流量测试集，不同模型的预测误差见表1。对表1的各模型误差进行分析可以得到如下结论：

（1）单一ARMA模型和RESN模型的网络流量预测误差比较大，主要由于网络流量受到多种因素综合影响，具有时变性、非线性、自相似性等变化特点，单一线性或非线性模型难以建立预测精度高的网络流量预测模型，应用范围受限。

（2）相对于ARMA模型，改进RESN模型（ESGP、SVESM）获得较高的预测精度，这主要是由于改进RESN模型具有更强的非线性建模能力，因此获得比较理想的网络流量预测结果。

（3）相对于SVM、RBFNN，ARMA-RESN的预测误差更小，预测精度更高，这表明ARMA-RESN较好地克服了SVM、RBFNN的不足，预测结果更优。

（4）ARMA-RESN预测值与网络流量真实值偏差最小，预测精度最高，明显好于其他模型。主要因为实际收集的网络流量数据含有较大随机误差，ARMA-RESN模型对误差进行了补偿，使预测值与网络流量真实值之间的偏差减少，更好地描绘了网络流量变化特性。

表1 不同模型网络流量预测误差比较

5 结束语

网络流量受到多种因素的影响，具有混沌性、非线性和时变性等变化特点，是一个复杂的动力变化系统，传统模型或单一模型存在预测精度低的缺陷，为了提高网络流量预测精度，提出一种基于ARMA-RESN的网络流量预测模型。首先分别采用自回归移动平均和回声状态网络对网络流量线性变化特征和非线性变化特性进行建模与预测，然后对自回归移动平均和回声状态网络的预测结果进行融合，得到网络流量最终预测结果，最后采用多个网络流量数据以及多个对比模型进行了仿真对比实验。仿真结果表明，相对于其他网络流量预测模型，ARMA-RESN不仅提高了网络流量的预测精度，而且具有更好的鲁棒性。

[1]王升辉，裘正定.结合多重分形的网络流量非线性预测[J].通信学报，2007，28（2）：45-57.

[2]王兆霞，孙雨耕，陈增强，等.基于模糊神经网络的网络业务流量预测研究[J].通信学报，2005，26（3）：136-140.

[3]Yu G Q，Zhang C S.Switching ARIMA model based forecasting for traffic flow[C]//Proceedings of ICASSP，2004，2：429-432.

[4]姜明，吴春明，胡大民.网络流量预测中的时间序列模型比较研究[J].电子学报，2009，37（11）：2353-2359.

[5]党小超，郝占军.季节周期性Elman网络的网络流量分析与应用[J].计算机工程与应用，2010，46（28）：98-101.

[6]孟庆芳，陈月辉，冯志全，等.基于局域相关向量机回归模型的小尺度网络流量的非线性预测[J].物理学报，2013，62（13）：1-7.

[7]Wang J S，Gao Z W.Network traffic modeling and prediction based on RBF neural network[J].Computer Engineering and Applications，2008，44（13）：6-11.

[8]黄悦.改进型Elman网络用于网络流量预测[J].计算机工程与应用，2010，46（24）：121-123.

[9]傅秀文，郑明春.基于改进的BP神经网络的Overlay网络流量预测[J].计算机工程与应用，2012，48（12）：83-87.

[10]冯华丽，刘渊，陈冬.QPSO算法优化BP网络的网络流量预测[J].计算机工程与应用，2012，48（3）：102-104.

[11]党小超，郝占军.基于改进Elman神经网络的网络流量预测[J].计算机应用，2010，30（10）：2648-2652.

[12]宋彤，李菡.小波回声状态网络的混沌时间序列预测[J].物理学报，2012，61（8）：1-7.

[13]许培，陈其工，葛愿，等.基于ARMA模型的NCS前向时延预测研究[J].计算机工程与应用，2013，49（20）：91-95.

[14]彭宇，王建民，彭喜元.基于回声状态网络的时间序列预测方法研究[J].电子学报，2010，21（8）：1609-1617.

[15]王建民，彭宇，彭喜元，等.基于扩展卡尔曼滤波的回声状态网络在线训练算法[J].仪器仪表学报，2011，32（7）：1514-1520.