基于改进随机移动算子的人工鱼群算法
淦艳,魏延,,杨有,万辉
1.重庆师范大学计算机与信息科学学院,重庆401331
2.重庆师范大学科研处,重庆401331
1 引言
生活中许多实际工程问题都可以归结为一个优化问题,为了寻找该优化问题的最优解,李晓磊等人于2002年提出一种自下而上的新型寻优方法——人工鱼群算法(Artificial Fish Swarm Algorithm,AFSA)[1-2]。在文献[1-2]中李晓磊等给出了人工鱼群觅食行为、聚群行为、追尾行为和随机行为的描述和具体实现。其算法的主要特点是通过比较和移动来实现寻优,易于实现和理解。
但是,使用人工鱼群算法在求解多峰函数优化(Multi-peaks Function Optimization)[3]时,存在求解精度有限,运行时间较长,算法易陷入局部最优,鲁棒性较差,以及收敛速率较慢和搜索效率不理想的缺点,有许多学者提出了改进算法。其中,针对计算精度不高的缺点,文献[4]引入模拟退火算法改进人工鱼群算法(Simulated Annealing AFSA,SA-AFSA);文献[5]采用特殊觅食行为和约束拥挤度区间的方法改进人工鱼群算法,文献[6]采用混合人工鱼群算法提高求解精度;文献[7]引入混沌搜索的思想改进人工鱼群算法,均取得了一定的成果。在综合考虑计算精度和收敛速率问题方面,文献[8]融合进化策略和粒子群算法改进人工鱼群算法;文献[9]也利用粒子群算法改进人工鱼群算法;文献[10]引入多父体杂交进化技术;文献[11]提出基于高斯变异算子与差分进化变异算子相结合的混合变异算子的人工鱼群算法;文献[12]针对0/1背包问题,采用随机键的方法以及单位价值启发式信息进行编码,直接在编码空间上进行求解,均提高了计算精度和收敛速率。在综合考虑计算精度、收敛速率和算法稳定性问题方面,文献[13]采用保留最优个体,根据双射的定义和性质,对问题的搜索域进行缩小,加速全局搜索;文献[14]利用优先适合启发算法去计算适应度函数值,从实验结果来看,比AFSA算法有所改进;文献[15]比较全面地总结了人工鱼群算法的改进算法,以及应用领域,并且指出算法存在时间复杂性高,缺乏平衡全局最优和局部最优的缺点。
目前,很少有研究综合考虑计算精度、鲁棒性以及收敛速率和搜索效率问题,只是考虑了其中的部分问题。基于此,本文受到文献[1-4,8-9,14-16]的启发,综合考虑AFSA算法计算精度、鲁棒性以及收敛速率和搜索效率问题,提出基于粒子群算法的人工鱼群算法(Particle Swarm Optimization AFSA,PSO-AFSA)和包含自适应扰动项的改进人工鱼群算法(Adaptive Disturbance Improved AFSA,ADI-AFSA)。对于PSO-AFSA算法主要是利用粒子群算法[3,8-9,16]改进聚群和追尾行为中的随机移动算子,以概率e-r改进觅食行为[4]中随机移动算子;对于ADI-AFSA算法主要是对觅食、聚群和追尾行为中随机移动算子进行改进,添加一项扰动,让它跳出局部最优值,从而进一步搜索到全局最优值;并从理论上证明了PSO-AFSA和ADI-AFSA算法的收敛性。通过实验仿真,验证了本文算法的有效性,避免在寻优时陷入局部最优,提高了AFSA在求解多峰函数最优值时的计算精度,同时验证了所提出算法比人工鱼群算法具有更好的鲁棒性,加快了收敛速率和提高了搜索效率。
2 人工鱼群基本算法
人工鱼群算法(AFSA)是一种新的群智能算法,主要是通过模仿鱼的觅食、聚群、追尾和随机行为来实现寻优的目的。为了更方便描述人工鱼群算法,假设:N表表示人工鱼个体i、j之间的距离;try_number表示觅食行为试探的最大次数;max gen表示最大迭代次数,gen表示当前迭代次数。如没有特殊说明,此假设适用于整篇文章。AFSA算法主要包括:觅食、聚群、追尾和随机行为,其基本思想如下描述。
觅食行为(AF-prey)[1-2,15,17-18]:设人工鱼i当前状态为Xi,在其感知范围内随机选择一个状态Xj,如果Yi<Yj(认为后者比前者更优),则向该方向前进一步示人工鱼群个体数目;Xi表示人工鱼个体的状态位置,用向量Xi=(x1,x2,…,xn)表示,其中xi(i=1,2,…,n)是寻优的变量;Yi表示第i条人工鱼当前所在位置的食物浓度,用Yi=f(Xi)表示目标函数;Visual表示人工鱼的感知距离;Step表示人工鱼移动的步长;δ表示拥挤度因子;,反之,再重新随机选择状态Xj,判断是否满足前进条件,并反复尝试try_number次,若仍不满足前进条件,则随机移动一步
聚群行为(AF-swarm)[1-2,15,17-18]:设人工鱼i当前状态为Xi,探索当前邻域内(di,j<Visual)的伙伴数目nf及中心位置Xc。若Yc/nf>δYi,表明伙伴中心有较多食物且不太拥挤,则朝伙伴的中心位置方向前进一步,否则执行觅食行为。
追尾行为(AF-follow)[1-2,15,17-18]:是一种向邻近的有着最高适应度的人工鱼追逐的行为,在寻优算法中可以理解为是向附近的最优伙伴前进的过程。设人工鱼i当前状态为Xi,探索当前邻域内(di,j<Visual)的伙伴中Yj为最大值的伙伴Xj,若Yj/nf>δYi,表明伙伴Xj的状态具有较高的食物浓度并且其周围不太拥挤,则朝Xj的方向前进一步,否则执行觅食行为。
随机行为(AF-move)[1-2,15,17-18]:随机行为就是在视野中随机选择一个状态,然后向该方向移动,其实是觅食行为的一个缺省值。
从AFSA算法的行为描述可知,在觅食行为、聚群行为和追尾行为中均出现随机移动的情况,会降低算法的收敛速率。针对收敛速率不乐观的问题,文献[18]提出了对觅食行为、聚群行为和追尾行为进行改进的策略,主要是限制随机移动的范围于定义区间内,让它在事先定义的区间内移动,这样可以加快收敛速率。实验仿真表明,可以提高计算的精度。为了后面表述方便,称其为限制随机移动的人工鱼群算法(Limited Move AFSA,LM-AFSA)。为了便于说明将文献[4]中SA-AFSA和文献[18]中LM-AFSA算法视为传统改进算法。
3 基于粒子群算法的人工鱼群算法
针对人工鱼群算法优化精度不足、鲁棒性较差,以及收敛速率较慢和搜索效率较低的缺点,受文献[3,8-9,16]的启发,本文提出了基于粒子群算法的人工鱼群算法(PSO-AFSA)。
3.1 PSO-AFSA算法思想
PSO-AFSA算法主要思想是利用粒子群算法改进聚群和追尾行为中的随机移动算子,改进的聚群行为随机移动算子描述如下:
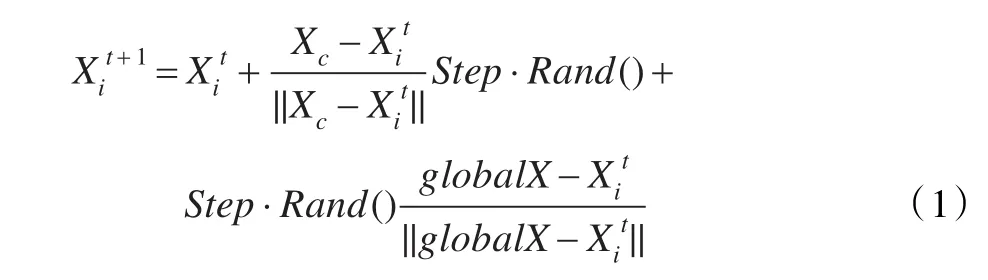
其中,Xc是中心位置,Rand()是0到1之间的随机数,globalX是全局的最优值,下同。改进的追尾行为随机移动算子描述如下:
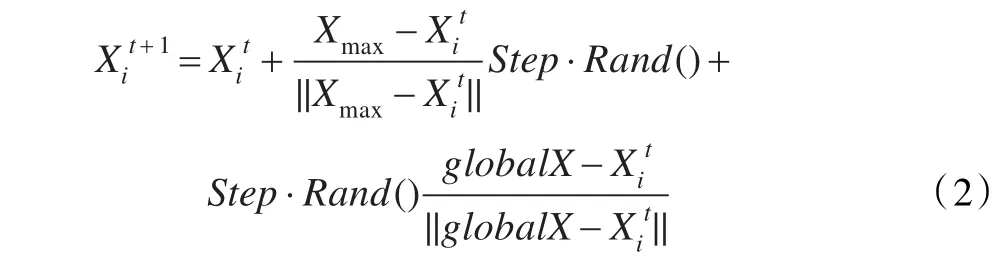
其中,Xmax是探索其视野范围内最优的一个值。其次,就是以概率e-r改进觅食行为[4]中随机移动算子,其中r=i/max gen,即满足概率e-r,就执行觅食行为的随机移动算子,其描述如下:

如果不满足概率e-r,则直接移动到Xj,即并且限制觅食、聚群和追尾行为中向前移动一步的范围,具体做法是:当时,取;当时,取=Xmin;这样就在定义区间[Xmin,Xmax]内。另外采用公告牌用来记录最优人工鱼个体状态,每条人工鱼在每次寻优过程完成后,自动与公告牌的状态相比,如果自身状态优于公告牌状态,就将公告牌状态替换为自身状态,这样公告牌就记录了最优的人工鱼状态。
3.2 PSO-AFSA算法描述
首先初始化参数,然后执行聚群行为、觅食行为、追尾行为和随机行为,采用公告牌记录最优值,详细的描述见算法1。
算法1基于粒子群算法的人工鱼群算法(PSO-AFSA算法)
步骤1初始化人工鱼群中参数和公告牌信息,即:N、Visual、try_number、δ、max gen、gen=1、BestY、BestX;公告牌中参数:besty、bestx。
步骤2 执行聚群行为、觅食行为、追尾行为和随机行为,具体在执行聚群、追尾和觅食行为中的随机移动算子时,分别按照式(1)、(2)和(3)所给的移动算子执行。
步骤3 每条人工鱼每完成一次寻优,BestY就与besty比较,若BestY优于besty,首先用BestY去更新besty,同时将记录besty所对应的bestx,然后转步骤4;反之,若BestY没有besty优,不用更新,直接转步骤4。
步骤4判断是否满足结束条件gen≤max gen,若满足,则返回到步骤2继续执行;反之,若不满足gen≤max gen,则转步骤5。
步骤5 算法结束。结束时,besty中即为所求函数最优值,而bestx中记录的就是besty所对应的自变量值。
算法1中的聚群和追尾行为随机移动算子采用了粒子群算法的思想进行改进,利用粒子群算法有显著的全局搜索能力优点,能够使得算法1跳出局部最优,进而求得最优问题的全局最优值;采用以概率e-r改进觅食行为随机移动算子,提高了算法1的计算精度;采用限制随机移动范围于定义区间的方法,能够提高算法1的收敛速率。采用粒子群算法思想,以概率移动的思想和限制移动范围相结合方式改进随机移动算子,加快了算法1收敛速率,提高了鲁棒性以及求解的计算精度。
4 包含自适应扰动项的改进人工鱼群算法
在AFSA算法中的觅食、聚群和追尾行为中,均出现随机移动一步的现象,它会使得算法陷入局部最优,降低收敛效率和搜索效率。为了克服AFSA算法的缺点,本文提出了包含自适应扰动项的改进人工鱼群算法(ADI-AFSA)。
4.1 ADI-AFSA算法思想
ADI-AFSA算法主要是对觅食、聚群和追尾行为中随机移动算子进行改进,具体做法是在觅食、聚群和追尾行为中添加一项扰动,让它跳出局部最优,进一步搜索到全局最优值,从而达到加快收敛速率和提高搜索效率的目的。改进后觅食行为随机移动算子描述如下:

改进后的聚群行为随机移动算子描述如下:

改进后的追尾行为随机移动算子描述如下:

其中,式(4)、(5)和(6)中(1-i/try_number)是扰动项,i是1~1-i/try_number的整数变量,随着当前第多少次尝试的改变而改变,因此叫做自适应扰动项;式(5)中Xc是中心位置;式(6)中Xmax是探索其视野范围内最优的一个值。并且同样限制觅食、聚群和追尾行为中向前移动一步的范围,具体的做法:当>Xmax时,取;当<Xmin时,取=Xmin;这样就在定义区间[Xmin,Xmax]内。同理也采用公告牌,用于记录最优值。
4.2 ADI-AFSA算法描述
首先初始化参数,然后执行聚群行为、觅食行为、追尾行为和随机行为,同样采用公告牌策略,详细的描述见算法2。
算法2 包含自适应扰动项的改进人工鱼群算法(ADI-AFSA算法)
步骤1初始化人工鱼群中参数和公告牌信息,包括:N、Visual、try_number、δ、max gen、gen=1、BestY、BestX;公告牌中参数:besty、bestx。
步骤2执行聚群行为、觅食行为、追尾行为和随机行为,具体在执行觅食、聚群和追尾行为中随机移动算子时,分别按照式(4)、(5)和(6)所给的移动算子执行。
步骤3 每条人工鱼每完成一次寻优,BestY就与besty比较,若BestY优于besty,首先用BestY去更新besty,同时将记录besty所对应的bestx,然后转步骤4;反之,若BestY没有besty优,不用更新,直接转步骤4。
步骤4 判断是否满足结束条件gen≤max gen,若满足,则返回到步骤2继续执行;反之,若不满足gen≤max gen,则转步骤5。
步骤5 算法结束。结束时,besty中即为所求函数最优值,而bestx中记录的就是besty所对应的自变量值。
算法2中的聚群、觅食和追尾行为随机移动算子均采用了增加扰动的思想进行改进,能够使得算法2跳出局部最优,进而求得最优问题的全局最优值;采用限制随机移动范围于定义区间的方法,能够提高算法2的收敛速率。采用带有扰动和限制移动范围移动的结合方式改进随机移动算子,加快了算法2收敛速率和搜索效率,提高了求解的计算精度以及具有较好的鲁棒性。
5 PSO-AFSA和ADI-AFSA算法收敛性分析
命题1 当时间趋于无穷时,PSO-AFSA和ADI-AFSA算法具有全局渐近收敛性。
证明因为在PSO-AFSA和ADI-AFSA算法的觅食、聚群和追尾行为中,个体在寻优过程中有信息交换和相互学习的行为,即有“社会协作[19]”;还有个体主动或被动地调节自身的状态以更好地适应环境,即有“自我适应[19]”;以及使用公告牌策略,即有“竞争[19]”。从PSO-AFSA和ADI-AFSA算法描述中可知,改进的PSO-AFSA和ADIAFSA算法满足群智能算法统一框架中迭代搜索过程中的社会协作、自我适应和竞争3个基本条件,即可以将PSO-AFSA和ADI-AFSA算法归到智能算法统一框架中,由智能优化统一框架算法性能所列出的收敛性结论[19]可知,当时间趋于无穷,基于统一框架的保优性群体智能优化(Population-based Intelligent Optim ization,PIO)算法具有全局渐近收敛性,即命题1成立。
引理若一个算法满足如下两个条件[8,20-21]:
(1)对可行域内的任意两个点X和X′,X′是X通过进化为η精度可达的;
(2)算法采用的是精英保存策略,即最优个体是单调的,则算法以概率1收敛到具有η精度的全局最优解。
命题2若待求解的优化问题在搜索空间域中连续,则PSO-AFSA和ADI-AFSA算法以概率1收敛到待求解优化问题的全局最优解。
证明因为在PSO-AFSA和ADI-AFSA算法的行为中有“自我适应”,即存在进化的过程,使得PSO-AFSA和ADI-AFSA算法满足引理条件(1);在PSO-AFSA和ADIAFSA算法中均采用公告牌的策略,因此所记录的优化函数值构成的数列是一个单调的数列,从而使得算法中鱼群最优个体状态是单调的,满足引理条件(2),即命题2得证。
6 仿真实验
为了验证所提出的PSO-AFSA和ADI-AFSA算法的计算精度、鲁棒性、收敛速率以及搜索效率的优越性,下面将具体介绍测试函数及参数的选取和实验结果分析。
6.1 测试函数及参数的选取
为了验证提出的基于粒子群算法的人工鱼群算法(PSO-AFSA)和包含自适应扰动项的改进人工鱼群算法(ADI-AFSA)的性能,本文采用文献[17]附录B中所提供的公认测试函数集,因在求解最大值与最小值之间可以添加符号相互转化,所以本文选取了其中的5个求最大值的多峰函数进行测试。具体所选取的测试函数如下:
(2)max F2(x,y)=x sin(4πx)-y sin(4πy+π+1),x,y∈[-1,2]。max F2(1.628 9,2)=3.309 9,即在点(1.628 9,2)处,F2取得全局最大值3.309 9。
(3)max F3(x,y)=cos(2πx)×cos(2πy)×e-(x2+y2)/10,x,y∈[-1,1],max F3(0,0)=1,即在点(0,0)处,F3取得全局最大值1。
运行环境:处理器Intel®CoreTMi3-2350M CPU@2.30 GHz,内存为4.00 GB,MATLAB版本为matlabR2012b。对于测试函数F1、F2、F3、F4和F5所选用的人工鱼群算法参数受到文献[8,13,18]的启发并通过大量的对比实验分析,所选参数的具体值如表1所示。

表1 人工鱼群算法参数设置
6.2 实验结果分析
根据表1设置的参数,以及考虑到对比性,针对测试函数F1、F2、F3、F4和F5所选用的参数均相同。每种算法对每个测试函数进行20次实验,记录下20组实验值。得出测试函数F1、F2、F3、F4和F5在AFSA、LM-AFSA、SA-AFSA、PSO-AFSA和ADI-AFSA等5种算法的寻优结果,如表2所示。
针对不同的测试函数,相同的测试参数,通过实验仿真表明:
(1)从表2仿真结果中最佳优化值来看,对于测试函数F1、F2、F3、F4和F5,PSO-AFSA和ADI-AFSA算法得到的结果均比AFSA、LM-AFSA和SA-AFSA算法得到的结果理想,显示出改进算法的明显优势。其次从最差优化值和平均优化值来看,改进算法得到的结果在不同测试函数下,也显示出一定优势。另外,对于同一测试函数F1来说,改进算法得到的最佳优化值1.000 00比文献[5]中给出的全局最优值0.999 20要精确,已达到理论的分析值。对于测试函数F2来说,算法得到的最佳优化值3.309 89更接近文献[17]给出的函数全局最优值3.309 90。对于测试函数F3和F4来说,改进算法得到的最佳优化值更接近文献[17]中给出的全局最优值1.000 00。对于测试函数F5来说,改进算法得到的最优值更接近文献[17]中给出的全局最优值186.730 91。这些结果说明改进算法具有更高的计算精度,能够搜索到全局最优值。
(2)对于测试函数F1、F2、F4和F5,与其他4种算法相比,PSO-AFSA算法所得到的优化值方差更小,说明改进的PSO-AFSA算法具有更好的鲁棒性。在测试函数F1和F5中,ADI-AFSA算法所得到的优化值方差比AFSA、LM-AFSA和SA-AFSA算法要小,表明ADI-AFSA算法也表现出较好鲁棒性的优点。

表2 仿真结果
(3)对于测试函数F1、F2、F3、F4和F5,改进的PSO-AFSA和ADI-AFSA算法的平均迭代次数小于AFSA、LM-AFSA和SA-AFSA算法的平均迭代次数,说明改进的PSO-AFSA和ADI-AFSA算法具有更好的收敛速率和搜索效率。
7 结束语
针对人工鱼群算法在求解多峰函数优化问题时,搜索全局最优解的能力不足,求解精度不够,鲁棒性较差以及收敛速率较慢和搜索效率较低的缺点,提出基于粒子群算法的人工鱼群算法(PSO-AFSA)和包含自适应扰动项的改进人工鱼群算法(ADI-AFSA)两种算法,主要是以概率随机移动的思想改进觅食行为中随机移动算子,利用粒子群算法的思想去改进聚群行为和追尾行为中的随机移动算子,以及利用扰动项的思想改进觅食行为、聚群行为和追尾行为中随机移动算子。并且严格限制随机移动算子在定义区间[Xmin,Xmax]内,最后利用公告牌记录全局的最优值,并从理论上分析了两种改进算法的收敛性。通过对5个典型的多峰函数进行实验仿真,结果表明改进随机移动算子能够进一步提高求解多峰函数最优值的求解精度,克服了人工鱼群算法求解精度不足和搜索全局最优值能力有限的缺点。而且改进了的随机移动算子使得提出的算法与人工鱼群算法及传统算法相比,具有更好的鲁棒性,以及更好的收敛速率和搜索效率。
[1]李晓磊,邵之江,钱积新.一种基于动物自治体的寻优模式:鱼群算法[J].系统工程理论与实践,2002,22(11):32-38.
[2]李晓磊.一种新型的智能优化方法——人工鱼群算法[D].杭州:浙江大学,2003.
[3]赵吉,孙俊,须文波.一种求解多峰函数优化问题的量子行为粒子群算法[J].计算机应用,2006,26(12):2956-2960.
[4]刘佳,刘丽娜,李靖,等.基于模拟退火算法的改进人工鱼群算法研究[J].计算机仿真,2011,28(10):195-198.
[5]张严,楚晓丽.一种改进的人工鱼群算法[J].计算机系统应用,2011,20(5):199-201.
[6]邓涛,姚宏,杜军.多峰函数优化的改进人工鱼群混合算法[J].计算机应用,2012,32(10):2904-2906.
[7]Chen Z H,Tian X Q.Artificial fish-swarm algorithm with chaos and its application[C]//Proceedings of the 2nd International Workshop on Education Technology and Computer Science,2010:226-229.
[8]曲良东,何登旭,黄勇.一种新型的启发式人工鱼群算法[J].计算机工程,2011,37(17):140-142.
[9]范玉军,王冬冬,孙明明.改进的人工鱼群算法[J].重庆师范大学学报:自然科学版,2007,24(3):23-26.
[10]Luo Y X.The novel compound evolutionary optimization algorithm with hybrid discrete variables and its application to mechanical optimization[J].Advaned Macterials Research,2010(97/101):3276-3280.
[11]曲良东,何登旭.混合变异算子的人工鱼群算法[J].计算机工程与应用,2008,44(35):50-52.
[12]厍向阳,朱命昊,赵亚敏.求解0/1背包问题的改进人工鱼群算法研究[J].计算机工程与应用,2011,47(21):43-46.
[13]姚祥光,周永权,李咏梅.人工鱼群与微粒群混合优化算法[J].计算机应用研究,2010,27(6):2084-2086.
[14]Zheng Genrang,Lin Zhengchun.A w inner determination algorithm for combinatorial auctions based on hybrid artificial fish swarm algorithm[J].Physics Procedia,2012,25:1666-1670.
[15]Neshat M,Sepidnam G,Sargolzaei M,et al.Artificial fish swarm algorithm:a survey of the state-of-the-art,hybridization,combinatorial and indicative applications[J/OL].(2012-05)[2013-12-31].http://dx.doi.org/10.1007/s10462-012-9342-2.
[16]Zhan Zhihui,Zhang Jun,Chung H S H.Adaptive particle swarm optimization[J].IEEE Transactions on Systems,M an,and Cybernetics,2009,39(6):1362-1381.
[17]江铭炎,袁东风.人工鱼群算法及其应用[M].北京:科学出版社,2012.
[18]史峰,王辉,郁磊,等.MATLAB智能算法30个案例分析[M].北京:北京航空航天大学出版社,2011.
[19]王凌,刘波.微粒群优化与调度算法[M].北京:清华大学出版社,2008.
[20]Back T.Evolutionary algorithms in theory and practice[M].New York:Oxford University Press,1996.
[21]刘淳安,王宇平.约束多目标优化问题的进化算法及其收敛性[J].系统工程与电子技术,2007,29(2):277-280.

