基于DOA测量的多目标位置信息场定位精度分析

马贤同，罗景青

1.电子信息控制重点实验室，合肥230037

2.电子工程学院，合肥230037

无源定位属于被动定位，系统具有很好的隐蔽性，不易受到干扰和攻击，是目前定位研究的主要方向。目前主要的无源定位技术中应用的最广泛的是：测向交叉定位法[1]和时差定位法[2-3]。很多学者对复合定位法进行了研究，主要包括联合利用方位角与时间差信息的DT法[4]、联合利用方位角与多普勒（Doppler）信息的DF法[5]等。

相较于上述定位方法，测向交叉定位法具有全方位、快速、探测距离远、抗干扰能力强等优点。在实战中，侦察系统往往在同一时间面对的是空间多个辐射源的复杂电磁环境，有时需要对多个同类辐射源同时进行定位。现有的诸多定位方法都是针对单目标定位的，它们在进行定位计算之前，都要知道测量参数是关于某个确定目标的。文献[6]直接利用观测站得到的方位数据，用寻找最大可能密度区域的方法来确定目标的位置，但只研究了一个目标的情况。而位置信息场定位法不需要对测量参数按目标进行分类，同时确定目标数目和目标的位置。例如，对测得的一组方位角数据，不知道这些方位角数据是关于一个目标的还是两个目标的或者更多目标的，这时可用位置信息场定位法确定目标数目和目标的位置。在此基础上，对基于DOA信息的位置信息场定位方法进行了精度分析，通过理论推导得到了定位误差的协方差矩阵，运用椭圆概率误差与定位误差几何分布来描述定位精度。研究结果为该类系统的技术作战运用提供了理论支持。

1 目标位置信息场定位法原理

定义在指定区域内关于感兴趣目标或目标群位置分布的函数，为目标位置信息场函数，简称目标位置信息场或位置信息场。目标位置信息场是一个标量场，是关于目标或目标群位置分布特征的一个描述。在二维平面或三维空间甚至更高维空间，关于目标和目标群的本体位置特征可用一个精确位置概率分布密度来表达：

其中，X表示所关心的可能存在目标的位置，NT为目标的个数，αi为在位置Xi存在目标的相对可靠性因子，KX为归一化系数，而δ(·)为犾拉克函数。

一般，式（1）很难得到，而可以得到的只是式（1）的一个估计。当获得了一批观测（信号测量数据或测量参数集）Z后，由于观测的有限时域特性和有限频域特性，得到的结果是式（1）与一些函数的卷积：

式中，fX(X|Z)就是基于观测Z的关于目标的位置信息场函数，…，NT为当目标作为单目标时Xi的估计结果，是Z的函数。是某个在X=处取极大值且只有一个极值的实函数。Z实际上是一观测空间，它可以是任何与目标位置有关的观测值的集合，可以是多个观测矢量的组合。之所以给出单目标时的估计结果，是因为在多目标情况，由于各目标后验概率密度函数的互相影响，其估计结果可能不再具有与式（1）相对应的形式。

需要指出的是，式（1）中的Z可以是多个方位或方位和距离或功率或衰减因子及相关参数，也可以是到达时间、到达时间差、频差、相位差、相位差变化率、方位变化率等等，当然还可以是直接时域采样数据[7]、直接频域采样数据[8]，甚至可以是位置取样值本身。根据Z，求得fX(X|Z)，并从中分析出目标的个数、目标的位置的方法，称之为位置信息场定位法[9]。

2 基于DOA测量的位置信息场定位法

2.1 观测模型

一般，无论是无源定位，还是有源定位，总是靠多次测量与目标位置有关的参数或信号后，对目标位置进行确定（估计）的。对只测向定位（以方位角为例）而言，P个观测站所得到的观测值Z可描述成多个独立测量的方位角矢量的组合：

其中M≥1，表示独立观测的次数。而相应于zm的目标“响应”函数hm(XE)为：

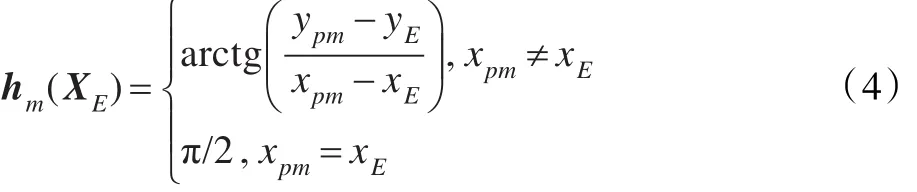
其中，m=1，2，…，M，XE=(xE，yE)为目标位置坐标，XE可能是一个确知参量，也可能是多个确知参量，还可以是随机参量。对于多目标的情况，它可以是任意一个目标的位置坐标。以两个目标（用1和2表示）为例，(xE，yE)可能是目标1的坐标，也可能是目标2的坐标。式（4）中(xpm，ypm)， p=1，2，…，P，为在获得第m组测量值时观测站p所对应的位置。一般地，对阵列测向系统而言，方位角定义为阵列法线方向到辐射源波达方向的夹角。假设阵列基线方向与X轴方向一致，如图1所示。

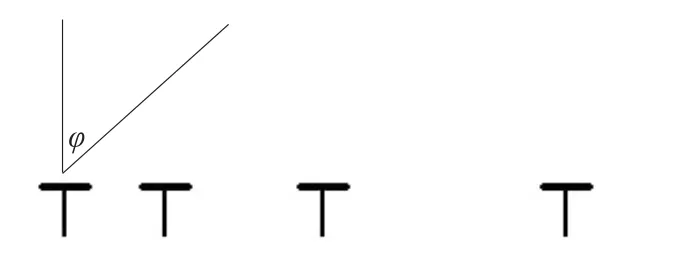
图1 阵列布局示意图

每个独立的观测量一般均是受测量噪声污染后的与目标位置有关的函数：

其中，hm(XE)为目标对应于测量zm无噪时的“响应”，其形式由式（4）确定，而vm是观测量zm的测量误差，假定测量噪声是零均值的，其协方差矩阵为：

设XE的先验概率密度为p0(X)，则可定义目标位置信息场为：

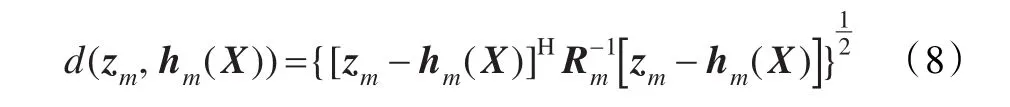
是观测矢量zm与场内点X处目标响应hm(X)的标称化距离（欧氏距离）。为一代价函数，而

2.2 代价函数的选取

对可能存在目标的一个感兴趣的区域，就某一观测站而言，区域内的每一点都可以得到相对于该观测站的一个方位角，这些方位角组成一个集合，用B表示。对于观测站测得的每一个方位角z而言，z∈B。B中一些方位角是与z离得比较“近”的，一些则离得比较“远”。在对目标进行定位的过程中，就需要对B中的方位角进行处理，使得与z离得比较“近”的方位角信息对定位结果的“贡献”大，使与z离得比较“远”的方位角信息对定位结果的“贡献”小。

设方位角测量误差的均值为0，标准差为σθ。对某一观测站得到的每一个方位角z，式（8）可以写为：

其中|| • 表示取绝对值，且

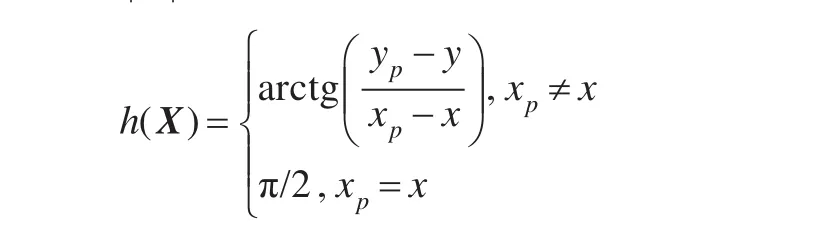
h(X)表示区域X内任意一点(x，y)对应于观测站(xp，yp)的方位角。则代价函数可以定义如下：

其中，γ为一门限。

由于式（10）代价函数的选取，在一定程度上突出了有价值信息对定位结果的“贡献”，对不可靠的或者价值小的信息的“贡献”进行了弱化。

3 基于DOA测量的位置信息场定位精度分析

位置XE的估计是使式（7）最大的估计，结合代价函数，在目标附近区域内，可以推得，使式（7）最大的估计也是使

取最小值的估计。

其中，当XE=(xE，yE)T时：

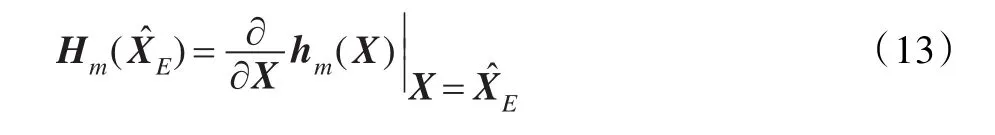
作近似处理：

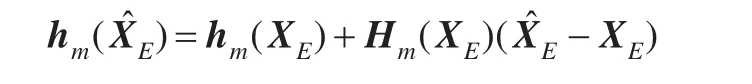
且假定：

再考虑到zm=hm(XE)+vm，由式（12）可得：

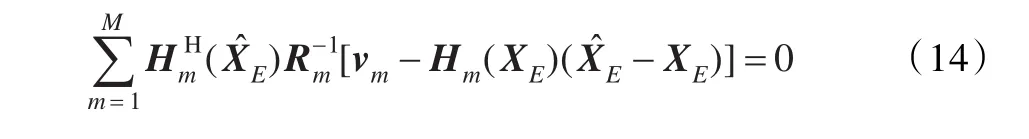
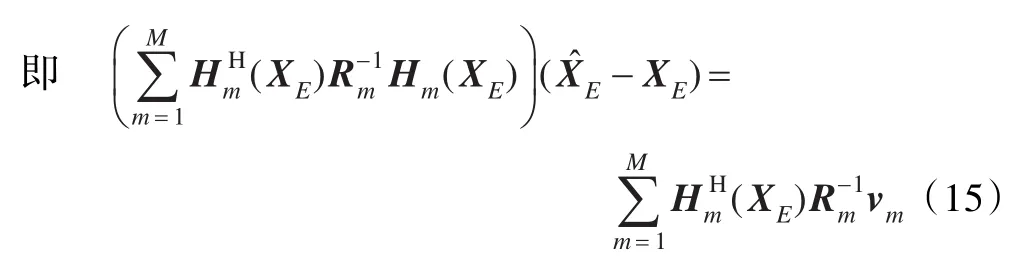
对式（15）两边求均值，可得：

对式（15）两边求协方差矩阵，可得：

其中PXE为定位误差协方差矩阵，化简式（17）可得：

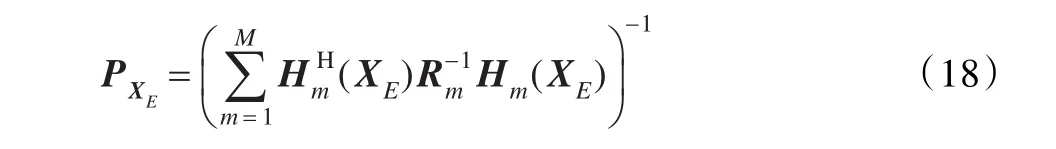
令最终计算得到的定位误差协方差矩阵为：

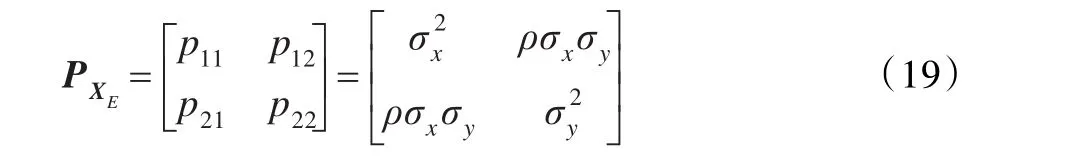
3.1 椭圆概率误差表示法

根据协方差矩阵PXE，可以确定定位误差椭圆关于x， y的方程为：

其中，D2=-2 ln(1-P)，通常将P=0.5所对应的椭圆称为椭圆概率误差；xE、 yE为目标辐射源坐标值。定位误差椭圆的半长轴a、半短轴b和长轴方向θ的计算参见文献[10]。

3.2 定位误差几何分布表示法

根据式（19），则定位误差的几何分布（Geometric Dilution of Precision，GDOP）可表示为：

根据GDOP分布图及测向定位原理可以得出，误差最小的定位方向应位于基线的法线方向，下面的仿真实验将会验证这一点。

4 仿真实验

假设三个观测站对辐射源进行测向定位，观测站1的位置为(-30 km，3 km)，得到关于辐射源的方位角为29.8°和47.2°；观测站2的位置为(0 km，3 km)，得到关于辐射源的方位角为8.3°和27.5°；观测站3的位置为(30 km，3 km)，得到关于辐射源的方位角为－17.9°和0.5°，称相邻两个观测站的距离为基线长度，此时基线长度l为30 km。图2（a）是利用观测站得到的方位角画出的测向定位线，其中“o”表示观测站的位置，图2（b）是运用位置信息定位的效果图，可以确定目标的个数为2，目标的位置分别为(9 km，70 km)和(30 km，59 km)。

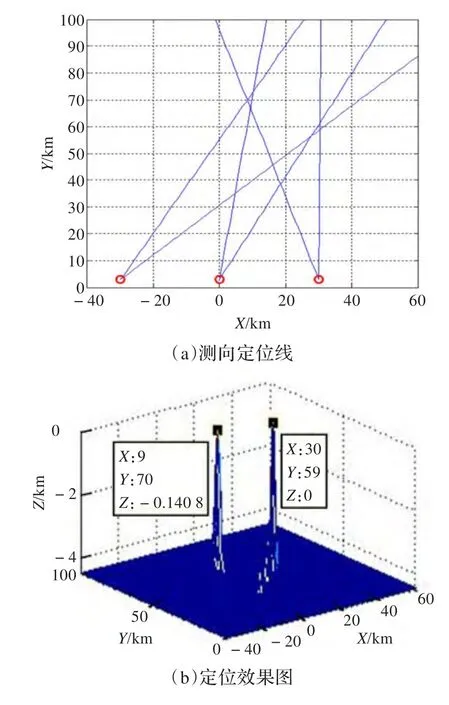
图2 位置信息场定位

（1）测向精度对定位精度的影响

观测站的位置同上不变，图3绘制了测向精度σθ分别为1°和0.5°时的定位精度分布图。图3中（a）采用椭圆概率误差表示法，（b）采用定位误差几何分布表示法，分别描绘了观测站周围100 km内的定位误差分布情况。从图中可以看出：随着测向精度提高，定位精度明显提高，测向精度对定位精度产生了主要的影响。

（2）基线长度对定位精度的影响

设观测站1的横坐标为分别为－50 km和－70 km，观测站2的位置分别为50 km和70 km，其他条件不变，即考虑基线长度l为50 km和70 km的情况；测向精度σθ为1°。定位精度分布如图4所示。结合图3和图4可以看出：随着基线长度的增长，定位精度明显提高，基线长度对定位精度产生了主要的影响。

5 总结

针对不可区分的多个同类辐射源定位的问题，由于很难分辨某个测量参数是关于某个确定目标的，现有的方法也就无法获得辐射源目标的位置信息；而位置信息场定位法可以对不可区分的多个同类辐射源定位，同时确定目标数目和多个目标的位置。在此基础上，对基于DOA测量的位置信息场定位方法进行精度分析，仿真实验运用椭圆概率误差和定位误差几何分布来描述定位精度。结合理论指导与仿真实验，说明了位置信息场定位法是一种有效的多目标定位方法。得出的若干结论，为该类系统的技术作战运用提供了理论支持。

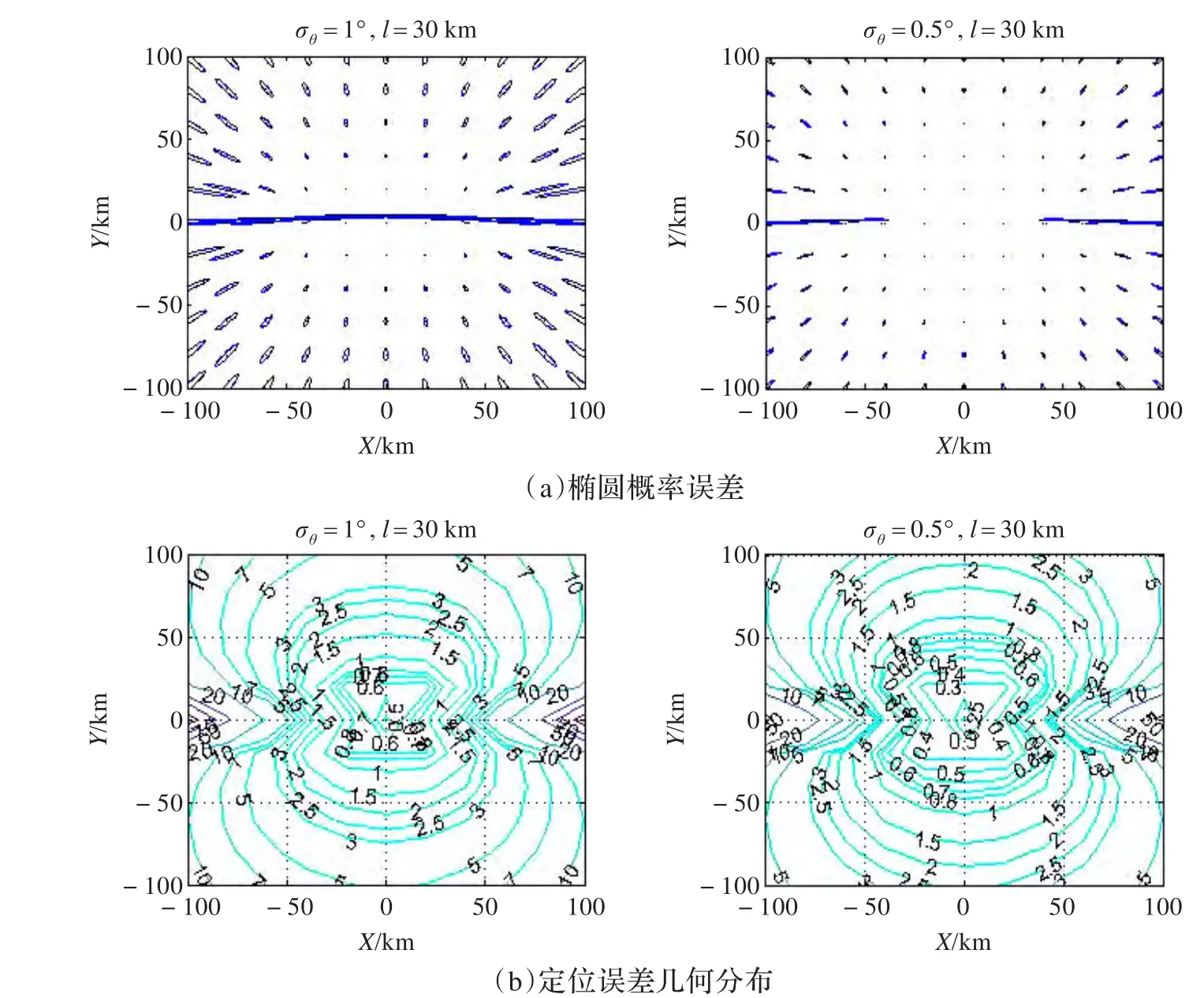
图3 测向精度单独对定位精度的影响

图4 基线长度单独对定位精度的影响

[1]Xiu J J，He Y，Wang G H，et al.Constellation of multi-sensors in bearing-only location system[J].IEE Proc-Radar Sonar Navig，2005，152（3）：215-218.

[2]Wang Xu，He Zishu.Target motion analysis in three-sensor TDOA location system[J].Information Technology Journal，2011，10（6）：1150-1160.

[3]Yeredor A，Angel E.Joint TDOA and FDOA estimation：a conditional bound and its use for optimally weighted localization[J].IEEE Trans on Signal Process，2011，59（4）：1612-1623.

[4]Li Z H，Feng D W，Sun Z K，et al.Passive location using time of arrival along with direction of arrival and its changing rate[C]//Proceedings of IEEE International Conference on Robotics，Intelligent System s and Signal Processing，Changsha，China.[S.l.]：IEEE，2003：261-265.

[5]贾兴江，周一宇，郭福成.多运动站测角频差无源定位方法研究[J].国防科技大学学报，2011，31（1）：76-80.

[6]Zhang Z H，Huang G M，Wang C P，et al.Passive location algorithm based on maximum probability density[C]//Proceedings of Conference on Information Engineering and Computer Science，2009：1-4.

[7]Amar A，Weiss A J.Localization of narrow band radio emitters based on Doppler frequency shifts[J].IEEE Trans on Signal Process，2008，56（11）：5500-5508.

[8]Weiss A J.Direct geolocation of wide band emitters based on delay and Doppler[J].IEEE Trans on Signal Process，2011，59（6）：2513-2521.

[9]罗景青.目标位置信息场分析定位法[J].电子工程学院学报，2012，31（2）：1-4.

[10]杨士英，罗景青.利用误差椭圆消除虚假定位的算法研究[J].电子对抗技术，2004，19（5）：3-6.