城市道路网络动态优化选择方法研究
李晓丹
1.上海应用技术学院计算机科学与信息工程学院,上海201418
2.上海济祥智能交通科技有限公司事业部,上海200092
1 引言
路径诱导系统是一个复杂多目标的大系统。它向不同用户分时、分区提供不同路径信息服务,一种诱导信息只适应一定区域、一定时间和一定的用户,当其中一个条件变化时,诱导信息便不再适用。在动态路径诱导时,需要着重考虑以下几个问题:
(1)路径的实时性,降低计算的时间复杂度。
(2)路径的动态性,考虑动态交通状态信息对路径的影响。
(3)驾驶员路径选择行为,考虑人的出行习惯等因素的影响,而不仅仅是数学意义上的距离最短或时间最短的路径。
在动态路径诱导时,问题(1)是首先需要解决的,这决定了算法的实用性,国内外在算法实时性方面的研究成果也较多,主要是从道路网络的表达方式优化(即降低算法搜索路网的规模,如采用路网分层分解方法[1-6]、矩形区域搜索方法[7]、椭圆区域搜索方法[3]等),网络存储结构优化[5,7],搜索策略的优化(启发式算法[2]、基于交通流融合的蚁群算法[1]、改进Dijkstra算法[4-5]等)等方面进行研究,从不同程度降低了路网的复杂度。问题(2)也是计算动态路径必须要解决的问题,当前大部分的算法中都考虑了路段行程时间的估计和预测[2-3,5,7],用于计算动态的路阻函数。将问题(3)考虑到动态路径搜索算法中的研究并不多见,文献[4]对此进行了详细的解析,并基于路网分层分解方法实现动态路径诱导算法,但在路网分层方面没有进一步划分路径搜索区域,高层路网的规模依然很大,而且没有将实时交通状态考虑进去。
据以上分析可知,当前的动态路径诱导法研究,完全充分考虑上述三个问题的研究不多见,要么是对降低计算时间复杂度方面研究不够,要么是未考虑现实中驾驶员的路径选择习惯。本文即是在综合考虑路径实时性、动态性和驾驶员选择行为的基础上,提出了面向动态路径诱导的路网动态分层优化方法。
本文研究遵循这样的驾驶员出行行为假设:出行者大多数愿意选择那些他们比较熟悉,道路等级较高,连通性能较好的次优路径,而不是单纯的距离最短路径。
2 路网实时交通状态判别
能够及时准确地获取实时交通状态信息,是保障动态路径达到出行者期望的重要信息来源。出行者一般期望推荐的路径上没有严重的拥挤,行程时间在可接受的范围内[4],即为最优路径,因此它并不是严格数学意义上的时间最短路或距离最短路,相反它具有更符合驾驶员行为的现实意义。
2.1 连线拥挤度模型
(1)城市交通网络模型建立
交通网络可定义为:n个交叉口和交叉口间的路段组成交通网络G=(I,L)。其中I=(i1,i2,…,in)表示路口集;表示与路口相关的路段集,Lij=<i,j>表示存在一条从路口i到路口j的路段。
在建立交通网络模型的时候,需要考虑将交叉口参数归入路段参数,共同作为交通网络连线的权,从而可以计算每个连线的拥挤系数。其中,交叉口称为网络的节点,交叉口之间的连线即路段称为网络的连线。其模型示意图如图1所示。
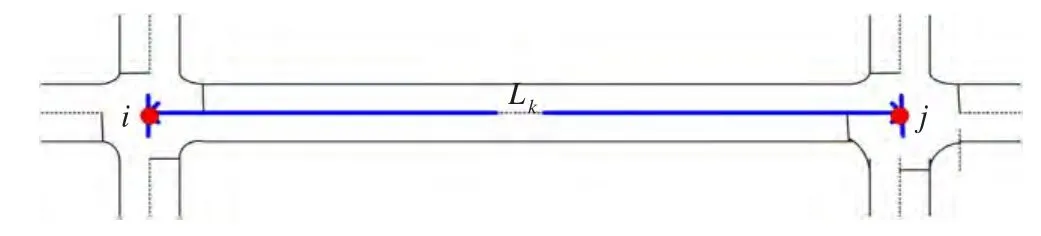
图1 交通网络连线节点模型示意图
(2)连线拥挤度概念
“连线拥挤度”较明确地反映了交通状态,且最容易被人理解和接受。但是拥挤度并不是一个可直接测量而得的数据,必须通过其他交通参数的转换或计算获得。
本文对“连线拥挤度”进行如下定义[8]:

其中:

上式中,λ为连线拥挤度,可以表示连线k的拥挤程度,值越大表示拥挤程度越严重;Tk为连线k上车辆的实际平均行程时间;Tk0为连线k上车辆按照最大限速行驶的行程时间;Lk为连线k的实际长度;vˉk为连线k上车辆的平均行驶速度;vˉki为连线k上第i辆车的平均行驶速度;vˉk0为连线k上允许或设计的车辆的最大行驶速度;n为连线k上的车辆数(这里假设n满足最小样本量)。
式(2)中,连线实际平均行程时间,可采用移动检测设备,如浮动车数据,作为数据源来计算获取。一般的,浮动车都可以直接获得车辆的瞬时行驶速度,加上与精确电子地图的地图匹配,可以获得其在连线k上的平均行驶速度,具体算法可参阅文献[9-10]等。
2.2 交通状态判别方法

当Tk≤Tk0时,,即λ≤0时,实际行程时间小于或等于期望时间,即无延误产生,为用户最期望状态——畅通状态。
当Tk>Tk0时,,即λ>0时,实际行程时间超过期望时间,即发生了延误。λ取值越大,延误越大,交通状态越拥挤,道路服务质量越低下。
以城市主干道最大限速60 km/h为例,那么:
式(1)可进一步推导为:
根据λ的取值,判断交通状态的流程如图2所示。
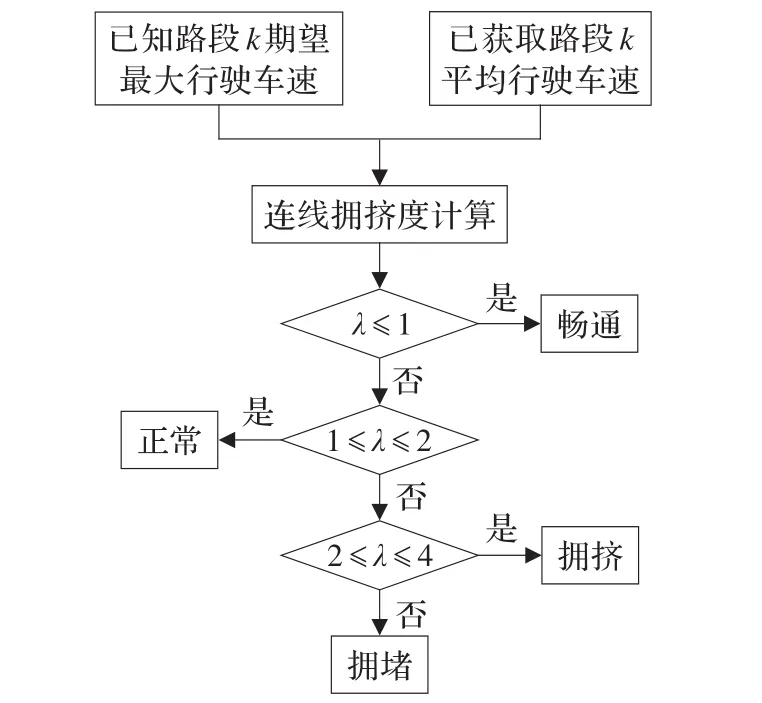
图2 交通状态等级判别流程图
3 考虑实时状态的道路动态分级
这里的“道路动态分级”是依据对驾驶员的出行行为假设,对道路优先级别的一个动态分级。它本质上并不改变道路原有的道路等级,只是对路网分层指标的一个动态量化过程。
正是由于交通状态的时变性,城市高等级道路(主干道)并不总处于优先选择的地位,而城市低等级道路(支路、次干道)也并不总处于无优势的地位。一般来说,高等级道路在路径选择过程中具有较高的权重,从这个意义上讲,本文将实时的交通状态因素考虑到道路优先等级再确定过程中,以便给出所有城市道路合理的权重等级。
本文依据驾驶员选择路径道路等级优先顺序的一般规律,将实时交通状态对道路优先等级的影响权重ω设定为:畅通,ω=1;正常,ω=0.8;拥挤,ω=0.4;拥堵,ω=0。
假设道路的优先等级指数G可以量化为:[2,1],分别对应:[高层道路,低层道路],那么,基于交通状态影响权重系数的道路优先等级指数G′可表达为:
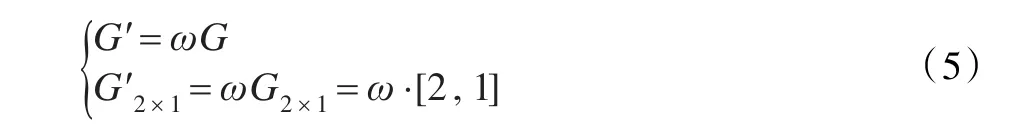
下面以当前道路优先等级为高等级道路,加权后道路优先等级指数的确定方法示例:
若当前判断路段为畅通,则路段道路优先等级指数维持不变,即G′=G=1×2=2;
若当前判断路段为正常,则新的道路优先等级指数表达为G′=0.8×2=1.6;
若当前判断路段为拥挤,则新的道路优先等级指数表达为G′=0.4×2=0.8;
若当前判断路段为拥堵,则新的道路优先等级指数表达为G′=0×2=0。
依次类推,可以对所有不同等级的道路,计算考虑交通状态影响权重系数下的新的道路优先等级指数。
从中可以看出,由于路段交通状态的不同,改变了道路优先等级的原始数值。即使高等级的道路,由于其交通状态是拥堵的,驾驶员也不会优先选择这些道路。
交通状态的影响结果只考虑两种情况:加入高层网络和不加入高层网络,因此将交通状态等级模糊为二级:正常和拥挤。按照第2章讨论的城市道路交通状态判别方法,和本节讨论的考虑交通状态影响下的道路优先等级确定方法,可以建立如图3所示的对应关系。
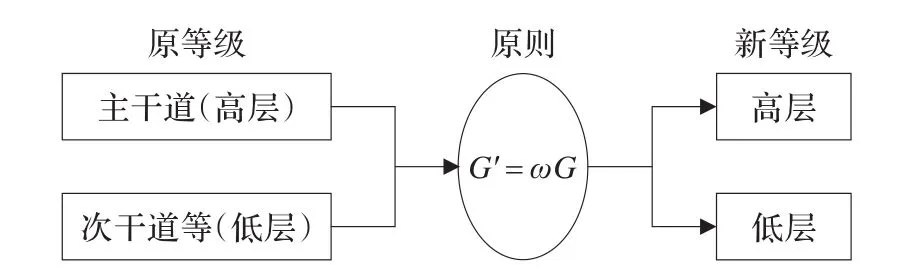
图3 考虑交通状态的道路动态分级
根据这种对应法则,可以获得城市道路的动态道路优先等级,从而可以划分实时的高层网络。
4 道路网络动态分层及规则
4.1 连线交通相似度的表达
在不考虑起止点位置时,首先是高层网络的计算,也就是说,高层网络是具有一定交通相似度的节点和连线的大集合。高层网络完全是依据道路网络的优先等级和交通状态的综合系数的相似程度积聚而成的。

式中,K为连线交通相似度系数;g为原始道路优先等级指数;s为实时交通状态参数;g′为考虑动态因素的新的道路优先等级指数;ω为交通状态影响权重系数;一般,ω≥0.8时为正常或畅通状态。
4.2 道路网络的动态分层规则
在对道路优先等级进行再确定之后,不考虑实时交通状态影响因素的道路网络分层需要进行局部调整。比如,对于交通拥堵的高等级道路,其行程时间延误增大,与交通畅通的相邻低等级道路(如次干道等)相比,大多数驾驶员会选择低等级道路绕行,这时低等级道路的优先级别升高,可以在网络分层时将其划入高层网络;而在高等级道路恢复交通畅通后,重新划入高层网络,而原来的低等级道路划入低层网络。这个过程就是道路网络的动态分层(如图4)优化过程。
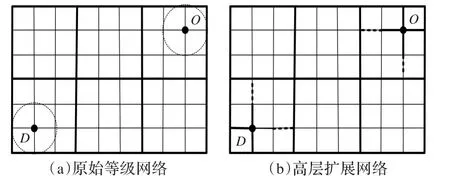
图4 道路网络的动态分层示意图
根据O、D点位置的不同,即O、D点是否是在高层网络,道路网络的动态分层有两种情况:
(1)O、D点在高等级道路上
当O、D点在高等级道路上时,道路网络的动态分层较为简单,即按照上述动态分层优化过程,直接实现道路网络的动态分层。这种情况大部分发生在途中动态路径再规划时,需要重新分层和分区。
(2)O、D点不在高等级道路上
当O、D点不在高等级道路上时,需要考虑必须把O、D点及其所在的和周围相关的连线都划分到高层网络中。这时需要以O点或D点为圆心,以到达周围高等级道路的直线距离为半径,做出圆域,将圆域范围内的次干道、支路等较低等级的道路路段也添加到临时高层网络中,以备最优路径的检索。这种情况一般发生在初始路径规划或途中路径再规划时。
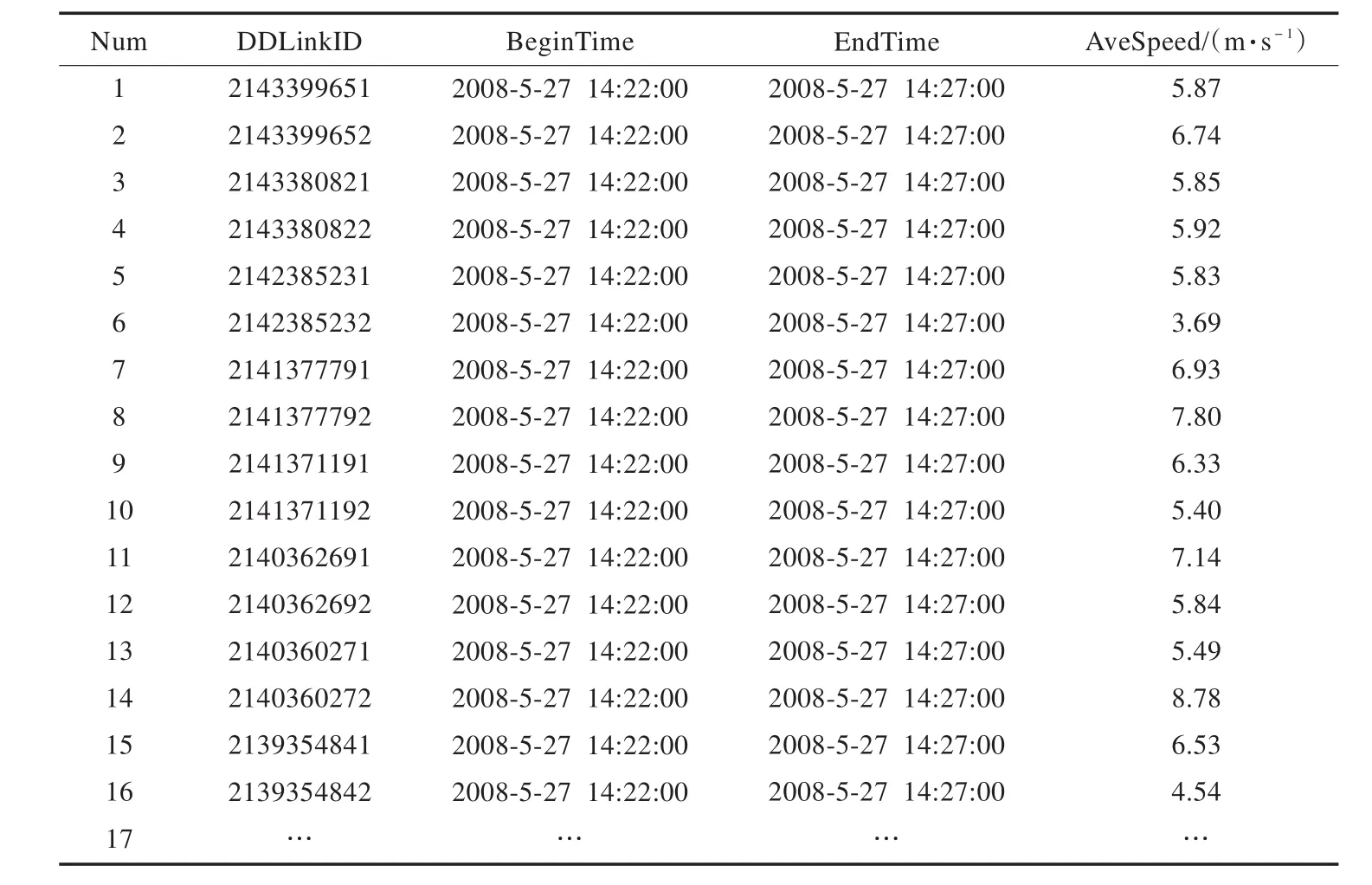
表1 交通状态参数计算表(delinkdtatus)
以上根据道路网络中道路的不同等级特性和实时交通状态信息,将原来的整个道路网络分为两层,采用多层地图的分级搜索技术可实现对搜索空间的控制。基于分层地图的路径搜索算法对道路网络的分层规则要求具有下特征[11-12]:
(1)对不同优化标准,层次可以按照道路优先等级和实时交通状态等级进行划分;
(2)层次细节由高到低逐渐增多,高层次是低层次的子集;
(3)每个层次的道路网络是连通的,对于低层次是肯定的,在高层次中大部分情况下也是连通的,如果不连通,可以通过将低一级层次中的某些路段提取到高一级层次中,使之构成连通网络。譬如,当高层网络中某一路段处于交通拥堵时,其等级指数降低至g′=0.8或g′=0,应将其划入低层网络中,但是此时高层网络处于不连通状态,应该考虑将相邻及其周围的低层网络中等级指数g′≥1或g′≥0.8的路段加入高层网络,使其连通。
按照上述规则,检查道路网络动态分层的高层网络的连通性,使其满足上述规则要求。图4中的虚线即是从低等级道路提取到高层网络中的连线。
5 算例分析
本文选择某市实际路网的部分区域为例,以ESRI公司A rcGIS9.0作为二次开发平台,分析传统Dijkstra算法和分层算法在诱导路径计算时的优劣。
图5中的道路网络为双向道路网络,分别用道路中心线编码后加“1”和“2”来区别表示。图中突出显示的为城市部分主干道网络。
选择某时刻道路网络交通状态计算结果,按照表1结构存储在大型数据库中,本文列出部分数据内容示例。
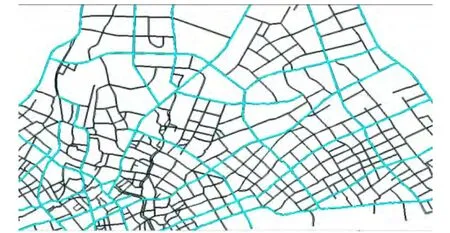
图5 某市部分实际分层路网
表2列出了两种算法路径搜索结果的部分性能对比,从上面的路径结果显示(图6和图7)和表2可以看出传统Dijkstra算法计算复杂度较高,所规划出的路径主要在低级网络上,路径长度最短,平均行车速度低;动态分层算法计算复杂度相对较低,所规划出路径基本都在高层网络上,路径长度稍长,平均行车速度较高。利用动态分层的路径算法,其规划结果更符合实际诱导系统需求,更能体现驾驶员的选路偏好。
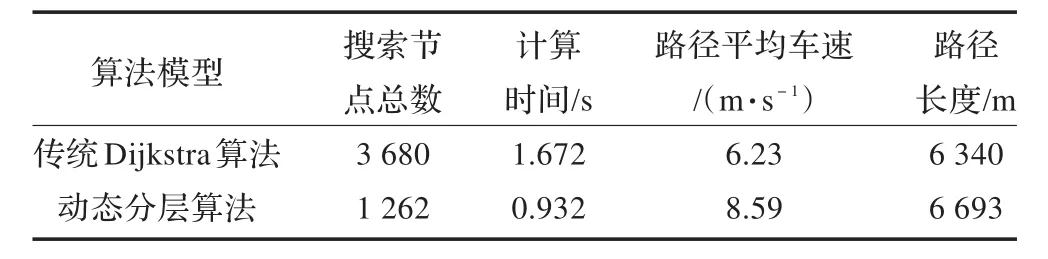
表2 两种算法部分性能对比分析
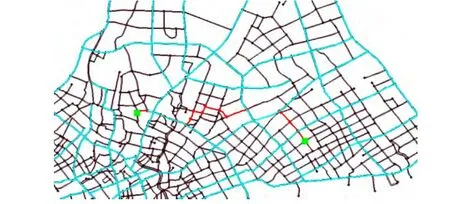
图6 按照传统Dijkstra算法计算路径结果
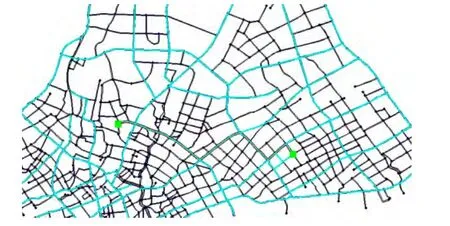
表7 按照道路动态分层算法计算路径结果
6 结束语
本文提出了基于实时交通状态因素的动态道路优先等级指数的确定方法,建立了连线交通相似度的模型,研究了道路网络的动态分层规则和方法,并通过算例进行了简单的验证分析。应该说,基于路网动态分层优化方法的路径选择是有很大优势的,并且更符合驾驶员的选择行为,也与道路规划者期望的道路功能相一致,在实际工程中具有现实意义。
[1]廖志斌.基于网格的城市动态路径诱导系统研究[D].上海:华东师范大学,2007.
[2]刘名龙.城市交通动态路径诱导算法研究及系统设计[D].昆明:昆明理工大学,2005.
[3]苏海滨,王继东,侯朝桢.道路网络分层的快速路径诱导算法[J].火力与指挥控制,2008,33(7):108-111.
[4]曾松.城市道路网络交通导行策略研究[D].上海:同济大学,2000.
[5]范东凯.城市动态路径诱导算法研究[D].西安:长安大学,2006.
[6]Huang Y W,Ning J,Rundensteiner E A.A hierarchical path view model for path finding in Intelligent Transportation System s[J].Geolnformatica,1997,1(2):l25-159.
[7]陈晓红.交通网络动态路径诱导算法研究及其在GIS环境下的仿真实现[D].长沙:长沙理工大学,2005-04.
[8]李晓丹,刘好德,杨晓光,等.城市道路网络交通状态时空演化量化分析[J].系统工程,2008,26(12):66-70.
[9]童小华,陈建阳,吴淑琴.基于GIS和GPS的交通状态参数估计仿真分析[J].同济大学学报:自然科学版,2006,34(1):47-52.[10]张和生,张毅,温慧敏,等.利用GPS数据估计路段的平均行程时间[J].吉林大学学报:工学版,2007,37(3):533-537.
[11]Jagadeesh G R,Srikanthan T,Quek K H.Combining hierarchical and heuristic techniques for high-speed route computation on road networks[J].Computing and Control Engineering Journal,2002(2):120-126.
[12]吴京,景宁,陈宏盛.最佳路径的层次编码及查询算法[J].计算机学报,2000,22(2):184-189.

