连续式桥梁伸缩缝界面黏结性能研究

唐古南，李立寒

(同济大学 道路与交通工程教育部重点实验室，上海 201804)

连续式桥梁伸缩缝是20世纪70年代由英国发展起来的一种新兴的桥梁伸缩缝，由沥青结合料、集料、搭接钢板和填塞料4个部分构成[1]，其结构示意如图1。连续式桥梁伸缩缝兼具施工简便、成本低廉、行车舒适、使用年限长、以及可半幅施工不中断交通等诸多优点，在欧美及东南亚得到广泛应用[2]。该伸缩缝在使用过程中出现的病害主要有：裂缝和车辙[3-4]，而伸缩缝最容易出现裂缝的位置是：①伸缩缝与桥面铺装层的垂直界面；②钢板边缘[5]。

笔者将通过有限元软件ABAQUS计算伸缩缝与桥面铺装层的垂直界面在温度和荷载作用下的受力特征，初步分析界面脱开原因，以及探讨伸缩缝材料模量、铺装厚度、宽度和界面接触条件对界面黏结性能的影响，从而对伸缩缝界面黏结性能提出一些理论性的改善建议。

图1 连续式桥梁伸缩缝结构示意Fig.1 Structure schematic diagram of continuous expansion joint

1 模型建立

1.1 荷载位置

利用有限元软件ABAQUS，建立伸缩缝的二维平面应变模型。为了分析荷载作用下伸缩缝填料与桥面沥青铺装层界面的受力特征(界面即伸缩缝与桥面铺装层的垂直界面，界面位置如图2)，考虑荷载在伸缩缝上3个不同位置，荷载位置如图2，即荷载中心作用于桥面接缝边缘、荷载作用于伸缩缝边缘、荷载中心线与桥面接缝中心线重合。文中施加的荷载为城市道路桥梁A级荷载中最大轴重200 kN对应的接地压强0.67 MPa[6]。

图2 荷载作用位置Fig.2 Location of loads

1.2 材料模型

在建立力学分析模型时，对各材料的力学行为均采用线弹性模型来模拟，相应的表征参数为弹性(回弹)模量E和泊松比μ，各材料参数选取如表1，实验测得20℃伸缩缝填料弹性模量为200 MPa。

表1 材料参数 Table 1 Material parameters

1.3 边界条件

模型的边界条件主要包括两个方面，即模型各表面的位移边界条件和不同材料界面的接触条件。桥梁伸缩缝一般位于桥墩上，伸缩位置的支撑条件为简支，由此伸缩缝竖向位移为0。在横向，混凝土的温度收缩变形将造成伸缩缝横向位移，因此在横向施加初始位移，可以模拟伸缩缝的横向变形。

1)在分析荷载作用时，模型边界条件：固定模型底面竖向位移和模型两边横向位移、不同材料界面完全连续。

2)在分析温度胀缩作用时，模型边界条件：固定模型底面竖向位移和模型一边横向位移，在模型另一边施加水平位移Δ，不同材料界面完全连续。

3)在分析伸缩缝与桥面铺装层的垂直界面接触条件对界面黏结状态影响时，主要是考虑不同摩擦系数的影响。

1.4 有限元模型

采用有限元法建立伸缩缝的二维平面应变模型，图3为受力分析简图(典型的伸缩缝尺寸为500 mm × 100 mm，钢板尺寸200 mm × 6 mm[7-8])，划分后二维模型网格如图4。

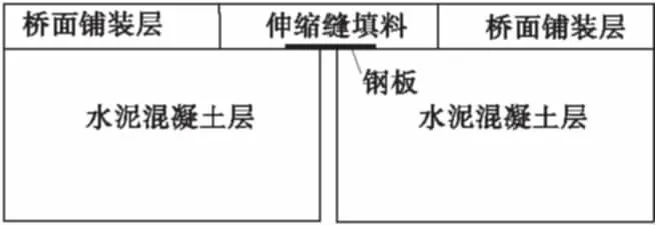
图3 连续式桥梁伸缩缝受力分析Fig.3 Force analysis diagram of continuous bridge expansion joints

图4 2D网格划分Fig.4 2D Meshing diagram

2 连续式桥梁伸缩缝界面受力分析

2.1 荷载作用下的伸缩缝界面受力分析

为了分析荷载作用下伸缩缝填料与桥面沥青铺装层界面的受力特征，考虑荷载在伸缩缝上3个不同位置，3个位置如图2。分别计算每个荷载位置下伸缩缝填料与桥面沥青铺装层界面的正应力Sx和剪应力Sxy分布情况，如图5。

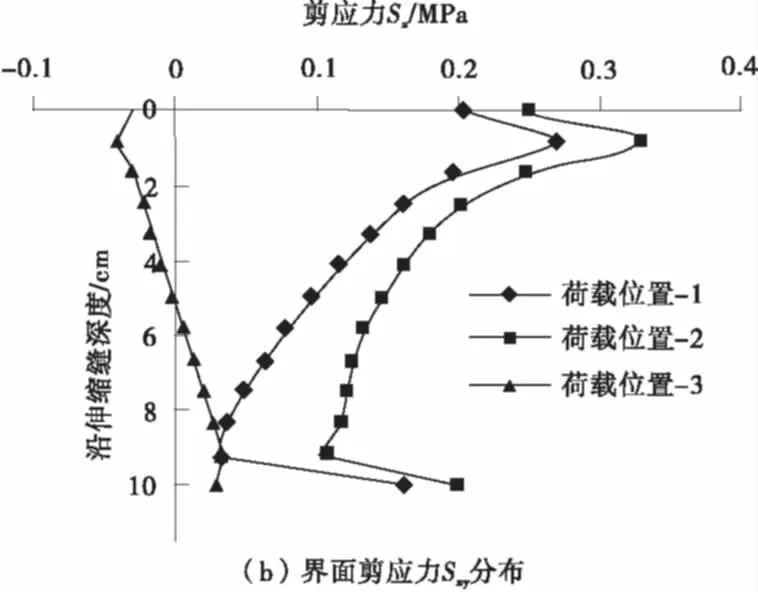
图5 荷载作用下界面正应力Sx及剪应力SXY分布Fig.5 Distribution of interfacial normal stress Sx and shear stress Sxy under traffic loads

从图5(a)可以看出：3个位置荷载作用下，沿伸缩缝深度方向，伸缩缝与桥面铺装层界面上大多数点受压应力作用，只有靠近表面的少许点受拉应力作用；此外，3种荷载位置中，当荷载作用在位置2时，沿着伸缩缝深度方向，界面上每一点的正应力Sx值都最大。

从图5(b)可以看出：3个位置荷载作用下，伸缩缝与桥面沥青铺装层的界面剪应力Sxy最大值都是出现在离伸缩缝表面0.8 cm左右处；此外，3种荷载位置中，当荷载作用在位置2时，沿着伸缩缝深度方向，界面上每一点的剪应力Sxy值都最大。

综上，3个荷载位置作用下，当荷载作用在位置2时，沿着伸缩缝深度方向，界面上每一点的剪应力Sxy值和正应力Sx值都比其他两个位置大很多，所以认为荷载位置2为最不利荷载作用位置；荷载作用下，剪应力Sxy比正应力Sx对界面受力状态的影响更大，所以将剪应力Sxy作为荷载作用下伸缩缝界面的主要力学分析指标；荷载作用下，剪应力Sxy最大值为0.33 MPa，认为剪应力值最大处为界面在荷载作用下最不利的位置，即距离伸缩缝表面0.8 cm左右的区域为界面在荷载作用下的最不利位置。

对于荷载作用下，界面剪应力值在伸缩缝层底区域有一定的突变，这主要可能是由于本模型比较简单，其中采用的水泥混凝土模量很大，而伸缩缝材料模量很小，在这两种模量相差很大的材料接触的地方未做相关处理引起的。

2.2 温度作用下的伸缩缝界面受力分析

为了分析温度收缩变形时伸缩缝和桥面沥青铺装层的界面受力特征，通过固定伸缩缝模型一边横向位移，对另一边施加3种不同初始水平位移Δ1= 5 mm，Δ2= 10 mm，Δ3= 15 mm(对于20 m长的桥梁，在-20～40 ℃下，其收缩位移为10 mm左右)，来模拟温度作用下伸缩缝的伸缩变形，建立的模型如图6。计算出温度作用下，伸缩缝填料与桥面沥青铺装层界面的拉应力Sx和剪应力Sxy分布情况如图7。

图6 水平位移Fig.6 Horizontal displacement diagram

图7 温度作用下界面拉应力Sx 及界面剪应力Sxy分布Fig.7 Distribution of interfacial tensile stress Sx and interfacial shear stress Sxy under temperature

从图7(a)可以看出：在3种初始温度位移作用下，随着施加的温度位移不断增大，界面拉应力Sx值也在不断增大；沿着伸缩缝深度方向，界面拉应力Sx值不断减小但是在层底区域发生突变，界面拉应力Sx最大值出现在伸缩缝界面顶点处。

由图7(b)可以看出：在3种初始温度位移作用下，随着施加的温度位移不断增大，伸缩缝与桥面沥青铺装层的界面剪应力Sxy值也在不断增大；沿着伸缩缝深度方向，界面剪应力值先减小再增大，峰值出现在伸缩缝界面顶点处。

综上，在温度作用下，界面拉应力Sx比起剪应力Sxy对界面受力状态的影响更大，所以将界面拉应力Sx作为温度作用下界面的主要力学分析指标；温度作用下，界面拉应力Sx最大值出现在伸缩缝界面顶点，认为拉应力出现峰值的位置是界面在温度作用下最不利的位置，即温度作用下，界面的最不利位置为伸缩缝界面顶点。

对于温度作用下，界面拉应力值在伸缩缝层底区域有一定的突变，这主要可能是由于本模型比较简单，其中采用的水泥混凝土模量很大，而伸缩缝材料模量很小，在这两种模量相差很大的材料接触的地方未做相关处理引起的。

2.3 连续式桥梁伸缩缝界面脱开原因分析

连续式桥梁伸缩缝界面主要受到荷载和温度收缩变形的反复作用。当荷载作用产生的界面剪应力值大于界面的黏结强度时，伸缩缝界面在荷载作用下的最不利位置即伸缩缝表面区域会先开裂，然后向下扩展，最后整个界面产生裂缝，在荷载的反复作用下，界面就会脱开。当温度收缩变形产生的界面拉应力值大于界面黏结强度时，伸缩缝界面在温缩作用下的最不利位置即伸缩缝界面顶点处，会先开裂然后向下扩展，最后整个界面产生裂缝，在温度收缩变形的反复作用下，界面就会脱开。通过力学计算结果分析发现，当温度收缩变形比较大时，由温度收缩变形产生的界面拉应力值要比荷载作用产生的剪应力值大；当温度收缩变形比较小时，由温度收缩变形产生的界面拉应力值要比荷载作用产生的剪应力值小。由于连续式桥梁伸缩缝只适用于中小跨径、温度收缩变形比较小的桥梁，所以造成伸缩缝界面脱开的主要因素是荷载的反复作用。

3 伸缩缝界面黏结性能影响因素

连续式伸缩缝界面的黏结性能影响因素有很多，笔者主要考虑伸缩缝的材料模量、伸缩缝的铺装厚度、宽度和界面接触条件等4个方面。

3.1 伸缩缝材料模量

伸缩缝所用的填料为弹塑性改性沥青混合料，由于其特殊的级配和油石比造成了该混合料的模量比较低，和两边的桥面沥青铺装材料模量相差很大，笔者假定在特定温度环境下，桥面铺装层模量不变(E2= 1 400 MPa)，通过改变弹塑性改性沥青混合料的模量，即通过不同的模量比λ(λ=伸缩缝材料模量E1/桥面铺装层模量E2)，来模拟分析伸缩缝界面在荷载和温度作用下相应力学指标的变化趋势，如图8。

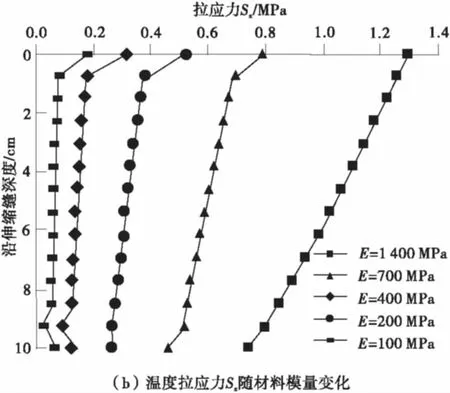
图8 荷载剪应力Sxy及温度拉应力Sx随材料模量变化曲线Fig.8 Curve of shear stress Sxy and tensile stress Sxchanging with material modulus

从图8(a)可以看出：在距离伸缩缝表面层一定深度范围内(5 cm左右)，随着伸缩缝材料模量的不断增大，沿着伸缩缝深度方向，界面上每一点的荷载剪应力Sxy值不断减小，剪应力Sxy峰值出现在离伸缩缝表面0.8 cm左右处；超过这个深度范围之外，随着伸缩缝材料模量的不断增大，沿着伸缩缝深度方向，界面上每一点的荷载剪应力Sxy值不断增大。

从图8(b)可以看出：随着伸缩缝材料模量的不断增大，沿着伸缩缝深度方向，界面上每一点的温度拉应力Sx值都不断增大，拉应力Sx峰值出现在伸缩缝界面顶点。

综上，去除模型本身的不足对结果的相关影响，笔者重点分析在界面拉应力和剪应力峰值区域，伸缩缝材料模量对界面的受力影响。由前面分析可知，界面剪应力和拉应力峰值区域为伸缩缝表面区域，在峰值区域，提高伸缩缝材料模量，可以降低界面荷载剪应力值，但是同时也会提高界面温度拉应力值； 由于界面荷载剪应力比起界面温度拉应力对界面的黏结状态影响更大，所以可以优先考虑降低荷载剪应力值，即可以适当提高伸缩缝材料模量值，来相应提高界面黏结性能。

3.2 伸缩缝铺装厚度

连续式桥梁伸缩缝的铺装厚度对伸缩缝界面在温度和荷载作用下的受力状态有一定的影响，因此有必要分析伸缩缝界面在不同铺装厚度下的受力变化情况，图9(a)，(b)分别为在荷载和温度作用下界面剪应力Sxy和拉应力Sx随伸缩缝厚度变化的趋势。

图9 荷载剪应力Sxy及温度拉应力Sx随伸缩缝厚度变化曲线Fig.9 Curve of shear stress Sxy and tensile stress Sxchanging with expansion joint thickness

从图9(a)可以看出：随着伸缩缝铺装厚度的增加，荷载作用产生的界面剪应力值不断增大；从图9(b)可以看出：随着伸缩缝铺装厚度的增加，温度作用产生的界面拉应力值也不断增大。

从图9可以发现：增加伸缩缝铺装厚度会提高界面剪应力和拉应力值，对界面黏结状态不利，所以应该限制伸缩缝铺装厚度，但是伸缩缝的铺装厚度同时受限于桥面铺装层厚度，所以要综合考虑这些方面的影响。

综上，随着伸缩缝铺装厚度的增加，界面剪应力值不断增大，可能是由于在相同的荷载作用下，增加伸缩缝厚度会增加伸缩缝的表面竖向变形，同样会增加伸缩缝界面的剪切变形，所以界面剪应力值随着铺装厚度的增加而增加；随着伸缩缝铺装厚度的增加，界面拉应力也不断增大，可能是随着铺装厚度的增加，伸缩缝界面的面积也在不断增大的缘故。

3.3 伸缩缝宽度

伸缩缝宽度一般是根据伸缩量大小来确定的，不同伸缩缝宽度对界面力状态的影响如图10。

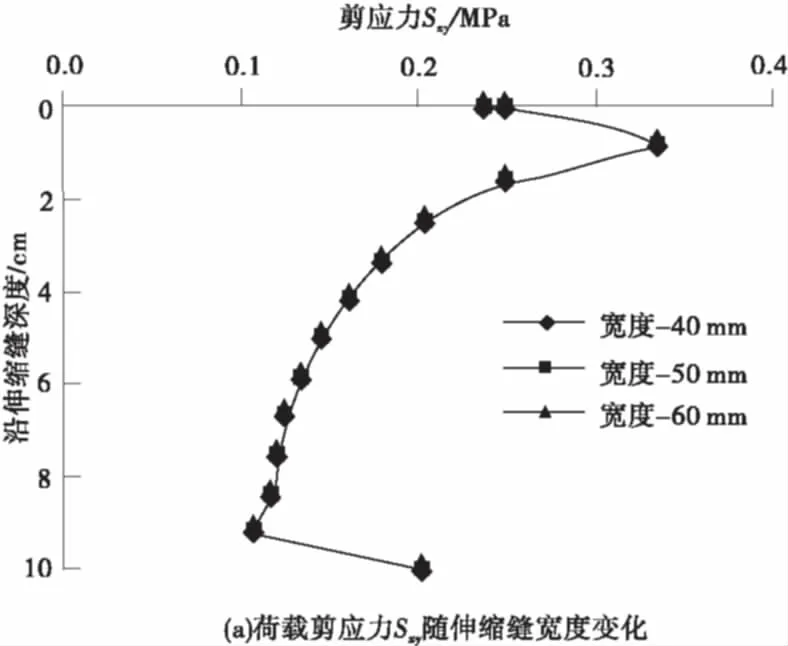
图10 荷载剪应力Sxy及温度拉应力Sx随伸缩缝宽度变化曲线Fig.10 Curve of shear stress Sxy and tensile stress Sx changing with expansion joint width

从图10(a)可以看出：随着伸缩缝宽度的增加，界面剪应力Sxy值基本不变；由图10(b)可以看出：随着伸缩缝宽度的增加，沿着伸缩缝深度方向，界面上每一点的拉应力值Sx不断减小。

综上，增加伸缩缝宽度，对界面剪应力值Sxy基本没影响，却可以减小界面拉应力Sxy值，所以适当增加伸缩缝宽度有利于伸缩缝的界面黏结性能。但是由于伸缩缝材料本身的特性，增加伸缩缝宽度也会增加伸缩缝的竖向位移，所以必须综合考虑确定一个合适的宽度既有利于界面黏结同时也能保证伸缩缝的竖向位移。

3.4 界面接触条件

伸缩缝与桥面铺装层的界面接触条件对界面受力特征的影响主要是摩擦系数的影响，如图11。

图11 荷载剪应力Sxy及界面切向位移与摩擦系数关系曲线Fig.11 Correlation curve among shear stress Sxy, interface tangential displacement and friction coefficient

从图11(a)中可以看出：随着界面摩擦系数的增加，沿着伸缩缝深度方向，界面上每一点的荷载剪应力Sxy值都在不断增大；由图11(b)中可以看出：随着界面摩擦系数的增加，沿着伸缩缝深度方向，界面上每一点的切向位移都在不断减小。

综上，增加界面摩擦系数，界面荷载剪应力会随之增加，但是界面各点的切向位移随之减小；当界面摩擦系数增加0.25，界面剪应力增加96%，界面切向位移减小35%，所以界面摩擦系数的变化对剪应力的影响更大，适当地减小摩擦系数可以减小界面剪应力。

4 结 论

1)伸缩缝界面同时受到荷载剪应力和温度拉应力的作用，当温度收缩变形比较大时，由温度收缩变形产生的界面拉应力值要比荷载作用产生的剪应力值大；当温度收缩变形比较小时，由温度收缩变形产生的界面拉应力值要比荷载作用产生的剪应力值小。

2)适当地提高伸缩缝材料模量，即适当地减小伸缩缝材料和桥面铺装层的模量差可以相应地提高伸缩缝界面的黏结性能；适当地增加伸缩缝宽度可以相应地提高伸缩缝界面的黏结性能；适当地减小伸缩缝铺装厚度有利于伸缩缝界面的黏结性能，但是伸缩缝铺装厚度同时受限于桥面铺装厚度；适当地减小界面摩擦系数可以减小界面剪应力，有利于伸缩缝界面黏结性能。

[1] 唐涛.弹塑性体改性沥青桥梁伸缩缝在寒冷地区应用技术的研究[D].哈尔滨:东北林业大学,2003.Tang Tao.Research on Technique of Modified Asphalt Bridge Expansion Joint Applied in Low Temperature Areas [D].Harbin: Northeast Forestry University,2003.

[2] Johnson I D,McAndrew S P.Research into the Condition and Performance of Bridge Deck Expansion Joints [R].Browthorne,Berkshire,England: Bridge Resource Centre, Transport Research Laboratory,1993.

[3] Park P,El-Tawil S,Park Sang-Yeol.Improved geometric design of bridge asphalt plug joints [J].Bridge Engineering,2011,16:158-165.

[4] Park P,El-Tawil S,Sang-Yeol P,et al.Behavior of bridge asphalt plug joints under thermal and traffic loads [J].Bridge Engineering,2010,5:250-259.

[5] Bramel B K,Dolan C W,Puckett J A,et al.Asphalt Plug Joints:Characterization and Specifications [D].Laramie,Wyoming: Department of Civil and Architectural Engineering,University of Wyoming,1999.

[6] CJJ 11—2011 城市桥梁设计规范[S].北京:中国建筑工业出版社, 2011.CJJ 11—2011 Code for Design of the Municipal Bridge [S].Beijing:China Building Industry Press,2011.

[7] ASTM D 6297-01 Standard Specification for Asphaltic Plug Joints for Bridges [S].Paris:West Conshohocken,2007.

[8] Bridge Joint Association.Standard for Asphaltic Plug Joints [S].Blackwater,Camberley,U.K.:Concrete Bridge Development Group,2003.