形状记忆合金辅助索-简化索网模型振动特性的数值模拟及试验研究

周海俊，陈朝骏，杨 夏，林焙淳

(深圳大学 广东省滨海土木工程耐久性重点实验室，广东 深圳 518060)

随着斜拉桥跨径的增大，斜拉索也变得越来越长，其具有长、柔、轻且阻尼小的特点将更为突出，在外界环境激励下极易产生各种振动。目前工程界控制拉索振动的方法主要有：索表面改变外形的气动措施、索端部安装阻尼器，及将拉索相互连接形成索网的辅助索措施[1]。对于辅助索措施而言，目前应用的多是钢绞线辅助索，但钢绞线辅助索在弹性阶段并不提供耗能能力，无法耗散振动能量。工程应用中也曾发生过由于拉索振动幅度过大而导致钢绞线辅助索的疲劳破坏事故[2]。形状记忆合金具有超弹性及良好的耐久性能，在土木工程结构减振方面具有广泛的应用前景。为了更好地了解SMA材料并有效的将其应用到拉索减振工程中，研究人员在研究SMA材料特性的同时，提出采用SMA作为斜拉桥的辅助索，并进行了初步的实验研究[3-4](图1)。笔者基于上述实验研究结果，采用有限元方法模拟分析了SMA辅助索-简化索网系统的自由振动响应，采用对数衰减率计算其模态阻尼比并与模型实验结果进行了对比分析。

图1 SMA辅助索-简化索网模型Fig.1 A simple cable net model with a SMA cross-tie

1 SMA辅助索-简化索网模型

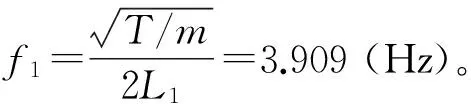
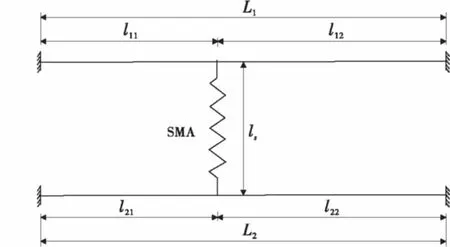
图2 SMA辅助索-简化索网模型Fig.2 Simplified cable nets with a SMA cross-tie

2 有限元模型及计算方法

2.1 有限元模型

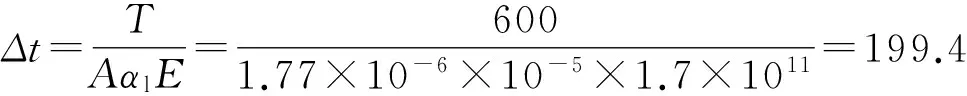
计算分析时，定义第1步为静力分析，第2步为模态分析(子空间迭代法)，第3步是瞬时动态分析，分析时长为200 s，时间增量为0.01 s。

2.2 ABAQUS内嵌的SMA本构模型

ABAQUS通用有限元软件中内嵌了SMA材料子程序本构模型，图3为SMA内嵌本构模型，其中相关参数含义见文献[6]。图4是笔者在前期测得的SMA材料的应力-应变曲线[3]。

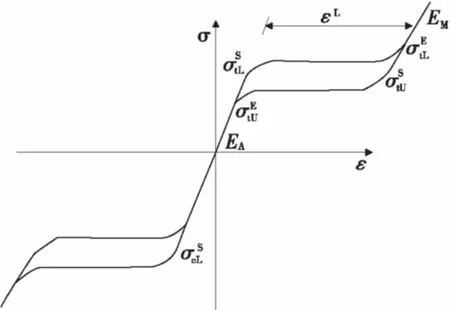
图3 SMA内嵌本构模型Fig.3 Embedded SMA constitutive models

图4 SMA材料本构模型Fig.4 SMA material constitutive model

根据上述SMA棒材超弹性拉伸试验，基于慢速(0.1 mm/min)下应变为3%和5%的试验循环数据的应力-应变关系，得到SMA的本构模型，拟合得到了SMA材料的基本属性参数如表1。

表1 ABAQUS内嵌的SMA辅助索本构模型参数值 Table 1 Parameters’ value for ABAQUS’s SMA constitutive model

2.3 与SMA辅助索对比的连接弹簧参数

由于普通钢丝自身并不能耗散能量，只提供轴向连接刚度，因此采用弹簧连接模拟普通钢丝制成的辅助索。为对比分析普通钢丝制成的辅助索与SMA辅助索的不同，同时分析了弹簧连接的简化索网模型的振动特性。

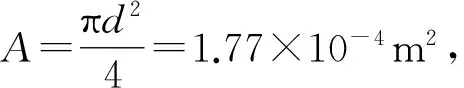
3 计算结果分析

3.1 简化索网模型振动特性

研究表明[7-8]，索网模型存在两类模态振动，这两类模态振动对应着单根拉索各阶次振动的同相位、反相位的模态振型；与同相位、反相位的模态振型相对应的则分别是较小、较大的振动频率。图5(a)、(b)分别为l11/L1=1/3时的同相位、反相位的SMA辅助索-简化索网系统的1阶振动模态。

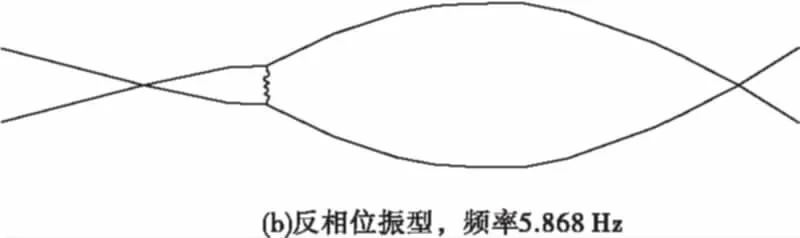
图5 索网模型同相位、反相位振动模态Fig.5 In-phase and out-phase vibration mode shape of cable nets

3.2 SMA辅助索与弹簧连接的比较

以辅助索的安装位置l11/L1=1/3时的同向振动模态工况为例，图6(a)为采用SMA辅助索时，距上索左端点3/4L1处简化索网位移时程衰减曲线；图6(b)为辅助索是弹簧时，距上索左端点3/4L1处简化索网的位移时程衰减曲线。可见，SMA辅助索的简化索网位移时程衰减明显快于弹簧连接简化索网的位移时程衰减。

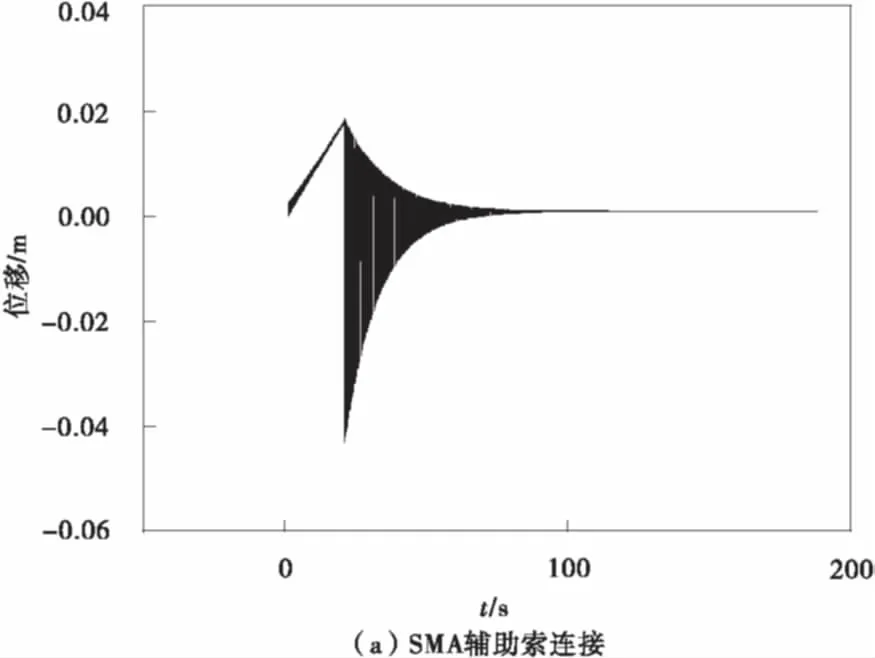
将位移时程曲线经FFT分析后，采用MATLAB对其进行滤波处理，得到目标频率和滤波后的位移时程曲线，由对数衰减法计算出索网模型的模态阻尼比：

(1)

式中：yk为k周期时对应的振动幅值；y(k+n)为(k+n)周期时对应的振动幅值。

计算结果表明：上述工况中SMA辅助索-简化索网系统的阻尼比为0.096 6%，弹簧连接-简化索网系统的模态阻尼比约为0.052 0%。说明SMA辅助索可有效的提高索网系统的模态阻尼。

由于拉索同相位振动时SMA辅助索的约束作用很小，而拉索不同相位振动时SMA辅助索约束作用较大，对频率影响较大；因此1阶同相位频率与单索振动频率较为接近，而1阶反相位频率会明显大于单索振动频率，具体则与SMA辅助索安装位置有关。

表2列出了改变SMA辅助索的安装位置时索网的1阶振动频率和阻尼比的变化。可知随着辅助索安装位置离中点距离越远，反相位频率越小，并且越接近同相位频率，而同相位频率则变化很小；随着辅助索安装位置离中点距离越远，模态阻尼比越小。

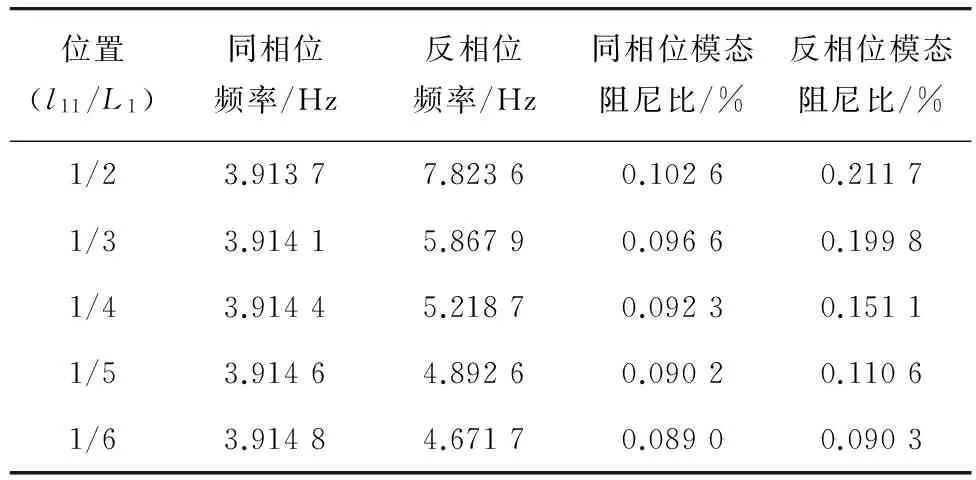
表2 索网模型的1阶振动频率、阻尼比 Table 2 The first mode vibration frequency and damping ratio of cable net model

4 数值模拟与实验结果的比较

为了验证模拟的正确性，笔者同时进行了模型实验研究。图7(a)为SMA辅助索-简化索网模型的1阶模态阻尼的数值模拟结果和试验结果的对比。可见，两者得到的模态阻尼比的变化趋势是比较相似的，都是随着辅助索安装位置离中点距离越近，模态阻尼比越大，也从侧面反应了数值模拟的准确性。数值模拟得到的SMA辅助索-简化索网模型的1阶频率与试验得到的结果进行比较，数据表明，数值模拟结果与试验结果是吻合的，如图7(b)。

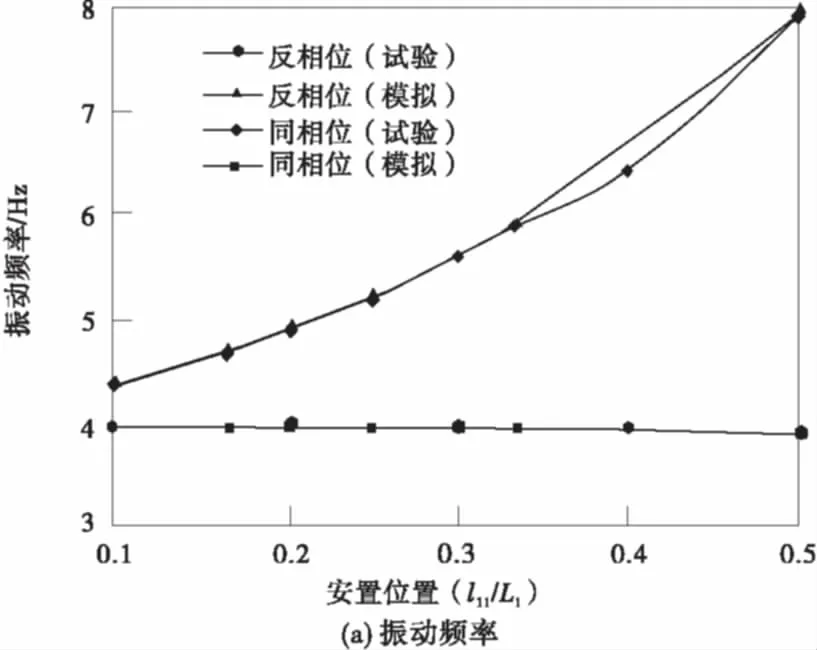
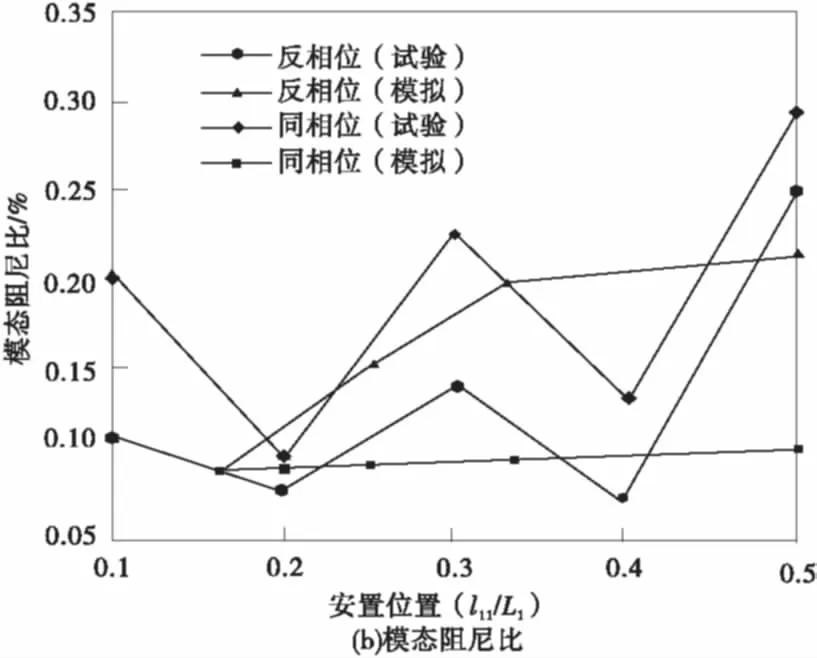
图7 数值模拟与试验结果比较Fig.7 Comparison of numerical simulation and experiment results

5 结 论

采用数值模拟和模型实验方法对SMA辅助索与普通钢丝连接的简化索网的阻尼和频率特性进行了初步的比较研究，对于索网结构的1阶振动模态，可得到以下结论。

1)由于拉索同相位振动时SMA辅助索的约束作用较小，而拉索不同相位振动时SMA辅助索约束效应较大，对频率影响较大。因此索网模型的1阶同相位振动频率与单索模型的1阶振动频率非常接近，而索网模型的1阶反相位振动频率会明显大于单索模型的1阶振动频率，具体则与SMA辅助索的设置位置有关，随着辅助索位置接近于索网模型的中点，索网模型的1阶反相位振动频率会越来越大，相对应的模态阻尼比也会增大。

2)对于索网模型的1阶反相位振动，SMA辅助索安装在索网中点时的模态阻尼比最高，且辅助索安装位置离中点距离越远，模态阻尼比越小。

3)由于SMA材料的超弹性耗能作用，其索网模型的模态阻尼比较普通钢丝要大。

[1] 周亚刚.斜拉索-辅助索系统动力特性和减振研究[D].上海:同济大学, 2007.Zhou Yagang.Dynamic Characteristics and Vibration Mitigation of Stay Cables Using Cross Ties [D].Shanghai:Tongji University,2007.

[2] Caracoglia L,Zuo Delong.Effective of cable networks of various configurations in suppressing stay-cable vibration [J].Engineering Structures,2009,31(12):2851-2864.

[3] 刘海峰.Ni-Ti形状记忆合金桥梁抗震防落装置研究[D].深圳:深圳大学,2011.Liu Haifeng.Study of Ni-Ti Shape Memory Alloy Bridge Restrainers for Unseating Problem [D].Shenzhen: Shenzhen University,2011.

[4] 丁炜.形状记忆合金辅助索-阻尼器-拉索的简化索网振动特性分析[D].深圳:深圳大学,2011.Ding Wei.Study of Dynamic Behaviors of Simple Cable Nets with Connected Shape Memory Alloy Cross-Tie and Attached Dampers [D].Shenzhen: Shenzhen University,2011.

[5] Clough R W,Penzien J.Dynamics of Structures [M]//Computers and Structures.2nded.New York:McGraw-Hiu,2003.

[6] Ferdinando A,Robert L,Lubliner T J.Shape-memory alloys:macro-modeling and numerical simulations of the super-elastic behavior [J].Computer Methods in Applied Mechanics and Engineering,1997,146:281-312.

[7] Caracoglia L,Jones N P.In-plane dynamic behavior of cable networks-Part 1: formulation and basic solutions [J].Journal of Sound and Vibration,2005,279(3/4/5):969-991.

[8] Zhou Haijun,Yang Xia.Free Vibration of a Simple Cable-Network-Damper System[C]//Proceedings of 12thInternational Symposium on Structural Engineering.Wuhan,China:Huazhong University of Science and Technology,2012:1480-1485.