基于单向流固耦合的叶轮强度和振动研究

杜子学，韩山河，刘雅黔，查 雷

(1. 重庆交通大学 机电与汽车工程学院，重庆 400074；2. 重庆德蚨乐机械制造有限公司，重庆401122)

0 引 言

在压气机整个通道中，叶轮是唯一对流体做功的部件，它将同轴连接的涡轮提供的机械能转化为流体的压力能和动能，所以在压气机正常工作时，叶轮的受力非常复杂，除了受离心力、气动力和热应力外，还受到振动交变负荷的影响。在离心压气机中，叶轮设计的好坏对压气机的性能起着决定性作用，但随着增压器压比和转速的不断提高，叶轮机械负荷增加，寿命要求更长，成本要求更低，这就使得以结构优化为目的的结构分析变得更为重要[1]。叶轮在流动的气流场中，流体对叶轮的工作性能产生一定的影响，结构的扰动反过来影响流场，从而形成一个流固耦合模型[2]。通过单向流固耦合分析，在一定程度上可得到更为准确的强度和振动数据，叶轮的强度分析的目的是计算叶轮在工作载荷下的变形、应力分布及最大应力的大小[3]，以验证叶轮结构是否可靠，为压气机的设计提供依据。模态分析是利用静力学的计算结果，计算出叶轮的固有频率，分析对比转速对叶轮固有频率的影响，并算出叶轮在常用工作转速下的共振转速，为预防事故发生、延长压气机使用寿命提供可靠的数据[4]。

笔者利用某增压器压气机半开式叶轮为研究对象，采用流体软件NUMECA和有限元软件ANSYS联合仿真，考虑流固耦合作用对叶轮的影响，对叶轮强度和振动进行研究分析。

1 流体计算模型

1.1 叶轮的主要结构特征与参数

1)压气机叶片为前倾后弯的结构，叶片数为20片，其中长叶片10片，短叶片10片；

2)叶顶间隙为0.5 mm；

3)扩压气叶片数为23片；

4)轮盘直径86 mm，轮盖直径210 mm，叶轮出口直径为310 mm。

1.2 几何处理及网格划分

首先在三维制图软件中，提取出压气机叶轮的主要型线，再到IGG模块中做铺设网格面等处理，利用专用网格生成器Autogrid 5来划分网格，采用结构化网格，这种网格的生成速度较快，根据叶轮的对称性，只取一个通道进行流场分析。总网格数为2 047 755，且两叶片排网格的正交性均>10，延展比均<1 000，网格的长宽比均<5，如图1，网格的质量良好，可用于模拟分析计算。

图1 单通道计算模型Fig.1 Single channel calculation model

1.3 流场计算参数设置

本次计算选择的压气机叶轮转速为28 500 r/min，进行流场模拟计算时，工质采用具有可压缩性的真实空气，数学模型选择Turbulent Navier-stokes，湍流模型选择Spalart-Allmaras，计算域的进口条件，假定轴向速度，切向速度与径向速度均为0，给定进口压力、温度和湍流黏度即可。出口边界采用质量流量出口，设置流量为4.6 m3/s。采用有限体积中心离散方法，空间项的离散采用中心差分格式，时间项采用4阶 Runge-Kutta方法迭代求解，并采用多重网格技术加速收敛[5]。

2 叶轮结构有限元模型

2.1 实体模型的建立和处理

ANSYS提供了4种创建模型的方法，即直接建模、实体建模、输入在计算机辅助设计系统中创建的实体模型和输入在计算机辅助设计系统中创建的有限元模型[6]，笔者在三维软件中创建好实体模型，通过Parasolid格式文件导入到ANSYS中计算。由于叶轮是典型的轴对称元件，不但几何形状轴对称，而且作用在它们上面的载荷和约束也是轴对称的，一般在计算中，将叶轮简化为空间轴对称结构来处理[7]，所以本分析在选取模型时，取出它的一个基本扇区，即叶轮的 1/10 来进行强度分析即可。在分割过程中，为了保证叶轮大小叶片的完整性，采用沿流道方向斜切的方法，其旋转周期为36°，叶轮沿周向有10个循环周期。循环对称分析和整体分析计算结果相差很小，而分析规模要小得多。为了提高单元网格的质量，在进行有限元分析之前，对几何结构进行清理，去除对结构影响较小的倒角。

2.2 参数设置与网格划分

叶轮为铝合金材料锻造生成，并进行了热处理和人工时效处理，材料密度ρ=2 800 kg/m3，泊松比υ=0.31，弹性模量Ε=71 000 N/mm2，屈服极限为350 MPa。由于叶轮形状比较复杂，采用4节点四面体等参单元，实体模型采用有限元网格自动划分，先划分粗网格，查看初步结果后对应力集中处再进行更精细的划分，这样可以得到较准确的计算结果。单扇区网格总数为85 357。绕z轴逆时针旋转，在叶轮的实际工作中，叶轮是不能延轴向移动的，所以对叶轮与轴的接触面进行全自由度约束(包括轴向、径向和切向方向)。施加载荷时设定叶轮的旋转转速ω=28 500 r/min，r表示半径，那么单元体积的离心力为：

(1)

3 流固耦合设置

流固耦合通常分为单向流固耦合和双向流固耦合，其中单向流固耦合，一般仅仅考虑流体对固体变形的影响，而忽略固体变形对流场的影响。双向耦合则在每一时刻都同时向对方发送相应的物理量。笔者采用单向流固耦合，其流程如图2，通过两个软件之间的接口，实现数据的传递和转换。最后把流场计算出来的气体作用力，添加到叶片的结构单元上。

图2 流固耦合方法Fig.2 The diagram of fluid-solid coupling method

图3为加载在结构网格上气体压力，即压气机内部流体所产生的作用在流固耦合界面(叶轮表面)上的力。

图3 气动载荷Fig.3 Aerodynamic load

4 叶轮的加载计算结果及分析

4.1 应力和应变计算结果

在通用后处理器里面查看结果，图4(a)为只考虑旋转载荷下叶轮变形，最大变形为0.247×10-3mm；图4(b)为旋转载荷及流体压力载荷共同作用下叶轮变形，最大变形为0.253×10-3mm。

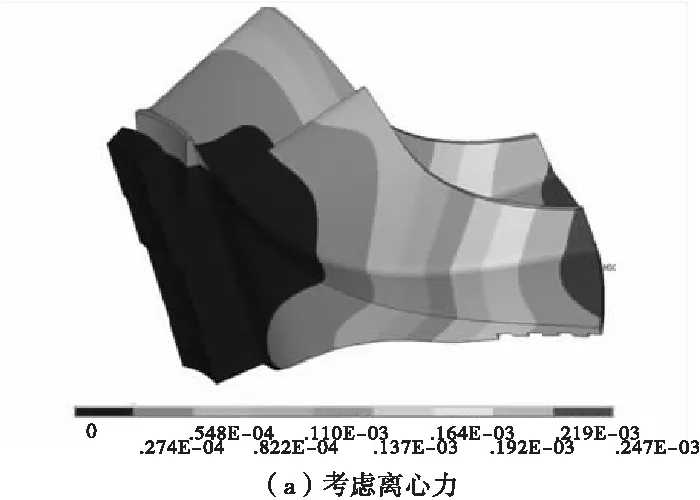
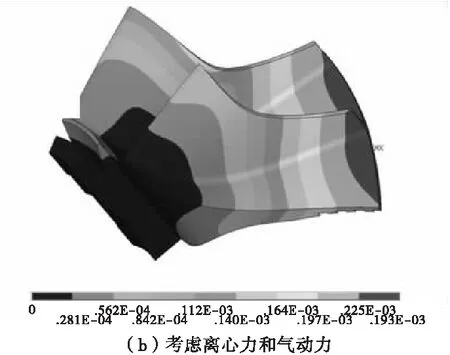
图4 叶轮的应变分布Fig.4 Strain distribution of the impeller

图5(a)为只考虑旋转载荷下叶轮应力，最大应力为278 MPa；图5(b)为旋转载荷及流体压力载荷共同作用下叶轮应力，最大应力为286 MPa。

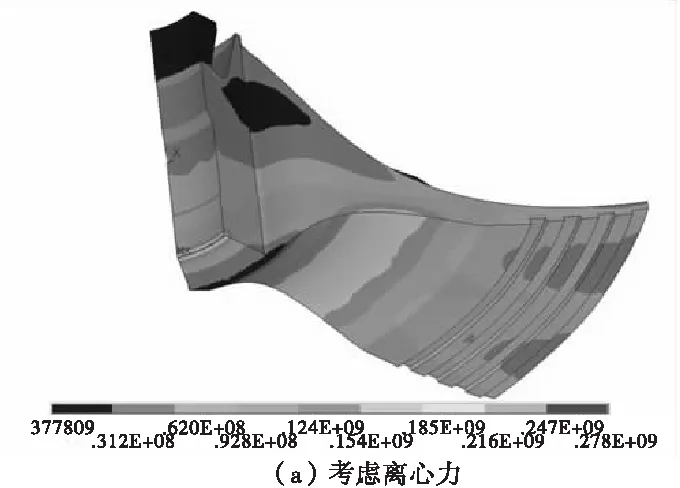
图5 叶轮应力分布Fig.5 Stress distribution of the impeller

4.2 结果分析

从图5可以看出，轴孔轮盘尾端区域和叶片根部存在较大应力集中，其中最大应力值出现在沿轴线方向上的轮盘尾端区域，这是由高速旋转的离心力在叶轮内部形成拉应力引起的，由叶轮的外形可以看出，叶轮底部材料比较多，质心靠近叶轮边缘一侧，惯性力比较大，因此，形成向外的离心力也比较大，牵动内部形成高应力区，上部正好相反 ，应力较小[8]。加载气动载荷后，应力有所增大，相对总应力而言，气动载荷对总应力的贡献不大。通过分析叶轮整体应力分布，可发现除部分位置应力值较大外，其余部位材料利用率偏低，应力值较小，可通过改变叶轮结构尺寸来提高材料利用率。叶轮的最大应力值为286 MPa ，而叶轮材料的屈服强度为350 MPa ，通过计算可知叶轮的安全系数为1.22，所以叶轮是偏于安全的。

5 模态分析

在静力学分析时选择预应力计算，在模态分析时选择Modal，模态的提取方法选择Block Lanczos法，该方法计算精度高，计算速度快。振型的数目选择为10，并计算预应力频率范围默认。分别对叶轮0，22 500，28 500 r/min等3组转速进行模态分析，得到相应的固有频率，如表1。

表1 不同转速下对应的前10阶频率

5.1 结果分析

由表1可知，压气机叶轮的固有频率随着转速的提高而相应增大，这是由于叶轮在高速旋转时所产生的离心力，使叶轮的弹性恢复力增加，从而使叶轮的各阶固有频率有所增加。且对低阶频率比高阶频率的影响更明显，其它28 500 r/min转速使叶轮的固有频率最大增大了1.62%，由此可知，转速对叶轮固有频率的影响整体不大。

5.2 叶轮共振分析

叶轮的Campbell图(图6)是判断叶轮在工作过程中是否发生共振的工程图解法[9]，它是三维图形的二维表达，图内斜线表示各种内部激振力。通过该图可以非常直观地看出叶轮在什么转速下发生共振，使叶轮在以后工作时远离共振点，为叶轮和叶片的优化设计提供依据。由于叶轮的常用工作转速为22 500 ～ 28 500 r/min，故只分析了该转速段的共振频率。从图6可知，叶轮的3阶固有频率与单倍的激振力作用下的频率相交于25 458 r/min，6阶固有频率与两倍的激振力作用下的频率相交于27 105 r/min。这说明，叶轮在以上两种转速下工作时容易发生共振现象。为了避免叶轮在工作时发生共振现象，应该调整固有频率或者激振频率。

图6 Campbell图Fig.6 Campbell diagram

6 结 论

1)对于增压器叶轮，轮毂轴孔区域应力最大；且叶轮的最大应力小于屈服应力，叶轮强度校核合格。

2)离心力对叶轮强度起着决定性的作用，是引起叶轮失效的最主要的原因，设计时应主要考虑减少叶轮的重量和旋转半径尺寸。

3) 叶轮的模态频率在考虑了预应力后，固有频率随转速的增加有所增加，但整体变化不大。

4)叶轮在常用工作转速段内共存在两个共振转速，为了避免产生共振现象，可以适当地改变叶轮叶片的结构，避免激振频率与固有频率相同或者相近。

[1] 王延生,黄佑生.车辆发动机废气涡轮增压器[M].北京:国防工业出版社,1984:142-143.

Wang Yansheng,Huang Yousheng.Exhaust Gas Turbo Charging of Vehicle Engine [M].Beijing:National Defense Industry Press,1984:142-143.

[2] 李惠彬,周鹂麟,孙恬恬,等.涡轮增压器叶轮流固耦合模态分析[J].振动、测试和诊断,2008,28(3):252-255.

Li Huibin,Zhou Lilin,Sun Tiantian,et al.Model analysis of turbocharger impeller considering fluid-soil interaction [J].Journal of Vibration,Measurement & Diagnosis,2008,28(3):252-255.

[3] Peng Guangjie,Wang Zhengwei.Strength analysis of a large centrifugal dredge pump case [J].Engineering Failure Analysis,2009,16(1):321-328.

[4] 骆清国,司东亚,冯建涛,等.基于流固耦合方法的离心式压气机叶片强度与振动特性研究[J].车用发动机,2012(2):51-54.

Luo Qingguo,Si Dongya,Feng Jiantao,et al.Strength and vibration characteristic analysis of centrifugal compressor impeller blade based on fluid-solid interaction method [J].Vehicle Engine,2012(2):51-54.

[5] 陈山,杨策,杨长茂,等.几何参数对离心叶轮强度和气动性能影响的研究[J].流体机械,2012,40(3):21-26,36.

Chen Shan,Yang Ce,Yang Changmao,et al.Investigation of geometrical parameters influence to the stress and aerodynamic performance of centrifugal impeller [J].Fluid Machinery,2012,40(3):21-26,36.

[6] 张朝晖.ANSYS8.0结构分析及实例解析[M].北京:机械工业出版社,2005:14-15.

Zhang Chaohui.Structure and Example Analysis Based on ANSYS 8.0 [M].Beijing:China Machine Press,2005:14-15.

[7] 张虹,马朝臣.车用涡轮增压器压气机叶轮强度计算与分析[J].内燃机工程,2007,27(1):62-66.

Zhang Hong,Ma Chaochen.Structure computation and analysis of vehicle turbocharger compressor impeller [J].Chinese Internal Combustion Engine Engineering,2007,27(1):62-66.

[8] 黄若,孟令广,张虹.增压器压气机叶轮低周疲劳强度有限元计算分析[J].内燃机工程,2006,27(4):55-57.

Huang Ruo,Meng Lingguang,Zhang Hong.LCF strength calculating and analyzing of turbocharger compressor wheel [J].Chinese Internal Combustion Engine Engineering,2006,27(4):55-57.

[9] 黄新忠,赵俊生.基本ANSYS的压气机叶轮振动特性有限元仿真分析[J].机械设计与制造,2012(2):12-14.

Huang Xinzhong,Zhao Junsheng.Vibration characteristic simulation and analysis of compressor impeller based on finite element [J]. Machinery Design & Manufacture,2012(2):12-14.