形心轴附加弯矩对四周布筋混凝土墩柱整体受力的分析

王 军，刘少乾，苏文明，郑 罡

(1.重庆交通大学 土木建筑学院，重庆400074；2.招商局重庆交通科研设计院有限公司，重庆 400067)

0 引 言

地震是人类面临最严重的自然灾害之一。纵观20世纪70年代以来世界各地多次大地震对桥梁造成的破坏情况，可以清楚地发现，很大一部分桥梁的破坏都与桥墩的破坏有关，如：墩顶位移预计不足而导致的落梁以及墩身、墩底结点位置开裂。所以，桥墩在地震作用下的性能是桥梁结构抗震研究的重要内容之一。

在实际工程中对于常见的单柱式桥墩在地震力作用下的性能分析，目前，学术上常采用的受力简化模式是[1-4]：墩顶受到来自于桥梁上部结构自身重量所产生的轴压力N以及由于地震作用引起的墩顶水平惯性力F的共同作用，且忽略墩身的质量、地震竖向惯性力以及墩顶位移引起的P-Δ效应，同时墩身各截面的弯矩沿墩高呈直线分布，如图1。

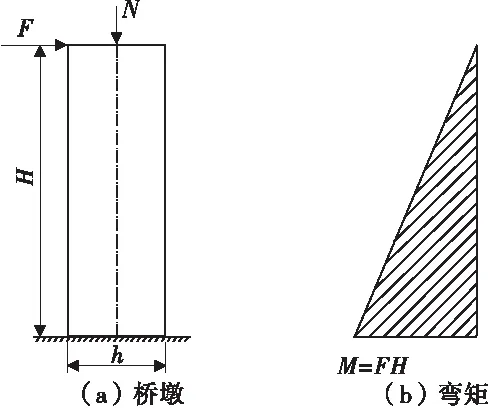
图1 桥墩受力示意Fig.1 Force diagram of bridge pier

由于混凝土材料的抗拉强度较小且其在受力过程中主要承受压力，因此在实际工程中，对于常见的钢筋混凝土桥墩，当其受到由地震作用产生的水平力作用时，在靠近墩以及墩身的部分截面，由于受拉区内的拉应力大于混凝土的抗拉强度而产生开裂，导致截面不再是开裂前的完整截面，开裂截面的中性轴和形心轴都将向受压区发生偏移、截面有效抗弯刚度减小。此时，对于墩身开裂截面，作用于墩顶的轴向压力N不再是位于截面形心轴上，而仍是位于截面开裂前的形心轴上，故轴向压力N会对开裂截面产生偏心受压的影响，并对开裂截面产生附加弯矩作用，该弯矩称之为形心轴附加弯矩。

1 模型简化

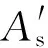
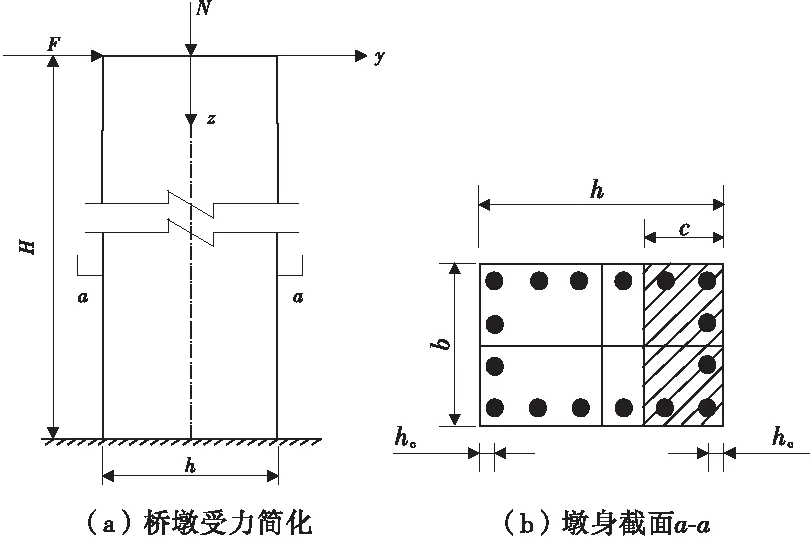
图2 钢筋混凝土墩柱受力形式示意Fig.2 Force diagram of reinforced concrete pier

对于常见的钢筋混凝土构件，在弹性范围内可做以下3个基本假定[6]：

1)平截面假定，即受弯之前的正截面在受弯后仍保持为平面，同时忽略剪切变形与滑移变形；

2)混凝土的抗拉强度为0，即混凝土受拉后立即开裂；

3)钢筋与混凝土均为理想的线弹性材料。

为了便于推导、分析，根据变换截面法[7]，可将构件中截面的钢筋换算成与混凝土弹性模量相同的变换截面，且在推导过程中忽略混凝土保护层厚度的影响。于是，四周布筋混凝土墩柱截面的受力情况可简化如图3，图中：εt表示截面受拉钢筋边缘的拉应变；εp表示截面受压钢筋和混凝土边缘的压应变；Nst表示受拉钢筋的拉力；Nsp、Ncp表示受压区钢筋与混凝土的压力；e表示水平力作用前、后形心轴偏移的距离。

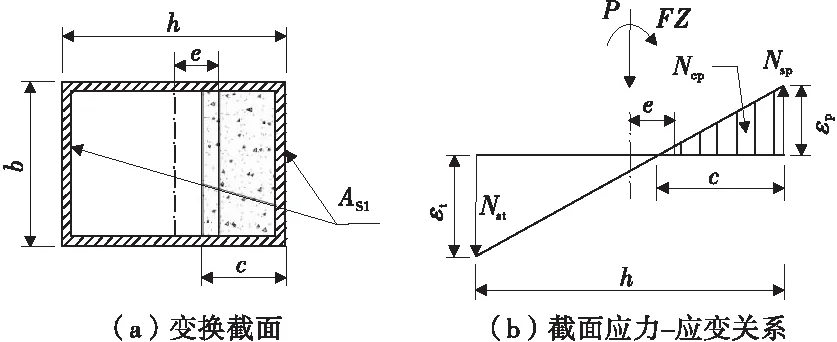
图3 开裂截面受力示意Fig.3 Force diagram of the cracking section

当墩顶只有轴向力N作用时，此时墩身的各个截面都处于全截面受压状态，且墩身所有截面的形心轴都与截面的几何中心轴重合。当墩顶同时有轴向力N和水平力F作用时，靠近墩底区域的部分截面将在受拉区边缘出现拉应力，根据第2)条假定，墩底的部分截面一旦出现拉应力，截面内的混凝土即开裂，截面开裂后受拉区的拉应力完全有受拉钢筋承担，墩身截面开裂后，开裂截面的形心轴、中性轴将同时向受压区偏移。

2 理论推导

形心轴附加弯矩是由于靠近墩底区域的部分截面开裂、形心轴向受压区偏移引起的。为此，在分析形心轴附加弯矩对墩柱受力和整体刚度的影响之前，先对形心轴偏移情况进行分析。

2.1 开裂截面形心轴偏移分析

对于简化后的混凝土墩柱构件，任取墩身截面进行分析，当墩顶只有轴向力N作用时，截面处于全截面受压状态，由截面形心轴两边的静矩相等可知其形心轴位于截面的几何中心轴上，如图4(a)；当墩顶在轴向力N与水平力F共同作用时，靠近墩底区域的部分截面受拉后开裂，此时截面的形心轴向受压区偏移，如图4(b)。

图4 截面形心轴偏移示意Fig.4 Diagram of deviation of center axis at the cross-section

2.2 截面平衡方程

根据图3的截面示意以及力学理论，截面受拉钢筋的拉力Nst、受压钢筋的压力Nsp、受压混凝土的压力Ncp的表达式如式(1)：

(1)

截面的平衡方程如式(2)：

(2)

截面的变形协调方程如式(3)：

(3)

2.3 形心轴沿墩高方向分布

根据式(2)可推导出忽略混凝土保护层厚度时截面的受压区高度与墩高的关系方程，如式(4)：

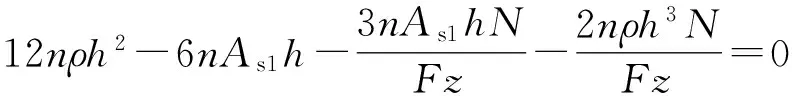
(4)

整理后可得：

(5)

对于式(5)，当c=h时，可求得全截面受压沿墩高的高度z0，即：

(6)

对于给定参数的四周布筋混凝土墩柱，在墩顶水平力F与轴压力N共同作用下，墩柱中性轴沿墩高分布如图5。

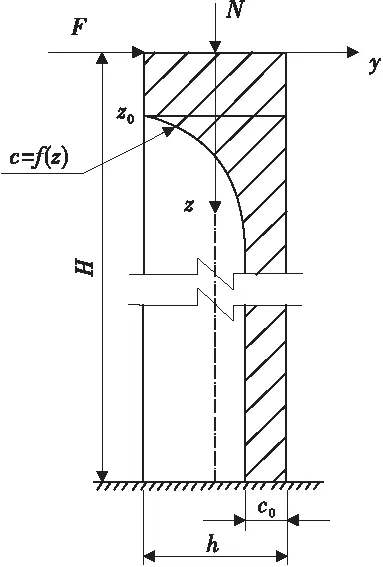
图5 截面受压区高度沿墩高分布示意Fig.5 Diagram of the cross-section force distributing along with the pier

对于墩身任一开裂截面，运用截面形心轴两侧的面积矩相等的原理，可求得偏心距与受压区高度存在如式(7)关系：

(7)

式(7)关于c求导并简化后得：

(8)

当墩顶在轴向力N与水平力F共同作用时，根据图3中e和c的关系有：

(9)

将式(7)带入式(9)得：

(As1+2ρh)(h-2c)-bc2<0

(10)

将式(10)带入式(8)可知e′<0，即函数e是关于变量c的单调减函数。

当墩高趋于无穷大或水平力很大时，式(4)可化简为：

bc2+(2As1+4ρh)nc-nAs1h-2nρh2=0

(11)

此时，墩底截面受压区高度趋于最小值c0，即：

c0=

(12)

将式(12)带入式(7)可得墩底截面形心轴偏移距离为：

(13)

根据图3，墩底截面偏心距e0与受压区高度c0的关系为：

(14)

将e0，c0带入式(14)可得：

d≠0

由分析过程可知，当墩高很高或水平力很大时，墩底截面的形心轴与中性轴位于同一位置；对于墩身开裂截面以上的未开裂截面，其截面的形心轴与截面的几何中心线位于同一位置。因此，由式(7)的单调关系以及墩底截面、墩身开裂与未开裂两个边界条件可以画出桥墩在水平力F与轴压力N共同作用时墩柱开裂区形心轴沿墩高的分布曲线，如图6中的e=f(c)曲线。此时，开裂截面由于偏心距的存在，轴压力与开裂截面的偏心距产生附加弯矩，该附加弯矩对整个墩柱的受力和变形都会产生一定的影响。

图6 形心轴沿墩高分布及弯矩示意Fig.6 Diagram of center axis distributing along with the pier and bending moment

3 外力弯矩沿墩高方向分布

对于钢筋混凝土墩柱构件，当墩顶受到轴压力N和水平力F共同作用时，轴压力N和水平力F均会对墩柱产生弯矩[8]影响。

对于墩顶水平集中力F，其引起的弯矩为MFi=Fzi，MFi沿墩高呈线性分布， 如图6。对于墩顶轴压力N，其引起的弯矩为MNi=Nei，由于开裂截面的形心轴沿墩高呈曲线分布及轴向压力N为常量，故MNi沿墩高呈曲线分布，由式(13)可知，墩底截面由轴向压力N引起的附加弯矩近似为一常量Ne0，且形心轴附加弯矩的方向与集中力F引起的弯矩方向相反，具体曲线分布如图6。

作用于混凝土墩顶的水平力F大小不同时，墩身的开裂程度不同，开裂截面的中性轴和受压区高度分布也不同。不同大小的水平力F作用下，墩柱的开裂以及总体弯矩分布情况是不同的,在水平力为F1

图7 不同大小水平力作用下墩柱开裂及弯矩分布示意Fig.7 Diagram of the pier cracking and bending moment with different horizontal forces

从图7可知，四周布筋的混凝土桥墩所受外力弯矩M随着墩顶水平力的增加而增大，且在墩身截面开裂区段显曲线分布。形心轴附加弯矩在一定程度上能够抑制墩身的变形。

4 形心轴附加弯矩对桥墩整体刚度影响

为使得分析结果简单明了，该部分以一个具体的四周布筋的矩形混凝土桥墩为例，对其截面刚度特性以及桥墩的整体刚度进行分析。桥墩受力模式简化后如图2，其中，墩高H=12 m，截面宽度b=1.5 m、高度h=2.0 m，经截面换算后的纵向钢筋总面积As=0.3 m2，截面上下(沿截面高度方向)两侧钢筋的变换面积As1=0.13 m2，截面左右(沿截面宽度方向)两侧钢筋的变换面积As2=0.17 m2、钢筋的宽度ρ=0.043 m，钢筋四周对称布置，轴压比μ=0.2，材料采用C30混凝土，其抗压强度设计值fcd=13.8 MPa，弹性模量Ec=3×104MPa；纵向钢筋采用HRB335钢筋，弹性模量Es=2×105MPa。为便于计算分析，水平力的加载模式采用集中力单向加载，墩顶水平力F由0逐渐增加的过程中，当墩底截面纵向边缘受拉钢筋应变εt=0.002时即发生屈服，以钢筋屈服为界，分析其在屈服前的受力特性及截面刚度、整体刚度的变化情况。

经计算，当墩底纵向受拉钢筋的应变εt=0.002时，墩柱开裂截面的受压区高度的分布曲线以及截面形心轴沿墩高的分布曲线如图8，墩柱在不考虑P-Δ效应的情况下总弯矩分布如图8。

图8 桥墩开裂及弯矩分布Fig.8 Diagram of the pier cracking and bending moment

在分析该混凝土墩柱的整体刚度之前，先对墩柱的变形进行分析，当不考虑形心轴附加弯矩的情况下计算出墩顶的位移；当考虑形心轴附加弯矩影响时计算出墩顶位移，得到如图9的水平力-位移曲线。

图9 桥墩墩顶水平力-位移曲线Fig.9 Diagram of force-displacement curve of the horizontal force at the top of bridge pier

由图9可知，在墩顶最大水平力作用下，不考虑形心轴附加弯矩情况下的墩顶位移明显大于考虑形心轴附加弯矩情况下的墩顶位移，这说明混凝土墩柱此时有一定的位移储备。换句话说，在墩顶承受相同的位移时，考虑形心轴附加弯矩比不考虑形心轴附加弯矩能承受更大的水平力。经计算，考虑形心轴附加弯矩的墩顶位移与不考虑形心轴附加弯矩时的墩顶位移之差约占不考虑形心轴附加弯矩情况下墩顶位移的20%。图9曲线上任意一点的割线斜率即为该墩的整体刚度，将两种情况下的割线斜率绘制成如图10的墩柱整体刚度变化曲线。

图10 桥墩归一化割线刚度变化Fig.10 Diagram of normalization secant stiffness of the bridge pier

从图10中可以看出，当桥墩有水平力F与轴压力N共同作用时，混凝土墩柱由于墩身的截面开裂而使混凝土墩柱的整体刚度明显下降，且当考虑形心轴附加弯矩时，混凝土墩柱整体刚度的退化比不考虑形心轴附加弯矩时要缓一些，即形心轴附加弯矩具有减缓混凝土墩柱整体刚度退化以及抑制截面开裂作用。

5 结 论

四周布筋混凝土墩柱在墩顶水平力和轴压力的共同作用下靠近墩底区域的部分截面开裂，轴向力引起的形心轴附加弯矩对混凝土墩柱的受力和变形都有一定的影响。通过理论分析、推导及具体实例的计算，得到如下结论：

1)当计入形心轴附加弯矩对墩柱的影响时，墩柱的总弯矩在靠近墩底的截面开裂区域呈曲线分布，而不再是直线分布。

2)形心轴附加弯矩具有减缓混凝土墩柱整体刚度退化以及抑制截面开裂作用，与不考虑形心轴附加弯矩影响的混凝土墩柱相比，考虑形心轴附加弯矩可使四周布筋的混凝土墩柱构件承受更大的水平力。

3)在水平推力一定的条件下，考虑形心轴附加弯矩时的墩顶位移小于不考虑形心轴附加弯矩时的位移，说明混凝土墩柱此时有一定的位移储备。因此，建议在相关的抗震研究分析中考虑形心轴附加弯矩对墩柱变形的影响。

[1] 李国豪.桥梁结构稳定与振动[M].北京:中国铁道出版社,2003.

Li Guohao.Stability and Vibration of Bridge Structure [M].Beijing:China Railway Publishing House,2003.

[2] 叶见曙.结构设计原理[M].北京:人民交通出版社,2000.

Ye Jianshu.Structure Design Principle [M].Beijing:China Communications Press,2000.

[3] Berry M P,Eberhard M O.Performance Modeling Strategies for Modern Reinforced Concrete Bridge Columns [R].California:University of California-Berkeley,2008.

[4] Lehman D E,Moehle J P.Seismic Performance of Well-Confined Concrete Bridge Columns [R].California:University of California-Berkeley,2007.

[5] 高波,苗宇,李贵乾,等.形心轴附加弯矩对墩柱整体受力的初步分析[J].世界地震工程,2011,27(2):129-134.

Gao Bo,Miao Yu,Li Guiqian,et al.Primary analysis on the effect of the additional moment of center axis on the whole mechanical behavior of a column [J].World Earthquake Engineering,2011,27(2):129-134.

[6] R.帕克,T.波利.钢筋混凝土结构[M].秦文钺,译.重庆:重庆大学出版社,1986.

Park R,Boli T.Reinforced Concrete Structure [M].Qin Wenyue,translation.Chongqing: Chongqing University Press,1986.

[7] S.P.铁摩辛柯,J.M.格尔.材料力学[M].李春亮,译.台北:晓园出版社,1985.

Timoshenko S P,Geer J M.Mechanics of Materials [M].Li Chunliang,translation.Taibei:Xiaoyuan Press,1985.

[8] 樊友景,李乐,李大望.压弯构件的附加弯矩分析[J].郑州大学学报:理学版,2007,39(3):183-186.

Fan Youjing,Li Le,Li Dawang.Analysis of the additional moment of beam-columns [J].Journal of Zhengzhou University:Natural Science,2007,39(3):183-186.