惯性导航平台橡胶减振器斜角布置方法＊

周亚东， 雷宏杰， 董萼良， 吴邵庆， 韩晓林， 费庆国

（1.东南大学工程力学系 南京，210096） （2.东南大学江苏省工程力学分析重点实验室 南京，210096）（3.中航工业西安飞行自动控制研究所 西安，710065）

引 言

惯性平台是平台式惯性导航系统的核心部件。随着现代科学技术的发展，现代军事技术对导弹、火箭等飞行器制导精度的要求不断提高，而作为惯性坐标基准和惯性测量装置的惯性平台，其静动态力学性能直接影响着惯性仪表的工作精度，进而影响飞行器的飞行精度［1］。由于导弹、火箭等飞行器所处的动力学环境往往具有宽频带、随机激励的特性，传统的橡胶隔振器在共振点上的传递率经常超出载机惯性导航系统所能接受的技术指标［2］，所以开发适用于复杂动力学环境的新型橡胶减振器并优化减振器的布置方式是惯导系统隔振设计的迫切任务。

惯导平台减振器安装在载机上，必然要求处理好减振系统固有频率、振动载荷或振动环境的激励频率，以及载机支承结构主要弹性频率三者之间的关系。理想状况下三者之间不存在振动耦合关系，工程实践中要求减振系统的固有频率尽量避开振动环境的激励频率。为了缩减平台系统的共振带宽，抑制系统角偏移，笔者以三向等刚度为技术目标，研究橡胶减振器的布置方式对于改变系统振动特性的效果。

1 三向等刚度

由于飞行器航向姿态的变化以及振动激励的多向性，飞行器振动环境在垂向与侧向有大致相等的振动量级，因而航空减振器必须具备两向乃至三向的承载与减振能力［3］。此外，军用飞机各种急剧机动动作以及加力、减速过程中都会产生相当大的惯性载荷与振动，更要求减振器具备三向承载、三向减振的能力。

用于惯导平台的减振系统同样必须具备多向性，并且为了进一步抑制振动干扰产生的测量误差，实现高精度导航，要求减振系统尽可能具备三向等刚度特性［4］。一方面，在减振系统三向等刚度时，若平台台体质量分布对称，则理论上系统的3个线振动固有频率与3个角振动固有频率分别相等，即平台的共振频率减少至2个，这大大减小了系统发生共振的几率，并且由经典隔振理论，阻尼在不同频率比下其隔振作用迥然不同，系统固有频率数量的减少为合理配置隔振橡胶的阻尼系数提供了方便；另一方面，惯导平台的角偏移是影响系统测量精度的最不利因素之一，当减振系统具备三向等刚度时，经过弹性中心的任何一坐标轴均为弹性主轴。外力沿弹性主轴作用时，系统的变形与作用力方向一致，角偏移得到了最大程度的抑制，所以平台减振系统的三向等刚度具有重要意义。

2 斜角布置方法

惯导平台的刚度远大于橡胶减振器支座，在分析其动力学特性时可以将其视为6自由度刚体，其振动自由度包含3个方向线振动与3个方向角振动。减振器布置的首要目标是使振动解耦。在减振系统设计中应尽可能解除平台6自由度之间的振动耦合，一方面便于减小可能激起共振响应的频带宽度，另一方面便于合理配置其固有频率，使激励频率远离共振频率，以获得良好的整体隔振效果［5］。

可以证明［6］，对于弹性支承上微幅振动的6自由度刚体，若弹性隔振元件的弹性中心与刚体质心重合，弹性主轴与惯性主轴重合，则振动微分方程的各系数矩阵成为对角阵，系统在物理上实现解耦。在实际应用中若使隔振器和被隔振对象的安装具有3个对称面，则满足结论要求，6自由度方程解耦。文献［7－9］研究了惯导平台减振器不同布置模式对角振动与线振动耦合程度的影响，分析得出8个橡胶减振器上下对称布置是一种相对理想的隔振模式。在平台台体质量分布对称时，系统存在3个对称面，理论上满足振动解耦的条件。但是由于橡胶材料的弹性模量一般是剪切模量的3倍左右，所以拉压方向刚度与剪切方向刚度相差很大，系统一般不满足三向等刚度特性。尽管可以通过结构优化等设计方法改变减振橡胶内部的几何尺寸、形状与拓扑形式，使得减振器轴向刚度与径向刚度趋于相等［10］，或者基于灵敏度技术进行减振器位置参数优化［11］，但这必然要延长设计周期，增加制造工艺上的复杂度，工程实用性不佳。

笔者提出一种三向等刚度型橡胶减振器布置方法，通过改变减振器的布置方式，使系统3个方向刚度近似相等，从而实现平台系统的三向等固有频率，缩减共振带宽，抑制角偏移。设在平台质心建立直角坐标系，坐标轴构成的平面为其对称面，斜角布置方法是将8个减振器分别在平台的顶部倾斜对称布置，使其轴向与各坐标轴的方向余弦相等。图1为传统布置方式与斜角布置方式的平面示意图。

采用新的布置方法后，一方面平台系统仍具有3个对称面，满足振动解耦条件；另一方面由于对称性，平台在三向分别发生单位位移时，橡胶受拉压部分与受剪切部分的比例基本不变，系统满足三向等刚度要求。此外，斜角布置与传统布置方式相比，拉大了部分减振器的距离，从而增加了系统的部分扭转刚度，这有利于提高系统角振动固有频率，减小发生角共振的几率。

图1 两种布置方式平面示意图Fig.1 Plan sketches of two placement methods

3 数值仿真

本节通过建立两种减振器布置方式的有限元模型，分析二者的动力学特性及动响应。对惯导平台和橡胶减振器作简化，平台台体用镂空铝块模拟，橡胶减振器高为30mm，底部直径为50mm，模型所使用的材料物理参数如表1所示，两种布置方式的有限元模型如图2所示。为叙述方便，分别记传统方式、斜角方式的模型为A和B。有限元模型采用四面体单元划分，其中：模型A单元总数为158 444，节点总数为32 276；模型B单元总数为153 876，节点总数为31 748。A和B模型的边界条件均为在减振橡胶底部固支。

表1 模型材料物理参数Tab.1 Physical parameters of materials

图2 两种布置方式的有限元模型Fig.2 Finite element models of two placement methods

3.1 正则模态分析

对两种布置方式的平台减振系统进行正则模态分析，各自的前6阶模态振型与固有频率计算结果分别列于图3、图4和表2。

表2 两种布置方式系统的固有频率Tab.2 Natural frequencies of two placement methods

由计算结果可以得出，改进布置方式后系统前3阶模态振型均为转动且固有频率基本一致，后3阶为平动模态，固有频率也大体相同。与传统布置方式相比，系统表现出了明显的三向等固有频率即三向等刚度特性。

3.2 随机振动分析

为了检验改进布置方式的减振效果，下面对两种有限元模型依次进行频率响应分析和随机振动分析。由模态分析结果可知，系统的固有频率主要集中在200Hz以下，因此设置扫频范围为0～200Hz，激励力幅值为1N，施加在台体底部一节点上。为了表征平台真实服役环境所受激励的非对称性，设置激励力与3个坐标轴均不平行。提取台体边缘一点的加速度响应，两个模型的加速度频响函数曲线如图5所示。可以看出，改进布置方式的共振峰个数明显小于改进之前，共振带宽被缩减在较窄范围内，达到了预期效果。

图3 传统布置方式模态振型Fig.3 The mode shapes of traditional placement method

惯导平台所处力学环境往往为高能量随机激励，隔离随机振动的主要目的是抑制隔振对象的随机振动强度，因而采用隔振对象的随机动响应均方根值作为品质指标。图6为两个模型随机激励力的功率谱密度（power spectral density，简称 PSD），图7为两个模型中平台台体同一位置的加速度响应PSD。在5～200Hz内计算得到改进前的加速度均方根值为13.70m／s2，改进后为9.78m／s2，即随机振动量级降低了30.09%。

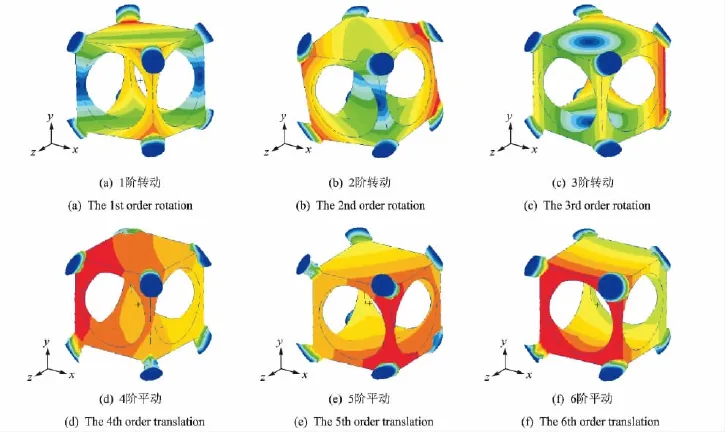
图4 4斜角布置方式模态振型Fig.4 The mode shapes of inclined placement method

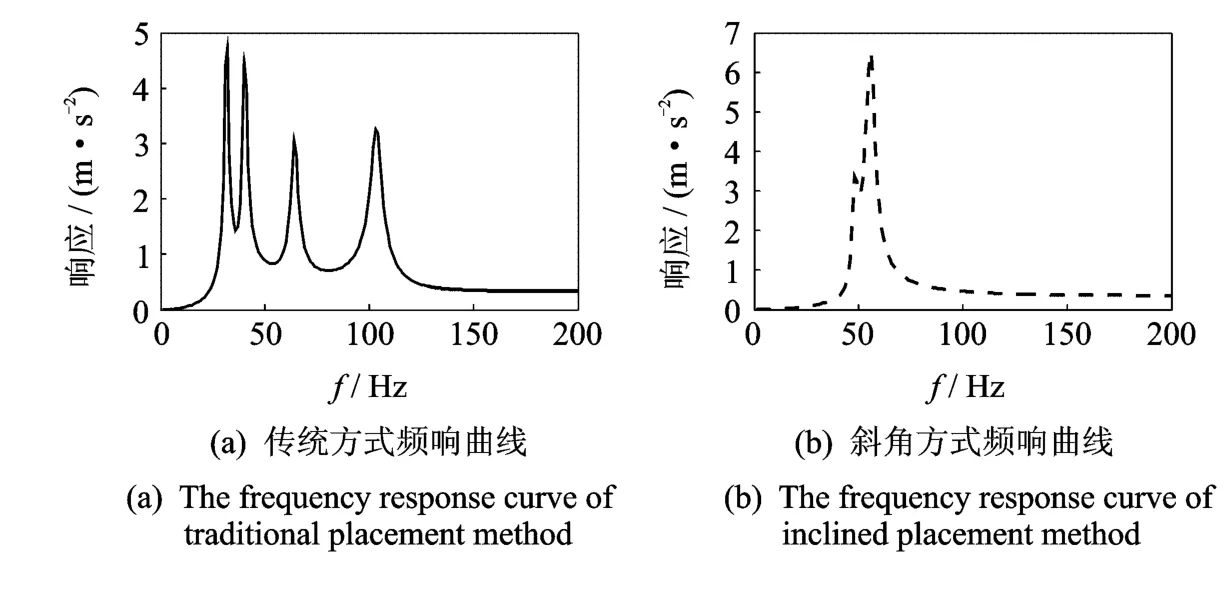
图5 加速度频率响应曲线Fig.5 The frequency response curve of acceleration

图6 输入功率谱密度Fig.6 The input PSD

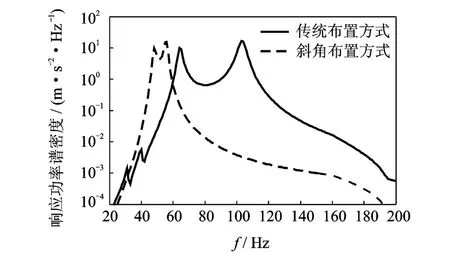
图7 加速度响应功率谱密度Fig.7 The PSD of acceleration response

4 结 论

1）传统的惯导平台橡胶减振器上下面对称布置的安装方式满足振动解耦的条件，角振动与线振动不相耦合，但是由于橡胶材料弹性模量与剪切模量差异大，减振系统不具备三向等刚度特性，系统共振点较多。目前，通过改变减振橡胶的几何形状或拓扑结构，使减振器具备三向等刚度特性的方法的确有效，但这增加了设计与制造上的复杂度。

2）通过改进减振器的布置方式，使8个减振器在平台台体顶端部位斜角布置，系统仍满足振动解耦的条件，并且若平台在三向分别发生单位位移时，减振橡胶的受拉压部分与受剪切部分的比例基本相同，系统具备三向等刚度特性。模态分析得出，改进布置方式后的平台减振系统3个线振动固有频率基本相等，3个角振动固有频率也基本相等，这减少了惯导平台系统的共振频率点，有利于最大程度抑制角偏移。随机振动分析结果显示了改进布置方式对于降低振动量级的有效性。

［1］ 周徐昌，沈建森.惯性导航技术的发展及其应用［J］.兵工自动化：自动测量与控制，2006，25（9）：55－59.

Zhou Xuchang，Shen Jiansen.Development of inertial navigation technology and its applications［J］.Ordnance Industry Automation：Automatic Measurement and Control，2006，25（9）：55－59.（in Chinese）

［2］ 李宇燕.金属橡胶隔振器的应用研究［J］.飞航导弹，2009，5（5）：62－63.

Li Yuyan.Application study of the metal rubber damper［J］.Winged Missiles Journal，2009，5（5）：62－63.（in Chinese）

［3］ 姚起杭，葛祖德，潘树祥，等.航空用金属丝网减振器的设计研制［J］.机械科学与技术，2002，21（S）：20－22.

Yao Qihang，Ge Zude，Pan Shuxiang，et al.Design and development of aviation wiry netting isolator［J］.Mechanical Science and Technology，2002，21（S）：20－22.（in Chinese）

［4］ 马芳贤，王会利，牟让科.航空用新型金属橡胶减振器设计分析研究［J］.振动工程学报.2008，21（S）：106－110.

Ma Fangxian，Wang Huili，Mu Rangke.A metal rubber shock absorber design analysis［J］.Journal of Vibration Engineering，2008，21（S）：106－110.（in Chinese）

［5］ 吕振华，范让林.动力总成—悬置系统振动解耦设计方法［J］.机械工程学报，2005，41（4）：49－54.

LüZhenhua，Fan Ranglin.Design method for vibration uncoupling of powerplant－mounting system［J］.Chinese Journal of Mechanical Engineering，2005，41（4）：49－54.（in Chinese）

［6］ Cyril M H，Allan G P.Harris′shock and vibration handbook［M］.5th ed.New York：McGraw Hill，2002：1－56.

［7］ Tuo Zhouhui，Hu Dewen，Li Ruhua，et al.Damping design of strapdown inertial navigation system［J］.Journal of Chinese Inertial Technology，2009，17（6）：648－650.

［8］ 姚建军.捷联惯导系统不同隔振模式的比较［J］.强度与环境，2009，36（2）：19－27.

Yao Jianjun.Contrast of different vibration isolation patterns used in strap－down inertial navigation system［J］.Structure and Environment Engineering，2009，36（2）：19－27.（in Chinese）

［9］ 张志鑫，张大伟.捷联惯组减振系统角振动、线振动共振频率理论分析［J］.中国惯性技术学报，2009，17（6）：654－657.

Zhang Zhixin，Zhang Dawei.Theory analysis on resonance frequencies of linear vibration and torsional vibration of strapdown IMU damping system［J］.Journal of Chinese Inertial Technology，2009，17（6）：654－657.（in Chinese）

［10］杨振兴，荣见华，傅建林.三维结构的频率拓扑优化设计［J］.振动与冲击，2006，25（3）：44－48.

Yang Zhenxing，Rong Jianhua，Fu Jianlin.Frequency topology optimal design of three－dimensional structures［J］.Journal of Vibration and Shock，2006，25（3）：44－48.（in Chinese）

［11］王明旭，陈国平.基于结构能量准则的阻尼器位置及参数优化［J］.振动、测试与诊断，2011，31（6）：754－758.

Wang Mingxu，Chen Guoping.Optimization on placement and parameters of damping design using energy criterion［J］.Journal of Vibration，Measurement and Diagnosis，2011，31（6）：754－758.（in Chinese）