建立斜拉桥基准有限元模型的新方法与实现＊

王海龙， 刘 杰， 王新敏， 张志国

（1.西南交通大学土木工程学院 成都，610031） （2.河北建筑工程学院土木工程学院 张家口，075024）（3.石家庄铁道大学土木工程学院 石家庄，050043）

引 言

损伤识别是进行桥梁承载力评估和制定维修养护策略的前提［1］，建立基准有限元模型是关键问题之一。以此为基准方可进行模态分析、指纹分析、损伤识别与诊断等后续分析工作。一般情况下，为获得基准有限元模型需要进行模型修正，修正后的有限元模型结果应趋于相应试验结果。获得的基准有限元模型既是桥梁结构的健康模型，也是未来损伤桥梁的参考模型［2-4］。目前，有限元模型修正的各种算法［5-9］中，无论是基于动力的算法（如最优矩阵法、设计参数型法和频响函数法等），还是基于静力的算法，以及动静结合算法等都需要进行迭代运算［10］。迭代运算过程中，当有限元模型计算值与实测值之间的差异高于所定义的阈值时，需要更新模型重新计算，反复迭代直至差值低于阈值。对于斜拉桥等大型结构，这些算法不但计算工作量巨大，而且有时难以达到预期目标。

笔者提出了一种建立斜拉桥基准有限元模型的新方法。首先，利用Ansys软件在初始位置进行建模，建模时不考虑主梁预拱度、变形和桥塔变形等状态，通过影响矩阵法计算出索力、位移和应变等参数的影响矩阵及相关向量；然后，利用Matlab软件的优化函数，以斜拉索的初应变为决策变量，通过设定目标函数和约束条件计算出斜拉索的初应变；最后，将此初应变赋给Ansys模型中的斜拉索单元，计算并获得与目标函数、约束条件相吻合的后处理结果。该方法可使Ansys计算结果与成桥试验的试验结果相吻合，获得的计算模型即为基准有限元模型。不过，该方法中经Matlab软件优化出的初应变是为获取基准有限元模型而选择的修正参数，不同于设计或施工斜拉桥时张拉索力对应的初应变。另外，因斜拉桥的非线性原因，优化出的初应变与实测索力不满足胡克定律。

1 基准有限元模型的修正方法与实现过程

1.1 修正方法

建立基准有限元模型不是利用影响矩阵进行成桥状态设计或施工阶段控制，笔者主要介绍与传统影响矩阵法不同的地方。关于成桥状态设计或施工阶段控制的影响矩阵法的基本原理和过程参见文献［11－14］。

斜拉桥示意如图1所示。斜拉索共有N＝n＋n′根，0＃、合龙段、支架现浇段无斜拉索。主梁划分为n＋n′＋5段，每段主梁的单元数假设为r，则主梁的节点数M＝r（n＋n′＋5）＋1。

图1 斜拉桥示意图Fig.1 Sketch map of cable－stayed bridge

假设在结构自重、二期荷载以及主梁和桥塔横梁预应力等各种荷载作用下，主梁位移满足叠加原理。设主梁各节点位移的斜拉索影响矩阵为E，斜拉索对应的初应变向量为x，斜拉桥在自重、二期恒载以及预应力荷载作用下产生的主梁位移向量为D，则影响矩阵法的主梁位移y可表示为

影响矩阵为

矩阵元素eij定义如下：当第j根斜拉索为单位初应变，其余所有斜拉索不施加初内力（即松弛状态下的初应变）时，主梁节点或截面i处的位移。

设斜拉索索力的影响矩阵为F，斜拉桥在自重、二期恒载和预应力荷载作用下斜拉索索力向量为T，则影响矩阵法的斜拉索索力方程可表示为

要使斜拉索的计算索力与实测索力尽量接近，可采用最小二乘法进行优化。取目标函数为

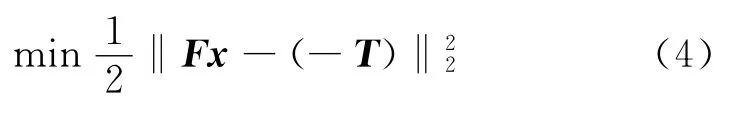
为保证主梁位移与实测位移相一致，需添加主梁位移的约束条件。另外，由于斜拉索不能承受压力，故需保证求得的斜拉索初应变为正数。约束条件为

其中：R为实测位移。

当测点数量不足时，可根据主梁位移的连续性，采用插值方法推算相应节点位移。

可利用该方法建立主梁内力、桥塔内力或位移的影响矩阵方程，在保证主梁内力、桥塔内力或位移吻合的前提下使斜拉索的计算索力与实测索力尽量接近。

按此方法，优化后可一次得到斜拉桥的基准有限元模型。该方法既能保证计算索力与实测索力相吻合，又能使主梁线形、内力或桥塔位移、内力与实测值基本一致。

1.2 实现过程

Ansys建模过程中，主梁预应力和桥塔横梁的预应力采用等效荷载法，先推导出直线与曲线力筋在各节点上的荷载分布情况，然后在节点上施加集中力和弯矩。主梁和桥塔采用beam188单元，该单元通过定义截面的方式输入且能实现变截面，通过导入AutoCAD截面图的方式定义截面，以减少利用Ansys直接绘制大量截面的工作量。斜拉索采用具有仅拉或仅压功能的link10单元。考虑斜拉桥的非线性，如斜拉索的垂度效应和梁－柱效应，打开大变形开关，垂度效应采用Ernst等效弹性模量法［5］设定斜拉索的弹性模量。

本研究方法的关键环节是计算位移和内力对应的各种影响矩阵和向量。因该环节的Ansys实现技术与传统方式不同，特以确定主梁位移向量y为例，说明其实现方法，并给出Ansys实现代码。

由式（1）可知，需先确定向量D和矩阵E。为能准确地计算出向量D，根据影响矩阵法的基本原理并结合link10单元特点，先将所有斜拉索的初应变置为－1，这样所有斜拉索将处于松弛状态，即使在自重、二期恒载以及预应力荷载等作用下主梁和桥塔发生变形时斜拉索中也不会有索力，可求出在非索力荷载作用下的向量D。计算矩阵E某列元素时，将该列元素对应的斜拉索初应变值取1%而不能取1，方能保证正确施加。其余斜拉索初应变置为－1，对每根斜拉索依次计算即可求得矩阵E所有元素。将向量D和矩阵E存放到文本文件中供Matlab调用。

向量D的Ansys实现过程为：

1）设置求解选项，包括静力计算、大变形、预应力效应和自动时间步等；

2）修改实常数并求解，将每根斜拉索的初应变置为－1；

3）创建文本文件用来存放向量；4）获取主梁节点数；

5）获取主梁各节点的位移；

6）将向量按一定格式写入文本文件。

其详细代码如下：

据此代码一步即可获得向量D所有元素，并按格式存入TXT文件中。确定矩阵E的过程与确定向量D类似，确定向量T与确定向量D方法也类似，不再赘述。

确定矩阵F与确定向量D的过程有所不同，开始时所有斜拉索的初应变应置为0而不能置为－1。这主要是因为将斜拉索都设成松弛状态的情况下，计算不出某根斜拉索对其余所有斜拉索的影响。

优化的实现采用Matlab软件，调取文本文件中数据赋值给向量和矩阵，利用最小二乘函数进行优化，包括给变量赋值、利用最小二乘函数优化、优化结果保存为Excel文件等步骤，实现代码如下。

大型结构的优化在1min内即可优化成功。根据优化的斜拉索初应变重新计算，即可获得与Matlab优化结果非常接近的主梁线形及斜拉桥内力。

2 算 例

以某座斜拉桥为例，主桥为上跨铁路的单塔双索面预应力混凝土斜拉桥，采用塔梁固结的形式。斜拉索采用扇形布置，梁上的索距为6m。桥跨为130m＋130m，两跨对称布置18对斜拉索。主梁采用预应力混凝土倒梯型的单箱四室截面，主梁中间设三道直腹板，两侧设斜腹板，端部为风嘴形状。主梁顶面全宽为37.5m，直线上标准段顶面设双向2%横坡。标准断面梁高为3m，塔梁固结区加高到3.5m。主梁标准断面底板宽为21.9m，底板厚为28cm，顶板厚为28cm，斜边腹板厚为28cm，中间直腹板厚为40cm。箱梁外侧悬臂宽为1.55m，厚为100cm。顺桥向根据拉索间距设置横梁，横梁腹板厚为40cm。斜拉桥结构模型如图2所示。

图2 斜拉桥结构模型Fig.2 The Structure Model of cable－stayed bridge

利用本研究方法计算出影响矩阵和向量后，用Matlab软件计算斜拉索初应变，如表1所示。将结果存入Excel文件中，供Ansys调用。

表1 斜拉索初应变优化结果Tab.1 Optimal results of initial strain of cable－stayed bridge

由表1可看出，两个方向斜拉索初应变基本相同，与桥梁对称的实际情况相符。由于经过优化计算，个别斜拉索的初应变左右略有较小差别，可忽略不计。Ansys调用Matlab生成的Excel文件获取斜拉索初应变，进行求解获得计算结果。基准有限元模型位移情况如图3所示。

图3 斜拉桥位移图（单位：mm）Fig.3 Displacement plot of cable－stayed bridge（unit：mm）

计算结果与成桥实测结果对比如图4和图5所示。

图4 斜拉桥主梁位移对比图Fig.4 Displacement contrast curve of calculated and measured values

图5 斜拉桥斜拉索索力对比图Fig.5 Cable force contrast curve of calculated and measured values

由图4、图5可知，主梁线形及索力与实测值吻合非常好，实现了模型修正的目的。

3 结 论

1）通过修正斜拉索初应变实现模型修正的方法可行、有效，能方便、快速地获得与成桥试验数据相吻合的斜拉桥基准有限元模型。

2）该方法不需要任何迭代，经过优化，一步就能找到斜拉索的初始应变，具有计算代价低的特点。

3）因该方法简便快速，可考虑应用到斜拉桥实时健康监测和在线模型修正中。

［1］ 杨小森，闫维明，陈彦江，等.基于模型修正的大跨斜拉桥损伤识别方法［J］.振动、测试与诊断，2012，32（2）：276－281.

Yang Xiaosen，Yan，Weiming，Chen Yanjiang，et al.Damage detection method for long span cable－stayed bridge based on model updating［J］.Journal of Vibration，Measurement ＆ Diagnosis，2012，32（2）：276－281.（in Chinese）

［2］ 李惠，欧进萍.斜拉桥结构健康监测系统的设计与实现（Ⅰ）：系统设计［J］.土木工程学报，2006，39（4）：39－44.

Li Hui，Ou Jinping.Design and implementation of health monitoring systems for cable－stayed bridges（I）：design methods［J］.China Civil Engineering Journal，2006，39（4）：39－44.（in Chinese）

［3］ 李惠，欧进萍.斜拉桥结构健康监测系统的设计与实现（Ⅱ）：系统设计［J］.土木工程学报，2006，39（4）：45－53.Li Hui，Ou Jinping.Design and implementation of health monitoring systems for cable－stayed bridges（Ⅱ）：design methods［J］.China Civil Engineering Journal，2006，39（4）：45－53.（in Chinese）

［4］ Zong Zhouhong，Wang T L，Huang D Z，et al.Stateof－the－art report of bridge health monitoring［J］.Journal of Fuzhou University：Natural Science，2002，30（2）：122－157.

［5］ 辛克贵，刘钺强，杨国平.大跨度斜拉桥恒载非线性静力分析［J］.清华大学学报，2002，42（6）：818－821.

Xin Kegui，Liu Yueqiang，Yang Guoping.Nonlinear static analysis of lang－span cable－stayed bridges under dead loads［J］.Journal of Tsinghua University，2002，42（6）：818－821.（in Chinese）

［6］ 叶梅新，韩衍群，张敏.基于Ansys平台的斜拉桥调索方法研究［J］.铁道学报，2006，28（4）：128－131.

Ye Meixin，Han Yanqun，Zhang Min.Research on adjusting cable forces of cable－stayed bridges based on Ansys［J］.Journal of The China Railway Society，2006，28（4）：128－131.（in Chinese）

［7］ 任伟新，彭雪林.青洲斜拉桥的基准动力有限元模型［J］.计算力学学报，2007，24（5）：609－614.

Ren Weixin，Peng Xuelin.Baseline dynamic finite element model of Qingzhou cable－stayed bridg ［J］.Chinese Journal of Computational Mechanics，2007，24（5）：609－614.（in Chinese）

［8］ 李建慧，李爱群，缪长青，等.润扬大桥修正斜拉索力的基准有限元模型［J］.东南大学学报：自然科学版，2007，37（2）：266－269.

Li Jianhui，Li Aiqun，Miao Changqing，et al.Baseline FE model to revise cable forces in Runyang Cable－Stayed Bridge［J］.Journal of Southeast University：Natural Science Edition，2007，37（2）：266－269.（in Chinese）

［9］ 姚昌荣，李亚东.基于静动力测试数据的斜拉桥模型修正［J］.铁道学报，2008，30（3）：65－70.

Yao Changrong，Li Yadong.Updating of cable－stayed bridges model based on static and dynamic test data［J］.Journal of the China Railway Society，2008，30（3）：65－70.（in Chinese）

［10］ 宗周红，任伟新.桥梁有限元模型修正和模型确认［M］.北京：人民交通出版社，2012：1－8.

［11］施笃铮，汪劲丰，项贻强，等.斜拉桥施工过程中的索力控制与优化研究［J］.中国公路学报，2002，15（2）：57－60.

Shi Duzheng，Wang Jinfeng，Xiang Yiqiang，et al.Optimum tensioning in construction state of cable－stayed bridge［J］.Chian Journal of Highway and Transport，2002，15（2）：57－60.（in Chinese）

［12］梁鹏，肖汝诚，张雪松.斜拉桥索力优化实用方法［J］.同济大学学报：自然科学版，2003，31（11）：1270－1274.

Liang Peng，Xiao Rucheng，Zhang Xuesong.Practical method of optimization of cable tensions for cablestayed bridges［J］.Journal of Tongji University：Natural Science，2003，31（11）：1270－1274.（in Chinese）

［13］张建民，肖汝诚.千米级斜拉桥施工过程中主梁的线形控制［J］.同济大学学报：自然科学版，2004，32（12）：1567－1572.

Zhang Jianmin，Xiao Rucheng.Study on linear control of girders in construction state for a thousand－meter scale cabIe－stayed bridge［J］.Journal of Tongji University：Natural Science，2004，32（12）：1567－1572.（in Chinese）

［14］闫维明，张志，陈彦江，等.大跨度斜拉桥施工过程中的索力控制方法［J］.土木建筑与环境工程，2010，32（5）：130－134.

Yan Weiming，Zhang Zhi，Chen Yanjiang，et al.Method of cable tension controlling in the long－span cable－stayed bridge construction［J］.Journal of Civil Architectural Environmental Engineering，2010，32（5）：130－134.（in Chinese）