基于IIR结构的自适应滤波振动主动控制方法＊

黄全振， 吕宽洲， 李恒宇， 王小华

（1.河南工程学院电气信息工程学院 郑州，451191） （2.上海大学机电工程与自动化学院 上海，200072）

引 言

随着航天事业的飞速发展，越来越多的柔性外伸结构被用到航天器上，如太阳能帆板、大型空间可展开反射器以及大型精密天线、柔性机械臂等。当这些结构在太空环境中发生非正常振动时，由于太空环境几乎没有外阻，且其部件自身又具有柔性大、内阻低等特点，导致结构振动的衰减速度非常缓慢。这些部件若长期处于振动状态，将引起结构的疲劳损伤，最终影响整个航天器的使用寿命；因此，航天器柔性外伸结构的振动控制问题历来是航天器设计中的一个重要课题和难点［1-2］。

在航天器柔性部件中，太阳能帆板是一种比较具有代表性的大型柔性结构。近年来，许多学者模拟太阳能帆板为研究对象，对其开展振动主动控制的研究［3-5］。在太阳能帆板的振动主动控制研究过程中，控制策略一直是其研究的核心内容之一。由于自适应滤波控制方法具有控制修正速率高、对非平稳响应适应能力强，并能够较快跟踪结构参数及外扰响应变化的特性，近年来在振动主动控制研究领域获得广泛关注。目前，应用在振动控制领域里的自适应滤波控制方法大多是基于最小均方的LMS（least mean square）［6-8］控制算法，如基于有限冲击响应FIR滤波器结构的滤波－X最小均方（FXLMS）算法［9-10］和基于无限冲击响应IIR 滤波器结构的滤波－U 最小均方（FULMS）算法［11-13］等。上述文献的研究内容，大多数属于理论公式的推导和数值模拟计算仿真，而通过实际试验验证的较少。

笔者采用机敏压电柔性板来模拟太阳能帆板作为振动控制系统控制对象，鉴于FXLMS控制算法需要预知与外激扰信号相关的参考信号这一缺陷，同时考虑到实际的振动控制过程中单输入单输出模式控制效果的有限性，提出一种基于IIR滤波器结构的多输入多输出模式的自适应振动控制方法。首先，给出了基于IIR模式控制器设计思路，详细分析了控制算法的推理过程；其次，建立模拟太阳能帆板的试验模型，在此基础上搭建振动主动控制系统试验平台；然后，分别进行了FXLMS算法、单输入单输出FULMS算法和多输入多输出FULMS算法仿真对比分析；最后，针对多输入多输出FULMS算法进行试验验证。结果表明其振动控制效果良好，从而印证了所提的控制器结构与自适应算法的有效性和可行性，且具有快速收敛以及较低阶模型都能满足控制性能要求的优势。

1 基于IIR结构的自适应控制器设计

实现结构振动主动控制的自适应滤波控制方法，是以抵消外扰引起的受控对象的响应为出发点，其基本思想是设计出这样的自适应滤波形式控制器，它的输出通过作动器产生控制力作用于受控对象，使受控对象中对振动水平有一定要求的位置上的响应与外扰在这些位置上的响应相抵消，达到消除或减小受控对象振动响应的目的。具体到控制器设计，基于IIR模式控制器的振动反馈环节可以适应参考信号的直接结构选取策略。从控制器设计和自适应算法分析简单性考虑，多通道基于FULMS算法控制器结构设计如图1所示。

图1 FULMS算法振动控制结构图Fig.1 Schematic of filtered－U LMS vibration control algorithm

如图1所示，该控制系统具有M个控制器和L个传感器，外扰输入信号经过传输通道H1之后产生受控对象L维的外激扰响应输出向量B（k），E（k）为受控对象L维响应误差输出向量（对应L个传感器）。无控时，B（k）＝E（k）。x（k）为滤波器在k时刻的输入，为参考信号，应当与原始外扰输入信号有较高的相关性。Y（k）为M维控制器k时刻的输出向量（对应M个控制器），Z（k）为施加控制时L维控制响应输出向量。H1，H2分别为描述外扰通道和控制通道特性的结构模型参数向量。H＊2为H2的识别模型参数矩阵，是M×L维，其中每个元素都是P维向量，表示每个滤波器通道都选择P阶FIR滤波器描述结构模型。W为一个对应FIR滤波器输入信号序列的控制器加权系数矩阵，是一个M×N阶的矩阵，N为该滤波器参考信号的阶数。Wi为第i个控制器加权系数向量，wij为第i个控制器加权系数向量的第j阶元素。D为一个对应Q阶FIR滤波器控制信号序列系数的加权系数矩阵，是M×Q维矩阵，diq（k）为第k时刻的反馈滤波器第i个控制器输出信号加权系数向量的第q阶元素。R（k）为滤波－X信号矩阵，由X（k）经H＊2环节得到。G（k）也是滤波－X信号矩阵，由Y（k）经H＊2环节得到。

2 FULMS算法推理分析

在构建IIR模式控制器结构与确定受控结构系统模型参数的基础上，可采用数字信号处理技术求得最优控制器参数，实现的核心是自适应控制算法，它根据测得的新信息实时调整控制器参数，保证控制效果始终趋于最优，所依据的寻优准则一般为最小均方准则。

IIR滤波器结构的输入输出关系定义为

其转移函数可表示为

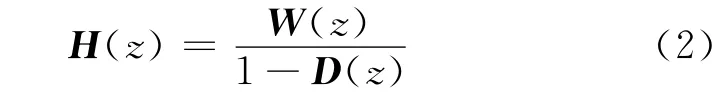
式（2）中W（z）和D（z）分别表示为

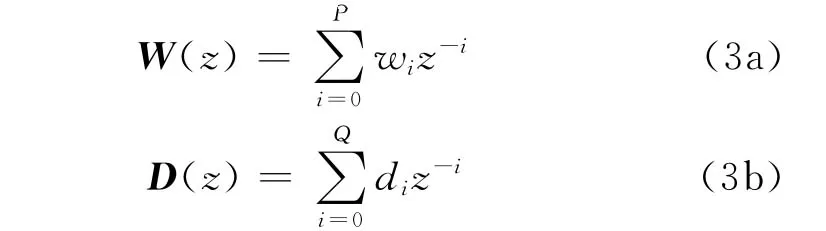
从其转移函数的表达式就可以明显地看出其包含零点和极点，而且在实际振动控制过程中，参考信号传感器所提取的参考信号都会含有控制输出信号的成分。控制输出信号对参考信号的影响反映在传输函数上就是极点的引入，控制输出的反馈信号导致了模型中包含了极点，从而更好地反映控制输出信号对参考信号的影响。

由于多输入多输出FULMS控制算法无论从收敛速度还是从收敛效果上都要优于单输入单输出控制算法，因此重点关注多通道的FULMS算法。其结构原理如图1所示，其算法模型由一个FIR滤波器和一个反馈的FIR滤波器组成。其控制输出Y（k）由权值矩阵W＊（k）和输入向量U（k）得出，其中

其中：p和q为延迟量。

类似于FXLMS算法的得名，依据输入向量U（k），因此该算法被称为FULMS算法。其多输入多输出算法过程如下

其中：

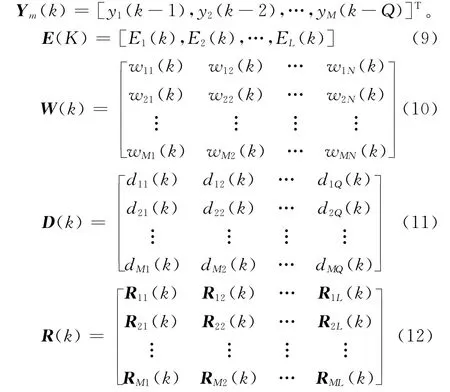
其中：

其中：Gml（k）＝

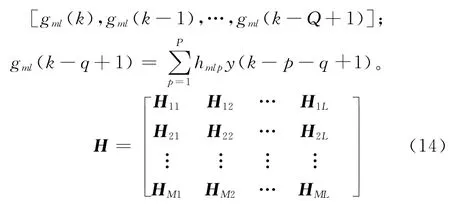
其中：Hml＝ ［hml1，hml2，…，hmlP］。

综上所述，多输入多输出FULMS算法可表示为

其中：

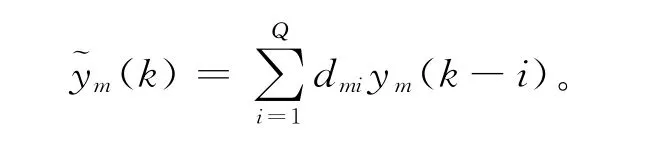
3 试验平台的搭建

3.1 试验模型设计

选用环氧树脂柔性板进行模拟航天太阳能帆板。为了试验方便，将模型柔性板一端固定，形成悬臂梁结构，其大小尺寸为：长度L＝1 200mm；宽度B＝300mm；厚度h＝2mm。同时为一定程度上减少环氧树脂板的柔性约束，增大其自由摆动的柔软性能，决定对固定端的根部进行裁剪，切成三角形的底、高尺寸分别约为50mm×110mm。柔性板的主要参数如下：弹性模量为65GPa；泊松比为0.3；密度为7 500kg／m3。其试验帆板结构示意图如图2所示。

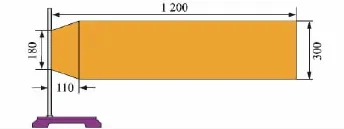
图2 试验帆板结构示意图（单位：mm）Fig.2 Schematic diagram of the test board structure（unit：mm）

依据模态应变能的准则进行传感器、作动器的位置布放，其准则的大致思想是具有较大模态应变能的位置，其振动响应也比较大，将传感器和驱动器合理配置在模态应变最大处，尽量提高振动主动控制的效率。考虑到试验模型结构的振动能量主要集中在较低阶振动模态，采用ANSYS有限元分析软件，对试验模型结构进行模态分析，得出试验模型前6阶弯曲应力分布图，从而为传感器和作动器的分布配位提供设计思路支持。试验模型悬臂梁前6阶固有频率如表1所示，试验模型结构低阶模态应力分布图如图3所示。

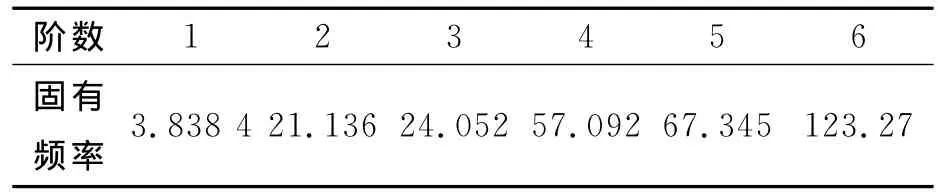
表1 悬臂梁前6阶固有频率表Tab.1 The first six order natural frequency of cantilever beam Hz

图3 试验模型结构模态分析图Fig.3 Modal analysis of the test model structure

由图3可知，结构振动应力分布主要集中在靠近固定端根部附近，该处结构形变也相应最大，在此位置布置压电传感器与作动器的测控效果最为明显；同时考虑到各阶振动模态的应力分布具有相对集中区域，则综合考虑在相关位置进行压电传感器／作动器的配位布置。在此基础上，通过激振器对柔板试验模型进行模态激励，也验证了ANSYS的分析结果，基本符合试验模型结构的实际振动情况。图4所示为压电传感／驱动网络配位布置示意图。

图4中，将传感器与作动器布置为4组测量通道和4组控制通道的多输入多输出系统，具体分组为：每片压电传感器就是1个测量通道，图中4个传感器分别编号1～4，即传感器有4个通道；每一竖排的压电片作为1组驱动单元，次根部两组组合成一个通道，另外3组分别是3个通道，编号分别是1～4；最根部一组为激励通道，即给试验模型结构施加外干扰的信号组，同时为增强驱动能力，在帆板模型结构双面进行作动器的粘贴。本试验选用的传感PZT的尺寸为40mm×8mm×1mm，质量为1.67g；压电PZT作动器尺寸为65mm×30mm×2mm，质量为30g；激励通道组与作动器选用一样的型号。

图4 压电传感／驱动网络配位布置示意图（单位：mm）Fig.4 Schematic diagram for locations of piezoelectric sensors and actuators（unit：mm）

3.2 振动控制系统试验平台

压电机敏柔性结构振动主动控制系统试验平台主要由试验平台构架、试验模型对象、高性能计算机、高速数据AD采集卡与DA输出卡、信号发生器、低通滤波器、示波器、功率放大器，以及相关测控单元等组成。试验平台构架包括支撑钢板结构，其长、宽、高的具体尺寸为600mm×600mm×25mm，并在铺垫橡胶垫的基础上安装于支撑试验台面上，以尽量减小模型对象振动响应向基础试验台面的传递。试验台架安装有悬臂固支杆、导线接线排等。高速数据AD采集卡为研华公司的PIC－1712，DA输出卡为研华公司的PIC－1721，两卡均为12位精度、PCI连接方式，并与高性能计算机构成核心控制器硬件部分，整体试验平台构成如图5所示。

图5 结构振动试验平台照片Fig.5 Photo of the experimental platform

在构建试验平台的基础上，基于VC6.0平台开发了相关测控软件，以保障系统功能的实现与控制过程的实施。基本控制过程为：首先，利用信号发生器输出一个持续信号，经过功率放大器作用到作为激振器的压电片上，使试验模型结构处于持续激励状态；其次，压电传感网络获取的多路结构振动信号，经信号调理后由AD卡实现多路采集，并由计算机构成的控制器运算控制算法，同时产生多路输出控制量由DA卡输出；最后，经功率放大器驱动压电作动网络，以实现模型结构振动响应的多通道自适应控制。

4 试验分析与验证

4.1 仿真试验分析

根据太阳能帆板的实际运行情况，对其影响比较大的振动主要集中在低频部分。取其能量最集中的第2阶纯弯曲频率的谐波信号输入，即21.136Hz的正弦信号，进行主动振动仿真试验，则该外扰信号可以表示为x（n）＝sin（2πn×21.136）。从试验模型板可知，参考信号取之于参考信号传感器，它测到的信号应为外扰信号与反馈控制信号的叠加。考虑到参考信号采集传感器粘贴于激振源附近，并且远离控制作动器，导致参考传感器测得的信号主要为激振外扰信号，而反馈控制信号比较小，更加接近于实际。在仿真过程中，参考信号的取值为Aref（n）＝sin（2πn×21.136）－0.1Bout（n），Bout（n）为控制输出信号。

为验证笔者所提出的多通道FULMS算法的优越性和有效性，在相同试验参数与环境下，分别进行多通道FXLMS算法［10］、单通道FULMS算法和多通道FULMS算法仿真对比试验。具体仿真试验参数的选取为：控制通道参数模型选用离线辨识方法，选取其中一路辨识结果H［1］［1］＝［0.837 473 0.238 032 0.905 207－0.429 774 0.940 230－0.164 034－0.488 190－0.195 506 0.883 447 0.809 109－0.762 016 0.321 118 0.155 496 0.975 906 0.949 385 0.451 797－0.815 248－0.281 369 0.047 096 0.293 741 0.751 860－0.138 281 1.084 713－0.840 447］，若 FXLMS仿真试验，滤波器长度为24，收敛步长μ＝0.06；若前馈滤波器长度为16，反馈滤波器长度也为12，前馈收敛步长为μ＝0.08，反馈前馈收敛步长为a＝0.04。

多通道FXLMS算法振动控制仿真试验结果如图6所示。

图6 多通道FXLMS算法振动控制仿真结果Fig.6 Simulation result of MIMO FXLMS vibration control algorithm

单通道FULMS算法振动控制仿真试验结果如图7所示。

多通道FULMS算法振动控制仿真试验结果如图8所示。

图7 单通道FXLMS算法振动控制仿真结果Fig.7 Simulation result of SISO FULMS vibration control algorithm

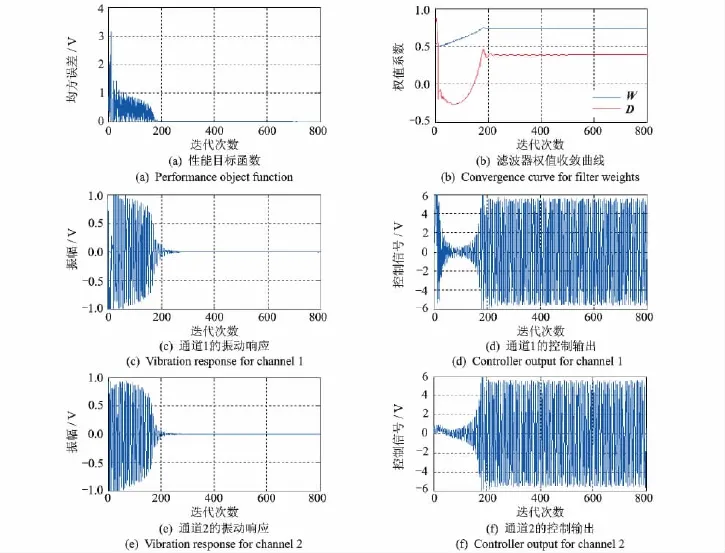
图8 多通道FULMS算法振动控制仿真结果Fig.8 Simulation result of MIMO FULMS vibration control algorithm

由图6，7，8试验结果对比可以看出，在相同条件下，多通道FXLMS算法在300步以后，两个通道的振动响应得到了大幅度的抑制，并基本趋于稳定状态，但振动响应不能被完全抑制；单通道FULMS算法大约在300步以后，其振动响应被完全抑制；多通道FULMS大约在200步以后，两个通道的振动响应被完全抑制，从而验证了笔者所提出的多通道算法的优越性。

从上述仿真试验可知，当控制反馈信号对参考信号影响较大时，采用FXLMS算法几乎无法达到完全抑制振动响应的目的，而FULMS算法由于其传递函数结构中有一个反馈控制环节，可以弥补这一问题。由于反馈步长因子α的选取比较重要，若选取不当，将引起控制系统的发散，所以需根据具体实际情况选取，其大致原则为小于前馈步长因子μ。参考信号的合适提取，对主动抑振的顺利成功影响较大，采用激振信号叠加控制反馈的方法，可以较好地满足仿真的真实性要求。

4.2 试验验证与分析

为了直观显示控制算法效果，选取FREQ2为21.136Hz的结构模态频率进行控制试验。首先，施加频率为f＝21.136Hz的激励信号并经功率放大器，持续激励试验模型根部的激励压电片上，使其处于振动状态；其次，PZT传感网络获取结构振动信号，依次经过电荷放大器、低通滤波器和高速数据AD采集卡送入工控机。图9所示为无控状态下的结构持续振动状况。工控机依据控制算法进行运算，输出控制信号，通过DA输出卡输出控制信号，经过功率放大后作用到作动器上，实现振动控制的目的，其控制试验结果如图10所示。

图9 无施加控制信号时结构持续振动状况Fig.9 Without control for structure vibration state

图10（a，b，c，d）分别为对应通道1、通道2、通道3和通道4的控制信号时间历程，自1s时刻开始施加控制信号，随后振动幅度很快获得有效抑制，振幅下降了约80%左右；图10（e）为结构振动响应总体控制效果图（即所有压电传感器所测振动响应信号之均方根值），施加控制后结构总体响应明显下降，表明结构总体振动获得有效抑制。

图10 多通道FULMS算法振动控制试验结果Fig.10 Control performance of MIMO filtered－U least mean square algorithm

5 结束语

笔者以机敏压电太空帆板结构为模拟试验对象，针对振动控制过程中控制反馈信号对参考信号的影响，着重分析基于IIR结构控制器的FULMS自适应滤波振动控制方法。由于在实际的振动控制中，单输入单输出的控制模式效果有限，因此提出了一种控制效果更为明显的多输入多输出模式的FULMS控制算法，主要包括控制器结构设计、控制算法推理过程和相关特性分析，并通过仿真和试验对其控制效果进行验证。分析结果表明，笔者所提算法具有更高的收敛速度及较好的控制效果，为自适应振动控制方法向实际工程应用提供了较好的研究基础。

［1］ Malekzadeh M，Naghash A，Talebi H A.Robust attitude and vibration control of nonlinear flexible spacecraft［J］.Asian Journal of Control，2012，14（2）：553－563.

［2］ 段丽玮，汤忠梁，吴志华.飞行器垂直尾翼H∞鲁棒振动主动控制［J］.振动、测试与诊断，2011，31（1）：119－123.

Duan Liwei，Tang Zhongliang，Wu Zhihua.Active vibration suppression of vertical tail using H∞robust control theory［J］.Journal of Vibration，Measurement＆ Diagnosis，2011，31（1）：119－123.（in Chinese）

［3］ Jiang Jianping，Li Dongxu.Optimal placement and decentralized robust vibration control for spacecraft smart solar panel structures［J］.Smart Materials ＆Structures，2010，19（8）：085020.

［4］ Foda M A，Alsaif K A.Vibration mitigation of composite laminated satellite solar panels using distributed piezoelectric patches［J］.Smart Materials and System，2012，10（2）：111－130.

［5］ 邱志成，张祥通.基于视觉的柔性结构振动测量及其控制［J］.振动、测试与诊断，2012，32（1）：11－16.

Qiu Zhicheng，Zhang Xiangtong.Vision－based vibration measurement and control of flexible structure［J］.Journal of Vibration， Measurement ＆ Diagnosis，2012，32（1）：11－16.（in Chinese）

［6］ Oh J E，Park S H，Hong J S，et al.Active vibration control of flexible cantilever beam using piezo actuator and filtered－X LMS algorithm［J］.Ksme International Journal，1998，12（4）：665－671.

［7］ Fraanje R，Verhaegen M，Doelman N.Convergence analysis of the filtered－U LMS algorithm for active noise control in case perfect cancellation is not possible［J］.Signal Processing，2003，83（6）：1239－1254.

［8］ Carnahan J J，Richards C M.A modification to filtered－X LMS control for airfoil vibration and flutter suppression［J］.Journal of Vibration and Control，2008，14（6）：831－848.

［9］ Yang Z D，Huang Q T，Han J W，et al.Adaptive inverse control of random vibration based on the filtered－X LMS algorithm［J］.Earthquake Engineering and Engineering Vibration，2010，9（1）：141－146.

［10］朱晓锦，高志远，黄全振，等.FXLMS算法用于压电柔性结构多通道振动控制［J］.振动、测试与诊断，2011，31（2）：150－155.

Zhu Xiaojin，Gao Zhiyuan，Huang Quanzhen，et al.Active vibration control for piezoelectric flexible structure using multi－channel FXLMS algorithm ［J］.Journal of Vibration，Measurement ＆Diagnosis，2011，31（2）：150－155.（in Chinese）

［11］Kim H W，Park H S，Lee S K，et al.Modified filtered－U LMS algorithm for active noise control and its application to a short acoustic duct［J］.Mechanical Systems and Signal Processing，2011，25（1）：475－484.

［12］Park J，Lee S.A novel adaptive algorithm with an IIR filter and a variable step size for active noise control in a short duct［J］.International Journal of Automotive Technology，2012，13（2）：223－229.

［13］Zhu Xiaojin，Gao Zhiyuan，Huang Quanzhen，et al.Analysis and implementation of MIMO FULMS algorithm for active vibration control［J］.Transactions of the Institute of Measurement and Control，2012，34（7）：815－828.