一种新型橡胶衬套理论模型及其参数识别*
左曙光, 李 凯, 吴旭东, 郭学良, 李程祎
(同济大学新能源汽车工程中心 上海,201804)
引 言
橡胶材料作为一种常用的工程减振材料,广泛应用于汽车各种减振系统中,如悬架衬套、发动机和变速箱悬置、排气系统吊耳等[1]。橡胶元件作为隔振元件,其动态性能对系统的振动控制和隔振设计起主要作用。目前,国内外对橡胶元件的研究中,静态特性的研究较多而且已经比较成熟,但对其动态特性的研究还不全面,原因是橡胶减振元件动态特性复杂,随频率、振幅而变化,具有非常强的非线性。针对橡胶材料动态特性,国内外学者提出了多种材料本构模型。复常数模量模型[2]简单根据应力-应变滞回曲线确定材料的复常数模量,其基本特征是非频变,与实际材料黏弹模量的频变特性并不相符。Kelvin-Voigt模型[3]由一线性弹簧和一阻尼器并联,能够明显地表现出材料的频率相关性,但在高频时高估了阻尼的贡献。三参数Maxwell模型将Kelvin模型中的阻尼器用一个由弹簧和阻尼器串联组成的Maxwell单元代替,能更准确地描述橡胶材料的动刚度特性,但对阻尼系数的描述不够准确。Wiechert模型将三参数Maxwell模型进行扩展,用多个Maxwell单元与之并联,从而能够在较宽的频率范围内对橡胶材料的动态特性进行较好的描述,但需要使用较多的参数才能保证模型的准确性,使得模型复杂且模型参数没有明确的物理意义[4]。描述振幅相关性的双线性模型、Bouc-Wen模型及Berg摩擦模型等[5-7]也存在精度不高、参数识别效率低等问题。
首先,笔者进行了橡胶衬套轴向的静、动态特性试验,根据试验结果对衬套动态特性的频率相关性和振幅相关性进行分析,提出一种基于弹性单元、摩擦单元和若干黏弹单元叠加的新型橡胶衬套模型;然后,根据具体的试验结果,提出黏弹单元个数的确定方法和一种新的参数识别方法;最后,通过与试验结果对比,模型能更为准确的描述衬套轴向的动态特性。
1 橡胶衬套静动态特性试验与分析
研究的对象是简单圆柱形橡胶衬套,橡胶衬套实物如图1所示。衬套由内外钢圈和中间的橡胶材料组成,图2为衬套的剖视图。首先,通过试验对衬套轴向的静动态特性进行了研究[8],试验夹具如图2所示。使用中通过固定外圈、激励内圈的方式,获得衬套轴向静动态特性。
1.1 橡胶衬套轴向静态特性试验
静态加载下,加载位移见表1,试验结果见图3。根据试验结果可以发现,衬套轴向力和位移的关系基本符合线性关系,说明衬套轴向在静态加载下具有线性的弹性特性。

图1 橡胶衬套实物图Fig.1 The picture of rubber bushing

图2 衬套轴向加载试验夹具Fig.2 The clamp for rubber axial-load test
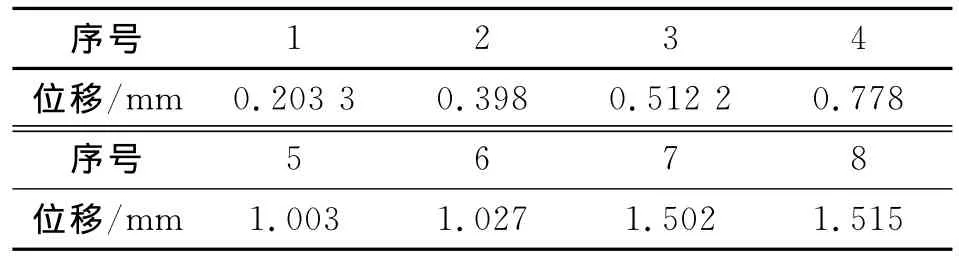
表1 衬套轴向静态加载位移Tab.1 The static axial-load displacement of rubber

图3 衬套轴向静态加载力与位移的关系Fig.3 The axial static loaded force versus displacement curve for bushing
1.2 橡胶衬套轴向动态特性试验
试验装置、夹具与静态加载时一致。通过高频液压油缸对橡胶衬套轴向施加不同频率和振幅的正弦位移激励,得到激励位移和响应力信号,进而获得两者的振动幅值。在5个频率下分别进行了6种振幅的试验,共计30个工况,具体频率和幅值见表2。衬套轴向的动态特性主要指衬套轴向动刚度及响应力与激励位移的滞后角。响应力幅值除以对应工况下激励位移的幅值表示衬套轴向的动态刚度特性。用激励位移和响应力信号的互功率谱得到两者的相位角差值,即滞后角。滞后角的正弦就是阻尼系数。试验结果如图4所示。
由上述试验结果得到以下结论。
1)频率一定,动刚度随振幅变化规律如图4(a)所示,阻尼系数随振幅变化规律如图4(c)所示。衬套轴向动刚度(阻尼系数)随振幅的增加而迅速降低,振幅对衬套动刚度(阻尼系数)的影响非常大。

表2 低频试验时激励振幅和频率的值Tab.2 The amplitude and frequency of excitation in low-frequency test
2)振幅一定,动刚度随频率的变化关系如图4(b)所示,阻尼系数随频率变化规律如图4(d)所示。动刚度(阻尼系数)几乎不随频率的变化而变化,同一振幅下,激励频率几乎不对衬套轴向动刚度(阻尼系数)产生影响。相比之下,阻尼系数受频率的影响要比动刚度大。
综上所述,在激励频率较低的情况下(20Hz以内),激励振幅是动态特性的决定性因素,激励频率几乎不对动态特性产生影响。
2 新型橡胶衬套轴向动态模型
上述试验结果反映出的动态特性与大部分研究中采用的动态模型表现出不同的特性,如将弹性单元和液体黏壶并联的K-V模型(图5)、将Maxwell单元与弹簧并联的Maxwell模型(图6)。这些模型的特点是动态特性随频率有明显的变化,但不随振幅而变化。
因此,笔者提出一种将体现弹性特性的弹性单元、体现振幅相关性的摩擦单元和体现频率相关性的若干黏弹单元并联的新型模型,来描述衬套轴向在激励频率较低时的动态特性。
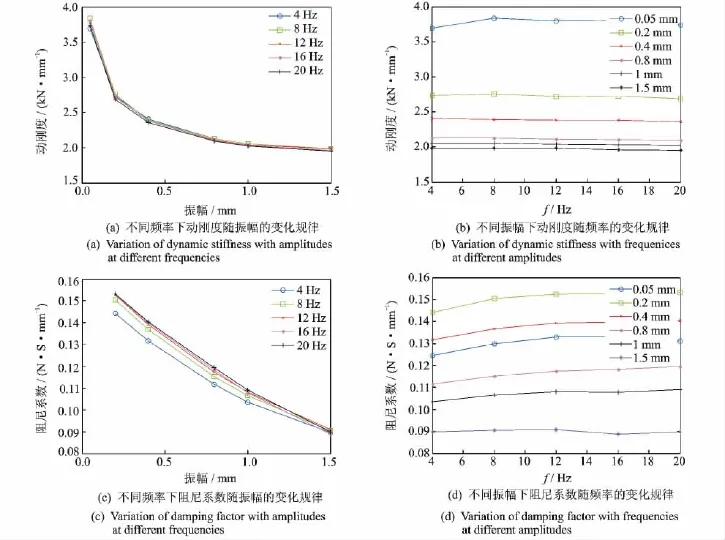
图4 低频试验动态特性Fig.4 The dynamic characteristics in low-frequency test

图5 K-V模型示意图Fig.5 K-V model

图6 Maxwell模型示意图Fig.6 Maxwell model
2.1 模型组成
2.1.1 弹性单元
根据试验结果发现,衬套轴向弹性特性符合胡克定律,因此用胡克定律的形式表示衬套轴向的弹性特性

弹性单元在一个正弦激励周期中,不损耗能量,即Ee(x)=0。当激励振幅为x0时,响应力的振幅为F0=Kex0。
2.1.2 摩擦单元
摩擦单元是指一种类似摩擦力特性的激励位移和响应力的关系,主要用于描述动态特性的振幅相关性。由于Berg模型参数识别简单,且能比较准确地描述橡胶元件的振幅相关性,得到了比较广泛的应用[9-11]。因此,笔者采用Berg摩擦模型描述橡胶材料的振幅相关性。Berg模型的摩擦力Ff取决于摩擦单元两端的相对位移,同时也与摩擦力位移曲线上的参考点(xs,Ffs)有关,其具体表达形式如下。
当x=xs时

当x>xs,或x增加时

当x<xs,或x减小时

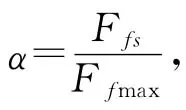
本模型中,摩擦单元在一个周期中,力的幅值Ff0为

其中:x0为激励位移的幅值。
一个周期中损耗的能量Ef为

其中:α0=Ff0/Ffmax。
2.1.3 黏弹单元
Maxwell单元是指将一个线性弹簧与一个液体黏壶串联来表示橡胶材料力学特性的模型。笔者建立的黏弹模型是利用多个Maxwell模型并联的形式,如图7所示来表示橡胶材料的黏弹特性。Maxwell单元的个数需要根据部分试验数据进行确定。

图7 黏弹单元示意图Fig.7 The visco-elastic elements
第i个黏弹单元的动态刚度复数形式为

其中:w为激励圆频率;Ei和ηi分别为第i个Maxwell单元弹簧的刚度值和黏壶的阻尼值。
第i个Maxwell单元整体表现出的阻尼为

其中:在简谐激励的条件下,Wi和A0分别为每个循环工况所损耗的能量和激励的幅值为复刚度的模;δi为阻尼角。
对i个分量进行矢量叠加,可得到总的黏弹单元的动刚度和阻尼值
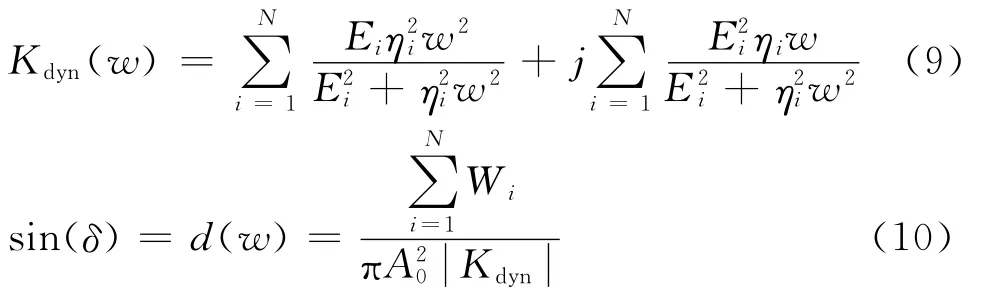
其中:Kdyn为黏弹单元总的动刚度;δ为黏弹单元的滞后角;d(w)为黏弹单元的阻尼系数。
当Ei=Kv,ηi=C时,一个黏弹单元在振幅为x0的简谐激励中,响应力的幅值为

响应力实部的值为
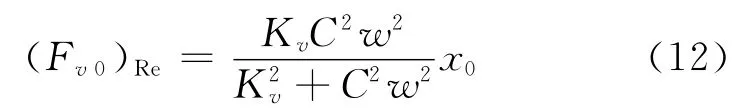
响应力虚部的值为

一个周期损耗的能量为

黏弹单元整体表现出的响应力为各Maxwell单元相加

其中:n为 Maxwell单元的个数;Fvi(x)为第i个Maxwell单元的响应力。
2.1.4 模型叠加
将弹性单元、摩擦单元与黏弹单元叠加,得到响应力和激励位移的关系为

其中:Fe(x)为弹性单元的力;Ff(x)为摩擦单元的力;Fv(x)为黏弹单元的力,为各黏弹单元响应力之和。
整体模型响应力的振幅为

一个循环中整体模型能量消耗为

对简谐振动而言,衬套轴向动刚度和阻尼系数可以通过下式确定

2.2 参数识别
2.2.1 弹性单元和摩擦单元参数识别
作激励力随激励位移的变化曲线,即滞回曲线,并确保滞回曲线的中心在零点位置,如图8所示。在位移接近极限位移时,曲线的斜率就近似表示该试件弹性单元的值,即其静态刚度值Ke。
延长接近极限位移处曲线的两条切线,由激励位移的对称性可知,两条切线平行,两条切线间的竖直距离就近似等于两倍的摩擦力的最大值。由此,确定摩擦单元的参数Ffmax。
根据试验结果,得到曲线的最大斜率值Kmax,见图8。摩擦单元的第2个参数x2由下式求得


图8 低频简谐激励下激励位移与响应力的关系Fig.8 The response force versus displacement of lowfrequency harmonic excitation
参数识别工况采用低频率大振幅工况,低频率是为了进一步减小频率的影响,大振幅是为了保证摩擦单元能够发挥出最大摩擦力。最终选择的参数识别工况为激励频率为4Hz,激励振幅为1.5mm,根据前面所述识别方法,识别结果如表3所示。

表3 弹性单元和摩擦单元参数识别结果Tab.3 The fitted parameters of elastic element and friction element
2.2.2 黏弹单元参数识别
在黏弹单元参数识别以前,首先要分析试验结果,确定将使用的黏弹单元的个数。根据试验结果,频率对阻尼系数的影响比对动刚度的影响要大些,所以将根据阻尼系数的变化规律,确定使用的黏弹单元的个数。阻尼系数试验结果如图4(c)所示。
可以发现,试验结果表现出两种变化规律:4Hz为一种;8,12,16,20Hz为另一种。这表明可以用两个黏弹单元来表示衬套模型的频率相关性。因此,将4Hz作为第1个黏弹单元的识别工况,将12Hz作为第2个黏弹单元的识别工况。识别方法是利用试验结果和仿真结果的相对误差最小化。使用Matlab中的优化函数fmincon求目标函数的最小值,目标函数如下
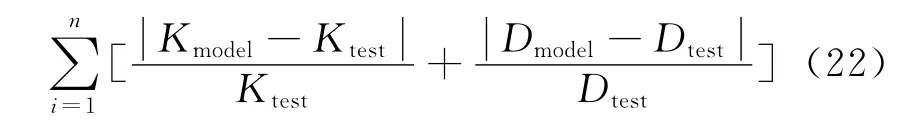
其中:n为试验工况的个数;Kmodel和Dmodel分别表示根据动态模型求得的在对应试验工况下的动刚度值和阻尼值;Ktest和Dtest表示试验得到的动刚度值和阻尼值。
黏弹单元参数识别结果见表4。

表4 黏弹单元参数识别结果Tab.4 The fitted parameters of visco-elastic elements
最终的新型衬套动态模型总共有7个待识别参数,分别是:弹性单元的刚度值Ke;两个黏弹单元的刚度值E1,E2;阻尼系数η1,η2;摩擦单元的最大摩擦力Ffmax及达到最大摩擦力一半时的位移x2。其示意图如图9所示。

图9 衬套轴向动态模型示意图Fig.9 The axial dynamic model of bushing
2.3 误差分析
模型仿真结果和试验结果比较如图10所示,试验结果和仿真结果的最大误差如表5所示。由试验结果和仿真结果的对比可知,试验结果和动态模型的仿真结果变化规律一致,误差也较小。动刚度的最大误差控制在6%以内,阻尼系数的最大误差控制在8%以内,精度较高。由此说明了此种建模方法和参数识别方法的合理性。

表5 同工况下动态特性最大误差值Tab.5 The maximum error of dynamic characteristics in same conditions
3 结 论
1)通过衬套试验,得到衬套轴向的静、动态特性。发现在低频段,橡胶衬套动刚度和阻尼系数随着振幅增大迅速降低,而随频率变化不明显。

图10 模型动态特性仿真与试验结果对比Fig.10 The dynamic characteristics comparison of simulation and test
2)提出一种将弹性单元、摩擦单元和若干黏弹单元叠加的新型橡胶衬套模型,该模型结构简单,物理意义明确。
3)根据试验结果和模型仿真结果的对比,该新型衬套模型可以准确描述衬套轴向的频率相关性和振幅相关性。证明笔者所提出的衬套轴向动态模型建立方法和参数识别方法正确可行。
4)该模型可通过用户子程序的形式应用到Adams等多体动力学软件的动力学仿真中,具有较高的实用价值。
[1] 张平,柴国钟,潘孝勇,等.橡胶隔振器静态特性计算方法研究[J].振动、测试与诊断,2010,30(2):105-110.
Zhang Ping,Chai Guozhong,Pan Xiaoyong,et al.Investigation on calculation method for the static characteristics of a rubber isolator[J].Journal of Vibration,Measurement & Diagnosis,2010,30(2):105-110.(in Chinese)
[2] 李军强,刘宏昭,王忠民.线性黏弹性本构方程及其动力学应用研究综述[J].振动与冲击,2005,24(2):116-121.
Li Junqiang,Liu Hongzhao,Wang Zhongmin.Review on the linear constitutive equation and its dynamics applications to viscoelastic materials[J].Journal of Vibration and Shock,2005,24(2):116-121.(in Chinese)
[3] 潘孝勇.橡胶隔振器动态特性计算与建模方法的研究[D].杭州:浙江工业大学,2009.
[4] 郭学良.面向电动轮悬架高频振动特性的橡胶衬套模型[D].上海:同济大学,2013.
[5] 潘孝勇,上官文斌,柴国钟,等.基于超弹性、分数导数和摩擦模型的碳黑填充橡胶隔振器动态建模[J].振动与冲击,2007,26(10):6-10.
Pan Xiaoyong,Shangguan Wenbin,Chai Guozhong,et al.Dynamic modeling for carbon-filled rubber isolators based on hyperelasticity,fractional derivative and a generalized frictional model[J].Journal of Vibration and Shock,2007,26(10):6-10.(in Chinese)
[6] 上官文斌,吕振华.汽车动力总成橡胶隔振器弹性特性的有限元分析[J].内燃机工程,2003(6):50-55.
Shangguan Wenbin,LüZhenhua.Finite element analysis of elastic characteristics of rubber isolator for automotive powertrain systems[J].Chinese Internal Combustion Engine Engneering,2003(6):50-55.(in Chinese)
[7] Rossilthin Y A,Shitikova M V.A new method for solving dynamic problems of fraetional derivative Viseoelastieity[J].Intemational Journal of Engineering Seienee,2001,39:149-176.
[8] 上官文斌.汽车悬架控制臂液压衬套动态特性实测与计算分析[J].振动与冲击,2007,26(9):7-10.
Shangguan Wenbin.Experment and calculation methods for analyzing dynamic performances of hydraulic bushings used in control arms of a suspension[J].Journal of Vibration and Shock,2007,26(9):7-10.(in Chinese)
[9] Berg M.A rubber spring model for dynamic analysis of rail vehicles[M].Stockholm:Kungl Tekniska Hogskolan,1995:23-25.
[10]Berg M.A model for rubber springs in the dynamic analysis of rail vehicles[J].Proceedings of Mechnical Engineers Part F:Journal of Rail and Rapid Transit,1997,211(2):95-108.
[11]Berg M.A non-linear rubber spring model for rail vehicle dynamics analysis[J].Vehicle System Dynamics,1998,30(3-4):197-212.

