变工况特性下的风电轴承早期故障诊断方法

王 珊，苏璐玮，顾煜炯，杨 昆

(华北电力大学 能源动力与机械工程学院，北京102206)

0 引言

滚动轴承是风电机组中重要部件。由于机组工作环境条件恶劣，温度湿度的影响以及由于风况的变化引起的轴承载荷变化使得轴承极易发生故障。对轴承的早期故障诊断及故障趋势预测可以尽早发现故障并安排检修，从而保证风电机组有效稳定运行。

西北工业大学廖明夫［1］对滚动轴承振动信号进行了自适应共振解调分析，提取轴承的故障信息。Randall R B［2］根据滚动轴承损伤性冲击故障的循环平稳特性，利用循环平稳解调成功地分离了齿轮和轴承故障。华北电力大学王晓龙［3］，针对电动机的滚动轴承故障问题，提出了基于EEMD 和Teager 能量算子解调的诊断新方法。浙江大学郭艳平［4］介绍了基于EMD 和散度指标的滚动轴承故障诊断新方法，通过计算故障特征量的J－散度和KL － 散度来判断故障类型和描述故障程度。

目前来看，共振解调方法是工程中常用的滚动轴承故障振动信号分析方法，但是该方法存在两个问题:(1)必须事先通过冲击试验来确定高频共振频率;(2)带通滤波器的中心频率和带宽固定不变。EMD 在轴承故障特征提取中的应用可自适应地提取故障冲击信号，避免了共振解调中心频率选择和多个固有频率共存的问题。但目前EMD 在风电机组轴承中的应用仍存在一些问题需要研究，对于变工况造成的频率成分变化问题和IMF 分量选取的问题。此背景下，本文提出基于角域信号IMF 分量优化选取的风电机组轴承早期故障诊断的方法，将阶比重采样后获得的角域信号进行EMD 分解，根据互相关系数准则和峭度准则选取包含故障信息的IMF 分量，再利用时频谱和边际谱提取故障特征，实现风电机组轴承的早期故障诊断。

1 风电轴承各故障发生阶段的特点

滚动轴承4 个阶段的频谱特征如下:

(1)噪声和温度正常，可用超声、振动尖峰能量声发射测量出来，振动总量较小，无离散的轴承故障频率尖峰。

(2)轻微的轴承故障，轴承工作噪声略增大，温度正常，开始出现轴承部件的固有频率，一般在500 ～2 000 Hz 范围内。本阶段中后期表现为在固有频率附近出现边频。

(3)可以听到噪声，温度略有升高，出现滚动轴承故障频率及其谐波频率。故障进一步扩展时，出现较多的滚动轴承故障频率的谐波频率，并且边带频率的数量增多。

(4)轴承工作时的噪声强度改变，温度明显升高，这一阶段影响1 倍频，并引起其他倍频分量的增大，轴承故障频率和固有频率开始消失被随机振动或噪声所代替［5］。

通过研究轴承各故障阶段的特点，由图1 发现在轴承发生早期故障时，振动信号是最先有所反应的。由于振动信号对于轴承早期故障的敏感性好，本文选用振动分析方法来进行轴承的早期故障诊断。

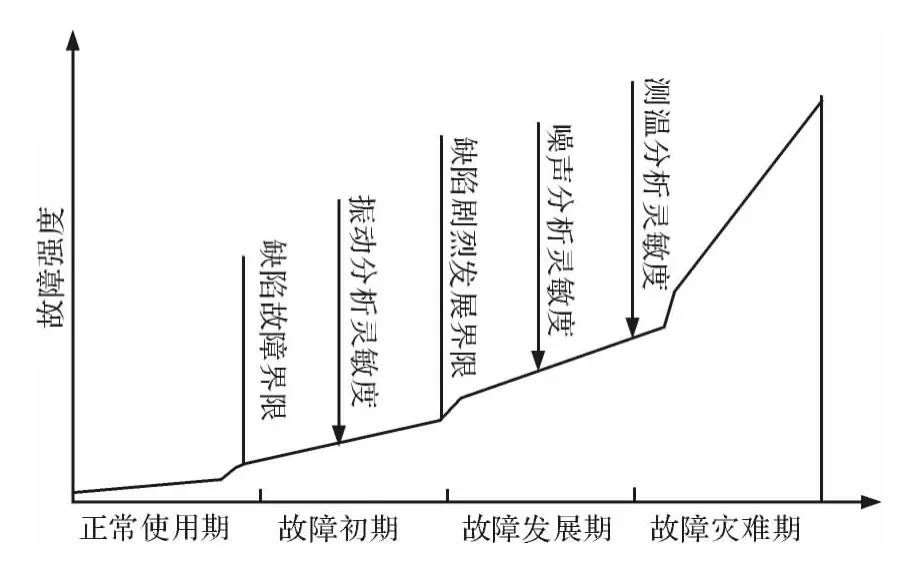
图1 轴承故障发生阶段及检测技术示意图

轴承故障的第一阶段故障信号表现不明显，虽然可以通过用超声、振动尖峰能量声发射测量出来，但是这是一个不能在线诊断的方法，且诊断精度也不能保证。根据第二阶段特点，局部故障产生的冲击振动会激起轴承系统各部件的高频固有振动，从而导致幅值调制现象，低频调制信号的频率与滚动轴承发生局部故障的类型有关，因此，只要能够找出低频调制的频率就可以判断出轴承哪一部件发生了故障。

2 基于二次曲线拟合的阶比重采样

变速恒频风力发电机的转速一直随风速变化，采集到的振动信号中主要的频率成分受转速的影响而不断发生变化。传统的频谱分析方法对非平稳信号进行分析时会产生明显的频率混叠现象。为了更好地对旋转机械的非平稳信号进行分析，揭示其频率随时间变化的规律，提出阶比分析技术来准确的提取故障频率［6］。

传统的阶比分析方法有硬件阶比跟踪技术和计算阶比跟踪技术，硬件阶比跟踪技术会受到现场安装条件的限制且需要昂贵的相关设备，也不利于虚拟仪器的开发。而现有的计算跟踪技术也存在一些问题，或者精度不高，或者计算效率低。在总结了现有计算阶比跟踪技术的基础上，本文提出二次曲线拟合的计算阶比重采样。其基本思想是假定转子在短时间内(至少连续3 个脉冲间隔)是匀角加速运动，根据已知的3 个脉冲时刻值，求出二次曲线的系数，得到二次曲线方程，进而得到阶比重采样时刻，最后根据重采样时刻对原始振动信号重采样，得到准平稳的角域信号。

通常，为了确定重采样的时间点首先要计算等角度发生的时刻序列，假设转子在短时间内是匀角加速度运动，转过的角度θ可表示为:

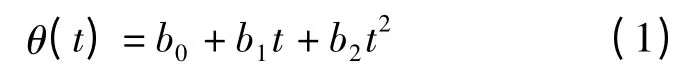
式中:b0，b1，b2为待定系数;已知连续3 个脉冲的到达时刻值t1，t2，t3。设定两个脉冲之间转过的角度为

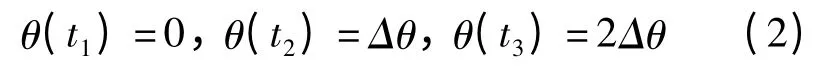
将式(2)代入式(1)中求解系数b0，b1，b2，可得任意转角下θ所对应的时刻t，则重采样时刻的基本计算公式为

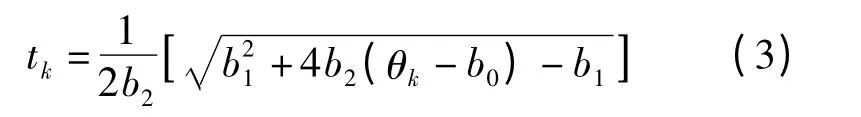
式中:tk是转过角位置为θk时所对应的时间。

通过二次曲线拟合计算阶比重采样时刻的方法，可适用于转速变化较大或精度要求较高的场合，本文中使用的二次曲线拟合方法满足精度要求。

3 风电机组轴承早期故障诊断

3.1 角域信号IMF 分量优化选取

经验模式分解的主要思想是把一个时间序列的信号分解为不同尺度的基本模式分量，它是由美国学者Huang［7］于1998 年首次提出的。通过把一个时间序列的信号经过EMD，分解为一组IMF分量，然后把某些有用的IMF 分量进行组合，便可构成高通、低通、带通滤波器。但是多数的降噪应用都是将EMD 得到的高频分量作为噪声直接去除，很多情况下有可能将有用的信号成分去除。对滚动轴承而言，与故障有关的冲击信号通常都处于较高频率段，所以上述方法对滚动轴承降噪行不通，因此有必要对EMD 降噪准则进行讨论。本文结合前人的研究成果及滚动轴承故障信号具有冲击的特征，提出了两条降噪准则。

准则1:互相关系数准则

由于插值误差、边界效应以及过分解等原因，在EMD 分解中常会出现伪分量，即与原始信号无关的分量，这些伪分量所含有的频率成分存在与特征频带重合的可能，所以应该采取办法将其辨别出来，予以剔除。文献［8］中提出了一种基于互相关的伪分量判定方法，通过IMF 与原始信号之间的互相关系数来判定IMF 的真伪:各IMF 与原信号的相关性约等于各IMF 的自相关;而伪分量与原信号的相关性很小。因此，从分解后各IMF 与原信号的相关性分析中，可以看出各IMF 的真伪。

定义分解出的各IMF 与原信号的互相关系数为:

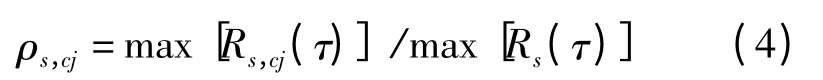
式中:Rs，cj(τ)为各IMF 与原始信号的互相关;Rs(τ)为原始信号的自相关。把分解后各IMF与原信号的相关系数的大小作为评定各IMF 是否为伪分量的指标。

准则2:峭度指标准则

峭度指标是描述波形尖峰度的一个无量纲参数，峭度指标K的定义为:

式中:μ为信号x的均值;σ为信号x的标准差。

当信号近似服从正态分布时，其峭度指标约为3，而当信号存在较多冲击成分时，峭度指标明显增大。当滚动轴承正常运转时，其振动信号的幅值分布接近于正态分布，因此其峭度指标约等于3。当滚动轴承发生局部故障时，由故障引起的冲击振动信号明显偏离正态分布，且峭度指标越大说明信号中冲击成分所占的比重越多，而滚动轴承故障信息往往包含于这些冲击成分较多的幅值调制信号中。当某些IMF 的峭度指标大于3 时，说明这些IMF 中含有较多的冲击成分，即原信号分解后较多的故障冲击成分保留在这些IMF 中。对这些IMF 进行重构，得到的合成信号其峭度指标有着明显的提高，故障越明显，提高程度越大。

3.2 Hilbert 的时频谱和边际谱

对EMD 分解后得到的本征模态函数ci(t)进行Hilbert 变换，可以获得Hilbert 时频谱和边际谱，算法如下［9］:

(1)进行Hilbert 变换

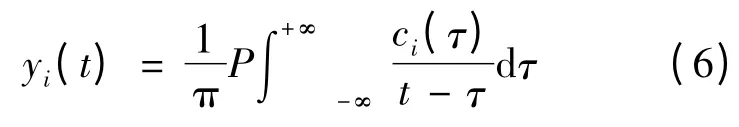
(2)构造解析函数

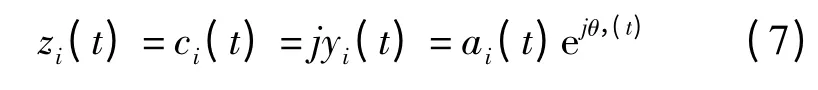
其中

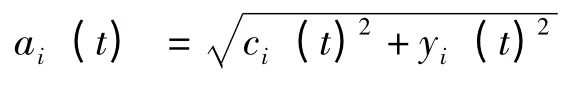
式中:

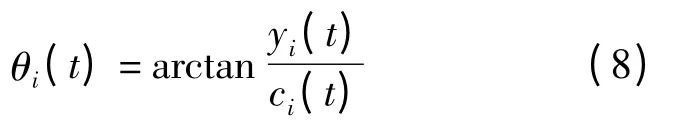
θi(t)和ai(t)分别为顺时振幅和相位。

(3)瞬时频率

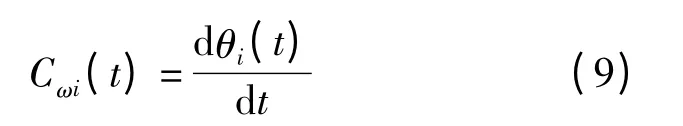
(4)定义Hilbert 幅值谱H(ω，t)为

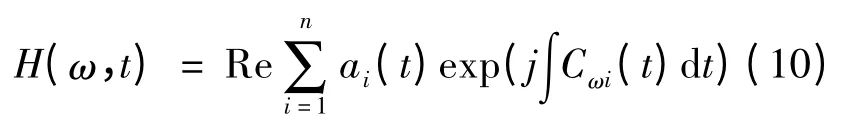
(5)根据幅值谱可以得Hilbert 边际谱

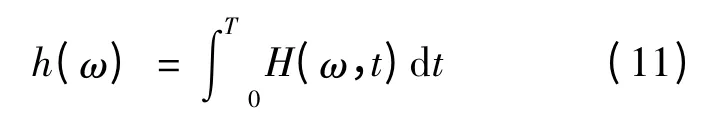
4 故障特征提取及诊断方法

4.1 故障特征提取

信号的边际谱，反映了周期性的故障特征冲击成分及其剧烈程度，这时需要一个合适的指标，来准确描述轴承的工作状况和故障类型。当轴承分别在内圈、外圈和滚动体部位出现故障时，在边际谱中相应的故障阶次处会出现峰值，所以选取能表征故障类型的故障特征频率(依次表示fo，fi，fr)处的幅值为特征量，表示为M= ［Afo，Afi，Afr］。通过处理实测振动数据计算得出各个故障位置下的标准特征量，外圈，内圈和滚动体故障的标准特征量分别为Mo，Mi，Mr。计算实时的特征量和Mo，Mi，Mr的马氏距离即可判断故障位置。

4.2 诊断方法

通过上述分析，利用基于角域信号IMF 分量优化选取的提取滚动轴承早期故障信息可以总结为以下几个步骤:

(1)对采集的振动信号进行等角域重采样，转化为角域稳态信号。

(2)对角域信号进行EMD 分解，得到一组IMF 分量。

(3)计算各IMF 与原信号的互相关系数。

(4)计算各IMF 的峭度指标。

(5)取互相关系数和峭度指标均较大时对应的IMF，将这些IMF 相加，重构得到合成信号。

(6)对重构信号进行Hilbert 变换，可以获得Hilbert 边际谱，根据边际谱中的故障特征频率可以得出特征矩阵，计算实时的特征量和Mo，Mi，Mr的马氏距离即可判断故障位置。

5 案例应用

本文在风力发电机组实验台上进行了轴承故障实验，实验台(如图2 所示)主要由调速电机、齿轮箱与发电机组成，利用调速电机控制转子转速模拟变工况状态。轴承座上装有加速度传感器，用来采集轴承的振动加速度信号，采样频率为8 192 Hz。采样点数为16 384 个。发电机轴承为圆柱滚子轴承，轴承型号为NJ2326，其内环故障特征频率fi=8.379 4fn;外环故障特征频率fo=5.652 2fn;滚动体故障特征频率fr=4.980 2fn;fn为齿轮箱高速轴的旋转频率。试验时将转子由800 r/min 加速到1 200 r/min。通过线切割的方式在外圈开浅槽来模拟轴承外圈早期故障，为验证该方法对浅槽深度的要求，固定浅槽宽度为0.2 mm，试验参数设定如表1 所示。

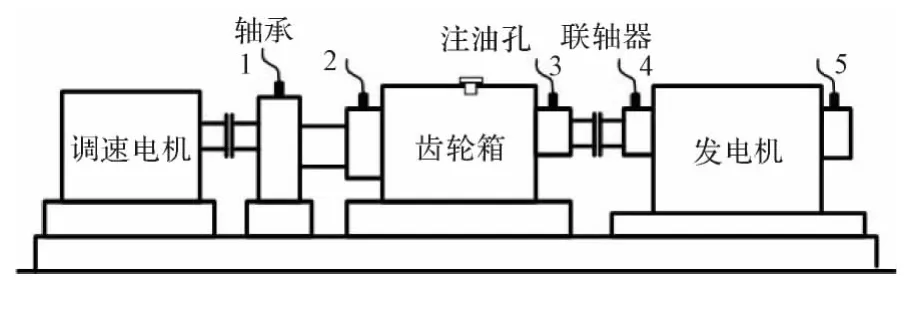
图2 风电机组故障模拟试验台

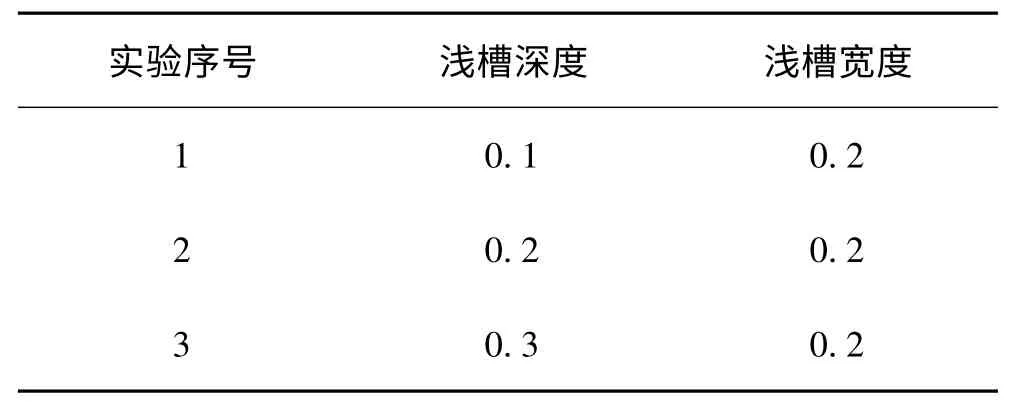
表1 试验参数设定 mm

以第三组实验为例介绍本文的实验处理方法，图3 是原始信号时域图，槽深为0.3 mm。由图中可以看出:信号的幅值随着输入轴转速的升高而逐渐增大，说明齿轮箱的振动信号与输入轴的转速有直接的关系。同时，该信号为一个非平稳的过程信号，信号中包含的频率随转速的不断变化，需要对其进行角域重采样转化成角域的准平稳信号。图3 中下图是对原始振动信号进行角域重采样后的信号，与图3 中上图的原始时域信号相比，其稳定性已大为改善。

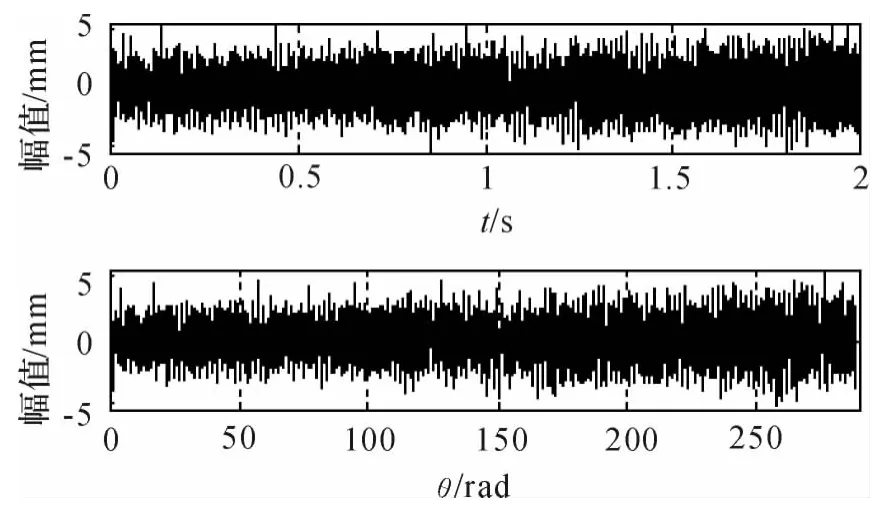
图3 2s 样本数据的时域波形及角域波形

图4 是对重采样后的角域信号进行的EMD 分解图，槽深为0.3 mm。按照从高频到低频的顺序排列。计算各IMF 与原信号的互相关系数及各自峭度指标如表2 所示。

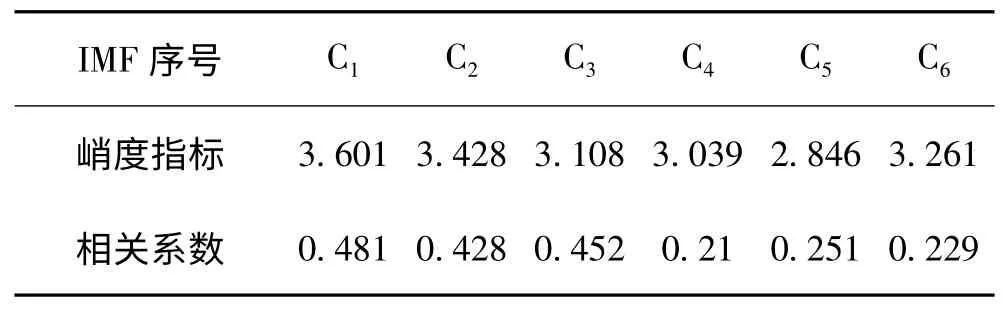
表2 各IMF 与原信号的互相关系数及各自峭度指标

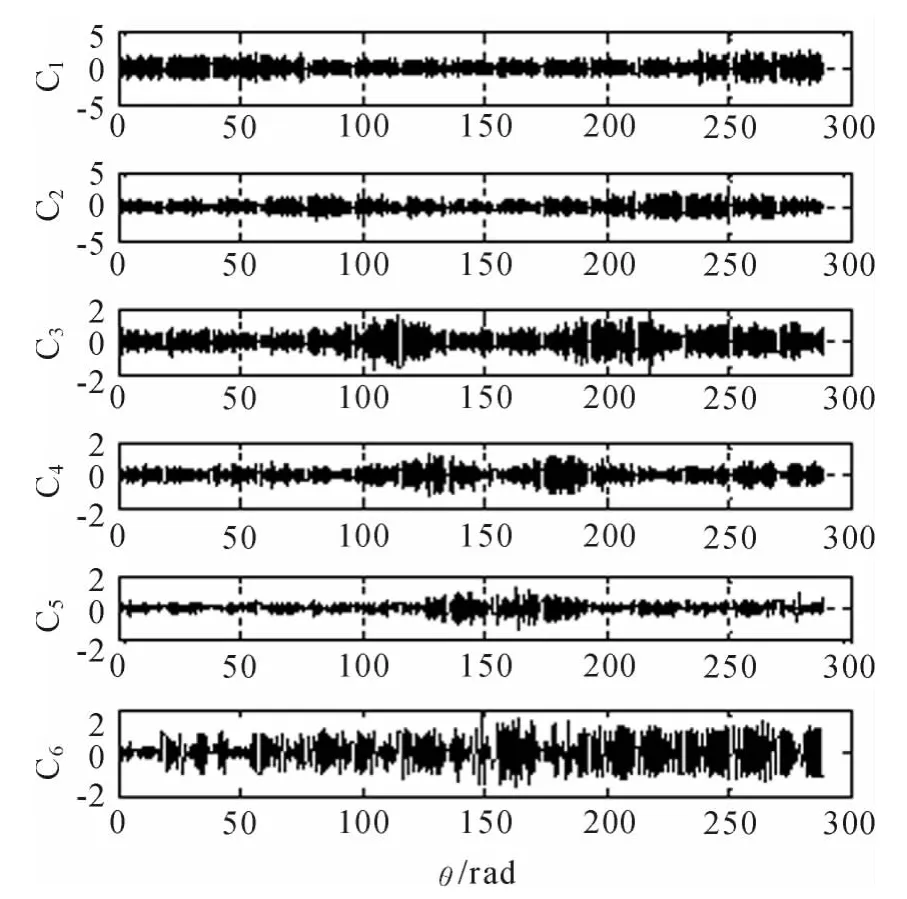
图4 角域信号的EMD 分解图

由表2 可以得出C1，C2，C3的峭度指标大于3 且相关系数较大，提取这3 个IMF 分量重构信号，图5 是重构后的角域信号，槽深为0.3 mm，图中可以看出，时域波形冲击成分更明显，保留了高频共振成分，也减少了低频干扰的影响。

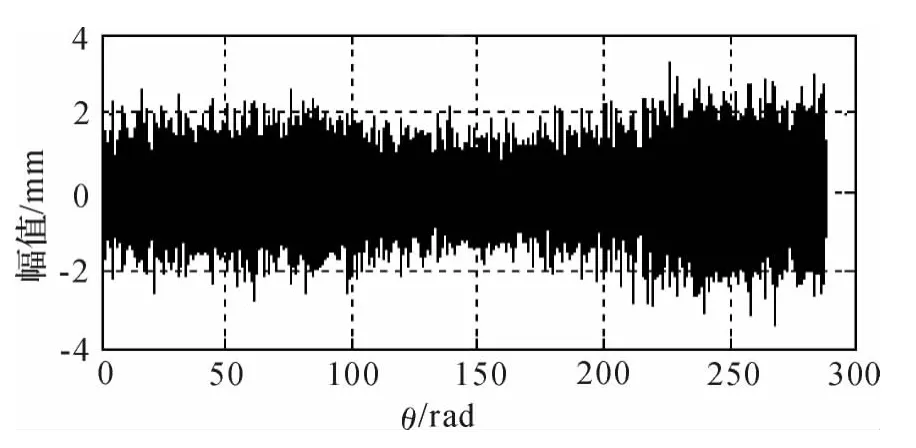
图5 重构信号的角域波形

对重构信号进行Hilbert 变换获得图6 的Hilbert 边际谱，Hilbert 边际谱可以看出信号的幅值随阶比的变化情况，根据边际谱获得待检样本特征矩阵为M1=(5.652 2，0.375 1，0.156 8)，分别计算M1和Mo，Mi，Mr的马氏距离为do=0.256，di=5.278，dr=4.954，其中do最小，因此可以判断该轴承外圈存在早期故障。图6 中槽深为0.3 mm。

而试验1 和2 中由于浅槽深度较浅，从边际谱图中不能检测出故障频率，如图7 和8 所示。故得出结论:本文提出的中风电机组的轴承早期故障诊断方法对轴承损伤的浅槽深度要求为0.3 mm。

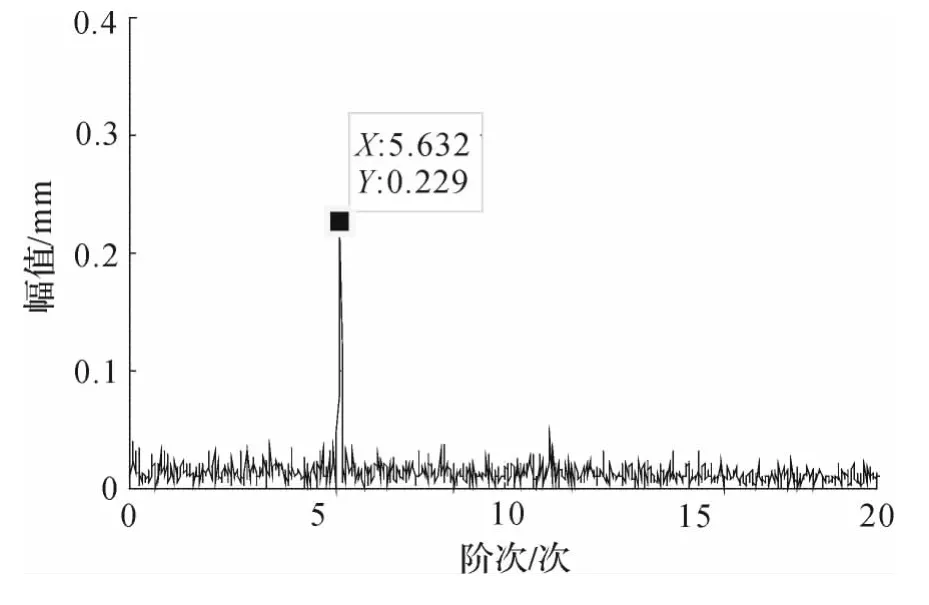
图6 重构信号边际谱

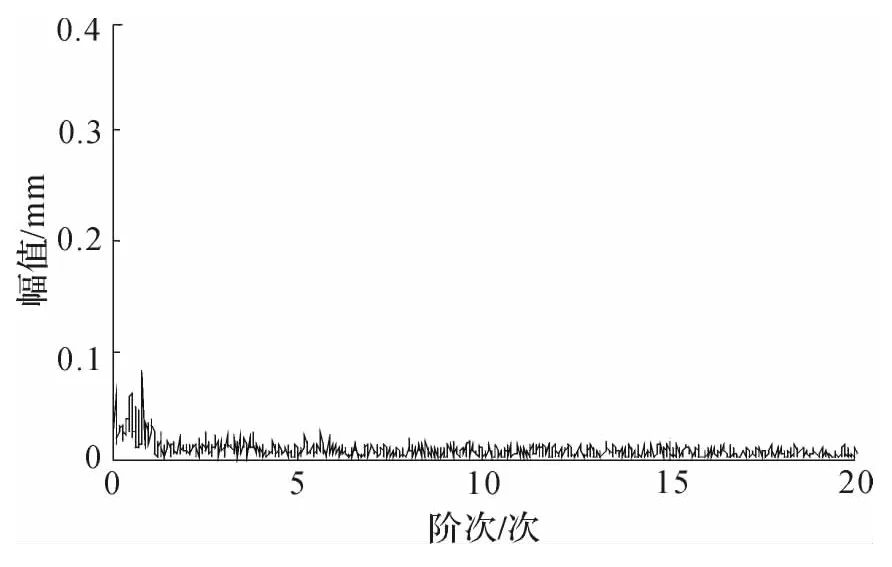
图7 重构信号边际谱(槽深=0.1 mm)

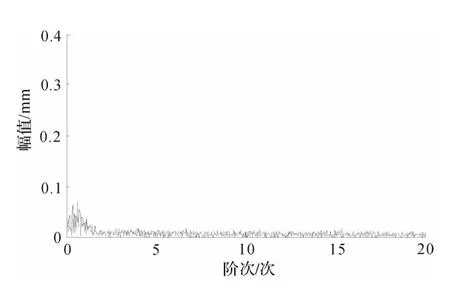
图8 重构信号边际谱(槽深=0.2 mm)

6 结论

(1)风力发电机轴承在变工况环境下工作，利用阶比分析方法能够解决传统的频谱分析法难以克服的“频率模糊”现象，将时域里的非平稳信号转换为角域里的准平稳信号。

(2)结合互相关系数准则和峭度指标准则的EMD 降噪，提取出了含有故障信息的IMF 分量，可以突出信号高频共振成分，减少低频干扰。

(3)在边际谱中呈现的特征量与轴承状态之间存在密切联系，用HHT 方法分析滚动轴承故障振动信号，能够得到很好的诊断结果。

(4)本文提出的轴承早期故障诊断的方法对轴承损伤的浅槽深度要求为0.3 mm。浅槽深度低于0.3 mm 的轴承局部损伤难以检测。

［1］王平，廖明夫．滚动轴承故障诊断的自适应共振解调技 术［J］．航 空 动 力 学 报，2005，20 (4):606-612．

［2］Randall R B．Detection and diagnosis of incipient bearing failure in helicopter gearboxes［J］．Engineering Failure Analysis，2004，11 (2):177-190．

［3］王晓龙．基于EEMD 和Teager 能量算子解调的故障诊断研究［J］．电力科学与工程，2013，29 (3):18-22．

［4］郭艳平，颜文俊，包哲静，等．基于经验模态分解和散度指标的风力发电机滚动轴承故障诊断方法［J］．电力系统保护与控制，2012，40 (17):83-87．

［5］毛亚红，刘金良．振动分析技术在风机滚动轴承故障诊断中的应用［J］．中国设备工程，2011，35 (6):57-59．

［6］郭瑜，秦树人．基于瞬时频率估计及时频滤波的阶比分量提取［J］．中国机械工程，2003，14 (17):1506-1509．

［7］Huang N E，Shen Z，Long S R，et al．The empirical mode decomposition and the Hilbert spectrum for nonlinear and non － stationary time series analysis ［J］．Proceedings of the Royal Society of London．Series A:Mathematical，Physical and Engineering Sciences，1998，454(1971):903-995．

［8］胡红英，马孝江．基于局域波分解的信号降噪算法［J］．农业机械学报，2009，37 (1):118-120．

［9］于德介，程军圣，杨宇．机械故障诊断的Hilbert-Huang 变换方法［M］．北京:科学出版社，2006．