基于粒子群优化的选择性催化还原脱硝控制系统仿真

王 瑾，董 泽

(华北电力大学 控制与计算机工程学院，河北 保定071003)

0 引言

煤炭作为重要的能源资源，在目前乃至以后很长一段时间，在能源结构中占据主要位置。煤炭的主要消耗方式为燃烧，占了约70%，其中，燃煤电站是煤炭燃烧的主要消耗方，燃煤锅炉燃烧煤炭产生大量烟气，烟气中的NOx是人为NOx源的主要来源之一。根据最新排放标准GB 13223－2003 《火电厂大气污染物排放标准》中对电站NOx排放的规定［1］，2004 年后燃煤电站的NOx最高允许排放浓度为450 ～650 mg/m3。而目前，中国的NOx年排放量仅次于美国，年排放量保持在1 000 万t 级的水平之上［2］，且中国在控制NOx排放的技术上还远远落后于先进国家，因此，了解燃煤电站NOx的现状，掌握其产生的激励，实现NOx排放的有效控制，是落实节能减排任务的重中之重。氮氧化物是形成区域细粒子污染和灰霾的重要原因，也是生成臭氧造成全球气候变暖的重要前体物之一，会对人体造成较大的健康威胁，并对水生和陆地的生态系统造成破坏，火电厂排放烟气中的污染物，需要集中控制的为SO2，NOx和烟尘，其中，NOx主要包括NO，NO2，以及少量的N2O 等，其中NO 占90%，NO2占5% ～10%，N2O 占大约1%，因此燃煤电站NOx的生成与排放量主要取决于NO。

1 SCR 法脱硝基本原理

选择性催化还原技术(selective catalytic reduction，SCR)是目前应用最广泛、技术最成熟的烟气脱硝技术之一，其原理是利用喷射NH3与催化剂(铁、钒、铬、钴等金属)在温度为200 ～450 ℃时将NOx还原为N2。主要反应式如下［1］:

其中，NH3，CO，H2，甲烷、乙烯、丙烷、丙烯等都可作为反应的催化剂，反应时，烟气中的NOx和注入的NH3几乎以等摩尔比进行反应，可以得到80% ～90%以上的脱销效率。SCR 脱销基本反应原理如图1 所示［3］。

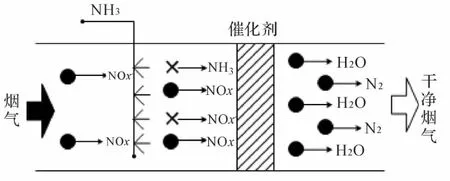
图1 SCR 脱硝反应原理

2 SCR 脱硝系统

2.1 SCR 脱销系统组成

烟气脱硝系统由还原剂制备系统和脱硝反应系统两部分组成，脱硝反应系统包括稀释空气供应系统、SCR 催化反应器、喷氨系统。液氨存储和供应系统包括液氨卸料压缩机、液氨储槽、液氨蒸发槽、氨气缓冲槽和氨气稀释槽、废水泵和废水池［4］等。典型的SCR 工艺流程主要包含以下几个步骤:

(1)氨的制备与储存;

(2)氨的蒸发及与预混空气相混合;

(3)氨与空气充分混合后，在反应器的适当位置喷入烟气系统，其位置常在反应器入口附近的烟气管路内;

(4)喷入的混合气体与烟气的混合;

(5)各反应物向催化剂表面的扩散并进行反应。

2.2 SCR 脱销系统的工艺布置

电厂SCR 反应器一般选用高温高尘段布置工艺［5］，将反应器布置在省煤器的下游、空气预热器和除尘器的上游，其优点是进入的烟气温度较高，可到达280 ～420 ℃，催化剂在这个温度范围内有较高的催化活性，烟气不需要进行再热即可取得良好的脱硝效果。工艺布置图如图2 所示。

图2 SCR 工艺系统布置图

3 SCR 脱硝控制系统

SCR 脱硝法氨逃逸率较小，脱氨效率可高达90% 以上，为了使SCR 脱氨系统可以连续、可靠、有效地运行，需要设计一个性能良好的自动控制系统。在SCR 脱硝控制中，最重要的运行参数是烟气流速、烟气温度、SO3浓度、氧气浓度、氨逃逸量、水蒸气浓度等，根据工艺特点和流程，主要的模拟量调节包括了SCR 反应器氨气流量控制、液氨蒸发槽温度控制、氨气缓冲槽压力控制等，其中模拟量调节系统的核心控制为SCR 反应器氨气流量控制。

3.1 氨气流量及出口NOx 浓度的控制

由于氨气脱硝是一个迟延过程，在实行脱硝控制策略前首先要考虑以下问题:(1)NOx测量信号存在较大的滞后;(2)NOx在催化剂作用下的时间复杂性;(3)氨气逃逸率控制。综合考虑以上问题，提出了出口NOx定值控制方式。该控制方式控制反应器NOx为定值，较常规方法更容易监视，同时氨气损耗量更小。SCR 烟气脱硝系统测量入口和出口的NOx浓度进行处理，得到预置摩尔比并计算出所需的NH3流量，其控制原理如图3。

图3 SCR 变摩尔比控制原理图

测得的脱硝反应器入口NOx浓度信号与烟气流量相乘得到NOx流量信号，与预置的摩尔比相乘即得到所需的氨气流量，将氨气流量信号作为测量值送入PID 控制器，同时，经过氨气压力、温度信号修正的氨气流量设定值也被送入PID 控制器，通过计算出的氨气需求量信号调节喷氨控制阀的开度。由此实现了氨气脱硝的自动控制。

SCR 出口NOx定值控制方式为双回路控制系统，由于系统具有反馈滞后与响应滞后，氨气流量控制回路引入设定负荷与实际负荷偏差作为前馈，当负荷有较大波动时可提前喷射氨气，增强控制系统调节的及时性。出口NOx浓度控制回路中，利用入口NOx浓度实际测量值与出口NOx设定值计算预脱氨效率和预置摩尔比，预置摩尔比作为摩尔比控制器的输出基准，出口NOx浓度测量值和出口NOx设定值进行比较后经过PID 控制器输出，其输出作为修正量，最终得到系统目前需要的摩尔比。该摩尔比信号作为摩尔比设定值，控制氨的流量，保证出口NOx稳定在设定值上。

3.2 加热蒸汽温度和液氨压力的控制

加热蒸汽温度选用单回路控制，脱氨系统运行后，调节蒸汽进口阀开度将氨气出口温度控制在30 ℃左右。液氨出口压力控制也为单回路控制，通过调节蒸发器氨液入口阀控制氨气出口压力。由于实际工况中，负荷变化时氨流量变化大，在控制回路中加入流量指令信号作为前馈，以实现优先调节压力，保证系统稳定性的作用，完善其后的氨流量控制。

4 SCR 脱硝控制系统的优化及调试

控制对象的传递函数选择国华三河电厂二期2 ×300 MW 机组的参数［6］，其中，氨气流量响应函数Fcn1 = 4. 11/(16s2+ 2s+ 1)，出口NOx浓度响应函数Fcn2 = －1. 7e－13s(10 230s2+196s+1)－1。

4.1 粒子群(PSO)算法的基本原理

PSO 的基本思想是把每个优化问题的解看成搜索空间中的粒子，每个粒子都具有优化函数决定的适应值(Fitness Value)和一个速度向量决定其飞翔的方向和距离。PSO 首先对一群随机粒子进行初始化(初始速度、位移及其决定的适应值随机化)，然后迭代搜索最优解。每个迭代过程中，粒子跟踪两个最优值来更新自己的坐标，第一个就是当前时刻粒子本身所找到的最优解Xbesti，即个体最优值。另一个最优值是整个种群目前找到的最优解Xbestg，即全局最优解［7］。

假设在一个N维的目标搜索空间中(N代表Q(x)中未知因子个数，即优化参数)，有m个粒子组成的一个群体(m组可能解)，其中第i个粒子的位置表示为向量xi= (xi1，xi2，…，xiN)，其速度也是一个N维的向量，记为Vi= (vi1，vi2，…，viN)。随机产生一组Xi，作为第一代初始种群，将Xi代入目标函数Q(xi)即可计算出其适应值，适应值的大小衡量Xi的优劣。设粒子i迄今经历的最优位置记为Xbesti= (xi1，xi2，…xiN)，相应的适应值记为Qbesti，则粒子i的当前最好位置可表示为［8］:

搜索过程中粒子群经历的最优位置记为Xbestg= (xg1，xg2，…，xgN)，其对应的适应值即为全局最优解记为Qbestg。粒子根据式(1)更新自己的速度:

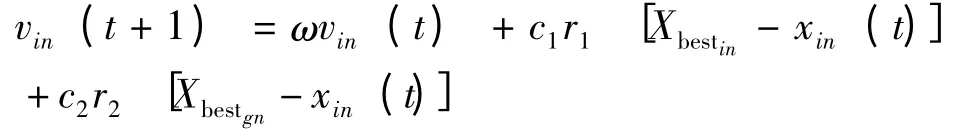
其中:i=1，2，…，m，n=1，2，…，N，t代表第t代，c1，c2为认知因子和社会因子，r1，r2为0 ～1 之间的随机变量，ω为惯性权重，平衡全局搜索和局部搜索。然后按式(3)来确定新的位置:

这样迭代下去直至达到要求得到最优值。

4.2 PSO 优化算法的设计

在实际应用中，粒子群算法是一种较好的全局优化算法，但它不能完全保证所得解的可行性和最优性，因此要求比较准确地优化上限与下限及参数的设计。由Matlab/Simulink 对该系统进行串级控制仿真，得到主副PID 参数，控制结果如图4 所示，由此确定优化变量的上下限为优化变量速度限制为:Vmax= ［0.5，5，0.1，5］;粒子个数和进化代数均选择10，惯性权重区间为［0.8 1.2］。程序见附录，得到的优化结果如图5 所示。

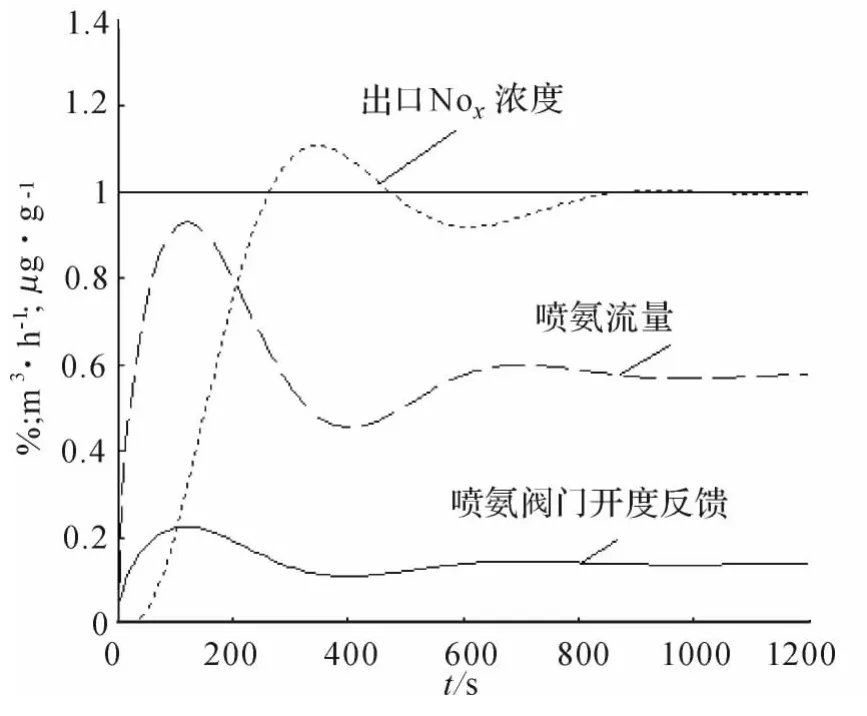
图4 基于串级PID 的SCR 脱硝控制曲线

图5 基于PSO 优化的SCR 脱硝控制结果

由结果可知，当出口NOx浓度上升时，串级PID 经过16 min 控制出口NOx浓度维持在稳定值，喷氨流量超调较大，不能很好地抑制内扰，PSO优化控制算法经过10 min 控制出口NOx浓度维持在稳定值，超调量控制在20%以内，喷氨流量能在较快时间内做出反应，阀门开度反馈的变化也在执行机构可接受的范围内。内扰是由于模型内部的迟延惯性导致的，而PSO 算法是基于系统状态进行搜索迭代，得到最优解，并不是基于模型，因此内扰出现时可不受模型约束，快速消除内扰。与串级PID 控制相比，该优化算法能更快地进行响应、使系统稳定。

5 结论

SCR 出口NOx定值控制策略比常规方法更容易进行监视，且有效地节省氨气的使用量。PSO算法能够很好地对控制对象进行优化，能比串级PID 控制更好地抑制内扰，减少对执行机构的损耗，节省氨气，使系统能够更快地稳定在设定值，从而达到更好的控制效果。

［1］中国大唐集团科技工程有限公司. 燃煤电站SCR 烟气脱硝工程技术［M］. 北京:中国电力出版社，2009．

［2］朱国容，解永刚．SCR 技术应用于国内大型燃煤电站锅炉的技术探讨［J］. 电站系统工程，2005，21(3):39-40.

［3］贾双燕，路涛，李晓芸. 选择性催化还原烟气脱硝技术及其在我国的应用研究［J］. 电力环境保护，2004，20 (1):19-21.

［4］钟秦. 燃煤烟气脱硫脱硝技术及工程实例［M］. 北京:化学工业出版社，2002．

［5］管一明，胡宇峰. 火电厂高飞灰布置SCR 系统的主要组成和设备［J］. 电力环境保护，2004，20 (4):25-27.

［6］李峰，王立，高富春. SCR 烟气脱硝自动控制系统及其在国华三河电厂的应用［J］. 热力发电，2009，38(5):91-93.

［7］韩璞，董泽，王东风，等. 智能控制理论及应用［M］. 北京:中国电力出版社，2012．

［8］魏星，崔鹏程. 粒子群优化算法及其在电力系统中的应用［J］. 电力科学与工程，2005，(3):21-24．