基于径向基函数的散乱点云孔洞修复算法

晏海平，吴禄慎，陈华伟

（南昌大学机电工程学院，江西南昌330031）

0 引 言

近年来，随着计算机技术的飞速发展，逆向工程技术在实物造型、模具缺陷检测与快速化修复、等诸多领域得到了广泛应用。在获取三维点云数据的过程中，由于模型本身损坏、激光扫描中的视线遮挡等原因，不可避免的会出现部分点云的缺失，而点云缺失直接影响后续建模的质量，因此在对散乱点云进行建模之前，需要先进行孔洞修复。许多专家学者对点云孔洞修复技术进行了大量的研究，目前在逆向工程领域的孔洞修补方法主要有两类:一类是以三角网格为基础对网格曲面孔洞进行修补［1－4］，该类算法在点云分布比较均匀和数据量较小时，能够获取较好的修补效果，但当点云数据量较大时，由于建立三角网格所需时间较多，难以取得理想的效果；另一类以散乱点云为基础的孔洞修复，文献［5］采用以孔洞边界点和边界周围的局部散乱点为依据建立曲面片，并在曲面片上进行采样的方法修复孔洞，修补精度较高，适合于曲率变化不大的曲面。文献［6］通过构建kd－tree提取点云的孔洞边界，并通过基于径向基函数的差值曲面实现残缺点云修补，但逼近二次曲面点列的误差难以控制。

本文在分析和研究已有算法的基础上，提出了一种先在孔洞多边形二维特征平面内进行点的填充，然后将填充点向基于径向基函数的隐式曲面上调整的方法实现孔洞的修复，并通过实验进行有效性验证。

在春季，在养殖业的过程中，鸡容易产生多种疾病。在育种过程中，只有仔细观察才能做出更好的判断和分析育种者用它做出更好的判断疾病的处理。否则，它会影响鸡的正常繁殖，并在同一时间，它会影响养鸡业的经济效益。因此，只有通过正确的判断和分析，才能采取更加针对性的预防措施来减少养殖户的损失。

1 散乱点云孔洞修补流程

本文主要对散乱点云的孔洞修复技术进行研究，算法流程如图1所示。

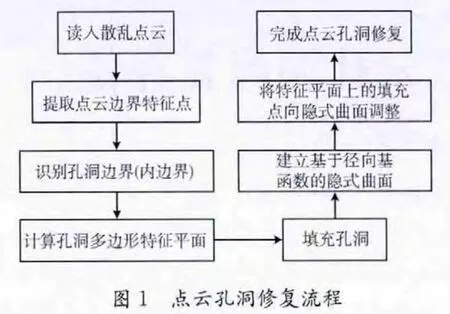
2 基于特征平面的点云孔洞填充

2.1 孔洞边界点的获取

采用文献［7］的方法建立散乱点云的空间拓补关系，计算出每个散乱点S的K邻域点集Ti（i＝0，1，…k－1），然后以散乱点及其K邻域作为局部型面参考依据建立基准平面，根据目标点到该平面的距离与点集中各点到该平面的距离比值大小［8］识别点云孔洞特征点，连接边界点得到边界线。

本试验通过对69批牡丹皮药材样品进行分析，并推测鉴定出29个共有峰的对应成分，主要是单萜苷类、酚酸类及黄酮类成分，这些共有成分可作为对牡丹皮药材进行质量控制的重要指标。

2.2 内外边界的识别

以上得到的边界线可能是封闭模型的内边界（孔洞边界），也可能是非封闭模型的外边界，在进行孔洞修补之前，首先就要识别出孔洞边界。

采用基于局部扩张的思想填充孔洞，新增填充点与孔洞边界能够实现较好过渡，主要过程如下:

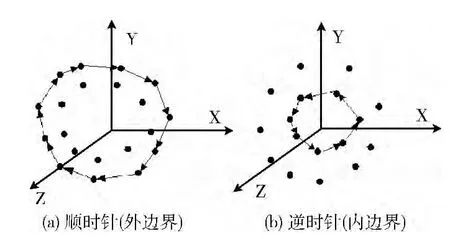
图2 识别内外边界

2.3 孔洞多边形的预处理

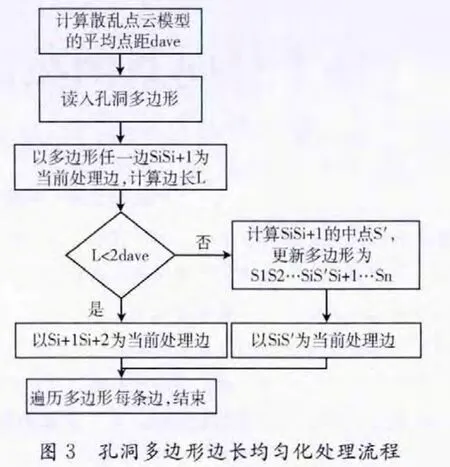
由于得到的孔洞多边形每条边的长度可能不均匀，影响后续处理效果。因此对孔洞多边形进行均匀化处理，主要步骤如图3所示。

德国前总理格哈德·施罗德说，习近平主席是一位远见卓识的改革家。他把马克思主义原理与中国实际结合，紧随时代进行创新，提出了雄心勃勃的改革计划，涵盖了各个领域。实践证明行之有效，深得人心，是实现中国梦的基本方略，也是开辟人类更加美好未来的行动指南。巴西中国问题研究所所长罗尼·林斯认为，中国共产党不仅能独立自主有效地治理自己的国家，而且将以更加积极的姿态参与全球治理。

2.4 填充孔洞

定义 边界线的特征平面:假设S1S2…Sn是散乱点集的边界线，应用最小二乘法拟合微切平面，计算该平面的法矢n和形心O，那么由n和O定义的平面为该边界线的特征平面N。将边界点S1S2…Sn和它们的邻域点投影到平面N上，以法矢方向为Z方向，规定遍历投影边界点时其邻域点在边界点的右侧，如图2所示，沿Z轴负方向看，当遍历投影边界点为顺时针时，则该边界为外边界；反之为内边界［9］。

上帝呀，如果我有一段生命……我不会放过哪怕是一天，而不对我所爱的人说我爱他们。我会使每个男人和女人都了解他们皆我所爱，我要怀着爱而生活。

采用以上算法对于平坦区域的孔洞进行填充效果较好，但由于孔洞新增点在特征平面上，对于曲率变化较大的模型孔洞填充后不能满足复杂形状要求，因此需要对这些填充点进行进一步的处理借鉴文献［10］的思路，本文以孔洞边界点及其邻域信息为基础，建立基于径向基函数的隐式曲面。对于R3空间中散乱点云的可以这样定义，给定n个空间散乱点｛q1q2…qn｝，且分别对应约束值｛h1h2…hn｝，如果能构造函数f（r）使得每个点均满足等式F（qi）＝hi，那么方程F（qi）＝0就可以表示一个隐式曲面。一般在定义一个隐式曲面时，该曲面要求通过的散乱点称为插值约束点和没有通过的点称为附件约束点，表达式如式下所示

步骤1 计算孔洞多边形的特征平面，将孔洞多边形向该平面投影，得到投影孔洞边界S′1S′2…S′i－1S′i＋1…S′n。

步骤2 计算投影边界相邻边的夹角β，将所有的多边形夹角进行升序排序。

步骤3 根据夹角βMin的大小进行处理，如果βMin＜90°，则不需要添加新的点，直接更新多边形为S′1S′2…S′i－1S′i＋1…S′n；如果βMin≥90°，则以Si为圆心，以dave为半径在孔洞特征平面内作圆，再画S′i－1S′i和S′iS′i＋1的垂直平分线，交于圆四点P1，P2，P3，P4，如图4所示。由图可以发现P2，P4位于孔洞多边形外部，因此填充点主要根据P1，P3来确定；当｜P1P3｜＜dave，在P1P3中点位置添加填充点P，更新多边形为S′1S′2…S′i－1PS′i＋1…S′n；当dave≤｜P1P3｜＜d2ave时，在P1和P3位置分别添加填充点，更新多边形为S′1S′2…S′i－1P1P3S′i＋1…S′n；当｜P1P3｜≥d2ave时，则在P1和P3位置添加填充点，并更新多边形为S′1S′2…S′i－1P1S′iP3S′i＋1…S′n。在更新多边形后，重新计算βMin，并按上述方法进行循环处理。

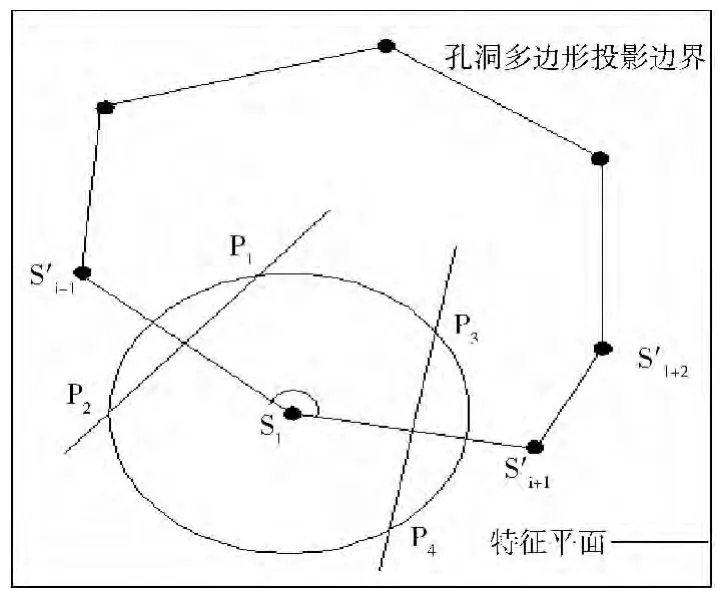
图4 βMin≥90°时孔洞填充

步骤4 根据新增填充边界边在孔洞边界特征平面上的投影与特征多边形是否相交检查新增填充点的合法性，删除非法的填充点。

3 基于径向基函数的孔洞修复

3.1 基于径向基函数的隐式曲面

等值线追踪法实现简单，但是需大量后期人工作业进行修订，因此，该方法效率低、劳动强度大，且易受主观因素影响。

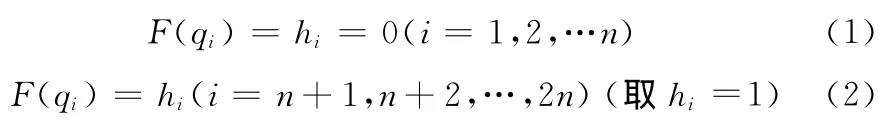
步骤2 以任意孔洞点为起点，查找其k邻域，删除与Q中元素重复的点，剩余点加入到点集Q；

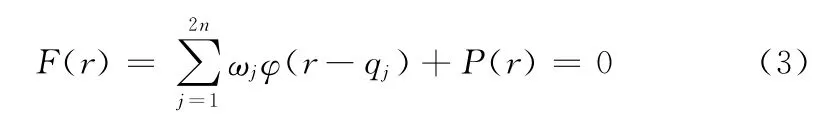
式中:r——建立曲面时通过的任意散乱点，qj——建立曲面所需的采样点，ωj对应每个采样点的权值，P（r）通常表示为P（r）＝p0＋p1x＋p2y＋p3z，φ（r－qj）为径向基函数，一般情况下，在对空间散乱点进行插值时经常用的基函数形式对于三维空间中的任意两个散乱点，为求解权值和一阶多项式的系数值，除由两类约束点所给定的约束值条件，还需要满足正交条件

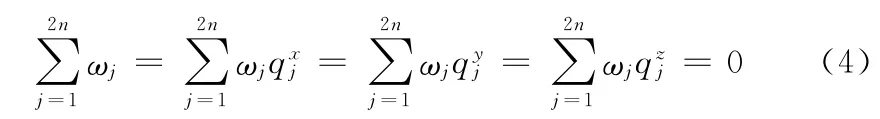
由此建立线性方程组AX＝B。由于系数矩阵A是插值约束点和附加约束点的插值条件决定的半正定矩阵，方程有唯一解，X是要求的权值ωj和一阶多项式的系数（p0，p1，p2，p3），B是约束值为hj的列向量，通过高斯消元法可以求出方程的解。

3.2 插值约束点

步骤1 读入提取得到的孔洞边界点，将其加入到插值约束点集Q中；

阿里巴巴集团CEO张勇表示，饿了么将依托阿里集团数字经济生态的商业基础设施，与阿里众多业务产生奇妙的化学反应，成为阿里新零售战略的一支重要力量。并购之后的饿了么将保持独立品牌、独立运营，饿了么的所有合作伙伴及商家的权利都将得到一如既往地尊重。同时，饿了么将进一步得到阿里巴巴在新零售基础设施、产品、技术、组织等方面的全力支持。

要建立点云孔洞的隐式曲面，就需要采集足够的数据点，如果没有考虑孔洞周围的点，新增填充点就难以与整个点云模型实现平滑过渡。为了完整地描述该隐式曲面，本文采集孔洞边界点及其k（本文取k＝6）邻域点作为插值约束点，主要过程如下:

构建基于径向基函数的隐式曲面表示为

步骤3 重复步骤2，直到遍历完所有的孔洞点，得到所需的插值约束点集。

3.3 附加约束点

仅仅只有插值约束点还不足以描述整个曲面，还应采集定义曲面所需要的附加约束点。采用法矢约束得到的附加约束点能够体现曲面的几何特性［11］，根据插值约束点的法矢计算出附加约束点。

为促进幼果快速膨大、减少畸形果与落果、提早上市，可以喷施赤霉酸5～6 mg/L+芸苔素0.02～0.03 mg/L。

为了检验匹配后各变量在处理组与控制组的分布是否变得平衡，本文进行了匹配平衡性检验，结果如表4所示。经过半径为0.01的半径匹配，所有变量的标准误绝对值下降幅度明显。在匹配完成后，t检验伴随概率值过高，接受处理组与控制组的匹配变量不存在系统性差异的原假设。本文还进一步采用最近邻匹配法与核匹配法进行验证，匹配效果同样良好。

首先计算插值约束点的法矢，对于采集得到的每个插值约束点Qi（i＝0，1，…，n－1），查找其K邻域X＝｛（xi，yi，zi）｜i＝0，1，…，k－1｝，采用最小二乘法计算Qi与X作为参考依据的微切平面。

假设平面方程Ax＋By＋Cz＋D＝0，为了不失一般性，设C不等于0。该微切平面用矩阵表示为

式中

采用奇异值分解的方法求出该平面的法向量n→＝（A，B，C），用该向量近似描述插值约束点的法矢，在该法矢方向上（取0.3单位长度处）进行附加约束点采集，获得附加约束点。

3.4 计算隐式曲面方程

将采集到的n个插值约束点和n个附加约束点代入式（1）、式（2）中，联立式（4），采用高斯消元法解方程组，求解出插值约束点的权值和一阶多项式的系数，从而得到曲面的隐式方程

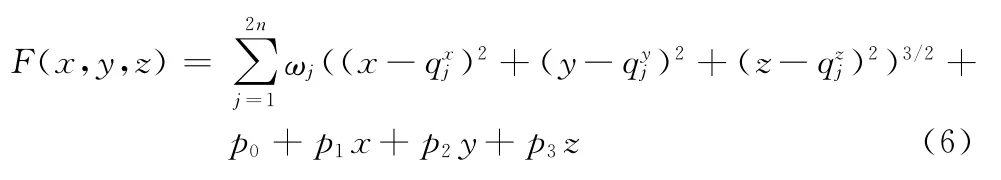
3.5 调整填充点至隐式曲面

梯度下降法是将需要迭代的点沿着负梯度方向以最快的速度逐步向曲面迭代逼近，梯度下降法的一般形式为［11］

通过两种焊条的工艺评定对比试验，选择出符合图纸技术要求的焊接材料，并制定相应的焊接工艺；该励磁机风扇已在电厂平稳运行两年多，表明焊材的选择及焊接工艺的制定是正确的。

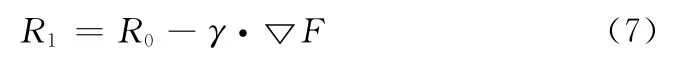
4 应用实例

本文实验以Windows操作系统为基础，以Visual C＋＋6.0为平台，结合OpenGL编程技术，完成实验平台的搭建，在该实验平台上进行点云孔洞修复处理。以带孔洞的散乱点云模型花瓶和兔子为例进行实验，其中花瓶模型孔洞曲率变化较小，兔子模型孔洞曲率变化较大，读取散乱点云并进行边界提取效果图如图6所示，采用本文算法进行孔洞修复的效果图如图7所示。

图5 新增点向曲面调整

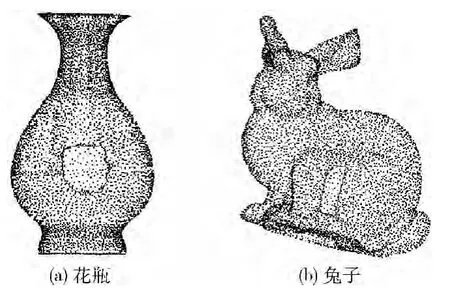
图6 散乱点云孔洞模型边界提取效果

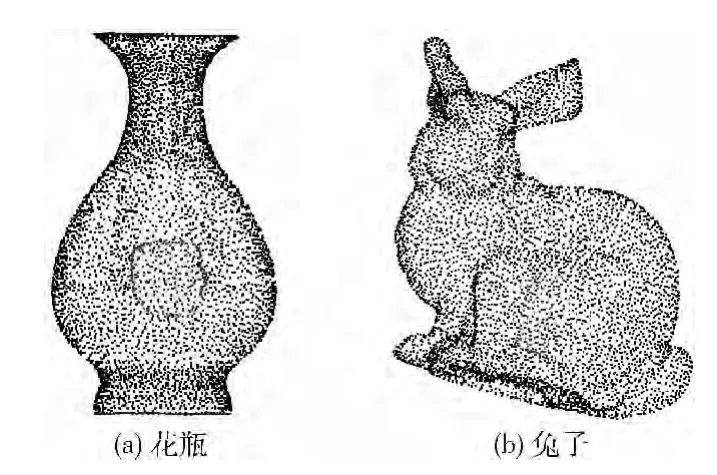
图7 孔洞修复效果

花瓶和兔子模型的散乱点、孔洞边界点和新增填充点个数见表1。

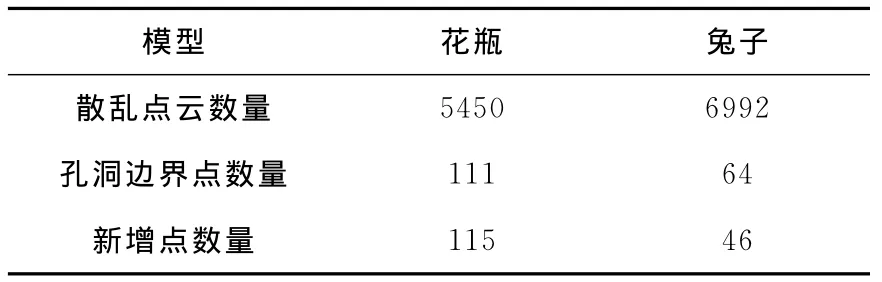
表1 模型相关点个数

为了更直观地观察孔洞修复效果，将填充后的散乱点云模型进行三角化处理后，如图8所示，从图8中可以看出，新增的孔洞点与先前孔洞周围点云能够平滑过渡，保持了模型的基本几何特征。

图8 孔洞修复后的点云模型三角化效果

5 结束语

提出了一种针对散乱点云模型的孔洞修补算法。采用二次划分的策略建立散乱点云空间拓补关系并进行K邻域搜索，根据采样点及其邻域点到基准平面的距离比值大小提取点云的孔洞边界，在孔洞特征平面上对孔洞进行二维填充，将填充点逐步向基于径向基函数的隐式曲面进行调整完成孔洞修复。在建立隐式曲面的过程中，充分利用了孔洞边界点及其邻域信息，能够实现孔洞修补点与原始点云之间的平滑过渡，修补效果良好。

［1］WANG Yinghui，WU Weiyong.Holes repairing algorithm of scattered data based on the fitting of partial subdivision curved surface［J］.Journal of Machine Design，2009，26（12）:72－74（in Chinese）.［王英惠，吴维勇.基于局部细分曲面拟合的散乱数据孔洞修补法［J］.机械设计，2009，26（12）:72－74.］

［2］TIAN Jianlei，LIU Xumin，GUAN Yong.Research on hole filling algorithm in triangle mesh models［J］.Journal of Computer Applications，2009，29（8）:2035－2037（in Chinese）.［田建磊，刘旭敏，关永.三角网络模型的补洞算法研究［J］.计算机应用，2009，29（8）:2035－2037.］

［3］GAO Fushun，GAO Zhanheng，LIANG Xuezhang，et al.Filling hole algorithm in triangle mesh［J］.Jourmal of Jilin University（Science Edition），2009，47（6）:1182－1184（in Chinese）.［高福顺，高占恒，梁学章，等.三角网格中的孔洞修补算法［J］.吉林大学学报（理学版），2009，47（6）:1182－1184.］

［4］Marchandise E，Piret C，Remacle J F.CAD and mesh repair with radial basis functions［J］.Journal of Computational Physics，2012:2376－2387.

［5］QIU Zeyang，SONG Xiaoyu，ZHANG Dinghua.Reparation of holes in discrete data points［J］.Journal of Engineering Graphics，2004（4）:85－89（in Chinese）.［邱泽阳，宋晓宇，张定华.离散数据中的孔洞修补［J］.工程图学学报，2004（4）:85－89.］

［6］CHEN Feizhou，CHEN Zhiyang，DING Zhang，et al.Filling holes in point cloud with radial basis function［J］.Journal of Computer－Aided Design ＆Computer Graphics，2006，18（9）:1414－1419（in Chinese）.［陈飞舟，陈志杨，丁展，等.基于径向基函数的残缺点云数据修复［J］.计算机辅助设计与图形学学报，2006，18（9）:1414－1419.］

［7］LIU Yuehua，LIAO Wenhe，LIU Hao.Research of K－nearest neighbors search algorithm in reverse engineering［J］.Machinery Design ＆Manufacture，2012（3）:256－258（in Chinese）.［刘越华，廖文和，刘浩.逆向工程中散乱点云的K邻域搜索算法研究［J］.机械设计与制造，2012（3）:256－258.］

［8］SUN Dianzhu，ZHU Changzhi，LI Yanrui.An improved extraction of boundary characteristic from scattered data［J］.Journal of Shangdong University（Engineering Science），2009，39（1）:84－86（in Chinese）.［孙殿柱，朱昌志，李延瑞.散乱点云边界特征快速提取算法［J］.山东大学学报（工学版），2009，39（1）:84－86.］

［9］GU Yuanyuan.Research and implement of hole－repairing technology for scattered points cloud［D］.Suzhou:Soochow University，2008:19－32（in Chinese）.［顾园园.散乱点云孔洞修补技术的研究与实现［D］.苏州:苏州大学，2008:19－32.］

［10］DU Ji，ZHANG Liyan，WANG Hongtao，et al.Hole repairing in triangular meshes based on radial basis function［J］.Journal of Computer－Aided Design ＆Computer Graphics，2005，17（9）:1976－1982（in Chinese）.［杜佶，张丽艳，王宏涛，等.基于径向基函数的三角网格曲面孔洞修补算法［J］.计算机辅助设计与图形学学报，2005，17（9）:1976－1982.］

［11］Tasso Karkanis，James Stewart.Curvature dependent triangulation of implicit surface［J］.IEEE Computer Graphics and Application，2001，21（2）:60－69.