Vakhnenko-Parkes方程的李对称及其精确解

温双全, 李春海, 莫达隆

(1. 桂林电子科技大学 数学与计算科学学院, 广西 桂林 541004; 2. 贺州学院 理学院, 广西 贺州 542800)

1 引言与预备知识

非线性演化方程已应用于数学物理学,如：生物学、流体力学、化学、凝聚物理学、光纤通信和量子场论.由于非线性演化方程应用于许多数学物理模型中,所以这些方程的精确解变得越来越重要并且促进了数值解的验证和解的稳定性分析,而许多解的存在性可能只依赖于一个单一变量.过去几年,有许多方法已用于寻求这类方程的精确解,如反散射法[1]、Backlund变换[2]、Hirota法[3]、对称法[4]、李群方法[5]、动力系统分支理论[6]、同伦摄动法[7].

Vakhnenko方程是一个在松弛介质下描述高频波的非线性演化方程[8-9],Vakhnenk方程简称VE,即

(1)

其中,u是无限维压强,x是空间变量,t是时间变量.由于VE有类似圈孤解的形式,则获得其方程的解比较困难.目前,学者们研究该方程已有些成就,如文献[10-11]运用同伦分析法发现该方程存在一个圈孤解形式;而V. Vakhnenko等[3]运用Hirota法[3]和反散射法[1,12]发现了2个圈孤解形式;而A. Morrison等[13]运用Hirota法[13]和反散射法[12]分别获得了N个圈孤解形式和计算多个圈孤解形式.

目前许多作者进一步研究

(2)

其中

若p=q=1,方程(2)是广义VE[13-14].若p=2q,方程(2)是修正的广义VE[15].广义VE和修正的广义VE都存在圈孤解、峰孤解和尖孤解.本文主要运用李群方法和动力系统理论来研究从VE演化而来的Vakhnenko-Parkes[16-17](VP)方程

uuxxt-uxuxt+u2ut=0.

(3)

2 Vakhnenko-Parkes方程的李对称

李群方法又称作李对称分析方法[5,18].相对较严谨地说法,微分方程的李对称群是将方程的一个解映射为方程的另一个解.微分方程的不变性将导出它的对称群所满足的充分必要条件,这组条件即称为对称群的决定方程组.确定了对称群的决定方程组,随之即可得到许多相应的应用.

设单参数李变换群的无穷小变换为

x→x+εξ(x,t,u),

t→t+ετ(x,t,u),

u→u+εφ(x,t,u),

其中无穷小参数ε≪1.设

(4)

为单参数李变换群的向量场,其第1,2,3阶延拓向量场如下

方程(3)在无穷小变换下保持不变当且仅当向量场应满足李对称条件pr(3)V(Δ)|Δ=0,其中

Δ=uuxxt-uxuxt+u2ut.

应用李对称条件到方程(3),可知系数函数ξ(x,t,u)、τ(x,t,u)、φ(x,t,u)必须满足如下对称条件

uxxtφ+2uutφ-uxtφx+

u2φt-uxφxt+uφxxt=0,

(5)

其中,φx、φt、φxt、φxxt是延拓向量pr(3)V的系数,并且有

φx=Dxφ-uxDxξ-utDxτ,

(6)

φt=Dtφ-uxDtξ-utDtτ,

(7)

φxt=DtDx(φ-ξux-τut)+ξuxxt+τuxtt,

(8)

ξuxxxt+τuxxtt,

(9)

其中,Dx和Dt分别是对x和t的全微分.置换(6)～(9)式到(5)式,并用uxuxt替换uuxxt+u2ut,得到VP方程的决定方程组

ξu=ξt=0,ξ=ξ(x),

(10)

τx=τu=0,τ=τ(t),

(11)

φuu=φx=φt=0,φ=φ(u),

(12)

-2φu+2ξx+τt=0, 3φu-τt=0.

(13)

解上面这些方程组,有如下系数函数

ξ=c1x+c2,τ=-6c1t+c3,

φ=-2c1u.

(14)

其中,c1、c2、c3是任意常数.可见方程的不变群的全体生成元构成了一个3维李代数,并且有下列一组基

(15)

与它们相应的单参数变换群

G1:(x,t,u)→(x+ε,t,u),

G2:(x,t,u)→(x,t+ε,u),

G3:(x,t,u)→(xeε,te-6ε,ue-2ε).

由此可见G1是空间变换,G2是时间变换,G3是尺度变换.因此,由表1可知V1、V2、V3的交换算子是封闭的.

3 Vakhnenko-Parkes方程的广义对称

应用广义对称方法考虑VP方程的对称.广义对称方法又简称待定系数法.

设VP方程的对称

σ(x,t,u)=a(x,t)ut+b(x,t)ux+

c(x,t)u+d(x,t),

(16)

其中,a(x,t)、b(x,t)、c(x,t)、d(x,t)是未确定的系数函数.根据广义对称方法,对称应满足下列条件

uxxtσ+2uutσ+u2σt-uxtσx-

uxσxt+uσxxt=0.

(17)

把(16)式及其相应的微分项代入(17)式,得到下列系数函数的表达形式

a(x,t)=-6c1t+c3,

b(x,t)=c1x+c2,

c(x,t)=2c1,d(x,t)=0.

(18)

于是得到VP方程的对称

σ=c3ut+c2ux+

c1(xux-6tut+2u),

(19)

其中,c1、c2、c3是任意常数.因此,得到VP方程的对称如下形式

σ1=ux,σ2=ut,

σ3=xux-6tut+2u,

(20)

这与第二节给出的对称是一样的.

4 Vakhnenko-Parkes方程的对称李代数的一维最优系统

下面给出VP方程的李代数的最优系统[19-21].为了获得该方程的最优系统,计算了李代数的交换子和李代数的伴随表示分别见表1和表2.

定理1方程的对称代数的一维最优系统有

V1,V2,V3,V1±V2.

(21)

表 1 换位子

表 2 李代数的的伴随表示Ad(exp(ε Vi))Vj

证明设VP方程对称代数的一维子代数的一般向量

V=a1V1+a2V2+a3V3,

其中,a1、a2、a3是不全为零的任意常数.下面对一维李代数进行分类,为了进一步简化一般向量,考虑下面几种情况:

1)a3≠0.用Adexp(ε1V1)作用V上有

V=(a1-ε1a3)V1+a2V2+a3V3.

取ε1=a1/a3,则V1项被消掉,V被约化为

V=a2V2+a3V3.

又取ε2=-a2/6a3,用Adexp(ε2V2)作用于V上,消掉V2项,则该情形下V等价于V=V3.

2)a3=0.V等价于V=a1V1+a2V2.

(a) 若a1=0,a2≠0,则该情形下V等价于V=V2;

(b) 若a1≠0,a2=0,则该情形下V等价于V=V1;

(c) 若a1≠0,a2≠0,用Adexp(ε3V3)作用于V上,可选取适当的ε3,使得V1和V2的系数相等或相反,则该情形下V等价于V=V1±V2.

总而言之,VP方程对称代数的一维子代数的最优系统Θ为{V1,V2,V3,V1±V2}.

5 Vaknenko-Parkes方程的精确行波解

当前考虑VP方程的行波解,设ξ=κx+ωt,有u(x,t)=φ(κx+ωt),其中κ和ω是增长波速.把它代入方程(3),得到如下非线性常微分方程

κ2wφφ‴-κ2wφ′φ″+wφ2φ′=0.

(22)

方程(22)对ξ进行积分有

3κ2φφ″-3κ2(φ′)2+φ3=g,

(23)

其中g是积分常数.方程(23)等价于平面

(24)

系统(24)有首次积分

(25)

其中h是积分常数.

显而易见在奇异线φ=0,系统(24)是无穷维的,这样的系统称为奇异行波系统.为了避免出现奇异情形,作变换dξ=φdτ.系统(24)转化成正则系统

(26)

系统(24)与系统(26)有相同的首次积分即不变曲线解,并且除了在奇异线φ=0外,系统(26)与系统(24)有相同的拓扑结构.

令M(φe,ye)为系统(26)在奇点(φe,ye)的系数矩阵,J(φe,ye)为系统(29)在奇点(φe,ye)的雅可比行列式,则有

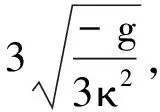
i=1,2,P2-4q>0.

由平面动力系统分支理论[6],有如下结论：

1)g>0,N是一个中心点;

2)g=0,O(0,0)是一个高阶奇点;

3)g<0,N是一个鞍点,P1和P2是2个结点.从而得出(24)和(26)的相图分支如图1所示.

根据系统(26)的相图进行分析讨论,得出VP方程的几种行波解如下.

图1 系统(24)和(26)的相图Fig. 1 Phase portraits of system (24) and (26)

(27)

置(27)式于系统(24)的第一个方程积分有

其中

(φ3-φ)(φ-φ2)(φ-φ1)=

则有如下参数表达式

φ(ξ)=φ3-(φ3-φ2)sn2(ω1ξ,k1),

(28)

其中

sn(u,k)是雅可比椭圆函数.因此,存在VP方程的周期行波解

φ(x,t)=φ3-

(φ3-φ2)sn2(ω1(κx+ωt),k1).

(29)

5.2孤波解

1) 当g=0时,存在一条同宿轨道穿过平衡点O(0,0)位于势函数h>0,则系统(25)变成

(30)

置(30)式于系统(24)的第一个方程积分,有参数表达式

(31)

2) 当g<0时,存在3条异宿轨道穿过奇点N,P1和P2位于势函数h>0,则系统(25)变成

(32)

置(32)式于系统(24)的第一个方程积分,有参数表达式

其中

因此,VP方程的孤立波解的参数表达式为

(33)

本文对VP方程运用经典李群方法进行了李对称分析,获得该方程的对称群的李代数结构,并且运用广义对称方法对其进行分析,发现此种方法下,该方程的李代数与前者是一样的.在伴随表示作用下,进一步研究了该方程的一维最优系统,并给出了证明.此外,运用动力系统方法研究了该方程的分支相图,根据相图探讨了该方程的一些精确解,并且找出其精确解的参数表达式.

[1] Vakhnenko V, Parkes E, Michtchenko A. The Vakhnenko equation from the view point of the inverse scattering method for the KdV equation[J]. Int J Diff Eqns Appl,2006,1(4):429-449.

[2] Vakhnenko V, Parkes E, Morrison A. A Backlund transformation and the inverse scattering transform method for the generalised Vakhnenko equation[J]. Chaos,Solitons and Fractals,2003,17(4):683-692.

[3] Vakhnenko V, Parkes E. The two loop soliton solution of the Vakhnenko equation[J]. Nonlinearity,1998,11(6):1457-1464.

[4] Bluman G, Kumei S. Symmetries and Differential Equations[M]. New York:Springer-Verlag,1989.

[5] Liu H, Li J. Lie symmetry analysis and exact solutions for the short pulse equation[J]. Nonlinear Anal,2009,71(5/6):2126-2133.

[6] Chen A, Ma Z. Bifurcation method of dynamical systems for generalized Kadomtsov-Petviashvili- Benjamin-Bona-Mahony equation[J]. Pramana J Phys,2008,71(1):57-63.

[7] He J. The homotopy perturbation method for nonlinear oscillators with discontinuities[J]. Appl Math Comput,2004,151(1):287-292.

[8] Vakhnenko V. Solitons in a nonliear model medium[J]. J Phys,1992,A25(15):4181-4187.

[9] Vakhnenko V. High-frequency soliton-like waves in a relaxing medium[J]. J Math Phys,1999,40(4):2011-2020.

[10] Nahhas A. Analytic approximations for the one-loop soliton solution of the Vakhnenko eqaution[J]. Chaos,Solitons and Fractals,2009,40(5):2257-2264.

[11] Wu Y, Wang C, Liao J. Solving the one-loop soliton solution of the Vakhnenko equation by means of the Homotopy analysis method[J]. Chaos,Solitons and Fractals,2005,23(5):1733-1740.

[12] Vakhnenko V, Parkes E. The calculation of multi-soliton solutions of the Vakhnenko equation by the inverse scattering method[J]. Chaos,Solitons and Fractals,2002,13(9):1819-1826.

[13] Morrison A, Parkes E, Vakhnenko V. TheN-loop soliton solutions of the Vakhnenko equation[J]. Nonlinearity,1999,12(5):1427-1437.

[14] Morrison A, Parkes E. TheN-soliton solution of a generalised Vakhnenko equation[J]. Glasgow Math J Trust,2001,43:65-90.

[15] Morrison A, Parkes E. TheN-soliton solution of the modified generalised Vakhnenko equation(a new nonlinear evolution equation)[J]. Chaos,Solitons and Fractals,2003,16(1):13-26.

[16] Abazari R. Application of (G′/G)-expansion method to traveling wave solutions of three nonlinear evolution equation[J]. Computers and Fluids,2010,39(10):1957-1963.

[17] Jafari H, Kadkhode N, Khalique C. Traveling wave solutions of nonlinear evolution using the simplest equation method[J]. Comput Math Appl,2012,64(6):2084-2088.

[18] Liu H, Li J, Liu L. Lie symmetry analysis, optimal systems and exact solutions to the fifth-order KdV types of equation[J]. J Math Anal Appl,2010,368(2):551-558.

[19] 刘若辰,何文丽,张顺利,等. 非线性发展方程的一维最优系统[J]. 西北大学学报:自然科学版,2003,33(4):383-388.

[20] 张颖,屈长征. Zero-coupon bond pricing模型的最优系统和对称约化[D]. 兰州:西北大学,2009.

[21] Chou K, Qu C. Optimal systems and group classification of (1+2)-dimensional heat equation[J]. Acta Appl Math,2004,83(3):257-287.

[22] 马知恩,周义仓. 常微分方程定性理论与稳定性方法[M]. 北京:科学出版社,2001.

[23] Liu H, Li J. Lie symmetry analysis and exact solutions for the extended mKdV equation[J]. Acta Appl Math,2010,109(3):1107-1119.