人民币均衡汇率研究

(上海财经大学 国际工商管理学院/世界经济与贸易系，上海 200433)

一、引言及文献综述

购买力平价(Purchasing Power Parity，简称PPP)是指任意两国之间一篮子特定商品的价格如果被换算成同一种流通货币，应该是等值的。换句话说，均衡时的汇率(间接标价法)应该是两个国家货币的购买力的比率，这类似于金本位制时，国家之间的汇率由它们各自货币的含金量之比——金平价来决定。购买力平价理论最早由瑞典经济学家Cassel在1918年提出。[3]

然而，购买力平价理论有着很强的甚至不现实的假设条件，它要求两个国家的所有商品都是可以贸易的，而且是无摩擦的贸易。这就意味着，购买力平价的基本原理依赖于完美套汇。而在现实中，大量的非贸易商品、各种各样的贸易和非贸易壁垒、运输成本等等广泛存在，这些都在很大程度上使得套汇交易是不完美的。因此，实际汇率的实证数据都很大地违背了购买力平价，尤其是短期数据。然而，直觉上的吸引力仍然让很多经济学家相信购买力平价的一些变体形式可以很好地用在长期的实际汇率上(Dornbusch and Krugman，1976；[8]Rogoff，1996[19])。

但是购买力平价在长期是否成立仍然处于争论之中。早期的研究，像Roll(1979)[20]和Adler，Lehmann(1983)[2]都显示实际汇率符合随机游走(Random Walk)模型。在20世纪80年代后期，Engle Granger’s(1987)[12]以及许多后来的研究都显示出实际汇率是一个差分平稳过程。但是，正如Frankel(1986和1990)[13][14]指出的那样，无法拒绝单位根假设可能是由于对实际汇率变化观测值有限导致。如果扩大样本量，单位根的基本假设也许就被拒绝了。例如，Frankel(1986)[13]用美元和英镑在1864年到1984年的实际汇率来计算，就拒绝了单位根假设，Abuaf和Jorion(1990)[1]用多个国家实际汇率的面板数据也得出了拒绝假设的结论。不幸的是，长时间序列方法和面板数据方法都似乎是有问题的。长时间序列数据没有考虑到在这么长的样本时间内出现汇率政策变动的可能，而面板数据的方法可能存在过分拒绝单位根假设的问题，哪怕面板数据只有一个实际汇率没有单位根，那么整个面板数据就会拒绝单位根假设。

但是购买力平价的拥护者使用传统的线性方法始终不能回答以下两个现象，或“两个谜题”(Taylor，Peel和Sarno，2001)[23]。第一个难题是为什么实际汇率相对于它们的名义值如此的不稳定，不能收敛于按PPP理论得出的某种均衡值。第二个难题是既然购买力平价在长期应该成立，为什么实际汇率均值回归的速度这么慢？

从20世纪80年代末期开始，各种非线性动态购买力平价研究方法迅速发展，它们都是为了解决上述两个难题的。(Taylor and Taylor，2004)[24]这类模型考虑到了商品市场和资本市场存在摩擦的问题。大家知道，各种交易成本(关税、运输成本、运输时间等等)和沉没成本使得套汇交易不完全。因此，即便存在一个由购买力平价得出的均衡实际汇率，在现实中也一定存在一种围绕着均衡汇率的“无套利区间”。只要在这个区间里即使汇率偏离了均衡水平，套汇也不发生。这种模型被叫做门限自回归(threshold autoregressive，简称TAR)。那么第一个难题现在可以被解释为，实际汇率符合随机游走因为它处于“无套利区间”。门限自回归模型现在已经被广泛应用于实证研究中，而且已经被证实能够很好的与数据匹配。(例如，Prakash and Taylor，1996；[18]Obstfeld and Taylor，1997；[17]Sarno，Taylor，and Chowdhury，2004[21])在此基础上，Granger and Tersvirta (1993)[15]基于异质性交易人的假设，把门限自回归模型扩展成了“平滑传递自回归”模型(smooth-transition autoregressive，简称STAR)。[25]直观上，货币交易者所占有的信息集和其做决定的方法上是有异质性的，因此交易者在“无套利区间”上有不同的观点。然而，如果离均衡汇率的偏差太大，大多数代理人还是会朝同一个方向进行交易，此时偏差将会快速地缩小。因此，不存在突然的或者离散的偏差调整，它是相当连续的。而且当偏差小的时候调整速度更慢，当偏差大的时候调整速度更快。同时汇率浮动中“懒惰的S形”调整过程也是支持这种观点的(Taylor and Taylor, 2004)[24]。因此，多数学者认为STAR模型是解决这两个难题的好方法。

到目前为止，针对中国汇率的研究还很不充分，也缺乏有说服力的均衡汇率。这主要与中国政府对汇率和资本市场的严格管控有关。严格的管控使得套汇交易非常不完美，而且产生了一大片“无套利区间”。结果导致在中国均衡的实际汇率在不同的研究中变化非常大(例如，Chou and Shih, 1998;[4]陈学彬, 1999;[27]任兆璋和宁忠忠, 2003[28])。然而，中国最近大量地购买美国债券的事实揭露了中国的汇率已经很大程度地偏离了均衡状态，以至于超过了无套利区间的边界，因此中国被迫人为地操纵汇率。而这么做的代价就是中国这个世界上最大的发展中国家虽然自己急需要别人的投资，自己却成为了美国公共部门的最大投资者[29]。

随着这种代价的快速上升和中国向世界开放资本市场的承诺，把汇率调整到一个安全的范围内越来越紧急，这可以避免大范围套汇行为的发生。由于STAR模型在解释汇率浮动上的巨大成功，笔者决定使用STAR模型里的一个变体来研究中国的汇率并尝试找出合理的汇率和安全的浮动范围，这样由人民币低估可能引发的经济危机就可以被很好的规避了。

二、均衡汇率模型和平滑门限自回归模型

1、均衡汇率的确定

确定均衡汇率有两种主要的理论。购买力平价理论主要基于套利。另一个理论主要基于内外部平衡。这种理论的例子包括基本的均衡利率机制(Williamson，1983)[26]、自然的实际汇率法(Stein，1994)[22]、行为均衡汇率法(Clark and MacDonald, 1999)[5]和均衡汇率理论(Edwards，1989)[11]。

一方面，尽管购买力平价理论直截了当，但它忽视了大量非贸易品的存在，所以购买力平价有着固有的缺陷，正如Balassa-Samuelson效应所展示的那样。另一方面，基于一般均衡的一些理论在理论上是合理的，但是机制上却比购买力平价复杂得多，增加了实证应用的难度。因此笔者认为，一个研究均衡汇率的理想模型应该能很好地将购买力平价和一般均衡方法融合在一起，也就是一个有着一般均衡微观基础的购买力平价模型。笔者借用Cuong Le Van, Ceeile Couharde, and Thai Bao Luong’s (2006)[6]的一般均衡模型，但做出了一定的拓展。

考虑一个小型的开放经济体，有两个生产部门，贸易品部门“T”和非贸易品部门“N”。劳动在国内可以自由移动，但在国际间不能移动，用字母l表示。由于劳动力在国内可以自由移动，所以工资在一国之内都是相等的，用字母w表示。资本在国内和国家间都可以自由移动，用字母k表示。利率用字母r表示。贸易品部门和非贸易品部门的劳动生产率分别用AT和AN表示。国际商品市场无摩擦，套汇完美，购买力平价成立。

生产方程是Cobb-Douglus方程：

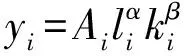
生产者利益最大化的问题是：

maxli,ki{Pi-wli-rkk}；

消费者利益最大化的问题是：maxCTCN{lnCT+ζlnCN}，她的约束条件是PTCT+PNCN+PTM=PTYT+PNyn+PTX，这里CT和CN分别是对贸易品和非贸易品的消费量。

M代表进口，X代表出口。再者，内部平衡要求CT+X=yT+M，同时CN=yN;而外部均衡要求PT(M-X)=λ(PTyT+PNyN)，这里λ代表着外国负债与GDP的比率。

因此，均衡价格水平可以被表示成：

lnP=lnγ-lmβ+(1-α-β)[θlnθ(1-θ)ln(1-θ)]-θlnAT-(1-θ)lnAN

(1)

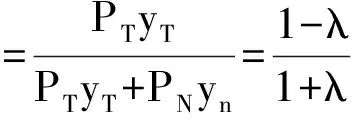
(2)

如果(1-α-β)[θlnθ+(1-θ)lnθ]这项是恒定的话，那么方程(2)可以被重写成：

(3)

这里A=θlnAT+(1-θ)lnAN，代表着全要素生产率(Total factor productivity，简称TFP)。方程(3)就是笔者用的均衡汇率模型。它代表了均衡汇率由利率变动差别的微分和TEP两者决定。

2、有交易成本下的汇率：平滑门限自回归模型

因为STAR模型既有合理的理论基础又能很好地被实证数据验证，多数学者认为它是目前为止最好的模型。该模型认为，各种各样的贸易成本和投资中的沉没成本决定了汇率偏差的门槛(例如，Dixit, 1989;[7]Krugman, 1989;[16]Dumas,1992[9])。在门槛内，有一个无套利区间，导致套汇行为不发生。因此，在这个区间内的偏差应该是一个随机游走过程，正如短期数据所显示的那样。如果汇率偏差在门槛外，那么套汇会使得它朝着均衡状态回复。因此购买力平价在长期应该成立。更进一步，交易人异质性假设使得交易机制的转变是连续的而不是离散的(Dumas，1994)[10]。此外，这个假设也表明了当汇率离均衡状态越远的时候，返回的速度越快。这个不恒定的返回速度可以用汇率浮动中的“懒惰的S”过程来表示(Taylor and Taylor，2004)[24]。

基于STAR模型在解释非线性动态汇率变动上的优势，笔者选择STAR模型中的一个变体来研究中国的汇率。笔者的主要任务是找到均衡汇率和安全的浮动范围。

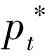
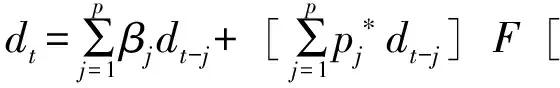
(4)

这里{dt}是一个平稳遍历过程，εt～iid(0,σ2)；θ∈R+，表示均值回复速度的系数；F[θ，dt-d]是决定均值回复程度的函数；p∈N是滞后的顺序，d(1，2，…，p)是延期的顺序。

蒸了几个小时，仍不见百里香归来。川矢按捺不住，命人揭开蒸笼，一股怪味直扑口鼻。川矢心中狐疑，抽出军刀切出一段，对刁德恒说：“你的米西米西！”刁德恒吃过前几次亏，这回就乖多了。他毕恭毕敬地接在手中，硬着头皮吃了下去。

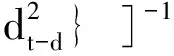
其实这两个方程比较起来的话，没有哪一个比另一个有绝对的优势。但是，既然大多数研究用的是ESTAR模型(例如，Taylor, Peel, and Sarno, 2001;[23])，笔者就选用ESTAR模型来给汇率动态建模。

三、数据和估计

笔者用方程(3)来估计内外部均衡下的购买力平价得出的均衡汇率，用方程(4)来估计考虑到贸易成本和沉没成本存在的非线性动态汇率偏差。

(1)均衡汇率的估计

方程(3)中，笔者用全要素生产率(TFP)和利率的数据来估计均衡汇率。因为人民币是以美元作为兑换管理的，并且与其他货币的汇率都是以交叉汇率为基础，因此笔者只用关注人民币对美元的汇率，即一单位美元兑换人民币的价格。1979年到2006年的数据，比如GDP、劳动力、投资、GDP平减指数和CPI等均来源于中国统计年鉴和美国经济分析中心(Bureau of Economic Analysis)。资本则由基于真实投资的永续盘存制构建。而真实投资是通过用GDP平减指数来平减国内总资本形成的方法获得。此外，笔者使用1979年之前的一系列投资数据来构建基准年的资本存量。并且假设第一个十年投资的平均增长率能够很好地当作早于基准年投资状况的代理变量。

而中美两国的全要素生产率(TFP)由索洛剩余(solow residuals)估计。

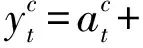
(5)

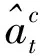
(6)

这里字母上的帽子代表拟合值的意思。而且TFP改变率的拟合值(基于年度数据)可以被下式得出：

(7)

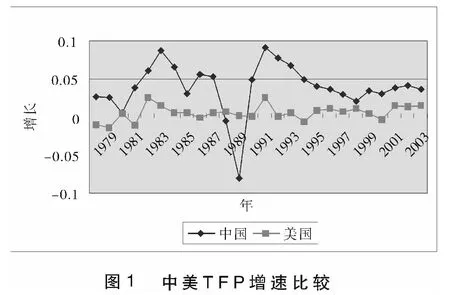
关于中美两国1979-2006年全要素生产率(TFP)增长的比较可以在“图1”中体现。中国的TFP增长率比美国高出很多，这主要归因于中国从计划经济到市场经济的转变带来了生产效率的提高和国际贸易利得。尽管起伏没有那么大，但是美国在1983、1990和2003年TFP增长率的波动也是与它的历史经济周期相一致的。

笔者分别用中美的借贷利率作为中美利率的代理变量：中国的贷款利率数据从《金融年鉴(1979-2001)》和中国人民银行(2002 -2006)获取；美国的贷款利率从国际金融统计(IPS)数据库(1979-2006)获得。通过方程(3)，笔者可以计算出均衡汇率的动态变化。为了获得均衡汇率的水平值，笔者需要找到一个合理的均衡汇率作为基础。考虑到中美两国在1990年都经历过一次经济危机并且在1994年两国经济都被认为完全恢复。基于此，笔者认为两国经济在1994年都达到了国内外收支平衡的状态，所以把1994年汇率的购买力平价值作为基础参照。这里引用Chou and Shih (1998)[4]的估计，认为1994年中美两国的均衡汇率为7.85。

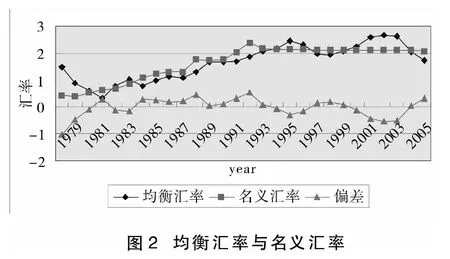
图2反映的是中国的均衡汇率的对数值，实际的每年平均汇率以及1979到2006年间的变化。有趣的是，图2显示出1992年之前的均衡汇率与实际情况非常接近。笔者将这种现象解释为1992年中国有限的商业贸易和外商直接投资活动使得汇率具有稳定性，这也使得中国政府很容易根据宏观的经济数据对汇率做出调整。然而，1992年之后，激增的对外贸易活动和外商直接投资使得均衡汇率极具变动性。因此，一个在中国人民银行干预之下非常稳定的汇率不能再反映外汇的实际变动情况。相对稳定的名义汇率和潜在的波动的均衡汇率也引发了关于人民币价值是否被低估或高估的激烈争论。笔者看来，这场争论很大程度上源自于不同的研究者所关注的时间点的不同。例如，如果笔者讨论2004年人民币的汇率，那么人民币应该贬值，因为它远低于均衡水平。而2005年，情况正好相反。

(2)无套利区间的估计

在将STAR模型应用于评估中国汇率的非线性结构之前，笔者有两个步骤要做。第一步是检查时间序列的平稳性。运用STAR模型的一个先决条件是研究的过程应该是平稳的。考虑到时间序列是平稳的，下一步应该是确定时间序列里lag(s)的数量和p值，和延期变量d∈{1，…，p}。

第一步，对平稳性的非增强迪基-富勒检验(Dickey-Fuller Test)。

为了检验汇率序列的平稳性，笔者应用了增强的迪基-富勒检验(Dickey-Fuller Test)。正如在表1中展示的那样，DF统计值为-2.57，p值为0.11。这意味着笔者只能在11%的显著性水平下拒绝过程有单位根的零假设。类似的问题在其他相对短期的汇率数据中也存在。但是，无法拒绝单位根假设并不一定意味着笔者应该接受它。正如Taylor, et al. (2001)[23]认为的那样，即使汇率本身是平稳的，汇率的非线性结构仍可能导致单位根问题。Taylor and Taylor(2004)[24]也用Monte-Carlo实验来证明拒绝单位根假设的失败可能是由数据的时间跨度短导致的。然而，当笔者检查汇率的一阶差分时，表1展示了非增强的DF统计值为-2.25，p值为0.026。这意味着笔者至少可以在5%的显著性水平下拒绝原假设。同时汇率一阶差分值的平稳性也已经在美元兑法郎、美元兑英镑和美元兑日元的汇率数据中被证实。

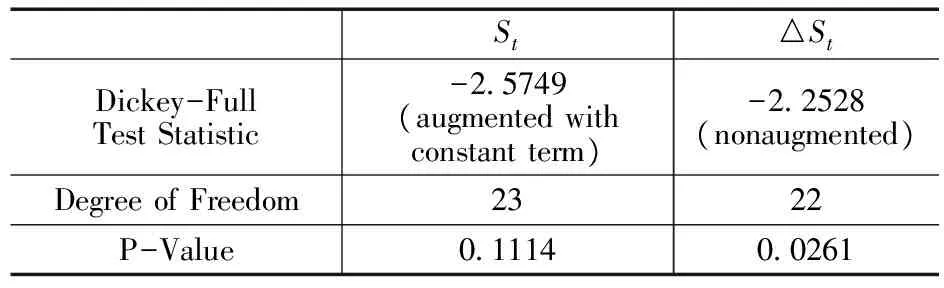
表1 单变量线性单位根检验

注:St表示名义汇率的对数; △St表示一阶差分。

第二步，滞后函数Lags(p)和延期函数Delays(d)的选择

在实证上很难想象影响一国汇率的因素可能会滞后至多三年。所以笔者只比较lag(s)在0-3之间的AIC值。表2展示不同lag(s)数值对应的AIC值，因此滞后一期，p=1的情况被选中，因为这种情况在对数据保持最强解释力的同时能够维持解释变量最小化。

表2 不同AP(P) (P=0,1,2,3)下的AIC值

注： 粗体的AIC是不同滞后期下的最小值，说明了AR(1) ，即滞后一期是该实证模型的最优选择。

既然选择了p-1，那么对d∈{1，…，p}的选择就应该是d=p=1。

正如在前面展示的那样，笔者选1，…，择ESTAR模型来估计中国1979～2006年汇率的非线性动态情况。在这里，当d=p=1的时候，ESTAR模型可以被表示成：

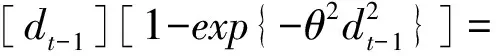
(8)

类似于Tayloretal.(2001)[23]的观点，笔者出于简洁性的目的，分别将和设定为正一和负一。正如在表3中展示的那样，均值回归系数θ=1.3739，在1%的显著性水平下显著不等于1。

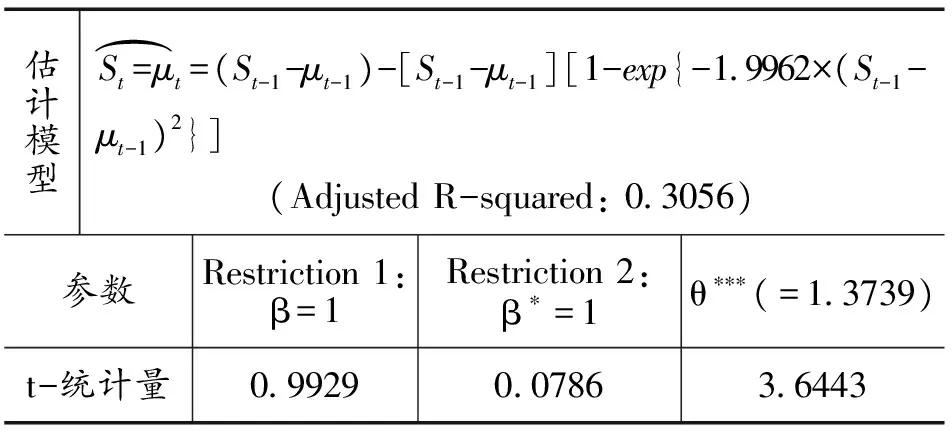
表3 非线性回归结果

注: 字母上的小帽子代表估计值.

而拟合值方程(9)可以被表示为：

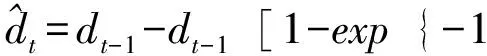
(9)

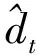
一个50%冲击的响应函数可以在图3中被表示出来，它显示了冲击的半衰期稍稍多于两年的时间，这和用其他汇率算出的2-3年的半衰期是接近的。响应函数还清楚地展示了当接近均衡水平时，均值回归速度呈下降趋势。也就是说，当接近均衡时(大概在5%的偏差内)，汇率几乎可以被看作是随机游走过程。而且，图2也展示出当偏差超过10%的时候，套汇行为大量出现。因此对于中国的货币当局来说，一条首要法则就是时刻警觉10%这条线。

四、结论

STAR模型具有很多优良性质，它不仅具有良好的理论基础，还与实际汇率的实证动态数据相吻合。贸易中的交易成本和投资中的沉没成本阻止了完美的汇率套利的形成，产生了无套利区间。在这种无套利区间中，套利行为不会发生而且购买力平价提出的均值回归过程也通常无法进行。因此，在这种状态下的汇率几乎是一个随机游走过程。然而，当汇率离均衡状态的偏差很大的时候，套汇仍然发生，使得汇率朝着均衡水平移动。这时候购买力平价成立。在现实中，异质性的交易人对套汇的门槛的看法不一样。但更多的交易人在当汇率很大程度远离均衡时才开始套汇，也就是说这时候的均值回归速度也会特别快。因此均值回归过程应该是平滑的而不是分割的，而且速度递减随着汇率更接近均衡值。

笔者运用STAR模型的变体——ESTAR模型来研究中国1979年到2006年间汇率波动情况。首先，笔者使用了一个考虑到内外部平衡的一般均衡模型来估计均衡汇率。然后，通过调查中国汇率的动态行为，笔者识别出ESTAR模型应该有一年的滞后和一年的延期。根据模型的特定形式，笔者使用非线性的最小二乘估计法估计出参数。再根据估计的参数，得出一个50%的冲击(偏离均衡水平50%)的半衰期稍微多于两年。并且笔者也可以算出大致在10%以上的偏离就会面临严重的套汇压力。因此对于中国人民银行来说应该将10%的汇率偏差作为他们的警戒线。

(编辑：余华；校对：周亮)

[1]Abuaf, Niso and Philippe Jorion. Purchasing Power Parity in the Long Run[J]. Journal of Finance, 1990，(1)：157-174.

[2]Adler, Michael and Bruce Lehmann. Deviations from Purchasing Power Parity in the Long Run[J]. Journal of Finance, 1983，(5)：1471-1487.

[3]Cassel, Gustav. Abnormal Deviations in International Exchanges[J]. Economic Journal, 1918，(28)：413-415.

[4]Chou, W. L. and Y. C. Shih.. The Equilibrium Exchange Rate of Chinese Renminbi[J]. Journal of Comparative Economics, 1998，(26)：165-174.

[5]Clark, P.B. and R. MacDonald.. Exchange Rates and Economic Fundamentals: A Methodological Comparison of BEERs and FEERs[M]. R. MacDonald and J. Stein, Equilibrium Exchange Rates. Amsterdam: Kluwer，1999.99-104.

[6]Cuong Le Van, Ceeile Couharde, and Thai Bao Luong.. The De-termination of the Equilibrium Exchange Rate in a Simple General Equilibrium Model[J]. Review of Development Economics, 2006，(3)：506-517.

[7]Dixit, A. K.. Hysteresis, Import Penetration and Exchange Rate Pass-Through[J]. Quarterly Journal of Economics, 1989，(104)： 205-228.

[8]Dornbusch, Rudiger and Paul Krugman. Flexible Exchange Rates in the Short Run[J]. Brookings Papers on Economic Activity, 1976，(3)： 537-575.

[9]Dumas, B. Dynamic Equilibrium and the Real Exchange Rate in Spatially Separated World[J]. Review of Financial Studies, 1992，(5)：153-180.

[10]Dumas, B. Partial Equilibrium Versus General Equilibrium Models of the International Capital Market[A]. F. Van Der Ploeg, The Handbook of International Macroeconomics (Oxford: Blackwell)[C]. 1994.10.

[11]Edwards, S. Real Exchange Rate in the Developing Countries: Concept and Measurement[N]. NBER Working Paper, No.2950:(1989).

[12]Engle, Robert and CliveW. J. Granger. Co-integration and Error Correction: Representation, Estimation and Testing[J]. Econometrica, 1987，(2)：251-276.

[13]Frankel, Jeffrey A.International Capital Mobility and Crowding-out in the U.S. Economy: Imperfect Integration of Financial Markets or of Goods Markets in How Open is the U.S. Economy R. W. Hafered[M]. Lexington, Mass.: Lexington Books, 1986.33-67.

[14]Frankel, Jeffrey A.Zen and the Art of Modern Macroeconomics: A Commentary[M]. in Monetary Policy for a Volatile Global Economy. William S. Haraf and Thomas D. Willett. Washington, D.C.: AEI Press, 1990：117-123.

[15]Granger, Clive W. J. and Timo Tersvirta. Modelling Nonlinear Economic Relationships[M]. Oxford: Oxford University Press，1993.

[16]Krugman, P. R.. Exchange Rate Instability[M]. Cambridge, MA: MIT Press，1989：102-107.

[17]Obstfeld, Maurice and Alan M. Taylor.. .Nonlinear Aspects of Goods-Market Arbitrage and Adjustment: Heckscher’s Commodity Points Revisited[J].Journal of the Japanese and International Economies, 1997，(4)： 441-479.

[18]Prakash, Gauri and Alan M. Taylor. Measuring Market Integration: A Model of Arbitrage with an Econometric Application to the Gold Standard, 1880-1913[M]. Working Paper Series no. 6073, National Bureau of Economic Research (June)，1997.31-34.

[19]Rogoff, Kenneth.The Purchasing Power Parity Puzzle[J].Journal of Economic Literature, 1996，(2)：647-668.

[20]Roll, Richard.Violations of Purchasing Power Parity and their Implications for Efficient International Commodity Markets, in International Finance and Trade[M]. Vol. 1. M. Sarnat and G.P. Szego. Cambridge MA: Ballinger，1979.34-37.

[21]Sarno, Lucio, Ibrahim Chowdhury and Mark P. Taylor. NonLinear Dynamics in the Law of One Price: A Broad-Based Empirical Study[J].Journal of International Money and Finance, 2004，(23)：1-25.

[22]Stein, J.. The Natural Real Exchange Rate of the US Dollar and Determinants of Capital Flows. in. J. Williamson Estimating Equilibrium Exchange Rate[M]. Institute for International Economics; Washington，1994.99-104.

[23]Taylor, Mark P., David A. Peel and Lucio Sarno. Nonlinear Mean-Reversion in Real Exchange Rates: Towards a Solution to the Purchasing Power Parity Puzzles[J].International Economic Review, 2001，(42)：1015-1042.

[24]Taylor, Alan M. and Mark P. Taylor.The Purchasing Power Parity Debate[J].Journal of Economic Perspectives, 2004，(8)：135-158.

[25]Tersvirta, T. Specification, Estimation and Evaluation of Smooth Transition Autoregressive Models[J]. Journal of the American Statistical Association, 1994，(89)： 208-218.

[26]Williamson, J.The Exchange Rate System[M]. Institute for International Economics, Washington，1983.67-69.

[27]陈学彬.近期人民币实际汇率变动态势分析——兼谈分析实际汇率应注意的问题[J〗.经济研究，1999，(1)：22-28.

[28]任兆璋，宁忠忠.购买力平价理论与人民币汇率升值压力实证分析[J].南方金融,2003，(12)：19-23.

[29]牛 拥，毛德勇.人民币升值对中国制造业出口竞争力的影响[J].贵州财经大学学报，2013，(6)：22-27.