基于遗传算法的OFDM高精度盲频偏估计器
杨朝阳,杨霄鹏,李 腾,姚 昆,倪 娟
(1. 空军工程大学 信息与导航学院,西安 710077;2. 解放军94303部队,山东 潍坊 261100)
1 引 言
正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)系统凭借其固有的抗多径效应、频谱利用率、低实现复杂度迅速成为研究热点并被应用于多个无线标准,如IEEE 802.11a/g、802.16、数字视频广播、LTE、B3G等[1]。然而,OFDM子载波之间需要保持正交,导致其对载波频偏非常敏感。由于收发端晶振频率失配或多普勒效应造成的载波频偏会破坏子载波间的正交性,产生载波间干扰(Inter Carrier Interference,ICI),极大地恶化了系统性能。
针对这一问题,国内外学者已经提出了多种频偏估计的算法。这些算法可以归结为两大类:数据辅助类[2-4]和非数据辅助类(盲估计)频偏估计算法[5-10]。数据辅助类估计算法利用收发端已知的训练序列估计载波频偏,该类算法性能较好,计算量小,但需要消耗额外的功率和带宽资源。盲频偏估计算法由于不需要训练序列或符号重传,具有高频带利用率,成为近年来的研究热点。文献[4]提出了基于循环前缀的最大似然频偏估计算法,其性能跟循环前缀的长度有关,且受多径影响较大。文献[5]提出了两种适用于BPSK调制的载波频偏盲估计算法,但只适用于BPSK调制,受调制类型的限制。文献[6]提出了基于虚子载波的多信号分类(Multiple Signal Classification,MUSIC)频偏估计算法,通过最小化虚子载波上的信号功率来估计频偏,但是该算法需要已知虚子载波的位置,不利于信道的动态分配。文献[7]利用黄金分割算法减小了虚子载波算法的计算量。文献[8]提出了基于最小输出方差(Minimum Output Variance,MOV)盲频偏估计算法,该算法不需要虚子载波且较MUSIC算法估计精度高,但是需要较多的数据块。文献[9]提出了适用于恒包络调制的盲频偏估计算法,但是其受调制类型的限制。针对以上盲频偏估计存在的问题,文献[10]提出了一种新的基于最小重建误差(Minimum Reconstruction Error,MRE)的盲频偏估计算法,在一定频偏范围内代价函数为单峰函数,利用黄金分割搜索算法寻找代价函数最小值估计频偏,然而该算法频偏估计范围较小。
本文在文献[10]基础上,提出了一种基于遗传算法(Genetic Algorithm,GA)的高精度盲频偏估计器。在频偏估计范围较大时代价函数是多峰函数,此时黄金分割搜索算法容易陷入局部最优,不一定能够找到全局最优解。本文利用GA强大的随机搜索能力求得最佳频偏估值,并且跟MOV、黄金分割算法做了对比分析。仿真结果表明,基于GA的盲频偏估计算法较MOV算法、黄金分割搜索算法估计精度高,低信噪比下性能显著,且不受频偏估计范围和调制类型的限制。
2 系统模型
带载波间干扰的接收信号在第K个载波上的接收信号可以表示为
Y(k)=X(k)H(k)S(0)+
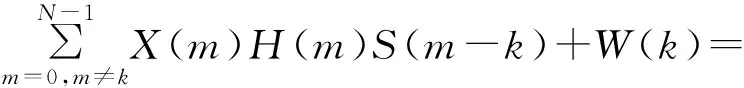
X(k)ΛS+W(k)
(1)
式中,N表示子载波的个数,X(k)、Y(k)分别表示第k个子载波上的发送、接收符号,H(k)表示第k个子载波上的信道衰落增益,Λ=diag(H(0),H(1),…,H(N-1))表示衰落对角矩阵,当信道为高斯信道时H(k)=1,W(k)表示加性高斯白噪声,S(m-k)表示载波间干扰系数:
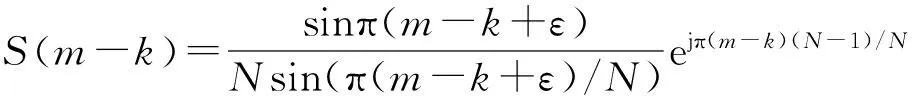
(2)
式中,ε表示归一化载波频偏,ε=ΔF/Δf,ΔF是频偏,Δf是子载波的间隔,S是N×N的ICI系数矩阵,S矩阵的第p行q列的元素为Sp,q=S(p-q)。完整的S矩阵为

(3)
观察式(1)可以发现,带ICI干扰的接收信号可以被视为N个用户的多载波码分多址接入(Multi Carrier Code Division Multi Access,MC-CDMA)系统,第K个用户的信息符号为X(k),第K个用户的扩频码对应矩阵S的第K列[10]。通过对ICI的系数矩阵做特征值分解可以得到
S=FHΦ(ε)F
(4)
式中,Φ表示对角矩阵,Φ=diag(φ0,φ1,…,φN-1),其中φn=exp(j2πεn/N);矩阵F是归一化的离散傅里叶变换矩阵(DFT),FH是矩阵F的共轭转置矩阵。通过公式(5)的推导得到ICI的系数矩阵S为一个正交矩阵。
SSH=(FHΨ(ε)F)(FHΨ(ε)F)H=
(FHΨ(ε)F)(FHΨ(-ε)F)=I
(5)
因此,可以把存在ICI的OFDM接收信号视为正交MC-CDMA系统,其对应的扩频码为S。对接收信号Y乘以如下式所示的矩阵可以得到
R=YSHΛ-1=X+WSHΛ-1
(6)
由于SH为正交矩阵,所以WSH和W的互协方差矩阵是相等的。因此,可以根据R的符号对X作出判决,从而达到完全消除ICI的效果。然而在接收端归一化载波频偏ε未知,可以通过比较重建信号和接收端实际接收的信号来找出最佳的频偏估值。
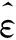
(7)
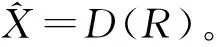
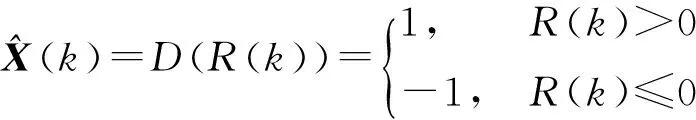
(8)

(9)
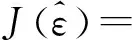

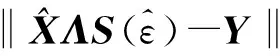


(10)

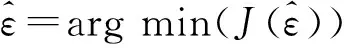
(11)
3 基于GA算法的盲频偏估计
黄金分割搜索算法是通过区间收缩求单峰函数极值的一种最优化算法,然而在代价函数为多峰函数时,黄金分割搜索算法容易陷入局部最优,不一定能找到全局最优频偏估值,也就是说黄金分割搜索算法频偏估计范围较小。为了找到最佳频偏估值,扩大频偏估计的范围,本文利用GA强大的并行随机搜索能力和全局寻优能力来求得最佳频偏估值。
图1为基于GA算法频偏估计流程图。遗传算法能够以很大概率收敛到最优频偏估值或近似最优频偏估值[11],因此,本文将频偏估计建模为最优化问题,并引入遗传算法进行求解。

图1 遗传算法频偏估计流程图Fig.1 The flow chart of frequency offset estimation based on genetic algorithm
频偏估计算法的参数设计及其步骤如下所述。
(1)编解码方式
假设归一化载波频偏在(-1,1)之间,采用二进制编码方式,码的长度取决于离散精度eps。
(12)
其中,l表示二进制编码的长度,假设一个频偏个体的编码为X:blbl-1bl-2…b2b1,则对应的解码公式为
(13)
(2)随机生成M个二进制数组作为频偏初始种群。
(3)适应度函数的设计
(14)

(4)选择算子采用按比例的适应度分配,也称之为轮盘赌或蒙特卡罗法。即频偏个体i的适应度为f(i),则其被选取的概率为
(15)
从上式可以看出适应度越高的频偏个体对应的选取概率也越大,遗传到下一代的概率也越大。
(5)交叉算子采用单点交叉方式,即在新复制的群体中随机取一个位置,以一定的概率两者互换从该位置起的末尾部分。模仿自然界基因重组,在对种群优化的同时保证了其多样性,决定了遗传算法的全局搜索能力。
(6)变异算子采用基本位变异算子,以一定的概率随机指定某一位二进制编码个体上的基因值作变异运算,即二进制编码取反。变异运算可以提升遗传算法对频偏的局部搜索能力,同时保持群体多样性,可以防止早熟出现。
4 仿真分析
仿真参数为:子载波数为64,循环前缀16,分别采用恒模调制QPSK、非恒模调制16 QAM调制,这是为了验证本文算法不受调制类型的限制,多径信道参数如表1所示。GA算法采用的参数为:归一化频偏估计的范围为(-1,1),种群数一般取值20~50之间,本文取为NP=25,最大进化代数为NG=50,交叉概率Pc=0.8,变异概率为Pm=0.04,精度eps=0.000 1,对应的二进制编码为15位。

表1 多径信道参数Table 1 The parameters of the multipath fading channel
如图2所示,图(a)、(b)分别为归一化频偏真实值为0.3、0.6,不同信噪比下代价函数跟频偏估值之间的关系曲线。可以看出在频偏估值分别为0.3、0.6时,即频偏估值跟真实频偏相等时,代价函数取得最小值,验证了理论分析。同时通过图2还可以得到,不论是恒模QPSK调制还是非恒模16QAM调制,代价函数在最佳频偏估值时均取得最小值,这使得该盲频偏估计算法不受调制类型的限制。
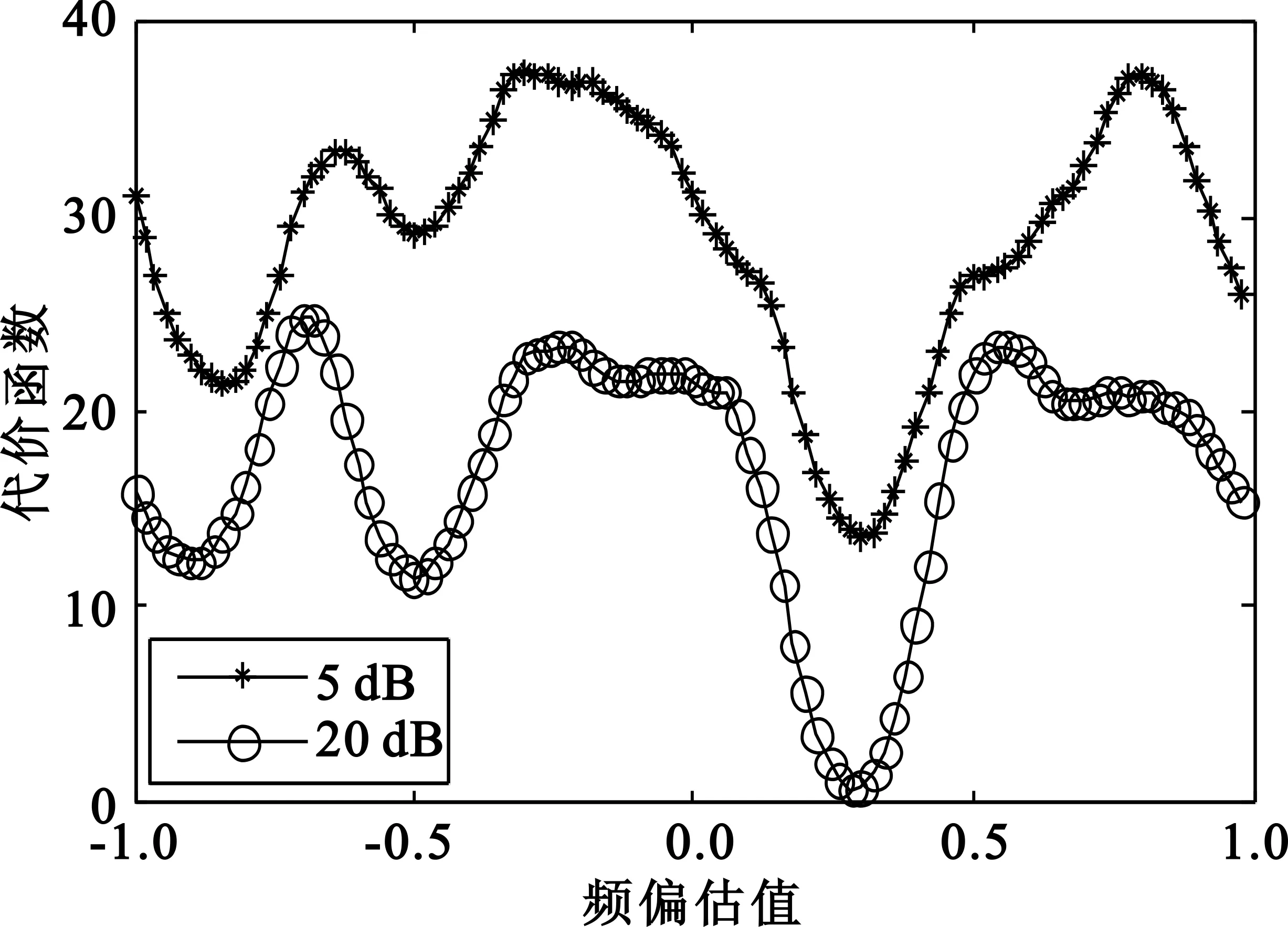
(a)QPSK调制下代价函数与频偏估值曲线

(b)16QAM调制下代价函数与频偏估值曲线
比较图3(a)、(b)可以得到,不论是在小频偏还是大频偏下基于遗传算法的盲频偏估计都能够在第5代左右收敛,同时还可以看出调制阶数对频偏估值没有影响。观察图3(c)可以得到本文提出的频偏估计算法具有很高的估计精度,且在很少代数时即可达到收敛,其计算量是可以接受的。
图4为信噪比15 dB、QPSK调制下,仿真1 000次求平均得到的每一代种群中代表频偏的最佳个体、最差个体和种群平均适应度曲线。通过图4可以看出种群中最优个体在第5代左右适应度曲线已经收敛,与此同时平均适应度和最小适应度也逐渐上升并达到收敛。

(a)QPSK调制ε=0.05时频偏估值曲线
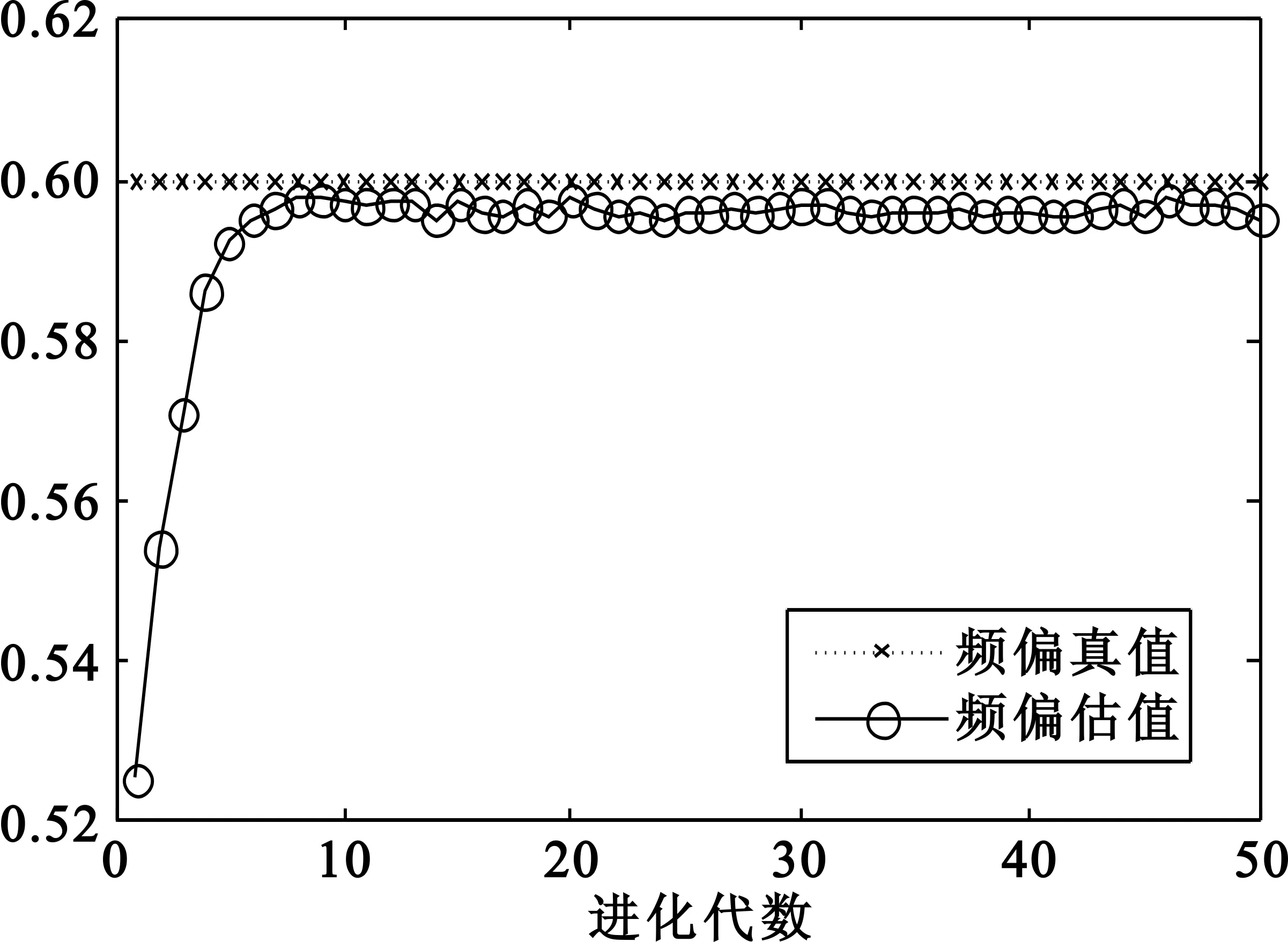
(b)16QAM调制ε=0.6时的频偏估值曲线

(c)频偏估计误差随进化代数曲线
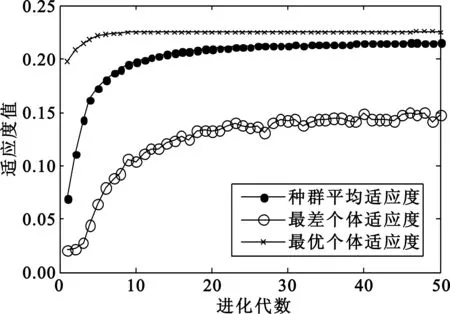
图4 适应度值随进化代数的变化曲线Fig.4 The fitness valuecurve versus evolution generation
定义频偏估计的均方误差(Mean Square Error,MSE)为
(16)
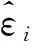
图5为频偏ε=0.3、P取1 000时的MSE对比曲线。MOV表示最小输出方差频偏估计算法,block前面的数字表示数据块的数目;MRE-Gold表示基于黄金分割搜索的最小重建误差频偏估计算法,其迭代次数取19,在(-0.5,0.5)区间收缩,则迭代19次后的区间变为(0.5+0.5)×0.61819=0.000 107,这跟遗传算法取的精度eps=0.000 1近似相等;MRE-GA表示本文提出的基于遗传算法的频偏估计算法,其搜索区间为(-1,1)。搜索区间可以根据需要进行设置,与此同时对应的二进制编码长度也会随之改变。通过观察图5可以看出基于最小重建误差的盲频偏估计算法具有很高的估计精度,在只有一个数据块时,在同一信噪比下其估计精度较MOV算法大约有一个数量级的提升。而本文所提出的基于遗传算法的盲频偏估计精度高于黄金分割搜索算法,尤其在低信噪比下较MRE-Gold算法具有更好的估计性能。结合图4可以看到遗传算法在迭代进行到第5代左右即可收敛,而黄金分割搜索算法需要迭代19次,其有效降低了时间复杂度,提高了实时性。同时本文所提算法不受频偏估计范围的限制,这是由遗传算法强大的全局寻优能力决定的。而黄金分割只适用于单峰函数求极值,其估计范围有限。因此,本文算法在实际应用中具备更大的适用范围和鲁棒性。

图5 多径信道下频偏估计MSE曲线Fig.5 The frequency offset estimation MSE in multipath fading channel
5 结束语
本文通过对基于最小重建误差的盲频偏估计算法的深入研究和分析,提出了基于GA算法的高精度盲频偏估计算法。所提算法将最优化思想与OFDM盲频偏估计相结合,利用GA算法强大的全局搜索和优化能力,提高了频偏估计的精度和频偏估计的范围。与此同时,该算法不依赖于任何特定的子载波分配方案,也不依赖于空子载波,所有载波都可以发送数据,具有较高的频谱效率。相对于枚举法、黄金搜索算法降低了时间复杂度,提高了系统实时性,这对实时要求较高的通信系统设计具有较大的参考价值。针对遗传算法早熟现象的改进算法在OFDM盲频偏估计中的应用有待进一步研究。
[1] 李丹,庄宏成.高速铁路3G及TD-LTE移动通信关键问题研究综述[J].计算机应用研究,2013,30(5):1297-1301.
LI Dan,ZHUANG Hong-cheng. Review of key technology of 3G and TD-LTE mobile communication systems for high-speed railway[J]. Application Research of Computers,2013,30(5):1297-1301.(in Chinese)
[2] Yu J H,Su Y T. Pilot-assisted maximum-likelihood frequency offset estimation for OFDM systems[J]. IEEE Transactions on Communications,2004,52(11):1997-2008.
[3] 张鑫明,叶锋,杨波,等.Sigma-Point卡尔曼滤波用于OFDM载波频偏估计[J].天津大学学报(自然科学与工程技术版),2013,46(5):458-462.
ZHANG Xing-ming,YE Feng,YANG Bo,et al. Application of Sigma-Point Kalman Filter to Carrier Frequency Offset Estimation of OFDM System[J]. Journal of Tianjin University(Science and Technology),2013,46(5):458-462.(in Chinese)
[4] Van de Beek J J,Sandell M,Borjesson P O. ML estimation of time and frequency offset in OFDM systems[J]. IEEE Transactions on Signal Processing,1977,45(7):1800-1805.
[5] 赵海龙,马上,张健,等.适用于OFDM-BPSK的载波频偏盲估计算法[J].电子科技大学学报,2012,41(6):842-846.
ZHAO Hai-long,MA Shang,ZHANG Jian,et al. Blind Estimation of Carrier Frequency Offset for OFDM-BPSK Systems[J]. Journal of University of Electronic Science and Technology of China,2012,41(6):842-846.(in Chinese)
[6] Tureli U,Liu H,Zoltowski M D. A high efficiency carrier estimator for OFDM communications[C]//Proceedings of the Thirty-First Asilomar Conference on Signals,System & Computers. Pacific Grove,CA,USA:IEEE,1998:505-509.
[7] 周德富,蔡惠智.一种高效的OFDM载波频偏盲估计方法[J].电讯技术,2012,52(1):33-37.
ZHOU De-fu,CAI Hui-zhi. A high-efficiency blind carrier frequency offset estimation approach for OFDM systems[J]. Telecommunication Engineering,2012,52(1):33-37.(in Chinese)
[8] Yang F,Li K H,Teh K C. A carrier frequency offset estimator with minimum output variance for OFDM system[J]. IEEE Communications Letters,2004,8(11):677-679.
[9] Oh J H,Kim J T. Blind carrier frequency offset estimation for OFDM systems with constant modulus constellations[J]. IEEE Communications Letters,2011,15(9):971-973.
[10] Li X,Han Q,Ellinger J,et al. General total inter-carrier interference cancellation for OFDM high speed aerial vehicle communication[C]//Proceedings of 2013 IEEE International Conference on Communications(ICC). Budapest,Hungary:IEEE,2013:4698-4702.
[11] 王小平,曹立明.遗传算法——理论、应用与软件实现[M].西安:西安交通大学出版社,2002.
WANG Xiao-ping,CAO Li-ming. Genetic Algorithm:theory,application and implementation with software[M]. Xi′an:Xi′an Jiaotong University Press,2002.(in Chinese)

