一种基于简化极化敏感阵列的APES波束形成算法
幸璐璐
(中国西南电子技术研究所,成都 610036)
1 引 言
极化域-空域联合的自适应波束形成技术可以克服纯空域滤波的不足,同时利用信号的极化信息和空域信息来完成滤波,因而具有比基于传统标量阵列的纯空域滤波更优的性能[1-2]。完备的电磁矢量传感器由空间同点放置、相互正交的3个电偶极子和磁偶极子构成,其结构紧凑,但阵元互耦效应明显,且制作成本高。现有的极化敏感阵列信号处理大多假设其阵元是由低维矢量天线构成,最常见的是两分量极化敏感阵列。文献[3]研究了一种由相互正交的电偶极子对构成的均匀线阵的滤波性能,阵列的每个阵元由两个电偶极子构成,两个电偶极子共点放置不可避免地具有明显的互耦效应。考虑将各阵元在空间分散放置,这虽然需要较大的载荷空间但是可以使阵元间的互耦效应相应降低。文献[4]中把极化敏感阵列划分成为了4种类型,其中阵列类型Ⅱ将阵元在空间分散配置,通过合理的稀疏布阵来减少阵元间互耦效应的影响。
近年来,基于极化敏感阵列的自适应波束形成技术受到越来越多的关注。文献[5]讨论了单个电磁矢量传感器的波束形成问题,文献[6]在文献[5]的基础上对其输出信干噪比的性能进行了分析。文献[7]基于四元数信号模型完成了极化域-空域联合的最小方差无失真响应(Minimum Variance Distortionless Response,MVDR)波束形成。文献[8]介绍了一种极化域-空域联合的自适应波束形成算法,将MVDR算法应用到极化敏感阵列滤波中,称为极化MVDR,但是该算法在强期望信号或是低采样快拍数的情况下其性能下降甚至失效,而且不具有对入射相干信号的解相干能力。幅度相位估计(APES)算法在多个领域都得到了重要而广泛的应用[9]。文献[10]将APES算法用于标量阵列的自适应波束形成,并将其与不同的波束形成算法对比分析了性能。文献[11]推导了基于前后向空间平滑的APES算法,它具有比文献[10]更优的滤波性能。为了克服极化MVDR算法[8]在特定环境下的性能下降或是失效,进一步提高极化敏感阵列的滤波性能,得到更为稳定的波束图,本文考虑将APES算法拓展到极化域-空域联合的自适应滤波中,提出一种简化极化敏感阵列的APES波束形成算法——极化APES算法,并通过仿真验证算法的性能。
2 信号模型
本文考虑由电偶极子对构成的极化敏感阵列,其阵列结构如图1(a)所示,此阵列类型又被称为两分量阵列。将两分量阵列各阵元分量在空间分散放置,可以得到简化的极化阵列示意图如图1(b)所示。各阵元沿y轴排列构成均匀线阵,阵元间距为d。

图1 阵列结构示意图Fig.1 Array pattern
假设空间有1个期望信号和J个干扰信号入射到极化敏感阵列,固定入射信号方位角φ=π/2,俯仰角为θ∈[-π/2,π/2]。阵列接收信号模型X(t)可以表示为
X(t)=[x1,x2,…,xM]T=
A·S(t)+N(t)
(1)
式中,sd(t)、si(t)分别表示期望信号和干扰信号的复包络;N(t)是零均值的复高斯白噪声;S(t)=diag([sd(t),s1(t),…,sJ(t)]T),A=[ad,a1,…,aJ],其中ad、ai分别为M×1维的期望信号和干扰信号的极化域-空域联合导向矢量。
对于空间共点放置的电偶极子对,其极化导向矢量aip可以表示为
(2)
其中,i=d,1,…,J;参数γ和η分别表示入射电磁波的极化相角和极化相位差;θ、φ分别表示入射信号的俯仰角和方位角。当固定入射信号方位角φ=π/2时,式(2)可以简化为
(3)
当相互正交的电偶极子对在空间分散放置时,各极子对入射信号具有不变的极化响应和不同的空间响应,这是由于入射电磁波到达各阵元的空间相位延迟所引起的。阵列的空间导向矢量表示如下:
ais=[1,e-jφi,…,e-j(M-1)φi]T
(4)
式中,j表示复数虚部单位,φi=2πdsinθi/λ,i=d,1,…,J。期望信号的极化域-空域联合导向矢量可以表示为
ad=[pdx,pdye-jφd,pdxe-j2φd,…,pdye-j(M-1)φd]T
(5)
上式中假设M为偶数。同理,干扰信号的导向矢量具有与公式(5)类似的形式。阵列接收信号的协方差矩阵
(6)
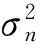
3 极化APES算法描述
将M阵元构成的均匀阵列按照图2所示划分为K个子阵,每个子阵包含有L个阵元,且满足L=M-K-1,即第k个子阵的首阵元与第k+1个子阵的首阵元具有相同的极化类型,且它们之间相差了一个不同极化类型的阵元。
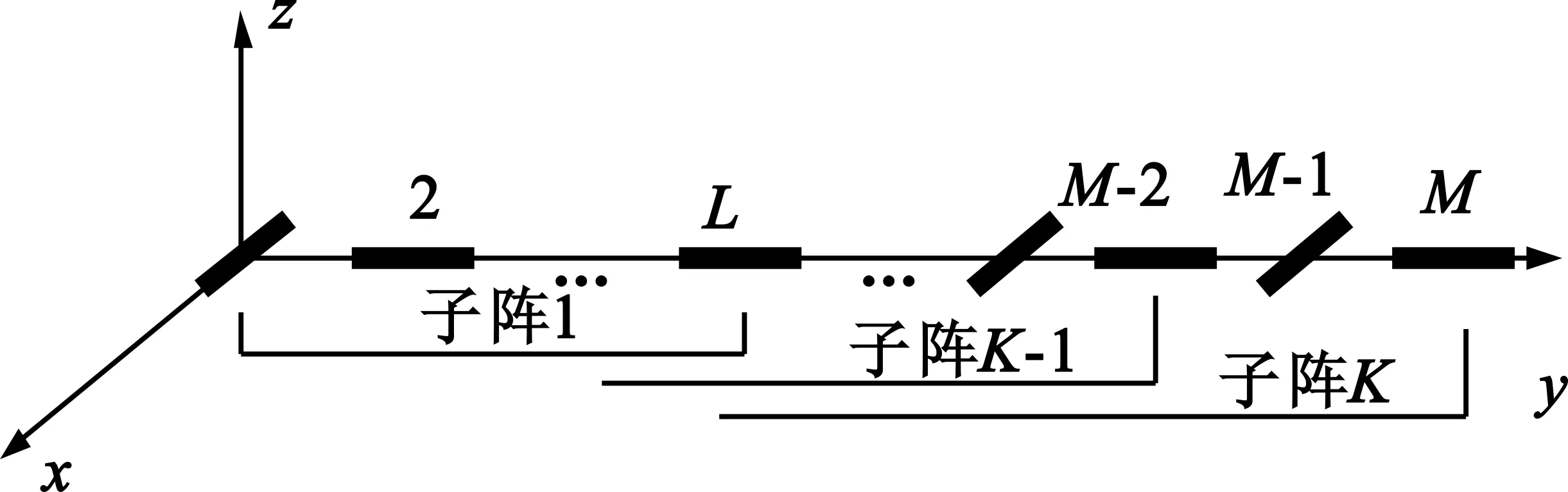
图2 子阵划分示意图Fig.2 Sub-array pattern
第k个子阵的接收信号为L×1维的列向量,满足
Xk(t)=[xk,xk+1,…,xk+L-1]T=Ak·S(t)+Nk(t)
(7)
其中,Ak为导向矢量A的第2k-1行至2k+L-2行,以A1为参考则有

(8)
定义矩阵ψ:
ψ=diag(e-j2φd,e-j2φ1,…,e-j2φJ)
(9)
则有Ak=A1·ψk-1,k=1,2,…,K。对每个子阵用相同的L×1维的加权向量w0进行极化域-空域联合滤波,将子阵k的接收信号重新表示为如下形式:

(10)
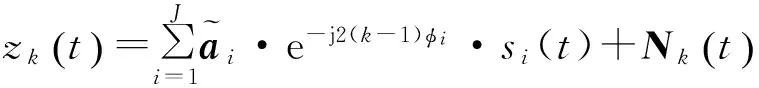
将Xk(t)通过加权向量w0后的输出信号为
(11)

(12)
(13)

(14)
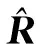
(15)
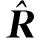
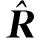
(16)
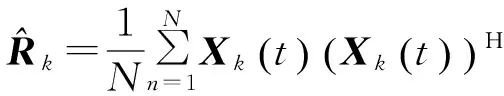
将f表示为如下矩阵的形式:
f=
(17)
其中,T为L×M维的Toeplitz矩阵,易得
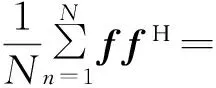
(18)
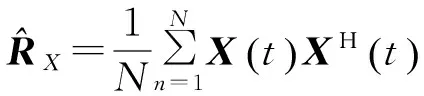
(19)
公式(19)完成了干扰加噪声信号协方差矩阵的估计。利用拉格朗日乘子法可以解得公式(14)的最优权向量w0,得
(20)
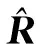
将各子阵的接收信号通过w0滤波后输出,再将各子阵输出信号yk(t)移相后相加求和,即可得到整个极化敏感阵列的输出
(21)
4 仿真分析
为了验证极化APES算法在强期望信号、低快拍数、入射信号相干的情况下仍可以获得较好的性能,将其与极化域-空域联合的极化MVDR算法对比。
仿真1:阵元数M=10,子阵个数K=3,每个子阵包含有L=6个阵元,阵元间距d=λ/2,采样快拍数N=512。期望信号入射角度(θd,φd)=(0°,90°),极化参数(γd,ηd)=(30°,60°),SNR=20 dB。一个干扰信号入射角度(θ1,φ1)=(-50°,90°),极化参数(γ1,η1)=(60°,90°),INR=20 dB。图3给出了两种算法在强期望信号的条件下输出方向图的对比。
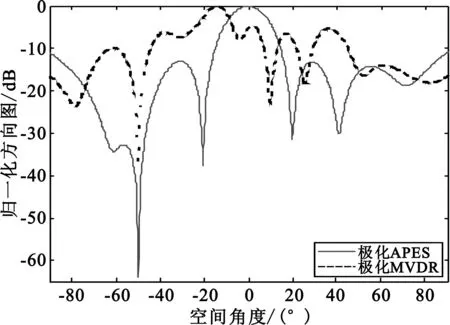
图3 强期望信号下输出方向图对比Fig.3 Directional pattern of strong expected signal
从图3可以看出,当入射期望信号功率较大时极化APES算法在干扰来波方向形成了很深的零陷,且主瓣对准了期望信号方向,而极化MVDR算法的主瓣不再对准期望信号来波方向,旁瓣电平抬高,此时算法失效。
仿真2:信号参数设置同仿真条件1,改变采样快拍数N=50,入射期望信号信噪比SNR=5 dB,图4给出了两种算法在低快拍数的条件下输出方向图的对比。
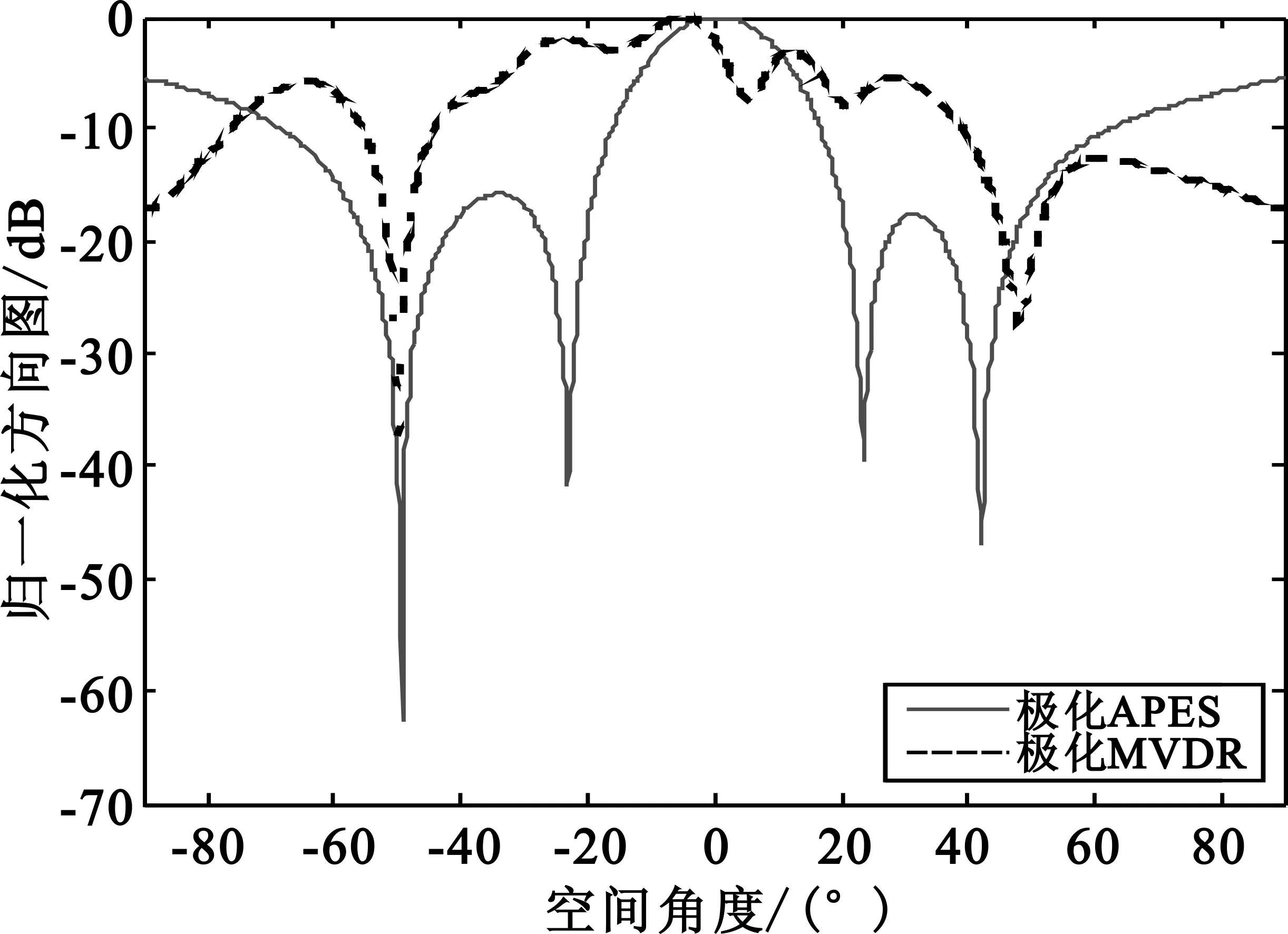
图4 低快拍数下输出方向图对比Fig.4 Directional pattern of low sampling number
从图4可以看出,在低快拍数的情况下,极化APES算法也具有较稳定的波束方向图,在干扰来波方向形成了较深的零陷,主瓣对准期望信号来波方向,而极化MVDR算法在快拍数较少时由于接收信号协方差矩阵的估计不准确导致其性能下降,波束图上并没有形成较好的主瓣。
仿真3:阵列基本参数设置同仿真条件1,期望信号入射角度(θd,φd)=(0°,90°),极化参数(γd,ηd)=(30°,60°),SNR=10 dB。假设空间有两个干扰信号入射,一个与期望信号相干的干扰信号入射角度(θ1,φ1)=(-50°,90°),另一个与期望信号不相干的干扰信号入射角度(θ2,φ2)=(60°,90°),极化参量各不相同,干噪比均为INR=20 dB。图5给出了两种算法在存在相干信号的情况下输出方向图的对比。
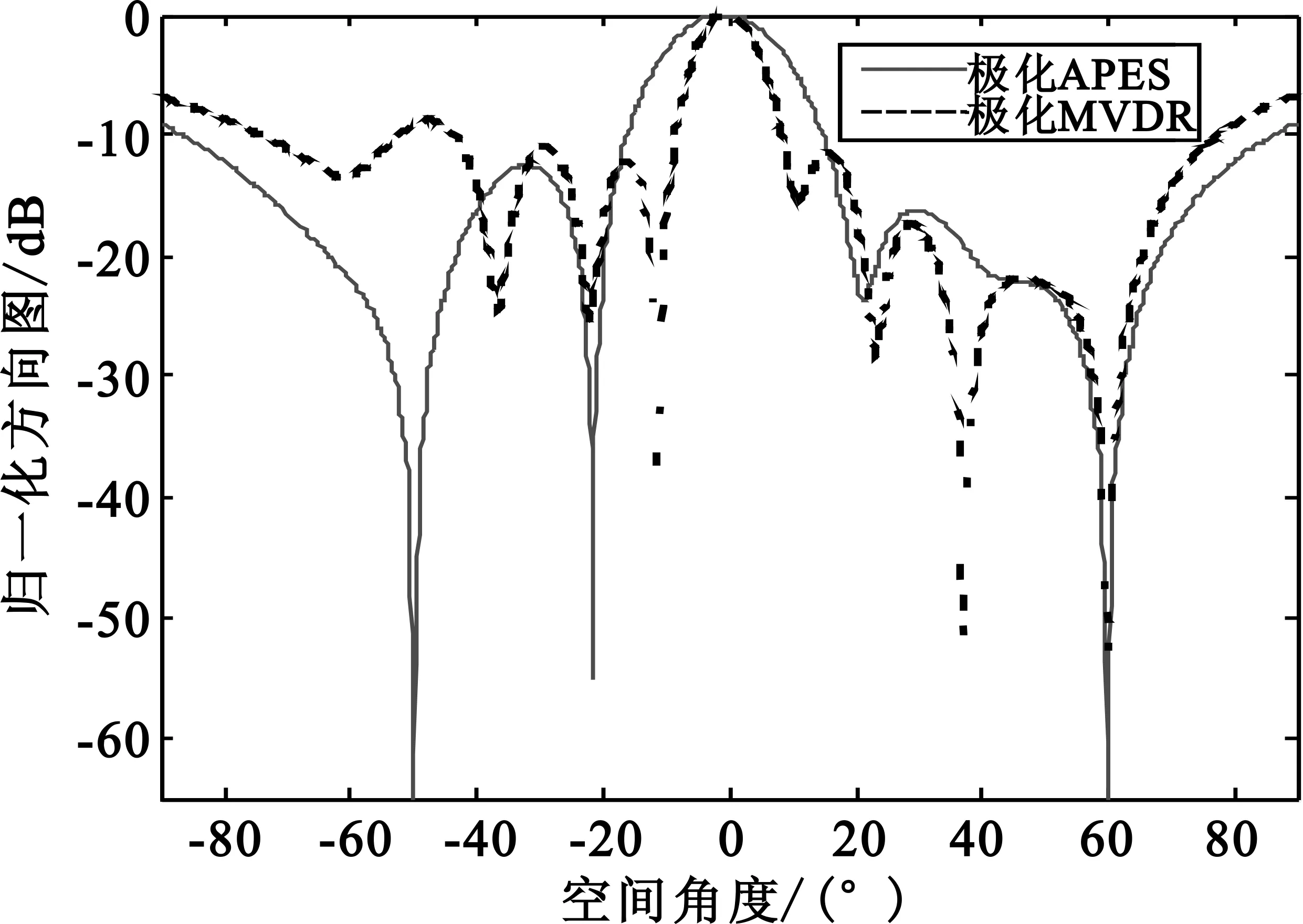
图5 空间一个相干信号对波束图的影响Fig.5 Beam pattern with one coherent signals
从图5可以看出,极化APES算法在相干干扰的情况下在两个干扰信号来波方向都形成了较深的零陷,主瓣对准期望信号方向,形成了较稳定的波束图,说明极化APES算法具有对相干信号的解相干能力。极化MVDR算法在相干干扰信号来波方向形成了谱峰,即把干扰信号当成了期望信号,不具有对相干信号解相干的性能,此时算法失效。
5 结束语
本文将常规的空域APES波束形成算法扩展到极化域-空域联合的自适应波束形成中,同时为了减少常规极化敏感阵列共点阵元之间互耦的影响提出了基于简化极化敏感阵列的APES波束形成算法。计算机仿真结果表明文中算法在强期望信号功率、低采样快拍数或是存在相干干扰信号的情况下都可以获得较稳定的波束图,具有比极化MVDR算法更优的滤波性能。
[1] Wong K T,Yuan X.Vector cross-product direction-finding with an electromagnetic vector-sensor of six orthogonally oriented but spatiallynoncollocating dipoles or loops[J].IEEE Transactions on Signal Processing,2011,59(1):160-171.
[2] 任燕飞,张云,曾浩,等.新型宽带数字多波束相控阵天线设计[J].电讯技术,2013,53(7):932-937.
REN Yan-fei,ZHANG Yun,ZENG Hao,et al.Design of a Novel Wideband Digital Multi-beam Phased Array Antenna[J].Telecommunication Engineering,2013,53(7):932-937.(in Chinese)
[3] 徐振海,王雪松,肖顺平,等.极化敏感阵列滤波性能分析:完全极化情形[J].电子学报,2004,32(8):1310-1313.
XU Zhen-hai,WANG Xue-song,Xiao Shun-ping,et al.Filtering Performance of Polarization Sensitive Array:Completely Polarized Case [J].Acta Electronica Sinica.2004,32(8):1310-1313.(in Chinese)
[4] 徐友根,刘志文,龚晓峰.极化敏感阵列信号处理[M].北京:北京理工大学出版社,2013:24-26.
XU You-gen,LIU Zhi-wen,GONG Xiao-feng.Signal processing of polarization sensitive array[M].Beijing:Beijing Institute of Technology Press,2013:24-26.(in Chinese)
[5] Nehorai A,Ho K C,Tan B T G.Minimum-noise-variance beamformer with an electromagnetic vector sensor[J].IEEE Transactions on Signal Processing,1999,47(3):601-618.
[6] Xu Y G,Liu T,Liu Z W.Output SINR of MV beamformer with one EM vector sensor of and magnetic noise power[C]//Proceedings of 2004 IEEE 7th International Conference on Signal Processing.Beijing:IEEE,2004:419-422.
[7] Tao J W,Chang W X.A Novel CombinedBeamformer Based on Hypercomplex Processes[J].IEEE Transactions on Aerospace and Electronic Systems,2013,49(2):1276-1289.
[8] 郭玉华,常青美,余道杰,等.一种改进的极化域-空域联合的自适应波束形成算法[J].电子学报,2012,40(6):1279-1283.
GUO Yu-hua,CHANG Qing-mei,YU Dao-jie,et al.An improved Polarization-Space Adaptive Beamforming Algorithm[J].Acta Electronica Sinica,2012,40(6):1279-1283.(in Chinese)
[9] Li H,Li J,Stoica P.Performance analysis of forward-backward matched-filterbank spectral estimators[J].IEEE Transactions on Signal Processing,1998,46(7):1954-1966.
[10] Russell D J,Palmer R D.Application of APES to adaptive arrays on the CDMA reversechannel[J].IEEE Transactions on Vehicular Technology,2004,53(1):3-17.
[11] Jakobsson A,Stoica P.On the forward-backward spatial APES[J].Signal Processing,2006,86(4):710-715.

