多站测向定位新算法
宋文彬,马 霞
(中国西南电子技术研究所,成都 610036)
1 引 言
测向定位是一种非常典型的无源定位手段,它因具有接收隐蔽、抗干扰能力强、工程上易于实现等优点而广泛应用于实际定位中。对于由若干个配置在不同位置台站组成的测向网,每个观测站因为可观测性不好通常单独很难对目标进行准确定位[1],往往设置一个中心站根据多个测向站报来的测向数据在地图上进行交会定位及定位误差分析。传统的算法很少考虑测向误差等因素对交会结果的影响,将各站返回的数据等同对待,如针对三站测向定位刘嘉佳等[2]提出将交会出的三角形的内切圆圆心作为定位结果,也有的是用三角形中线交点,或者Steiner点作为定位结果;如果是多于三站,则每次用3条线,再用另外3条线进行定位或者是计算多边形的质心,还有就是采用Pages-Zamora最小二乘定位法解伪线性超定方程,或者是Brown最小二乘定位法假定目标位置至各方位线垂直距离的平方和最小(如徐济仁等[3])等。还有一类研究得比较多的算法考虑了测向误差等因素的影响,如EKF滤波[4]、UKF滤波[5],以及神经网络法[6]等,其基本思想就是在测向时间同步的基础上要求目标状态的一步预测维持不变。本文以多站无源组网为背景,研究在协同跟踪的情况下,对来自于同一目标的所有测向数据进行集中式融合的方法,用来提高对目标的定位和跟踪精度,并通过仿真分析来说明本文研究的有效性和可行性。
2 测向定位方法
图1为三站测向定位示意图。
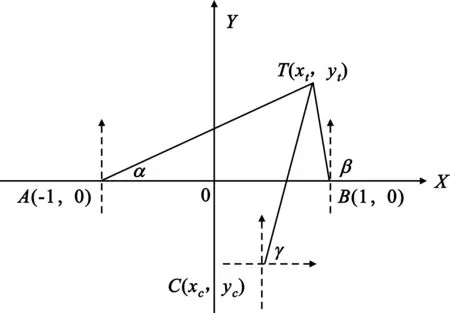
图1 三站测向定位示意图Fig.1 Diagram of cross location with three stations
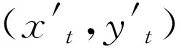
(1)
(2)
其中
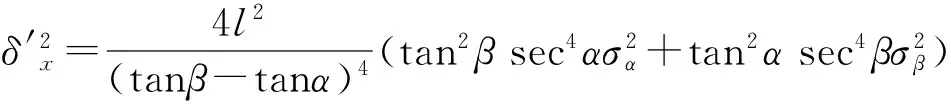
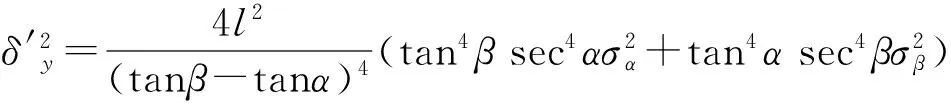
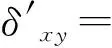
2.1 位置计算
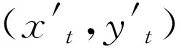
(3)
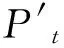
(4)
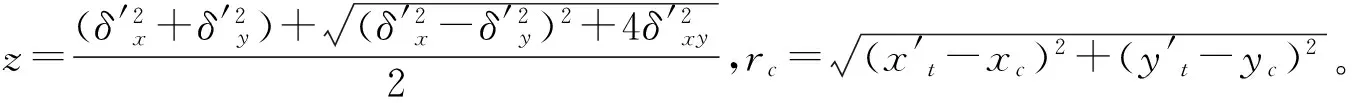
(3)将方位角γ′与观测站C的量测方位角γ进行加权融合,得出目标T相对观测站C的新的方位角γ″:
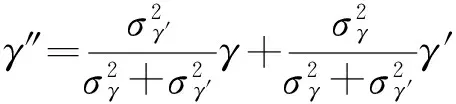
(5)
(4)构造目标位置1的坐标向量X1及其协方差P1与目标位置2的坐标向量X2及其协方差P2。位置1即为由观测站A、B共同确定的目标T的位置,有
(6)
位置2为参考位置1融入观测站C的量测得出的新位置,有坐标向量
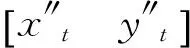
(7)
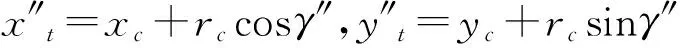
(8)
(5)最后融合估计的目标位置向量XT为位置1和位置2的协方差加权结果,即

(9)
2.2 协方差计算
对于公式(9)中最终位置估计XT的协方差的计算不能直接使用如下简单凸组合式子:
P1(P1+P2)-1P2
(10)
这是因为按照2.1小节的步骤,位置2的得来参考了位置1,它们之间是互相关的,即互协方差不为零,正确协方差求解应采用如下形式:
P1-(P1-P12)(P1+P2-P12-P21)-1(P1-P21)
(11)
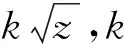
(12)
再使用公式(10)计算得出XT的近似协方差PT,即
PT=P1(P1+P3)-1P3
(13)
3 仿真试验
仿真试验的参数设置如下。A、B、C3个台站的地理位置分别为(-3,0)、(3,0)和(4,-2),目标T的真实位置为(10,2),以上A、B、C3站位置坐标的单位均为km,通过计算得目标相对3个台站所在的真实方位角分别为8.74°、15.94°和33.69°;三站测向的精度均为0.6°,即σα=σβ=σγ≈0.01 rad。蒙特卡罗仿真1 000个时刻,每个时刻3个台站对目标T各测向1次,共测量1 000次。图2(a)给出了1 000个时刻在2.1小节(4)中描述的目标位置向量X1(见加号符号)和X2(见三角形符号),其中X1为每拍利用观测站A和观测站B的量测结果进行联立方程解出的目标分布,X2为每拍参照X1的位置融进观测站C的量测结果得出的目标分布;图2(b)则给出利用公式(9)得出的三站最终融合的目标点迹XT(见菱形符号)。通过左右图的对比,可以发现融合观测站C的量测结果后,目标分布更加集中在其真实位置附近,说明本文提出的位置计算方法切实有效。

(a)目标点迹X1与X2
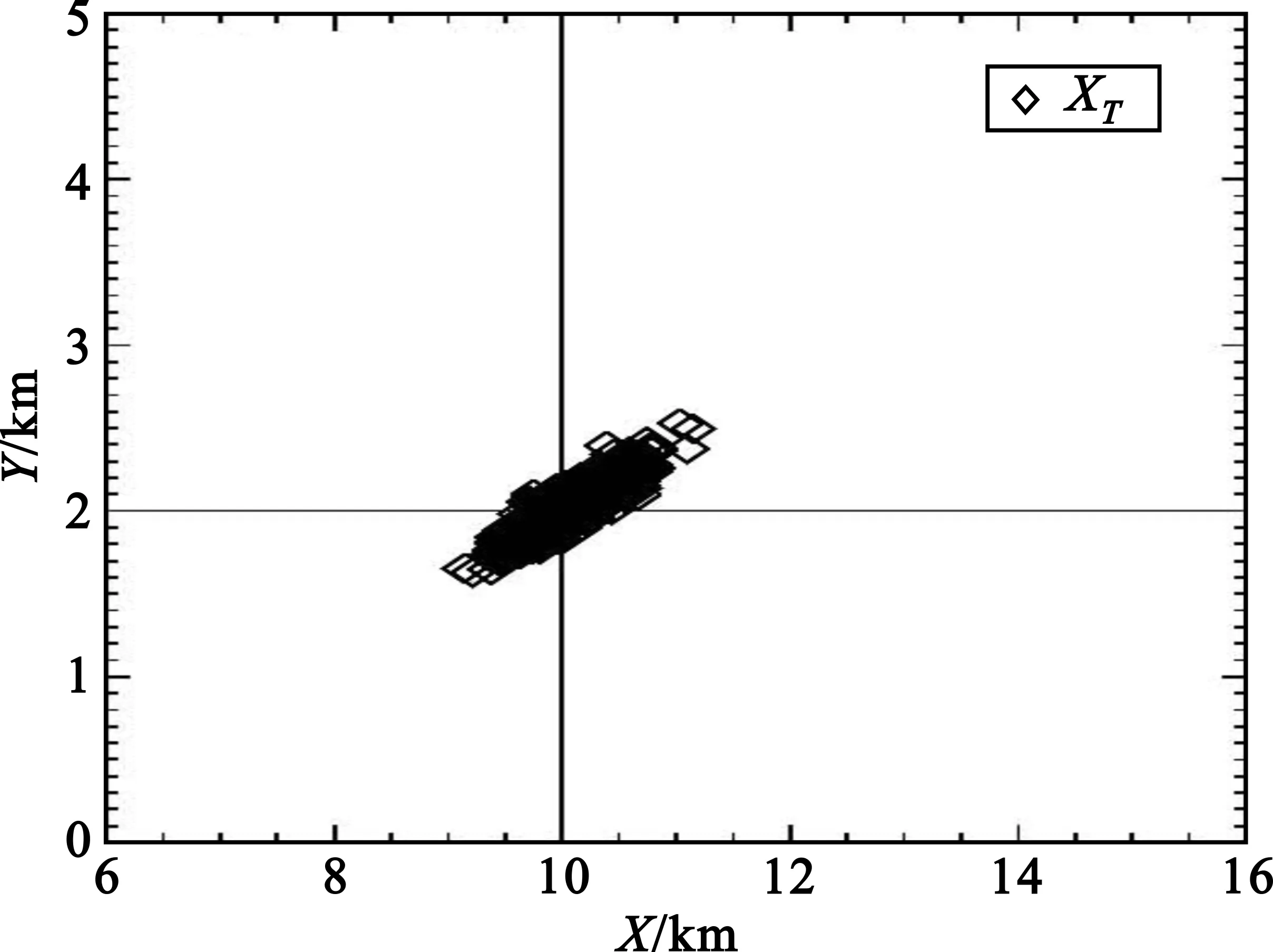
(b)目标点迹XT图2 目标点迹仿真结果Fig.2 The simulated targets′ positions
图3(a)~(c)分别描述的是仿真1 000次计算得到的协方差矩阵PT的左上角、右下角和右上角元素的值(左下角元素值与右上角元素值相等,这里我们取k=100),它们的波动是因为3个观测站每拍的量测值不断变化造成的。图中的水平粗线是统计出的平均值,分别为78 241.4,15 886.0和31 456.1。依据协方差的定义,我们将图2(b)中的1 000个目标点迹XT(xt,yt)做如下统计:
(14)
(15)
(16)
其中n=1 000,所得结果分别为80 075.9,16 829.9和33 044.4。可见它们与图3所示曲线的平均值差距均在10%以内,因此充分说明了本文提出的协方差计算方法也是有效的。
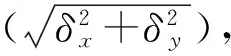
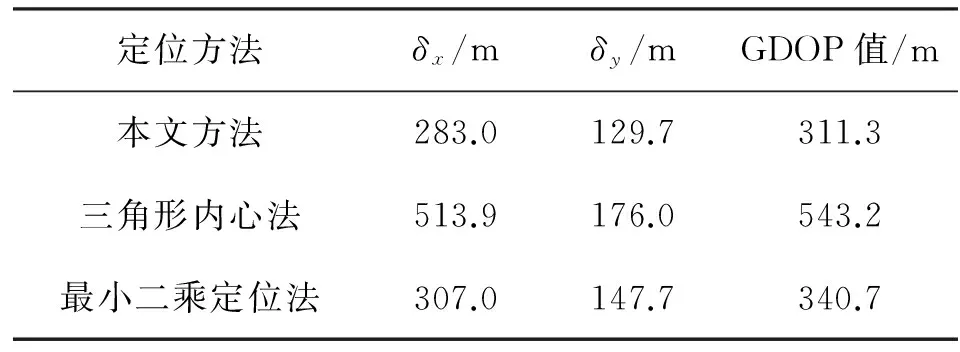
表1 3种算法的定位误差Table 1 The location precision of three algorithms
4 结束语
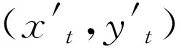
[1] Nordone S,Lindgren A.Fundamental properties and performance of conventional bearings only target motion analysis[J].IEEE Transactions on Automatic Control,1984,29(9):775-787.
[2] 刘嘉佳,龚晓峰,杨建军,等.基于测向定位的算法研究[J].现代电子技术,2004,27(4):49-51.
LIU Jia-jia,GONG Xiao-feng,YANG Jian-jun,et al.Algorithm research based on DF and location [J].Modern Electronic Technology,2004,27(4):49-51.(in Chinese)
[3] 徐济仁,薛磊.最小二乘方法用于多站测向定位的算法[J].电波科学学报,2001,16(2):227-230.
XU Ji-Ren,XUE Lei.LS algorithm used in DF and locatation [J].Chinese Journal of Radio Science,2001,16(2):227-230.(in Chinese)
[4] Song T,Speyer J.A stochastic analysis of a modified gain extended Kalman filter with application to estimation with bearing-only measurement [J ].IEEE Transactions on Automatic Control,1985,30(10):940-949.
[5] 李杰奇,张安,孔福.多传感器测向定位方法研究[J].火力与指挥控制,2009,34(10):62-65.
LI Jie-qi,ZHANG An,KONG Fu.The study on bearing-only multi-sensor location method [J].Fire Control & Command Control,2009,34(10):62-65.(in Chinese)
[6] 罗争,张旻.基于径向基神经网络的空间目标测向定位算法[J].探测与控制学报,2011,33(3):29-33.
LUO Zheng,ZHANG Min.Spacial target bearing-only location algorithm based on RBF neural network [J].Journal of Detection & Control,2011,33(3):29-33.(in Chinese)
[7] 宋文彬.无源雷达协同定位精度分析[J].中国电子科学研究院学报,2012,7(3):294-297.
SONG Wen-bin.The analysis of coordinated oositioning accuracy of passive radars [J].Journal of China academy of Electronics and Information Technology,2012,7(3):294-297.(in Chinese)
[8] 宋文彬.差异维度传感器数据融合新方法[J].电讯技术,2013,53(3):28-32.
SONG Wen-bin.A new data fusion algorithm for sensor measurements of different dimensions [J].Telecommunication Engineering,2013,53(3):28-32.(in Chinese)

