容积Rauch-Tung-Striebel平滑器

杨峻巍

(中国西南电子技术研究所，成都 610036)

1 引 言

在系统状态估计理论中，根据状态向量与观测向量在时间上存在的不同对应关系，人们往往将其归纳为三类估计问题，即状态的预测、滤波和平滑[1]，其中最为经典的状态估计理论为1960年卡尔曼所提出的卡尔曼(Kalman)滤波理论，现已在各种工程中得到了广泛应用。然而标准Kalman理论也有它自身的不足，其要求系统有必须满足以下3个约束条件，即系统模型精确已知、系统的过程噪声和观测噪声为方差已知的白噪声序列以及系统必须为线性随机系统。针对系统模型的不确定性，人们提出了各种自适应滤波算法，如强跟踪滤波算法、鲁棒滤波算法以及基于噪声估计的Sage-Husa自适应滤波算法等。

与此同时，由于在工程实践中，实际系统总是存在不同程度的非线性，如飞机和舰船的惯导系统、火箭的制导与控制系统、目标跟踪以及卫星轨道/姿态的估计系统等都属于非线性滤波问题[2-5]。对于上述系统的状态估计，若采用线性Kalman滤波对其进行滤波估计，则必将导致滤波的发散。为此，一些学者提出了扩展Kalman滤波(Extended Kalman Filter,EKF)，该滤波算法的基本思想是将非线性系统线性化，然后应用Kalman滤波技术进行状态估计，其优点是：计算量小，且能够很好地满足弱非线性系统的状态估计；其不足是：需计算Jacobi矩阵，对于维数较高的系统其计算量较大，对于某些系统甚至无法求取Jacobi矩阵；此外，对于强非线性系统，该滤波算法收敛速度较慢，甚至发散。针对EKF的上述不足，一些学者基于近似非线性函数的概率密度分布比近似非线性函数更容易的思想，提出的Sigma点卡尔曼滤波算法，其中包括Julier和Uhlman提出的无迹卡尔曼滤波(Unscented Kalman Filter，UKF)以及Norgaard和Ito提出的中心差分卡尔曼滤波(Central Differernce Kalman Filter，CDKF)[6-8]。

随着非线性滤波算法研究的不断深入，2009年Simon Haykin提出了一种新的非线性滤波算法，即容积卡尔曼滤波(Cubature Kalman Filter，CKF)，相比于Sigma点卡尔曼滤波算法，该滤波算法不仅计算量相对较小，且对于维数较高的强非线性系统，其滤波性能更优[9-11]。

目前针对非线性系统状态估计的研究，更多的是倾向于滤波算法的研究，而对于状态平滑的问题研究甚少。众所周知，状态平滑由于其利用了更多的观测信息而使得其比滤波算法具有更精确的状态估计效果，因此在现实工程实践中得到了广泛的应用，如导弹发射初始速度的估计、卫星轨道重构以及雷达目标跟踪等等[12-14]。

为此，本文基于非线性系统最优平滑算法建立了容积Rauch-Tung-Striebel平滑器。首先，详细推导了基于概率密度分布形式的非线性系统最优平滑算法，并给出了基于Rauch-Tung-Striebel理论的最优平滑迭代算法；然后将其与容积卡尔曼滤波理论相结合建立了容积Rauch-Tung-Striebel平滑器；最后对其可行性及有效性进行了仿真实例证明。

2 问题描述

不失一般性，考虑如下的非线性系统状态空间模型：

(1)

其中：xk∈Rn，yk∈Rm分别为系统状态向量与量测向量；wk-1，vk分别为系统噪声和量测噪声，它们是相互独立的高斯白噪声，且分别满足wk-1～N(0,Qk)，vk-1～N(0,Rk)；初始状态x0与wk-1，vk互不相关，且满足x0～N(m0,P0)；fk-1(·)，hk(·)分别表示非线性系统的系统函数与量测函数。

基于贝叶斯估计理论框架下的非线性系统平滑器，其本质目的就是利用量测值y1:T={y1,y2,…,yT}获取平滑分布p(xk|y1:T)的最优或次优近似，且其分布近似满足高斯分布，即

(2)

3 非线性系统状态最优平滑算法

3.1 非线性系统最优滤波算法

在贝叶斯状态估计理论框架下，由式(1)表示的系统状态空间模型，也可表示为如下的所示的概率密度分布形式，即

(3)

其中，p(xk|xk-1)表示系统状态转移概率密度,p(yk|xk)表示量测值的似然概率密度。

基于上述系统概率密度模型，其最优滤波迭代算法可表示为时间更新和量测更新两个基本步骤。

(1)时间更新

(4)

(2)量测更新

p(xk|y1:k)=Cp(yk|xk)p(xk|y1:k-1)

(5)

其中，C为归一化因子，其具体表达式如下所示：

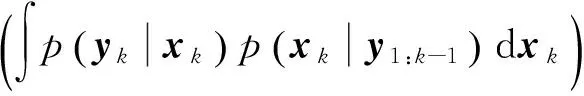
(6)

3.2 非线性系统最优平滑算法

根据文献[12]可知，上述非线性系统状态空间模型的最优平滑算法，可写为如下两种形式，且两者理论上相互等价。

形式1 两滤波平滑算法

该平滑算法可表示为如下的概率密度分布函数：

p(xk|y1:T)∝p(xk|y1:k)p(yk+1:T|xk)

(7)

其中，右边第一项可通过最优滤波算法进行实现,第二项则可用一反向滤波算法来实现。

形式2 前向-后向平滑算法

该平滑算法可表示为如下的概率密度分布函数：

p(xk|y1:T)=p(xk|y1:k)×

(8)

其中，p(xk|y1:k)表示当前时刻状态的滤波概率密度分布,p(xk+1|y1:k)表示k+1时刻状态的预测概率密度分布。

3.3 非线性系统RTS平滑算法

为了建立非线性系统RTS平滑算法，将式(8)分解为以下三个步骤：

步骤1：建立y1:k条件下xk与xk+1的联合概率密度函数：

p(xk,xk+1|y1:k)=p(xk+1|xk)p(xk|y1:k)

(9)

其中，p(xk|y1:k)表示当前时刻的滤波概率密度分布；

步骤2：计算xk+1和y1:k条件下xk的概率密度函数：

(10)

其中

(11)

由于系统状态空间模型具有马尔科夫特性，因此有p(xk|xk+1,y1:T)=p(xk|xk+1,y1:k)，则可得

(12)

步骤3：计算y1:T条件下xk与xk+1的联合概率密度函数：

p(xk,xk+1|y1:T)=p(xk|xk+1,y1:T)p(xk+1|y1:T)

(13)

其中,p(xk+1|y1:T)表示下一时刻的平滑分布。因此在xk+1边缘化条件分布下，xk的平滑概率密度函数可表示为

(14)

3.4 非线性系统RTS平滑算法概率密度函数近似

假设1 状态滤波的概率密度函数服从高斯分布，即

p(xk|y1:k)≈N(xk|mk,Pk)

(15)

假设2k+1时刻状态平滑的概率密度函数服从高斯分布，即

(16)

根据上述两个基本假设对3.3小节推导的非线性系统最优RTS平滑算法进行概率密度函数近似。

(1)对式(9)中的xk、xk+1联合分布进行高斯近似，则可得

(17)

(18)

(2)根据高斯分布准则及式(17)，则式(12)也近似服从高斯分布，即

(19)

其中：

(20)

(21)

(22)

(3)根据假设2，则式(13)近似服从高斯分布，即

(23)

其中：

(24)

(25)

则可得k时刻状态平滑服从高斯分布，即

(26)

其中：

(27)

(28)

4 容积RTS平滑算法

4.1 CKF基本原理

CKF的基本思想是，基于高斯域贝叶斯状态估计理论框架，将非线性滤波归结为“非线性函数×高斯概率密度”的积分问题，即

(29)

其中，x表示待估系统状态向量，f(x)表示求积非线性函数，Rn表示积分区间。

针对形如式(29)的积分问题，CKF滤波算法采用3自由度Spherical-Radial求容积规则，采用2n个等权值的容积点来实现非线性逼近，即

(30)

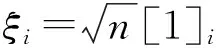
(31)

4.2 CKF迭代算法

针对形如式(1)的系统状态空间模型，利用4.1小节所述的CKF基本原理，即可推导出CKF的迭代滤波算法，其包括时间更新和量测更新两个基本步骤。

(1)时间更新

(32)

(33)

(34)

(35)

(36)

(2)量测更新

(37)

(38)

Yi,k|k-1=H(Xi,k|k-1)

(39)

(40)

(41)

(42)

(43)

(44)

(45)

4.3 容积CTS平滑算法

将上述非线性系统RTS平滑算法与标准CKF滤波算法进行有机结合，即可得容积RTS平滑算法的递推迭代算法，其具体过程包括四个步骤。

(1)建立容积点

(46)

其中

(47)

(2)通过系统状态模型传播容积点

(48)

(3)计算系统状态的预测值、预测协方差矩阵及互协方差矩阵

(49)

(50)

(4)通过系统状态模型传播容积点

(51)

(52)

(53)

5 仿真实例

为了验证容积Rauch-Tung-Striebel平滑器的有效性，下边通过一典型非线性系统模型对其进行仿真分析，该系统模型为纯方位目标跟踪模型，其状态方程为

(54)

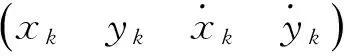
(55)

其中q表示噪声谱密度，这里假设q=0.1。

其量测模型为

(56)

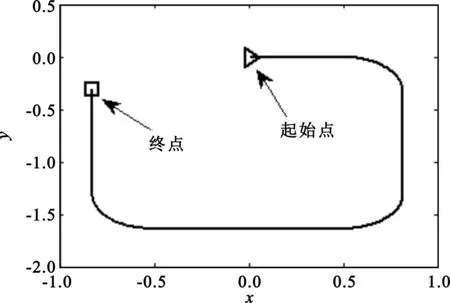
图1 运动目标真实轨迹Fig.1 The real trajectory of the moving object

同时取状态估计的初始值为

分别采用EKF、UKF、CKF及相应的RTS平滑算法对其进行仿真验证，图2～5分别表示采用标准CKF滤波算法与RTS-CKS平滑算法对运动目标4个运动状态的实时估计，由仿真结果可以直观地看出，RTS-CKS平滑算法对目标状态的估计精度明显优于标准CKF滤波算法，这充分验证了RTS-CKS平滑算法相对于标准的CKF滤波算法在提高状态估计精度和解决非线性系统状态平滑问题等方面的有效性和可行性。

图3 运动目标在y方向上的位置估计Fig.3 The y-direction position estimation of the moving object

图4 运动目标在x方向上的速度估计Fig.4 The x-direction velocity estimation of the moving object

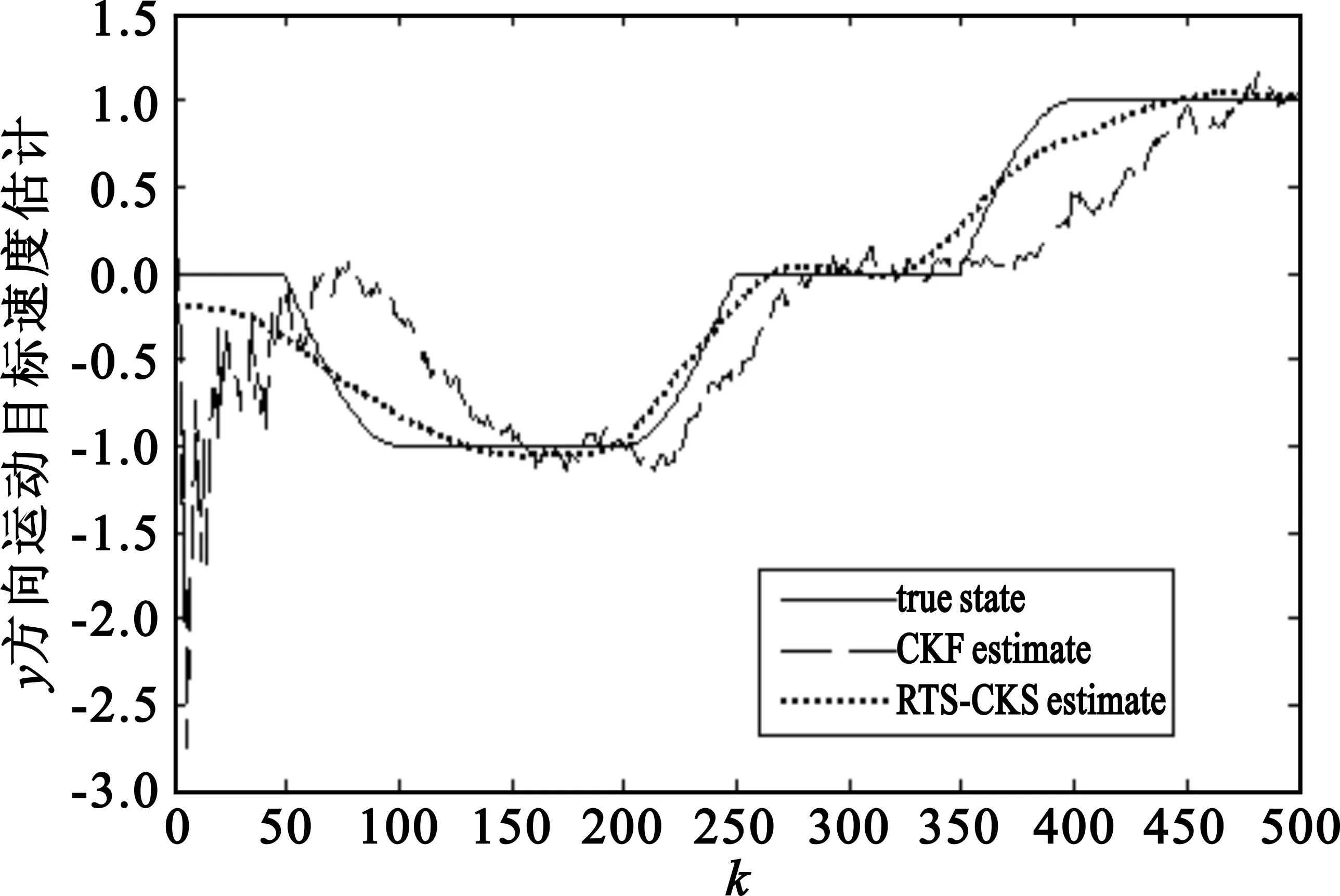
图5 运动目标在y方向上的速度估计Fig.5 The y-direction position estimation of the moving object

图6～8分别表示EKF、UKF、CKF及相应的RTS平滑算法对运动目标的轨迹跟踪，不难看出，各种非线性滤波算法的RTS平滑算法对轨迹的跟踪精度明显优于对应的非线性滤波算法本身。

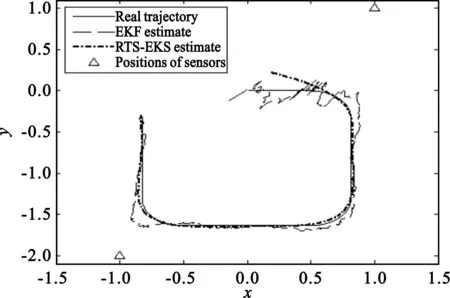
图6 EKF及RTS-EKS运动目标轨迹跟踪Fig.6 The trajectory tracking of the moving object with EKF and RTS-EKS

图7 UKF及RTS-UKS运动目标轨迹跟踪Fig.7 The trajectory tracking of the moving object with UKF and RTS-UKS

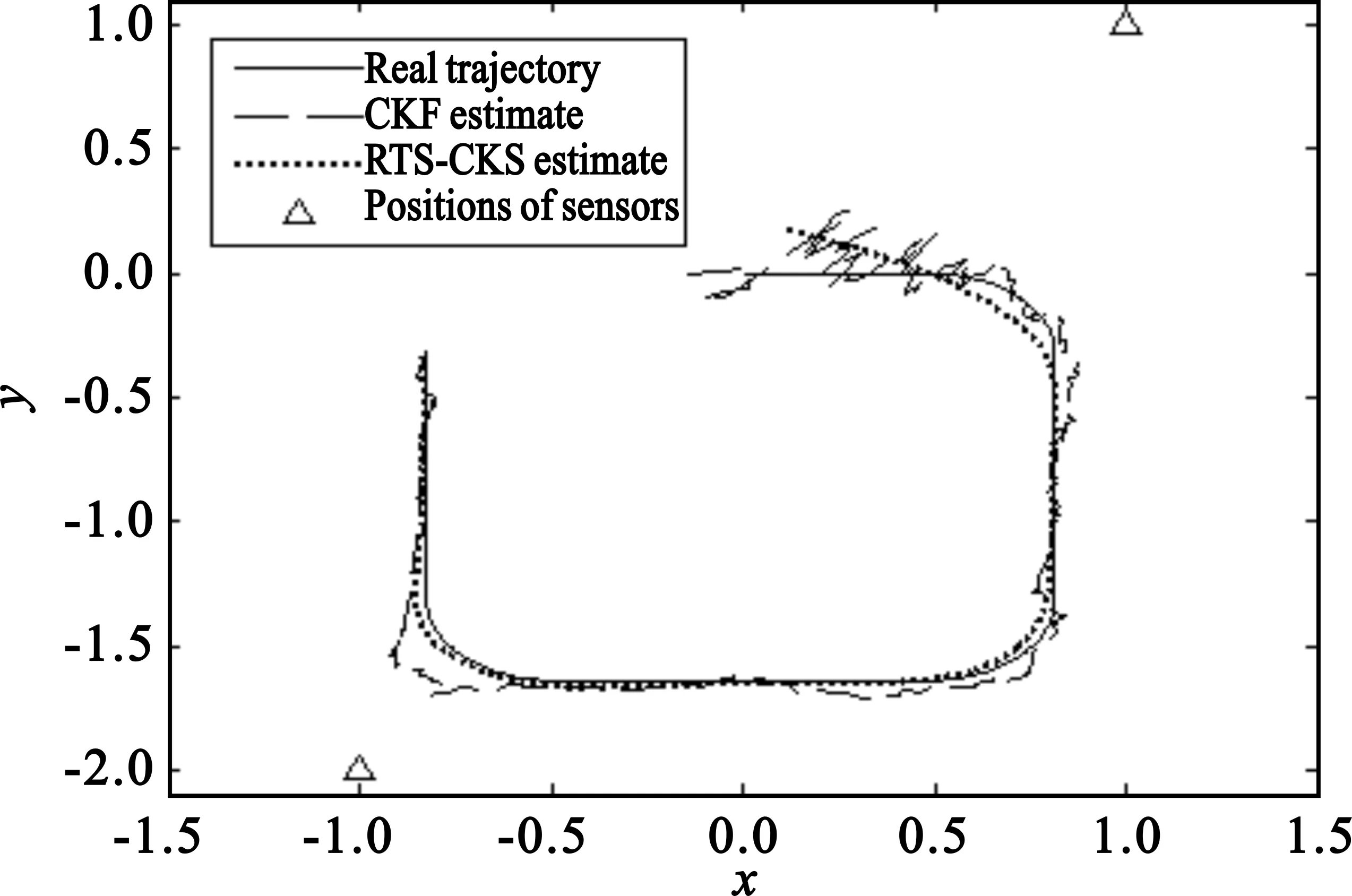
图8 CKF及RTS-CKS运动目标轨迹跟踪Fig.8 The trajectory tracking of the moving object with CKF and RTS-CKS

各种滤波算法及相应的平滑算法估计均方误差如表1所示。

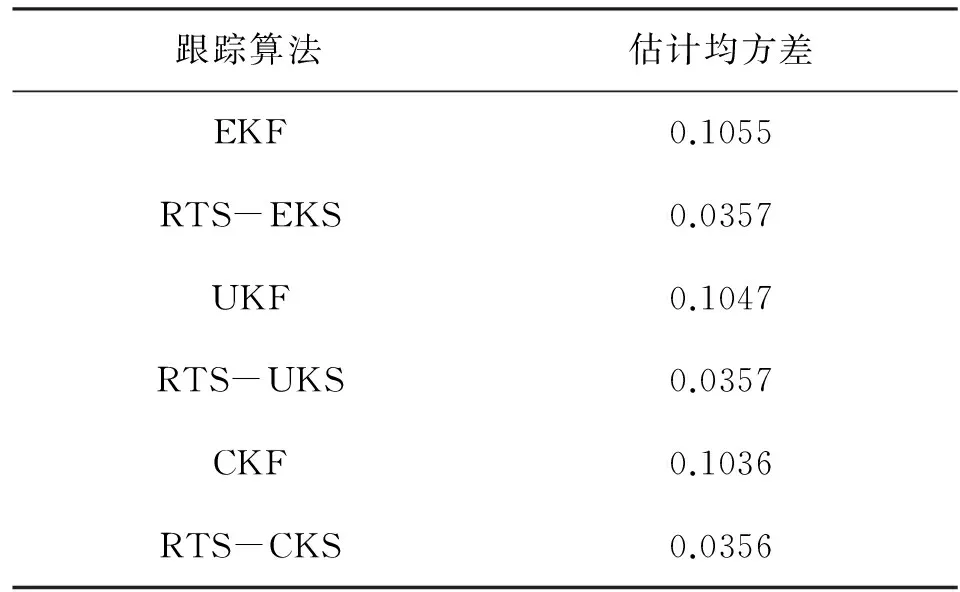
表1 各种滤波算法及相应的平滑算法估计误差Table 1 The estimation error of the filtering methods and corresponding smoothing algorithm

由表1的统计结果可以看出，UKF的目标跟踪精度优于EKF ，而CKF的目标跟踪精度优于UKF，且RTS-CKS的目标轨迹跟踪精度也是最佳的，这充分说明了RTS-CKS相比于其他两种平滑算法在解决非线性状态的平滑估计问题时的优越性。

6 结 论

本文基于贝叶斯估计理论框架推导了非线性系统RTS平滑算法，并将其与容积卡尔曼滤波相结合，建立了容积Rauch-Tung-Striebel平滑器；相比于RTS-EKS，该平滑算法无需计算复杂的雅克比矩阵，且没有进行一阶线性化，因此状态估计精度较高；相比于RTS-UKS，该平滑算法无需预先设定一些相关参数，且在系统维数较高的条件下，估计精度稍高，此外采样点也略有减少，因而其计算量也会相应有所减小。仿真结果表明，所建立的RTS-CKS平滑算法为解决非线性系统的状态平滑问题提供一种切实可行的方案，且相比于EKF、UKF等非线性滤波算法及其平滑算法在估计精度上具有一定的优越性。为了提高其工程实用性，今后需对其计算复杂度开展进一步的研究。

[1] 付梦印,邓志红,张继伟.Kalman滤波理论及其在导航系统中的应用[M].北京:科学出版社,2009.

FU Meng-yin,DENG Zhi-hong,ZHANG Ji-wei.Kalman filtering theory and its application in the navigation system[M].Beijing:Science Press,2009.(in Chinese)

[2] R van der Merwe.Sigma-point Kalman filters for probabilistic inference in dynamic state-space models[D].Portland,OR,USA:OGI School of Science & Engineering at Oregon Health & Science University,2004.

[3] 魏喜庆,宋申民.基于容积卡尔曼滤波的卫星姿态估计[J].宇航学报,2013,34(2):394-200.

WEI Xi-qing,SONG Shen-min.Cubature Kalman Filter-Based Satellite Attitude Estimation[J].Journal of Astronautics,2013,34(2):394-200.(in Chinese)

[4] Pesonen H,Piche R.Cubature-based Kalman filters for positioning[C]//Proceedings of 2010 IEEE International workshop on Positioning,Navigation and Communication.Dresden:IEEE,2010:45-49.

[5] 鹿传国,冯新喜,张迪.基于改进容积卡尔曼滤波的纯方位目标跟踪[J].系统工程与电子技术,2012,34(1):28-33.

LU Chuan-guo,FENG Xin-xi,ZHANG Di.Pure bearing tracking based on improved cubature kalman filter[J].Systems Engineering and Electronics,2012,34(1):28-33.(in Chinese)

[6] Julier S J,Uhlmann J K.Unscented Filtering and Nonlinear Estimation[J].Proceedings of the IEEE,2004,92(3):401-422.

[7] 宋勇,胡波,李在清.基于平方根无迹卡尔曼滤波的数字预失真算法[J].电讯技术，2011,51(11):20-24.

SONG Yong,HU Bo,LI Zai-qing.A Novel Digital Predistortion Algorithm Baesd on Square Root Unscented Kalman Filter[J].Telecommunication Engineering,2011,51(11):20-24.(in Chinese)

[8] 王小旭,潘泉,程咏梅,等.中心差分卡尔曼平滑器[J].控制理论与应用,2012,29(3):361-367.

WANG Xiao-xu,PAN Quan,CHENG Yong-mei,et al.Central difference Kalman smoother [J].Control Theory & Applications,2012,29(3):361-367.(in Chinese)

[9] Arasaratnam I，Haykin S.Cubature Kalman Filters [J].IEEE Transactions on Automatic Control,2009,54(6):1254-1269.

[10] Arasaratnam I,Haykin S,Hurd T R.Cubature Kalman Filtering for Continuous-Discrete Systems:Theory and Simulations[J].IEEE Transactions on Signal Processing,2010,58(10):4977-4993.

[11] 孙枫,唐李军.Cubature卡尔曼滤波与Unscented卡尔曼滤波估计精度比较[J].控制与决策,2013,28(2):304-308.

SUN Feng,TANG Li-jun.Estimation precision comparison of Cubature Kalman filter and Unscented Kalman filter[J].Control and Decision,2013,28(2):304-308.(in Chinese)

[12] Simo S.Unscented Rauch-Tung-Striebel Smoother [J].IEEE Transactions on Automatic Control,2008,53(3):845-848.

[13] Saifudin R,Keigo W,Shoichi M,et al.An Unscented Rauch-Tung-Striebel Smoother for a Bearing Only Tracking Problem[C]//Proceedings of 2010 IEEE International Conference on Control,Automation and Systems.Gyeonggi-do:IEEE,2010:1281-1286.

[14] Deisenroth M P,Turner R D,Huber M F,et al.Robust Filtering and Smoothing with Gaussian Processes[J].IEEE Transactions on Automatic Control,2012,57(7):1865-1871.