基于时间序列-因果关系结合法的中国海港集装箱吞吐量中长期预测

朱小檬，栾维新，朱义胜

(大连海事大学a.马克思主义学院;b.交通运输管理学院;c.信息科学技术学院，辽宁 大连 116026)

交通运输是国民经济和社会发展的重要基础。集装箱运输以其高效、便捷、安全的特点成为交通运输现代化的重要形式。集装箱港口质量的好坏影响到对外运输成本，关系到外国直接投资(FDI)流入的数量。优质的港口基础设施会产生积聚效应，形成全球型或者区域性航运中心。目前我国集装箱港口之间的竞争日益激烈。由于集装箱港口具有建设资金投入量大、建设周期长的特点，盲目追求发展枢纽港的热潮将造成巨大的浪费。因此预测我国港口集装箱中长期(至2020年)吞吐量对我国港口合理布局和规划具有重要意义。

目前预测港口集装箱吐量的方法大致可分为两大类［1］:一类是时间序列分析法;另一类是因果关系法。时间序列分析法是依据海港集装箱吞吐量的历史变化数据，建立数学模型，找出其随时间变化的规律进行预测。因果分析法则主要是依据腹地的各种社会经济指标，找出这些指标与集装箱吞吐量的关系，然后再根据这些社会经济指标的变化，预测港口集装箱吞吐量。上述两类方法在中长期集装箱吞吐量预测时，都遇到了困难。本文把二者结合起来，提出集装箱吞吐量中长期预测的时间序列-因果关系结合法。结合法用GDP 取代时间作为解释变量。本文没有分别进行GDP 各要素与集装箱吞吐量之间的多变量拟合关系的研究，原因是我国海港集装箱运输业发展是GDP 各要素共同作用的结果，GDP各要素之间存在很大的相关性，难以确定各要素对集装箱运输业发展影响的主成分，而GDP 恰恰又是国民经济各要素之共同计算的结果。

为了克服利用GDP 数据取代时间作解释变量对非线性曲线带来的不稳定性，分别对集装箱吞吐量时间序列和GDP 时间序列取自然对数，然后采用HP 滤波器(the Hodrick-Prescott filter)，合理选择滤波因子［2］，滤除时间序列的波动分量，用GDP 时间序列的趋势分量拟合集装箱吞吐量时间序列的趋势分量，建立GDP 时间序列与集装箱吞吐量时间序列之间的因果关系式。

一、GDP 与海港集装箱吞吐量因果关系的建立

改革开放30 多年来，我国GDP 呈指数形式增长［3］，我国海港集装箱运输业也是从无到有呈指数形式发展［4］。受到国际环境变化和宏观经济发展规律的影响，两条宏观经济时间序列存在波动(参见图1)，在建立GDP 时间序列与海港集装箱吞吐量时间序列之间的因果关系时，利用数字分析技术直接拟合这两条非线性曲线是困难的。为此，分别对两条宏观经济时间序列取自然对数:

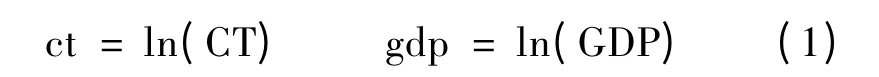
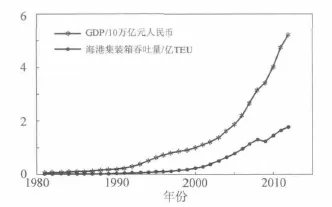
图1 中国GDP 和港口集装箱吞吐量曲线

然后利用HP 滤波器滤出波动分量，获得我国海港集装箱吞吐量和我国GDP 时间序列的趋势分量，在Matlab 平台上，进行HP 滤波的语句是

式中:ct 和gdp 分别代表取自然对数的我国海港集装箱吞吐量时间序列和GDP 时间序列;tc 和tg 分别代表它们的趋势分量。以上运算只有一个参数λ 需要确定，对于短时间序列，既保持时间序列的变化趋势，又含有一定的波动信息，本文选择λ =6.8［2］。计算结果说明，λ 的选择会直接影响以后曲线拟合的结果。取自然对数和经过HP 滤波后的我国海港集装箱吞吐量和我国GDP 时间序列的趋势分量如图2所示。

图2 中国GDP 和港口集装箱吞吐量的趋势分量

在对数域进行海港集装箱吞吐量和GDP 关系的拟合，如果拟合收敛，可以写做

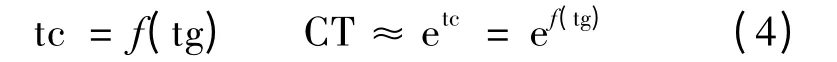
式(3)决定海港集装箱吞吐量将是GDP 的复杂的指数函数，该函数使两条曲线拟合更加容易。在以下拟合过程，还要解决下列问题:确定拟合多项式的阶数，确定拟合区间和确定解释变量合理的变化范围。因为以上因素都影响海港集装箱吞吐量预测的结果。

二、t 检验和拟合多项式阶数的确定

为叙述方便，令yi=cti，xi=tgi，利用对数域的GDP 趋势分量拟合我国海港集装箱吞吐量的趋势分量的多项式可以写成:

定义其系数矩阵:

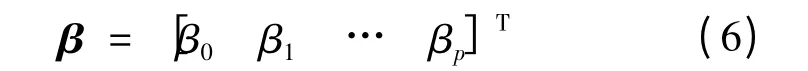
结构矩阵:

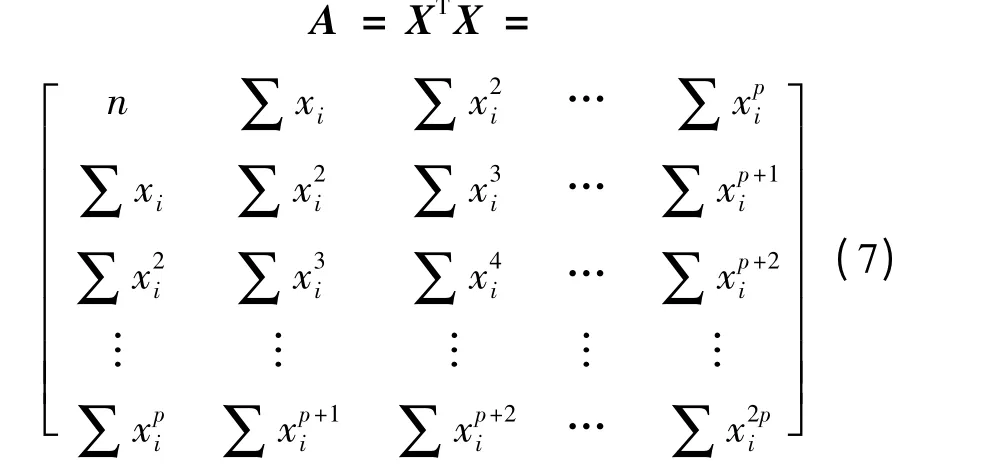
式中:

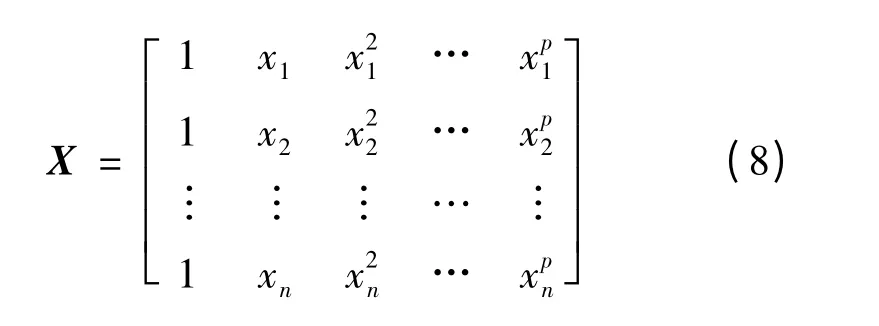
常数矩阵:

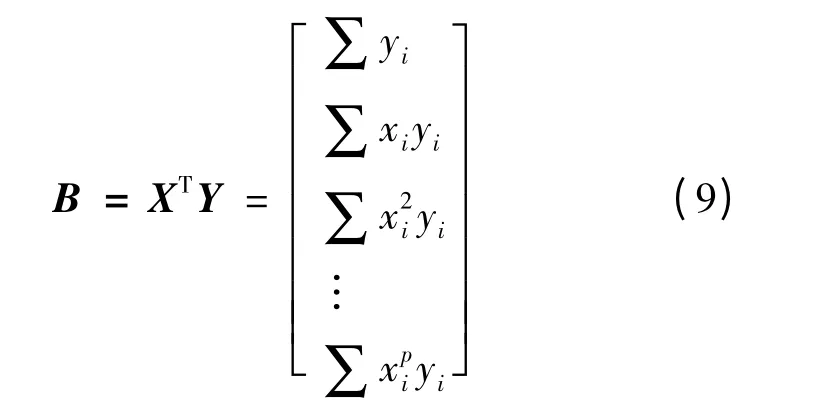
回归方程系数的最小二乘估计为

求解式(9)的系数是通过Eviews 7.0 软件来完成的。模型(5)是否能是正确的拟合还要求多项式的系数βj(j = 0，1，2，…，p)通过t 检验［5－6］。虽然多项式系数t 检验值也受拟合区间的影响，计算结果显示:4 阶和4 阶以上多项式的系数均不能通过显著性水平(如0.05)对t 值的检验。在1 至3 阶多项式中，参看拟合多项式确定的初始值和曲线走势，本文选用2 阶多项式。

三、Shapley 值权重分配的组合预测

利用GDP 的趋势分量拟合海港集装箱吞吐量的趋势分量，满足t 检验，符合初始值和增长趋势的拟合区间可能有几个，比如:1991—2012年、1993—2012年和1995—2012年3个不同的拟合区间可能产生3个不同的拟合多项式。为了解决不同拟合区间产生不同的预测结果问题，本文采用Shapley值权重分配的组合预测［7］。

组合预测方法是对同一个问题，采用不同预测方法或区间的预测，然后把各种预测结果按一定的权重组合起来。针对本文的问题，不同长度拟合区间可以获得不同的拟合多项式。组合的目的是综合利用适合拟合区间所提供的信息，尽可能地提高预测精度。

假设有n 种预测方法来进行组合预测，记作l ={1，2，…，n}，对于l 的任何子集s，t(表示n 种预测方法中的任一组合)，e(s)、e(t)表示各自组合的误差。定义:

(1)对于l 的任一子集s，t，都有E(s)+E(t)≥E(s ∪t)，E(s)、E(t)、E(s ∪t)为各自预测时产生的误差。

(2)s ⊆l，zi表示第i 种预测方法在合作最终分摊的误差值，总有zi≤E(i)。

(3)对于n 种预测方法参与的组合预测产生的总误差E(n)，将在n 种预测方法之间进行完全分配，即

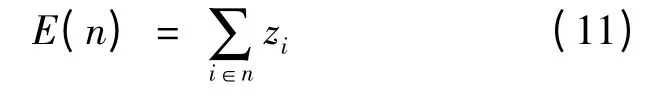
设第i 种预测方法的预测误差的绝对值平均值为Ei，组合预测的总误差为E:

式中:m 是样本的个数;n 是单一预测方法的个数;E是组合预测的预测误差总值。

Shapley 值的分配公式为

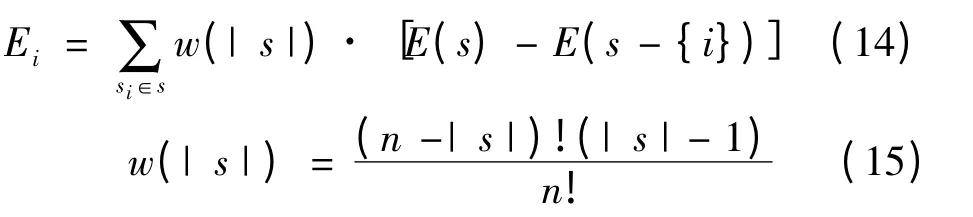
式中:s 包含i 的所有子集;| s| 表示组合中预测模型的个数;n 表示组合预测中预测模型的总个数;w(| s|)是加权因子，表示组合中i 应承担的组合边际贡献;s－{i}表示组合中除去模型i;i 表示组合预测中某一个预测模型;Ei表示i 模型分得的误差量，即Shapley 值。

根据以上的公式确定组合预测中各预测方法的权重，公式为

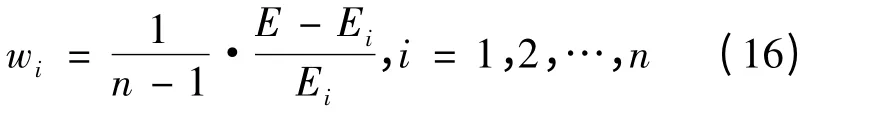
用对数域GDP 趋势分量的二次多项式拟合海港集装箱吞吐量的结果如式(18)～(20)所示。3个拟合区间产生的拟合误差如表1所示。对表1的拟合误差取绝对值后取平均，得到表2各子集误差值。

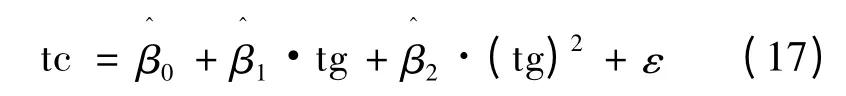
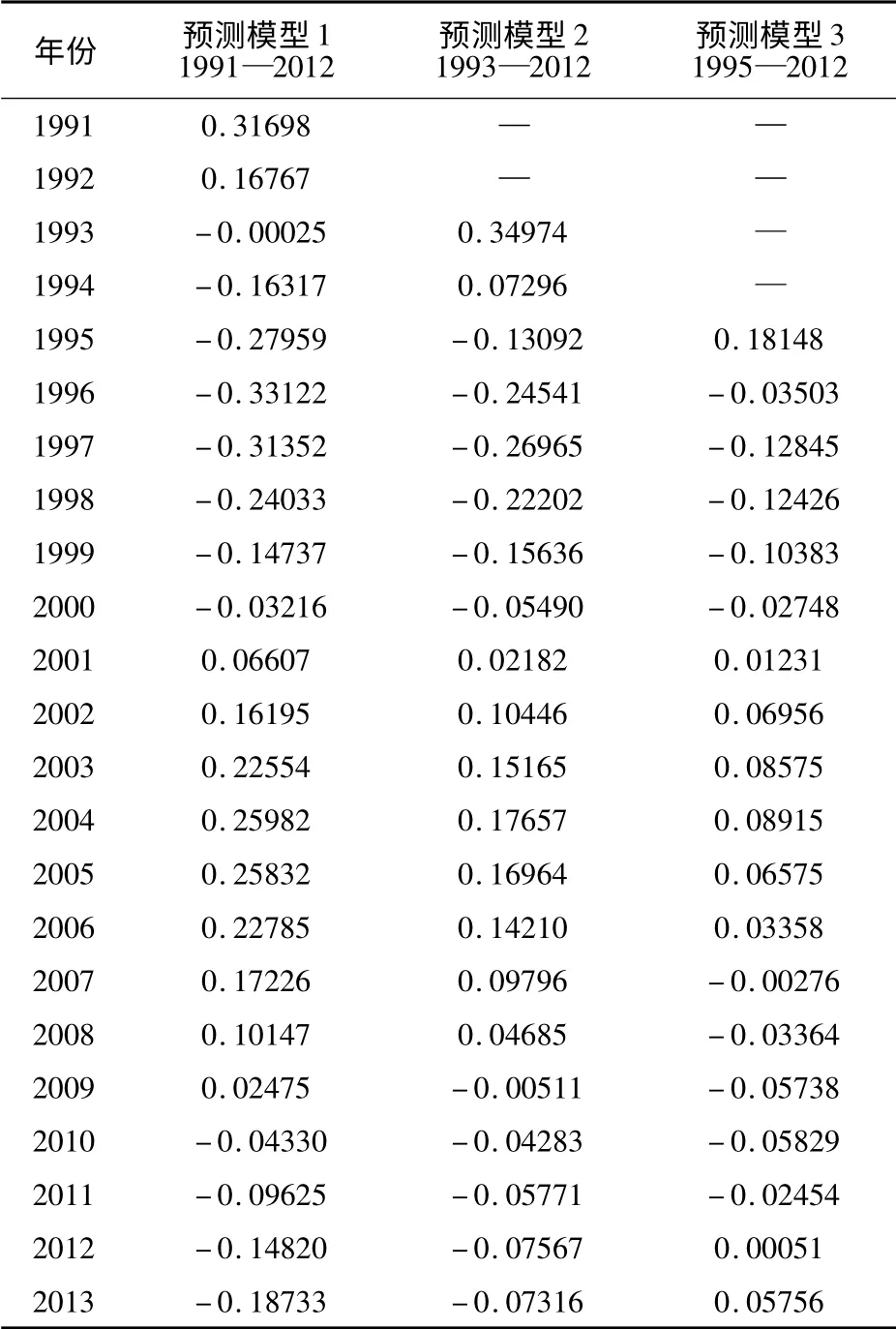
表1 3 种拟合区间的拟合误差

表2 各子集的误差值

Shapley 值为

计算各个预测模型的权重为

利用式(21)～(22)得到组合预测结果可以表示为

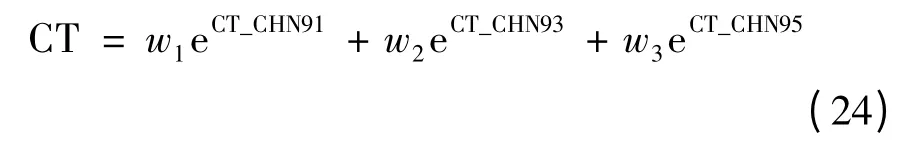
四、GDP 的合理变化区间

在进行集装箱吞吐量中长期预测时，必须确定GDP 的合理变化区间。从国际经验看［8］，二战以后实现成功追赶的一些经济体都经历了20 ～30年的高速增长，在人均GDP 达到11 000 国际元时，几乎无一例外地出现了增长速度的回落，降幅为30%左右。改革开放以来我国经济增长的路径与这些成功追赶型经济体比较接近。根据研究测算，我国人均收入在今后不长时间内将达到11 000 国际元的时间窗口，有可能出现潜在增长率的下降。如图3所示，我国GDP 从2008年已经开始回调。

经过一个时期的调整，即使我国经济增长速度下调到相对较低的水平，比如7% 左右，从国际上看，仍属相当高的增长速度。如果我国能够顺利实现从要素驱动到创新驱动增长模式的转换，将会迎来一个更加注重质量、效益和可持续性的新增长阶段。由于我国需要解决全国每年1000 万人以上新增城镇劳动力的就业问题，还要解决600 万～700 万新增的农村劳动力进城务工问题，我国2014—2020年间GDP 也不能或不可能下降太多。因此，本文把2013—2020年GDP 增长按超常发展每年增长7.5%、适中发展每年增长6.0%和保守估计每年按4.5%增长的区间变化，即

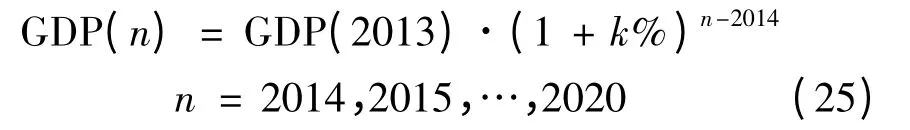
式(25)的结果取自然对数tg(n)= ln(GDP(n))，如表3所示。

如果得到GDP 和海港集装箱吞吐量之间的函数关系式(18)～(20)，把表3中的按不同年增长率下我国GDP 的自然对数代入式(18)～(20)，就可以预测我国海港集装箱吞吐量。计算式(24)是利用Eviews 软件来完成的。

利用时间序列－因果关系法预测中国海港集装箱吞吐量的结果如图4所示。

如果我国GDP年均以7.5%的速度增长，2020年我国海港集装箱吞吐量将达到2.308 亿TEU;如果我国GDP年均以6.0%的速度增长，2020年我国海港集装箱吞吐量将达到2.258 亿TEU;如果我国GDP年均以4.5%的速度增长，2020年我国海港集装箱吞吐量将达到2.195 亿TEU。

表3 按不同年增长率下中国GDP 的自然对数

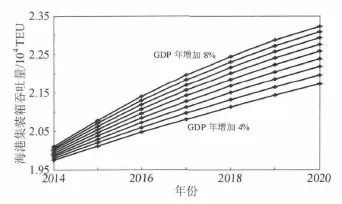
图4 时间序列－因果关系法预测中国海港集装箱吞吐量

五、结 语

本文运用时间序列－因果关系结合法预测我国海港集装箱中长期吞吐量。该方法采用国内生产总值(GDP)作为解释变量，利用多项式回归模型拟合集装箱吞吐量时间序列，形成了GDP 时间序列对集装箱吞吐量序列的因果关系。为了克服预测模型对初始值的敏感性，分别对集装箱吞吐量时间序列和GDP 时间序列取自然对数，在对数域中采用HP 滤波技术，滤除时间序列的波动分量。采用GDP 时间序列的趋势分量拟合集装箱吞吐量时间序列的趋势分量，根据我国工业化进程和全球经济一体化的国际环境，当我国GDP 在合理增长率区间下运行，预测了2013 至2020年我国海港集装箱吞吐量。如果我国GDP年均以6.0%的速度增长，2020年我国海港集装箱吞吐量将达到2.258 亿TEU。

［1］吕靖.海运港口货物吞吐量预测的PHQDF 模型［J］.大连海事大学学报，1995(1):77－79.

［2］朱小檬，朱义胜，栾维新.宏观经济时间序列的频率域特性与HP 滤波器平滑参数的选择［J］.统计与决策，2012(5):7－11.

［3］国家统计局.中国统计年鉴2012［M］.北京:中国统计出版社，2012.

［4］中国港口年鉴编辑委员会.中国港口年鉴2012［M］.北京:中国港口杂志社，2012.

［5］易丹辉.数据分析与Eviews 应用［M］.北京:中国人民大学出版社，2008:32－33.

［6］高铁梅.计量经济分析方法与建模:Eviews 应用及实例［M］.2 版.北京:清华大学出版社，2009:15－16.

［7］董艳，王冠奎.组合预测法在物流需求中的应用［J］.中国储运，2006(5):108－109.

［8］刘世锦.加快经济增长动力结构和机制转换［EB/OL］.(2012－08－22)［2014－03－25］.http://finance.people.com.cn/n/2012/0822/c70846-18800153.html.