对一类和式极限计算公式与方法的改进

陆健

（南通职业大学，南通 226007）

对一类和式极限计算公式与方法的改进

陆健

（南通职业大学，南通 226007）

针对有关一类常见的和式极限计算的研究结果，给出并证明了减弱条件后公式仍然成立的结论；进一步为在实际计算中避免高阶求导的复杂性，给出了幂级数展开、舍去余项的简便计算方法。

和式极限；高阶导数；幂级数；余项

定理设函数f(x)在x=0处m阶可导，且实数p，q满足p＞q≥0或p＞0＞q＞-m-1，记k=（p-q）m-1，则有

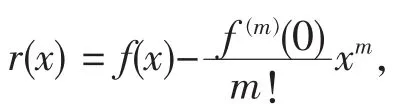
xi=iqn-p（1≤i≤n）。若p＞q≥0，则xi≤nq-p→0(n→∞)；若p＞0＞q＞-m-1，则xi≤n-p→0（n→∞）。

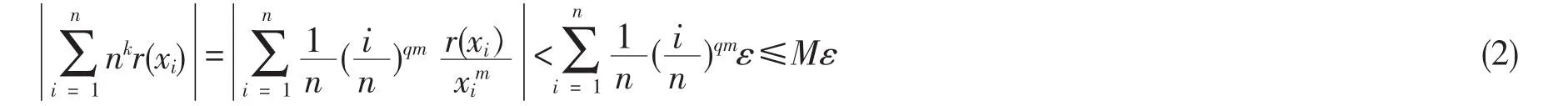
定理得证。

求相关的和式极限可直接套用定理公式，但需引入适当的函数，还要求出非零的导数值，并核对参数p、q、k是否满足条件。

在许多情形下，可引入的函数f(x)并不明显，而且在处x=0不为零的导数阶数m较大，这时直接套用定理公式就会很困难，不仅计算量庞大，而且还显得呆板。定理的实质是利用幂级数展开化简极限式，展开到第一个非零项即可，余项作为高阶无穷小在极限计算中不起作用，可直接舍去。这种展开级数的处理方法较为简便且灵活。

解难以找到适当的函数，只能分项处理。用级数展开法则不必引入函数：

解如果引入合适的函数f(x)=3x2-3arctanx2+2cosx3-2，则需要求出f（10）(0)。现在延续例2的思路展开幂级数。arctan t和cos t有现成的幂级数展开公式，利用这些公式将例3中括号内的表达式展开：

本例若按文献[1]中的公式处理，导数一直要求到10阶，且须核对参数k=(p-q)m-1方可选用4个结果中的第一个，而运用上述直接展开级数的方法则省去了这些繁琐环节，其优越性可见一斑。同样，当k≠(p-q)m-1时也无需核对参数，比如，将例3题目中括号前的n4改成n3，用级数展开求解也很方便：

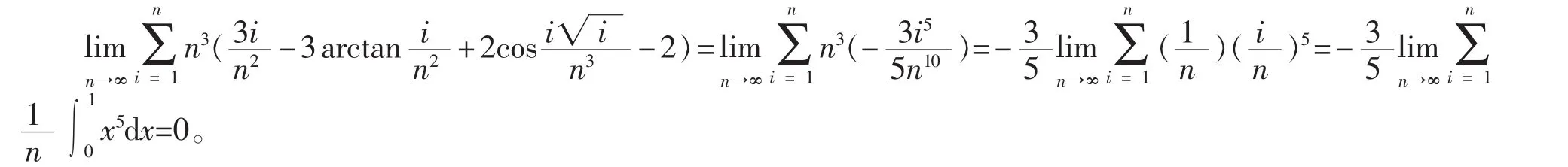
解利用sin t的幂级数展开公式，将括号内的表达式展开并略去余项，得：

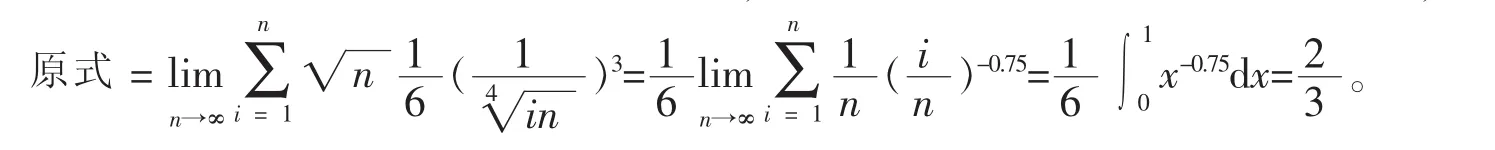
本文首先在理论上将文献[1]结果中的条件减弱，扩大了其适用的范围，更主要的是指出了定理的本质在于函数幂级数展开对极限式化简的支撑作用。因此，在处理这类和式极限问题时，不能拘泥于某个特定的公式，而须针对具体问题抓住关键特征，采用最合适的方法，才能取得事半功倍的效果。

[2]李冬梅.一类特殊和式极限的简便求法[J].鞍山师范学院学报.2007，19（1）：11-13.

[3]翟龙余.一类和式极限的求解[J].宜春学院学报.2008，30（4）：21-22.

[4]吴彬.极限运算中的局部无穷小等价替换规则[J].2011，25（4）：78-80.

（责任编辑：王晓燕）

Improvement of Calculating Formula and Method of a Sum Limit

LU Jian
(Nantong Vocational University，Nantong 226007，China)

Based on research findings of a common sum limit calculation，the paper draws and proves the conclusion that the formula is still workable under a weakened condition.Then it gives a simple way to carry out the expansion and the reminder rejection of power series in order to avoid the complexity of high order derivation in practical calculation.

sum limit；high order derivation；power series；reminder term

O171

A

1671-6191（2014）04-0032-02

2014-09-16

陆健（1979-），男，江苏南通人，南通职业大学讲师，研究方向为图论、数学教育与数学建模。

江苏省高等教育教学改革研究课题重点项目（编号2011JSJG085）；南通职业大学教改研究青年专项课题（编号2013-QN-02）。