基于牛顿插值法的电子互感器数据同步分析

刘同银，高 亮，朱 彤，张永东

(1.上海电力学院，上海 200090;2沂源县供电公司，山东淄博 256100)

常规变电站中电磁式互感器输出的是连续的模拟量，各路模拟量之间基本同步，只是传变角差有很小的误差，［1］在实际工程应用中可以忽略不计.随着IEC61850标准的不断发布和更新，智能化变电站得到了快速发展，其主要特点是一次设备智能化，全站信息数字化，信息共享标准化，高级应用互动化.特别是基于光学或电子学原理的电子互感器，是智能变电站中一次设备与二次设备的重要接口，是变电站智能化的关键设备.但由于其输出为离散的数字量，［2］使得各路数字量之间存在同步问题.

因此，研究电子式互感器的同步性具有非常重要的现实意义.

1 电子互感器时间同步方法

电子式互感器数据同步的两种常规方法为脉冲同步法与插值法.IEEE1588协议是特意针对网络测控系统等工业以太网提出的精确时钟同步协议，当前也有选用此协议完成采样值同步的详细方案.［3-4］

1.1 脉冲同步法

脉冲同步法的基本实现方案［5］如图1所示.合并单元通过内部时钟接收来自GPS或其他精确时钟的秒脉冲信号PPS;因为合并单元有多路输入输出接口，需要在合并单元内进行倍频处理.倍频处理后产生同步信号，经过硬接线连接到各路采集器的时钟接口，采集器根据同步信号进行采样，将采样值传回合并单元.此方法需要合并单元和采集器都有专门的时钟接口以及硬接线连接，结构复杂，成本较高.

图1 脉冲同步法实现方案

1.2 插值法

插值法是指在采样频率相同的前提下，各路数据采集系统进行非同步采样，每路测量量的采样值在合并单元内接收到时，由合并单元记录各采样值接收到的时标，然后利用插值法计算出在同一频率下各路测量量在同一时刻的插值采样值.［6-7］

应用此方法的前提是采样值从采集器到合并单元的传输延时Tdelay为已知量.一是各路测量量从采集器到合并单元打时标的延时是一个常数，即:

二是延时是个变量，但可以通过其他方法测量出来，即:

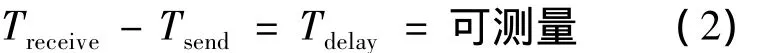
式中:Tsend——采集器的采样值发送时刻;

Treceive——合并单元收到采样值的时刻;

Tdelay——采样值从采集器到合并单元的传输延时.

此方法的优点是在保证采样频率相同的情况下，不需要同步信号来控制采样时刻，不需要相应的同步信号硬件电路，因此易于实现，成本较低.缺点是插值算法易产生误差，对不同的插值方法有不同的可靠性、计算量、精度及应用范围.

1.3 IEEE1588 协议

IEEE1588协议是一个工业以太网协议，是专门针对网络测控系统等提出的精确时钟同步协议(Precision Time Protocol，PTP)，其基本原理是用以太网中最精确的时钟去校正或同步其他时钟;同步过程是从时钟与主时钟相互交换4种不同含义的时间报文，取得不同报文的时间戳，计算出从时钟与主时钟的时间偏差，分为偏差修正和网络延时测量两个阶段.

其应用于合并单元的前提是:合并单元需要有支持此协议的以太网接口和交换机.文献［3］和文献［4］分别提出了一种采用IEEE1588实现合并单元同步采样的方案.

2 基于牛顿插值法的数据同步原理

合并单元在收到各路采样值后，根据传输延时计算出各路测量量的采样时刻，以采样值和采样时刻为两列生数据，采用相应的插值算法，计算出各路的插值函数，然后选取一固定时间序列，由求出的插值函数计算对应的函数值，作为新的采样值和采样时刻，因为采样时刻为固定的相同序列，故可以实现采样值的数据同步.

2.1 牛顿插值法原理

二次插值方法有两种:一是文献［6］采用的拉格朗日插值法;二是本文采用的牛顿插值法.以电压采样值为例，二次插值法可表述为:已知函数的 3 个连续离散采样值为［t0，u(t0)］，［t1，u(t1)］，［t2，u(t2)］.拉格朗日插值多项式［8］为:

牛顿法的插值多项式［8］为:

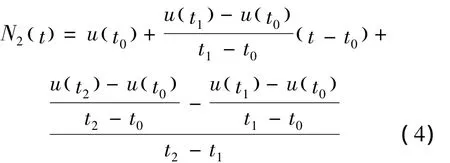
可知，在等间隔采样的情况下，令T=0.02/N，T为采样间隔，N为每周波采样点数;

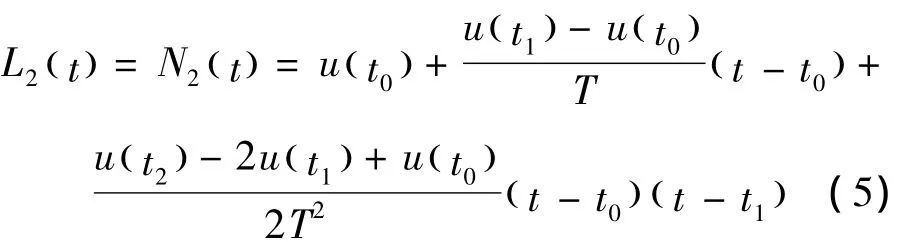
通过以上分析可知，在等距节点采样时，拉格朗日法与牛顿法的插值公式是完全相同的;但在非等距节点采样时，拉格朗日法需要进行9次乘法运算，而牛顿法只需要5次即可，其他计算量基本相同.因此，在高采样频率、高实时性的要求下，宜采用牛顿插值法.

2.2 牛顿插值法误差分析

由数值分析可知，根据插值多项式的惟一性，对于同一组数据上的n次插值多项式Ln(t)和Nn(t)，应有 Ln(t)=Nn(t)，因此其余项(即误差)是相等的，即:

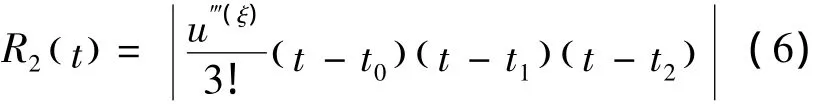
式中:R2(t)——插值误差;

u‴(ξ)——u( t)在 t= ξ处的三阶导数，ξ∈［t0，t2］.

由文献［6］可知，在电力系统暂态情况下，最大误差为:

电压统一的表达式可以表示为直流分量和各次谐之和:

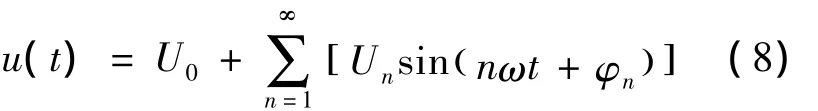
3 仿真与分析

本文以Matlab为仿真工具，对上述牛顿插值法进行了仿真验证.在编写仿真主程序时，其参数按不同的要求设置了可以自由决定每周期采样点数的变量SamplePointNum，测试开始的初始相位角度测试数目InitialPhaseNum，插值方法选择变量InterMethod，电力系统稳态和暂态变量State.采样值的间隔按SamplePointNum的大小决定，当SamplePointNum=48时，每周期采样48个点，则工频下采样点之间的时间间隔为5/12 ms.

在考虑采样速度和继电保护的要求下，本文主要采样频率为48点/周期，针对电力系统不同运行状态和不同同步方法分别进行了仿真.

3.1 稳态运行时采样值最大误差

稳态状态下，电压为:

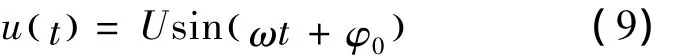
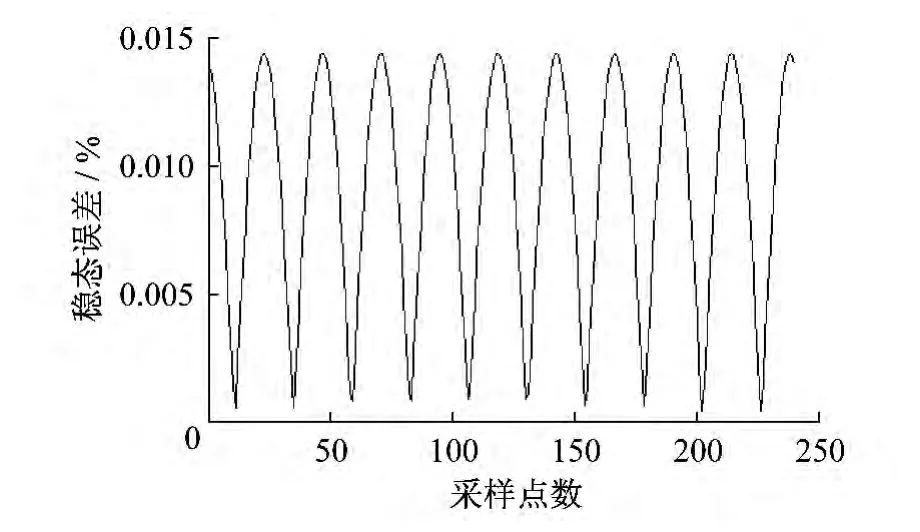
图2 牛顿法稳态最大误差

由图2和图3可知，一次牛顿插值的运行时间几乎为零，240次插值所用时间约为50 ms;而一次拉格朗日插值的时间约为15 ms，240次插值所用时间为4 s;牛顿法明显快于拉格朗日法.

图3 拉格朗日法稳态最大误差

3.2 暂态运行时采样值最大误差

暂态运行时，电压表达式与文献［6］相似，考虑了直流衰减分量、2次谐波分量和3次谐波分量，电压表达式为:

在仿真时可以自由设置各次谐波的初始相位值，仿真结果如图4和图5所示.

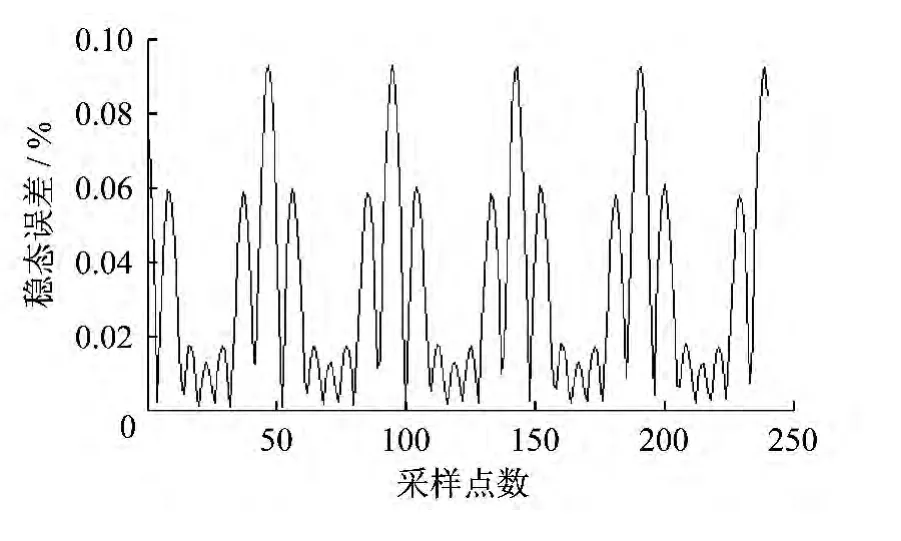
图4 拉格朗日法暂态最大误差值

图5 牛顿法暂态最大误差值

由以上图形可知，稳态和暂态情况下，牛顿法和拉格朗日法的精度几乎一致，并且与理论分析一致.不论是牛顿法还是拉格朗日法，暂态插值所用时间均大于稳态插值时所用的时间;同时，单次拉格朗日法所用时间是牛顿法的十几倍，将近一个周期，这对继电保护装置能否及时判断并切除故障极为重要.

3.3 非等距节点时数据同步

上述采样点均为等距节点，由于在实际运行中可能出现各种干扰，如采样器本身故障、电磁影响或电力系统故障等，使得采样器的采样值可能出现非等距采样，甚至丢失数据.因此，本文仿真了非等距采样时各种运行状态的插值最大误差，通过编程语句设置了3点之间的间距为不等间距，然后由循环来实现所有采样值的不等间距采样，两点间距可自由设置为N倍的等间距间隔.例如，当每周采样48点时，中间点的采样间隔可设为5N/12 ms，N=1.2时仿真结果如图6和图7所示.

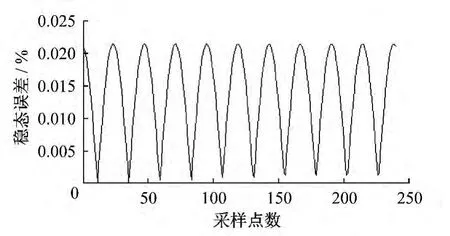
图6 非等距节点牛顿法稳态最大误差

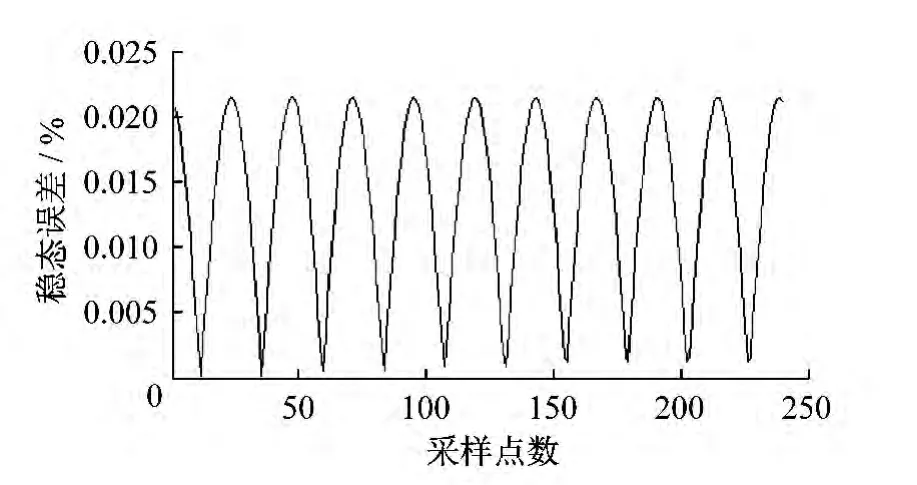
图7 非等距节点拉格朗日法稳态最大误差

由图6和图7可知，在非等距节点的情况下，牛顿插值和拉格朗日插值最大误差较等距节点时的插值误差大，因此在实际采样过程中，应尽量进行等距节点采样，但牛顿插值法和拉格朗日法仍均能满足实际需要，而且仿真显示，一次牛顿插值所用时间为48 ms，而拉格朗日法则需要3 s多，由此表明采用牛顿法插值进行数据同步的速度优于拉格朗日法的同步速度.

4 结语

本文研究了牛顿插值法在电子互感器中的数据同步问题:一是在理论分析的基础上，采用Matlab仿真工具，分别计算了稳态和暂态情况下牛顿法插值法与拉格朗日插值法的最大误差;二是在相同插值数据量的条件下，比较了两者插值速度的快慢;三是对非等距节点情况时的插值精度的最大误差进行了仿真.结果表明，在保证相同误差精度的情况下，尽量在等距采样点下采用牛顿法效果最好，而且牛顿插值算法较拉格朗日的速度快，在实时运行大量数据处理时效果会更好.

［1］ 曹团结，尹向根，张哲，等.电子式互感器数据同步的研究［J］.电力系统化及其自动化学报，2007，19(2):108-113.

［2］ 高翔.智能变电站技术［M］.北京:中国电力出版社，2012:45-48.

［3］ 殷志良，刘万顺，杨奇逊，等.基于IEEE1588实现变电站过程总线采样值同步新技术［J］.电力系统自动化，2005，29(13):60-63.

［4］ 韩颖，牟龙华，周伟.IEEE1588协议在合并单元中的应用与实现［J］.电力系统及其自动化学报，2012，24(3):16-21.

［5］ 刘琨，周有庆，张午阳，等.电子式互感器合并单元时间同步问题的解决方法［J］.电力系统通信，2006，27(3):71-75.

［6］ 乔洪新，黄少锋，刘勇.基于二次插值理论的电子式互感器数据同步的研究［J］.电力系统保护与控制，2009，37(15):48-52.

［7］ 董义华，孙同景，徐丙垠.基于三次样条插值理论的电子式互感器数据同步［J］.电力自动化设备，2012，32(5):102-107.

［8］ 同济大学计算数学教研室.现代数值计算［M］.北京:人民邮电出版社，2012:62-65.