配电网架空线路分段规划及运行研究

黄向红，王林海，汤 波

(1.国网温州供电公司，浙江 温州 325000;2.上海电力学院，上海 200090)

配电网是电能分配的末端环节，对整个电力系统网损水平、供电可靠性、用户电能质量的提高具有举足轻重的作用.［1］

10kV及以下电压等级的配电网具有闭环设计、开环运行的特点，在正常运行条件下，配电网通过降压变电站向一个树状网络的供电区域供电，单个供电段之间通过一个常合的自动或手动开关相接，而不同的供电区域之间则由平时断开的开关(联络开关)联系.在满足负荷需求的条件下，由于开关状态的不同组合，配电网可以存在多种供电路径，即形成了不同的网络结构.而网络结构的不同正是影响电网网损、供电电压质量、设备负载水平及供电可靠性的关键.因此，研究配电网开关优化以及对线路进行合理分段对提高配电网各项技术指标具有重要意义.配电网线路优化分段就是在所有可能的开关配置组合中，快速地找出一套既能满足网络运行条件(拓扑结构约束、线路容量约束等)，又能满足目标最优(网损最小、可靠性最高等)的开关配置方案.［2-7］

1 配电网及其接线模式

构成配电网网架结构的重要设备——中压线路多为架空网，其接线方式主要有单电源放射式、环式和多分段联络3种.

1.1 单电源放射式接线

该接线方式末端没有其他能够联络的电源，用户只能从一个方向获得电源，根据具体布线方式的不同，又分为完全放射式接线和树枝状放射式接线.树枝状放射式接线结构如图1所示.

图1 树枝状放射式接线

放射式接线的优点是接线简单、维护方便，但由于不分段，任一元件故障便会引起供电中断，故障范围较大，可靠性低.当负荷点沿线分布时，可采用树枝式接线，其干线可以分段，一般主干线分为2～3段.这种接线方式如果在末端发生故障，影响面少;若在前端发生故障，则影响面大，供电可靠性较差.

1.2 环式接线

该接线方式主要包括不同母线出线的环式接线及不同变电站出线的“手拉手”环式接线两种接线模式，如图2所示.

不同母线出线的环式接线方式接线清晰、运行比较灵活，可靠性比单电源放射式大大提高.电源故障时，通过切换操作可以保证供电，满足N-1要求;线路故障时，通过切换操作可以恢复正常段供电，但线路正常负载率低于50%，投资将比单电源放射接线有所增加.

不同变电站出线的“手拉手”环式接线的主干线两端都有电源，任何一端都可以供给全线负荷.由于采用了来自不同变电站的双电源供电，供电可靠性较高.但由于线路往往曲折而长度有所增加，且变电站的备用容量理论上需要留有30%的裕度，故其投资有所增大.

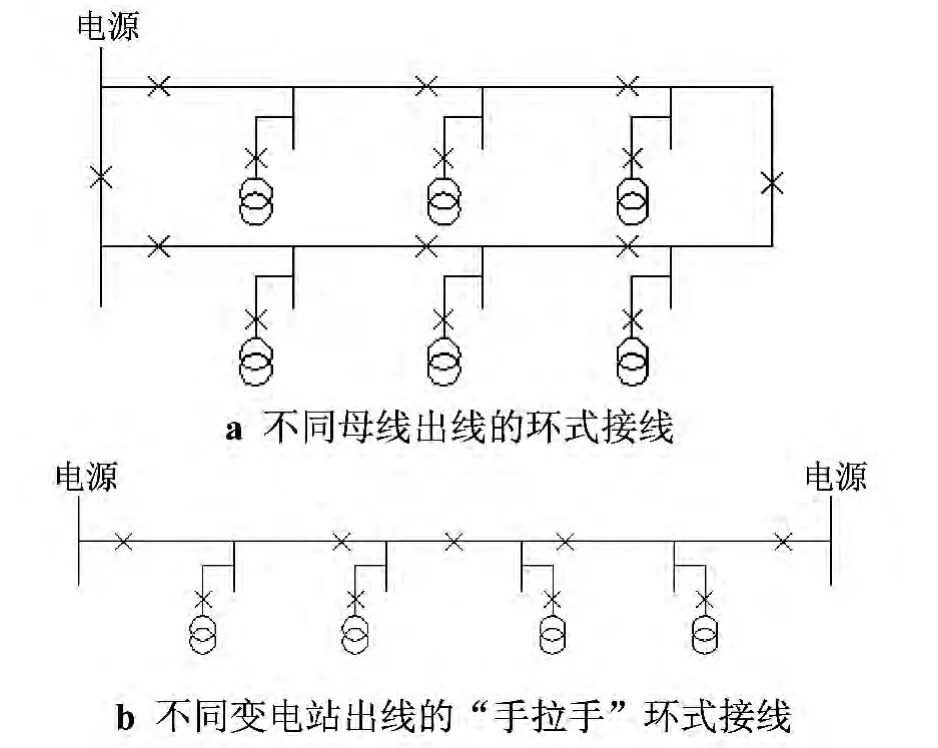
图2 环式接线模式

1.3 多分段联络接线

多分段联络接线是配电网在适当地点进行分段，形成多分段、多联络、多电源网格形(开式)运行的环网网络，如图3所示.

图3 三分段三连络接线

正常情况下，各条线路与邻近线路联络点的开关设备断开，网络开环运行.当线路故障或停电检修时，可以通过操作网络联络点和分段开关设备来调整供电范围，使停电范围缩小，提高供电可靠性.因此，目前这种接线方式得到了越来越多的推广.

为了提高运行的灵活性和可靠性，配电系统通常要在线路的合理位置设置相应数量的各种开关，并且通过这些开关不同的状态进行组合优化以改变网络的运行方式，满足配电网安全可靠的运行要求.本文针对这种具有多个开关设备(包括断路器、隔离开关、熔断器)的配电网进行开关的优化配置，通过开关的数量、位置及运行状态组合来挖掘配电网本身的强大潜力，尽可能以最小的投资成本获得最大的经济效益.

2 开关运行优化的数学模型

配电网线路分段优化是一个组合优化问题，具有离散型、非线性和高维性的特点.线路分段优化的数学模型包括开关投资及维护、用户停电损失等指标，经济模型包括开关投资及维护费用，可靠性模型包括用户停电损失.根据经济模型和可靠性模型，可得出综合模型.

2.1 经济模型

开关规划优化配置中的经济模型主要涉及开关的投资和运行费用.

由于设备使用寿命的不同，需选择等年值法进行投资评价，以避免设备寿命差异带来的影响.开关设备投资费用等年值为:

式中:Cs——开关设备总投资现值对应的等年值;

M——开关的类型(断路器、隔离开关、熔断器等)总数;

Nj——第j种开关增装的台数;

Csj——第j种开关单台投资现值(即现值单价);

Pj——第j种开关设备的使用寿命.

而每年开关的运行维修费用按其投资费用的百分数为:

式中:CM——开关设备每年的运行维修费用;

H——运行费用占投资的比例系数.

2.2 可靠性模型

可靠性模型主要由停电损失费用构成，根据可靠性评估方法得出系统每年停电损失费用为:

式中:CL——系统每年的停电损失费用;

LP——负荷点总数;

Tj——第j个负荷点有Tj种停电持续时间分类;

ENSjt——负荷点j第t停电持续时间对应的失电量;

CLOSSjt——负荷点j第t停电持续时间对应的单位停电损失.

2.3 综合模型

综合模型考虑将开关规划优化的经济性和可靠性目标合并，得到的目标函数为:

式中:Ka，Kb——经济性和可靠性权重因子，且Ka+Kb=1.

目标约束条件如下.

(1)资金约束为:

式中:Ck——系统投资等年值限额.

(2)可靠性约束为:

式中:R——某种开关配置模式系统的系统可靠性指标;

R0——给定的系统预定可靠性指标.

(3)节点电压和支路过负荷约束为:

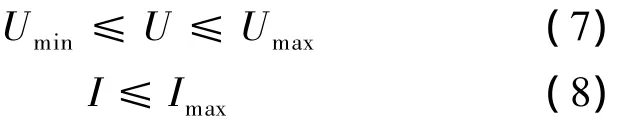
式中:Umin——节点电压最低值;

Umax——节点电压最高值;

Imax——支路安全电流约束.

(4)潮流约束为:

式中:A——节点支路关联矩阵;

P——馈线潮流向量;

D——负荷向量.

(5)拓扑结构约束为:保证在此开关状态下，网络结构为辐射状，并且不存在环路和孤立节点.

3 遗传算法的改进及应用

遗传算法［8-10］由于编码简单易行，从而得到了较多的应用.但在实际应用中，遗传算法基于开关开合或线路被选择与否进行编码，在遗传操作中会产生大量的不可行解，并且由于仅依靠遗传操作进行寻优，没有利用特定问题的特有性质，容易产生大量不可行解，且收敛速度慢，局部精确寻优能力差.本研究在选择操作中使用了最优保留操作，交叉和变异中使用了自适应的遗传算法，既保证了全局收敛性，又减少了迭代次数，增强了收敛的快速性.配电网开关运行优化的计算步骤如图4所示.

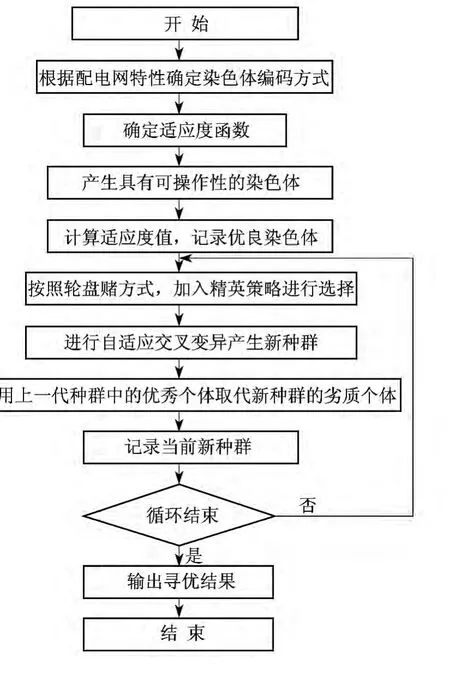
图4 线路分段优化程序流程

4 案例分析

对RBTS-Bus6系统［11］进行配电网线路分段优化，该系统是带有分支馈线的复杂中压配电系统，有83个节点，40个负荷点，2 938户用户，总平均负荷为10.715 5 MW.其中，设备单价为:断路器50 000$/组、隔离开关4 700$/组、熔断器610$/组;设备的使用寿命为20年，每年的运行维修费用按投资的3%计算;贴现率i为10%;单位停电损失费用为2.810 43$/kWh，供电可用率不低于99.8%.

优化中各主馈线首端均设断路器，各负荷支路进线端均设熔断器.计及所有断路器、隔离开关和熔断器数量，原系统年费用为269 760$.

分别针对几种典型模型进行计算.

(1)模型 1，即经济性模型，Ka=1，Kb=0.此模型意在寻找一次性投资最小的拓扑结构，其总费用只与开关个数有关，但其网架要满足约束条件中的可靠性约束，即要保证达到系统预定可靠性指标.

(2)模型 2，即可靠性模型，Ka=0，Kb=1.此模型意在寻找可靠性最高，即电量不足期望值最小的拓扑结构，但开关数量要求满足资金约束.

(3)模型 3，即综合模型，即 Ka=0.5，Kb=0.5，此模型综合考虑经济性和可靠性指标.

表1给出了3种模型的最优方案.由表1可以看出，对于模型1，由于追求一次投资最省，在供电可用率不得低于99.8%的要求下，其优化结果为断路器2个，隔离开关数量最少，仅为9个，但供电可用率为99.892%;模型2为可靠性最高模型，其优化结果为13个隔离开关，供电可用率达到99.948%;模型3的权重系数分别为0.5，即经济性和可靠性要兼顾，且处于同等地位.

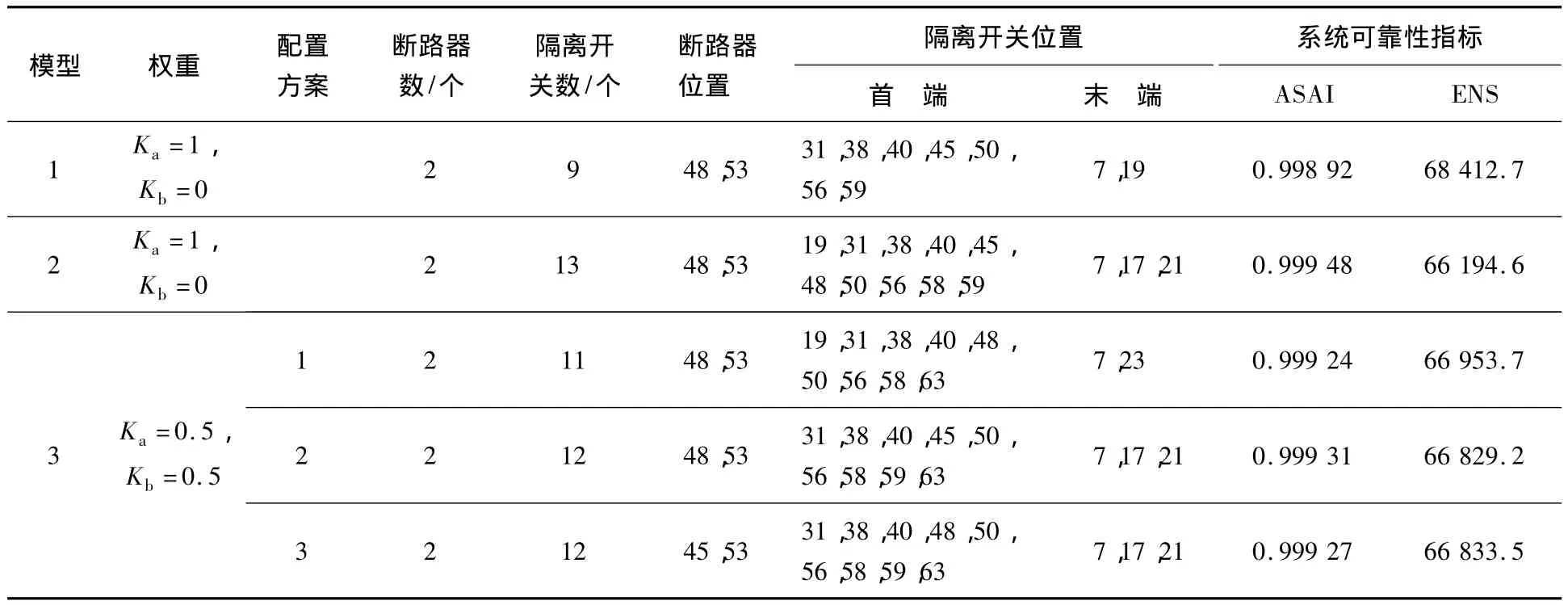
表1 RBTS-BUS6系统开关优化配置结果

表1给出了3个优化方案，其中方案1配置11个隔离开关，而方案2和方案3则分别在不同位置配置12个隔离开关，就其可靠性而言，方案2和方案3要高于方案1.

对于模型3的3种不同方案，表2给出了投资结果比较.由表2可以看出，方案1尽管可靠性略低于方案2和方案3，但系统综合费用最小，效益最高，为55 623$，比方案2高出343$.

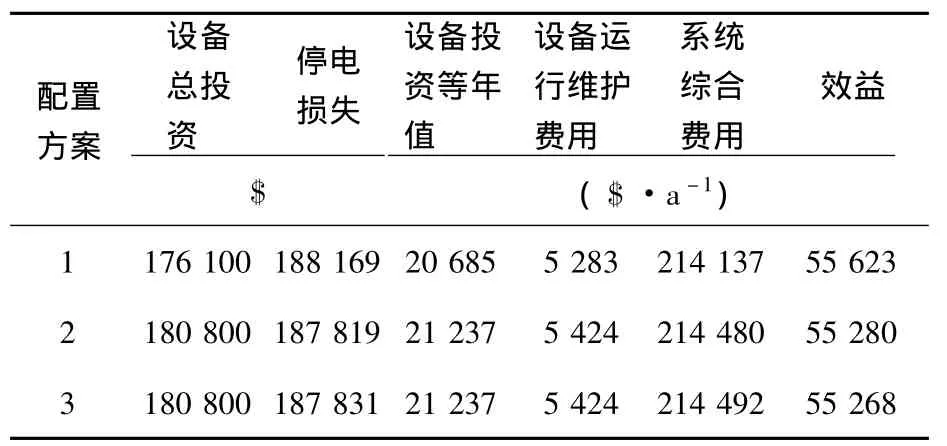
表2 基于模型3的RBTS-BUS6系统投资结果

表3列出了随机20次实验所搜到的结果，其中最优解搜寻率达到70%;若认为与最优解相对误差不足1‰的均为优秀解，则寻优率达80%.

表3 20次实验搜索结果

通过与简单遗传算法的对比，对本文提出的改进遗传算法的收敛效率进行检验.设置种群规模为80，最大迭代次数为80.根据大量实验表明，简单遗传算法进化效率较低，40代以内几乎搜不到最优解，而本文改进遗传算法在40代时已收敛.图5给出了最优解方案1的目标函数收敛过程.

图5 最优解的函数收敛过程

由图5可以看出，改进遗传算法的收敛速度比简单遗传提高很多.另外，增加迭代次数，本文算法对最优解的寻找能力继续增大，但普通遗传算法的搜寻能力改善并不明显.

5 结语

本文建立了配电网开关规划优化配置的经济模型、可靠性模型及综合模型，采用改进的遗传算法对模型进行求解.根据配电网运行的特点，优化了编码方案，采用支路交换法保证产生的初始种群为可行解，采用轮盘赌法和最佳保留策略改善选择操作的性能，采用随机定位两点交叉的算子进行交叉，采用随机产生的变异位置进行变异，且交叉率和变异率随搜索过程自适应变化，可大大减少计算量，提高计算效率.

［1］ 王守相，王成山.现代配电系统分析［M］.北京:高等教育出版社，2007:69-86.

［2］ 周彦佩.中压配电网开关优化配置［J］.四川电力技术，2006，29(2):10-11.

［3］ 万国成，仁震，荆勇，等.主馈线分段开关的设置研究［J］.中国电机工程学报，2003，23(4):124-127.

［4］ 谢开贵，刘伯私，赵渊，等.配电网开关优化配置的动态规划算法［J］.中国电机工程学报，2005，25(11):29-34.

［5］ TENG Jenhao，LU Channan.Feeder-switch relocation for customer interruption cost minimization［J］.IEEE trans.on Power Delivery，2002，17(1):254-259.

［6］ PARK Y M，LEE K H.Application of expert system to power system restoration on local controlcenter［J］.Electrical Power＆ Energy Systems，1995，17(6):407-415.

［7］ 余贻鑫，邱炜，刘若沁.基于启发式算法与遗传算法的配电网重构［J］.电网技术，2001，25(11):19-22.

［8］ 毕鹏翔，刘健，刘春新，等.配电网络重构的改进遗传算法［J］.电力系统自动化，2002，26(2):57-61.

［9］ 熊信银，吴耀武.遗传算法及其在电力系统中的应用［M］.武昌:华中科技大学出版社，2004:50-75.

［10］ 雷英杰，张善文，李续武，等.Matlab遗传算法工具箱及应用［M］.西安:西安电子科技大学出版社，2005:55-67.

［11］ COVANLAR S，GRAINGER J J，YIN H，et al.Distribution feeder reconfiguration for loss reduction［J］.IEEE Trans.on Power Delivery，1998，13(3):1 217-1 222.