基于干扰观测器的多光伏光柴混合系统协调控制研究

黄文宁，米 阳

(上海电力学院电气工程学院，上海 200090)

光伏新能源以其无污染、无噪声、取之不尽、用之不竭等优点而越来越受到人们的关注.［1-2］光柴混合供电［3］是解决我国偏远地区用电的重要途径.由于光伏新能源受天气变化的影响，其输出功率具有波动性、随机性、间歇性等特点，特别是多个光伏系统和柴油发电系统联合供电时，电源出力的波动性以及系统中负荷的不断变化可能会引起混合供电系统有功功率不平衡和频率大幅偏移，超出安全运行范围，需要采取适当的频率控制策略.［2-4］

近年来，关于如何降低可再生能源输出功率波动的研究已取得了一定的成果.文献［5］至文献［8］针对光伏最大功率跟踪控制进行了优化，减小了由于受天气条件的影响而产生的光伏输出功率的波动性，但是没有考虑微网中的负荷变化，并且没有直接针对系统频率偏差进行调节.文献［9］通过增加蓄电池储能设备来改善光伏系统的电能质量，使得光伏系统的输出变得更加平滑，但当光伏系统大规模应用时，需要安装大容量的蓄电池，将会导致光伏系统安装成本大幅增加，而且使用蓄电池会不可避免地带来环境问题.此外，还有学者专门设计了负载电阻来消耗波动的功率，但这并不能有效抑制功率波动.文献［3］提出了基于最小阶观测器［10-11］的光柴混合系统的多光伏协调控制策略，通过最小阶观测器预测系统负荷值，利用估计的负荷值来调节光伏系统的功率输出，从而减小了系统的频率偏差.但该文献中的最小阶观测器只适用于确定线性系统，而实际电力系统都是不确定的.

基于以上研究成果，本文提出了基于干扰观测器的多光伏协调控制策略.建立了光柴供电系统的模型，分析了太阳能发电的基本原理和特性.设计了干扰观测器，以估计混合电力系统中不断变化的负荷值.再根据估计的负荷值计算出负荷的变化值，利用负荷变化值调节各光伏系统的输出功率，进而实现对各光伏板出力的协调控制.最后，通过对10个光伏板在不同日照强度下的出力情况和频率变化进行了仿真分析.

1 光柴系统模型

本文研究的多光伏接入的光柴互补独立电力系统如图1所示.系统中有一台柴油发电机和10个光伏系统共同为负荷供电.假设所考虑的小型电力系统不与主网联接，即在孤岛状态下单独调度运行.

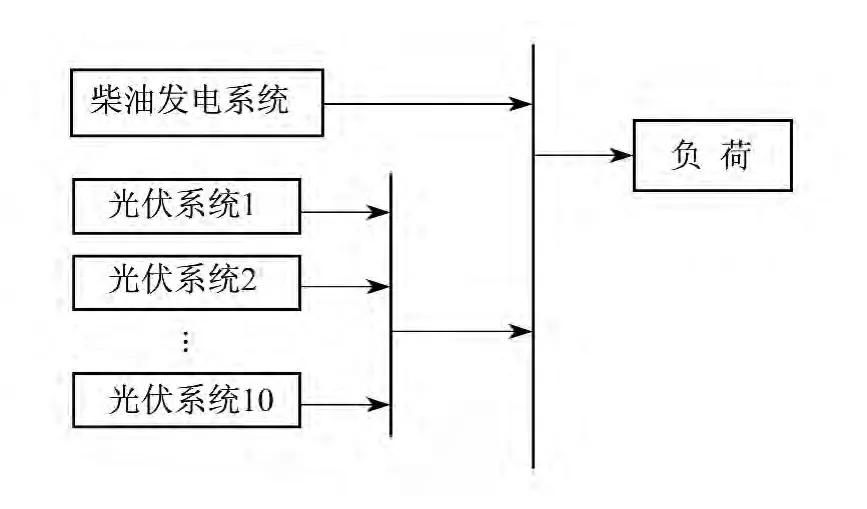
图1 光柴互补孤立电力系统示意

多光伏混合系统的动态结构如图2所示.其中包括柴油发电机、多光伏发电系统和负载.

图2 光柴混合系统动态模型

太阳能电池模块对设计逆变器和控制系统具有重要意义，可以用一个电流源模型表示，如图3所示.

太阳能电池模块的传统I-V特性可以表示为:

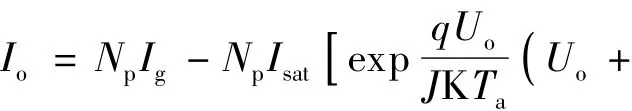
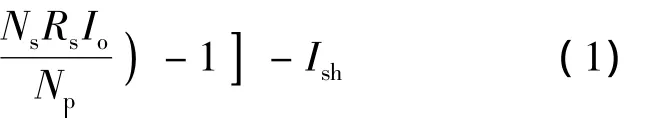
式中:Io，Uo——太阳能电池模块的输出电流和输出电压;

Ig——光生电流;

Isat——光电池反向饱和电流;

q——电子电量;

K——波尔兹曼常数，1.38 ×1023J/k;

J——二极管理想因子;

NP——并联电池数;

NS——串联电池数;

Ish——光电池内阻电流.

图3 太阳能电池模块的等效电路

太阳能电池模块的饱和电流Isat随温度变化的情况可以表示为:

式中:Ior——温度为Tref时的饱和电流;

Ta——光伏阵列的温度;

Tref——参考温度;

Eg——材料跨越能阶所需能量;

It——短路电流温度系数;

Isc——太阳能电池模块的短路电流.

光电池内阻电流可以表示为:

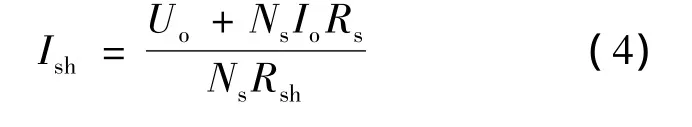
式中:Rsh——太阳能电池模块内阻.

光伏的输出功率为:

2 协调控制命令

图4为根据式(1)至式(5)得出的I-V和P-V特性仿真曲线.［5］可以看出，光伏阵列受日照强度的影响，其输出特性是非线性的.

为了减小混合系统的频率偏差，需要根据系统中负荷的变化来协调各光伏系统的出力，而电力系统中的负荷是不断变化和不确定的，因此本文设计了干扰观测器来估计不断变化的负荷值.由图2可知，电力系统的状态空间模型满足如下方程:

其中:

式中:x(t)——状态向量;

x1——频率偏差;

x2——柴油发电机输出功率Pd;

x3——调速器输出;

x4——积分控制量.

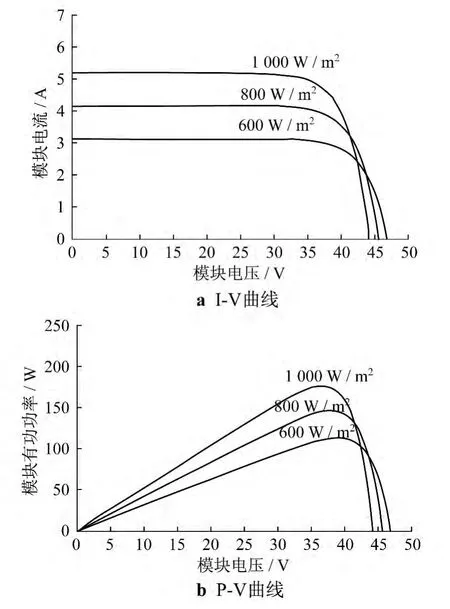
图4 太阳能电池模块特性曲线

令f(t)=HPL，则系统模型简化为:

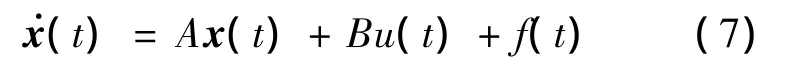
为了设计干扰观测器，构造原系统的增量模型如下:

对应干扰观测器满足如下状态方程:

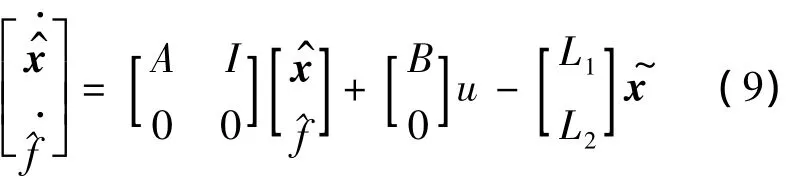
I——4 ×4 单位矩阵;

L1，L2——观测器的增益矩阵，L1=A+2Λ，L2=Λ2.

由式(8)和式(9)可得观测误差方程为:

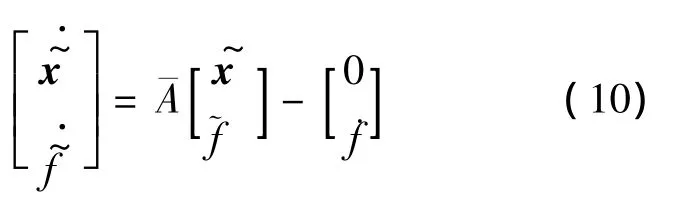
其中:

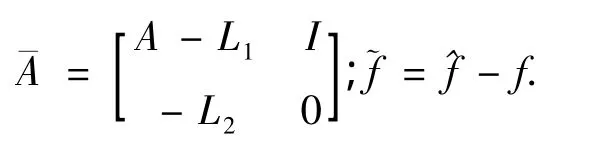
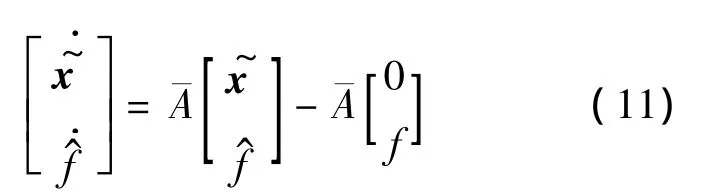
由于系统矩阵A，B，H是已知的常数矩阵，分别为:

因此观测器矩阵应满足:

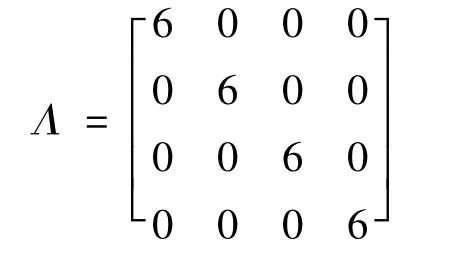
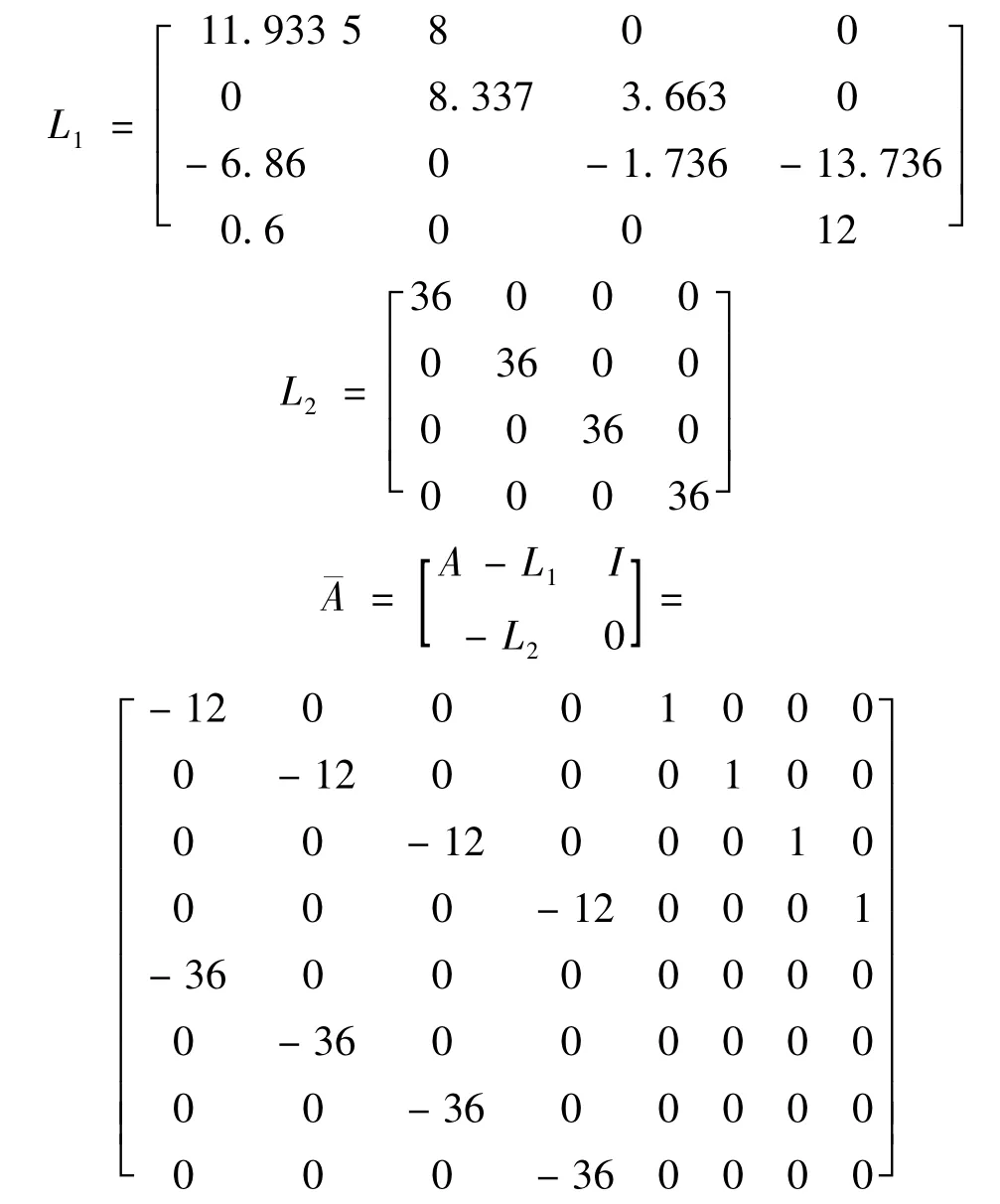
可见，设计的干扰观测器能够精确地估计出系统中的负荷扰动值.

为了减小系统的频率偏差，需要根据负荷变化来协调各光伏板的出力.下面根据估计的负荷值，设计多光伏系统的中央控制命令和局部控制命令.利用设计的干扰观测器得到负荷的估计值，则负荷变化为:

式中，积分区间T=100 s.

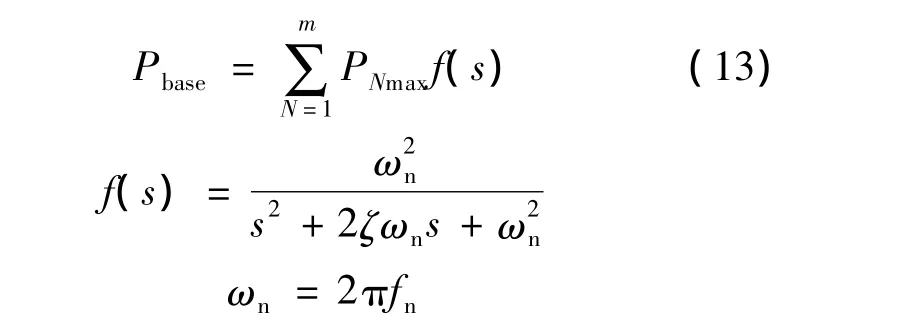
式中:m——光伏板的个数;

ζ——阻尼系数，取为 0.707;

fn——自然频率，取为50 Hz;

PNmax——第i个光伏板最大功率.

中央控制命令可表示为:

下面分析各个光伏板的局部控制命令.图2中各光伏板的混合功率PA可表示为:

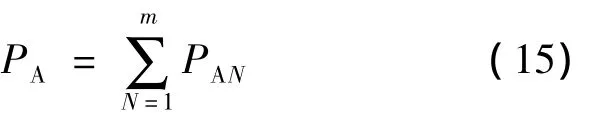
式中:PAN——各光伏板输出功率.

本文使用调整系数β来协调中央控制命令和局部控制命令，β可表示为:

式中:PNmax——第 N个光伏系统 MPPT的输出功率.

由此可知，各光伏板的局部控制命令可表示为:

3 光伏系统模块

3.1 光伏阵列功率模块

光伏模块的性能极易受天气条件，特别是太阳辐射和光伏模块温度的影响.根据实际情况将仿真模型进行适当简化，估计实际的光伏模块在不同操作条件下的性能，通过5个参数(α，β，γ，Rs，nMPP)模拟环境因素对光伏模块性能的非线性影响.光伏模块的最大输出功率可以表示为:

式中:nMPP——光伏模块在最大功率点处的理想条件，1＜nMPP＜2;

UOC，UOC0——光伏模块温度为T和T0时的开路电压;

T，T0——两个光伏模块的温度，K;

G，G0——两个光伏模块的太阳幅照强度;

ISC，ISC0——光伏模块温度为T和T0时的短路电流;

q——充电电子的光度，1.6 ×1019C;

Rs——串联电阻，Ω;

α——光伏电流的非线性效应;

β——光伏模块系数;

γ——考虑所有温度与电压影响的非线性因素.

详细的参考数据如表1所示.

表1 参考数据

仿真模型可用于光伏模块的性能预测，其参数估计结果如表2所示.

表2 参数估计结果

光伏模块是光伏系统的基本能量转化单位，本文考虑的是Ns×Np的光伏模块，其最大输出功率为:

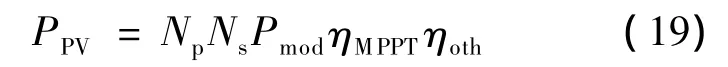
式中:ηMPPT——最大功率点跟踪效率，随工作条件的变化而变化，取95%;

ηoth——损耗因子，如电缆电阻和累积灰尘等所造成的损耗.

因此，若已知太阳辐照强度和光伏模块的温度，就可以预测光伏系统的输出功率.

3.2 光伏发电系统

光伏发电系统原理如图5所示.由图5可知，光伏发电系统包含太阳能电池阵列、升压斩波电路、MPPT控制器、双向PV换流器，以及发电系统输出功率参考值.

图5 光伏发电系统

4 仿真算例

本文使用10个额定功率为22.5 kW 的光伏板，相关参数见文献［6］，仿真时间为1 800 s.负荷的实际值和估计值如图6所示.可以看出，系统的负荷在800 s和1 100 s时发生了很大的波动.图7为相应时间内负荷的变化情况.图8为光伏板1，光伏板5，光伏板9的日照强度.图9为光伏板的基准功率，可以看出该功率一直在0.12左右波动.图10至图13为不同光伏板的出力变化.图14为频率偏差曲线.由图10至图13可以看出，在功率输出参考命令中引入负荷变化后，各光伏板的出力波动明显减小.由图14可知，采用本文方法得到的系统输出频率偏差远小于传统方法得到的频率偏差.

图6 负荷功率的实际值和估计值

图7 负荷变化情况

图8 3个光伏板的日照强度

图9 光伏板的基准功率

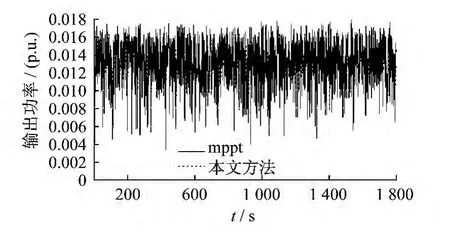
图10 光伏板1的输出功率

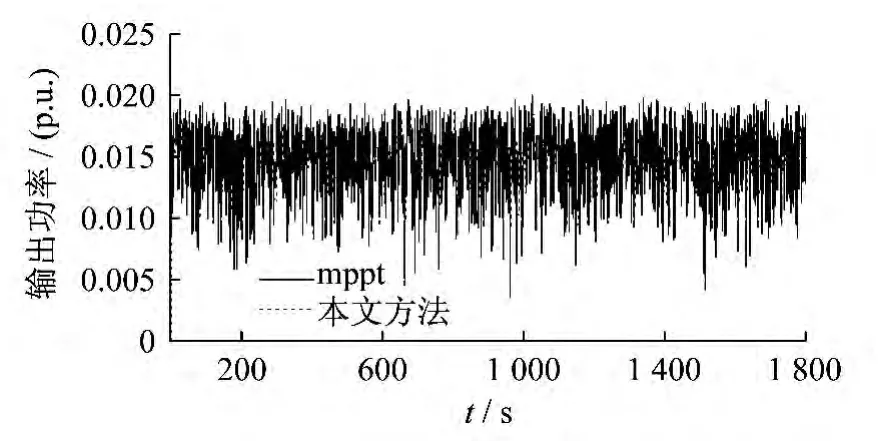
图11 光伏板5的输出功率

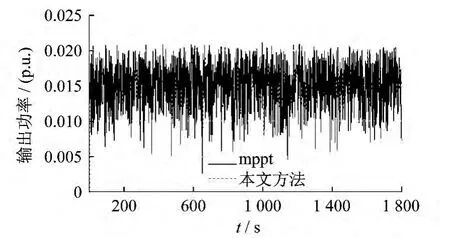
图12 光伏板9的输出功率

图13 10个光伏板的输出功率

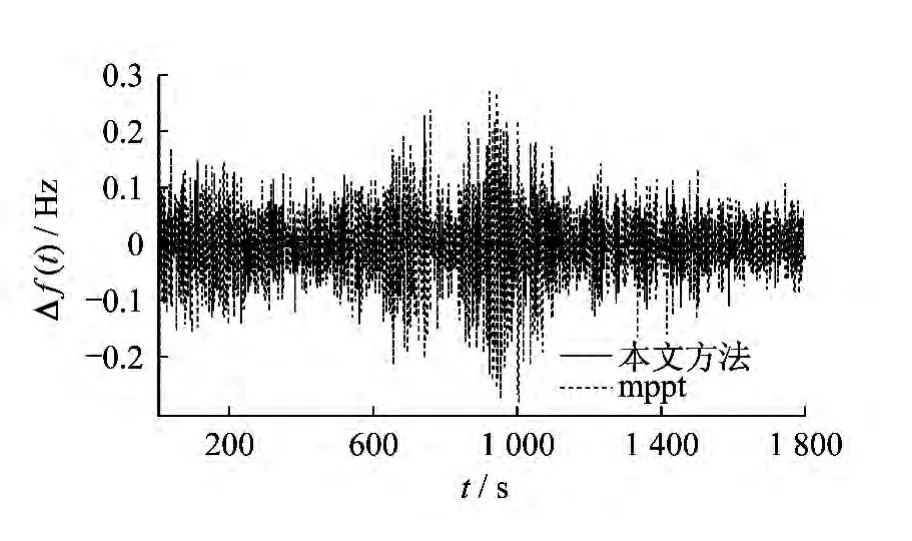
图14 频率偏差曲线

5 结论

(1)提出了基于干扰观测器的多光伏光柴混合系统协调控制方法，利用干扰观测器估计系统中的负荷值，计算负荷的变化值，并将负荷变化值应用到光伏输出功率参考值的设定中.

(2)与每个光伏系统只采用最大功率跟踪控制的多光伏系统的供电效果进行了对比.仿真结果证明，本文所提出的协调控制方法减小了光柴混合系统的频率偏差，并且各个光伏系统也获得了较大的功率输出.

［1］ WOYTE A，THONG VV，BELMANS R，et al.Voltage fluctuations on distribution level introduced by photovoltaic systems［J］.IEEE Transactions Energy Conversion，2006，21(1):202-209.

［2］ ASANO H，YAJIMA K，KAYA Y.Influence of photovoltaic power generation on required capacity for load frequency control［J］.IEEE Transactions Energy Conversion，1996，11(1):188-193.

［3］ TOMONOBU Senjyu，MANOJ Datta，ATSUSHI Yona，et al.A control method for small utility connected large PV system to reduce frequency deviation using a minimal-order observer［J］.IEEE Transactions on Energy Conversion，2009，24(2):520-528.

［4］ WIEMKEN E，BEYER H G，HEYDENREICH W，et al.Power characteristics of PV ensembles:Experiences from the combined power production of 100 grid connected PV systems distributed over the area of Germany［J］.Solar Energy，2001，70(6):513-518.

［5］ FEMIA N，PETRON G，SPAGNUOLO G，et al.Optimization of perturb and observe maximum power point tracking method［J］.IEEE Trans.Power Electron，2005，20(4):963-973.

［6］ HUA C，LIN J，SHRN C.Implementation of a DSP controlled photovoltaic system with peak power tracking［J］.IEEE Trans.Ind.Electron，1998，45(1):99-107.

［7］ 周念成，闫立伟，王强钢.光伏发电在微电网中接入及动态特性研究［J］.电力系统保护与控制，2010，11(14):119-127.

［8］ INA N，YANAGAWA S，KATO T，et al.Smoothing of PV system output by tuning MPPT control［J］.Elect.Eng.Jpn，2005(2):10-17.

［9］ WANGER R.Large lead/acid batteries for frequency regulation，load levelling and solar power applications［J］.J.Power Sources，1997，6(7):163-172.

［10］ LUENBURGER D G.An introduction to observer［J］.IEEE Trans.Autom Control，1971，16(6):596-602.

［11］ MIN L C，SHING C S.Control of power systems using minimal-order observers［J］.Computersand Electrical Engineering，1980，7(3):211-215.