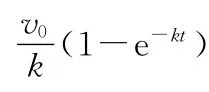浅谈物体速度的变化对位移是均匀的变速运动

张 军

（江苏省镇江市丹徒区教育局教研室，江苏 镇江 212001）

1 问题提出

伽利略对变速运动问题研究时，坚信自然界的规律是简洁明了的.他从这个信念出发，猜想落体一定是一种最简单的变速运动，而最简单的变速运动，它的速度应该是均匀变化的.但是，速度的变化怎样才算“均匀”呢？他考虑了两种可能；一种是速度的变化对时间来说是均匀的，即v与t成正比，另一种是速度的变化对位移来说是均匀的，即v与x成正比.后来发现，如果v与x成正比，将会推导出十分复杂的结论.所以，伽利略开始以实验来检验v与t成正比的猜想是否是真实的…….

以上文字是人教版高中物理必修1第2章第6节——“伽利略对自由落体运动的研究”中一些内容.伽利略指出：如果v与x成正比，将会推导出十分复杂的结论.那么，十分复杂的结论究竟是什么呢？

2 理论推导

设某一物体做速度的变化对位移是均匀的运动.则（1）物体的位移如何随时间变化？（2）物体的速度如何随时间变化？（3）此物体受力的特点如何？

解析：（1）由题意可得，v与x成正比，写成等式

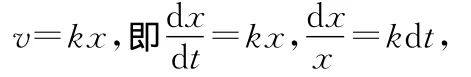
积分可得

将t＝0时，x＝x0代入得c2＝x0，所以物体的位移随时间变化的表达式为

（2）对（1）式进行求导

其中v0＝kx0是t＝0时物体的速度，物体的速度随时间变化的表达式为

（3）由v＝kx得

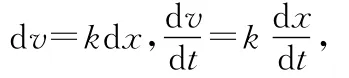
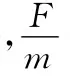
即物体所受合外力与物体的速度成正比.

由（2）式得物体所受力随时间变化的表达式为

由（4）式可知t＝0时物体所受力F0＝kmv0.因为（3）式可知物体所受合外力与物体的速度成正比，如果t＝0时物体的初速度为v0＝0，则F0＝0，导致加速度a0＝0，物体就不能运动，所以t＝0时，初速度和初位移都不能为0，这时加一合外力与物体的速度成正比，这样物体就做“速度的变化对位移是均匀的”运动了.

3 实际应用

（1）物体所受合外力的大小与物体的速度成正比，方向和速度方向一致.

日常生活中很难见到物体所受合外力与物体的速度成正比的动力，现举一例.

例1.一汽车额定功率为100kW，质量为5000kg，设汽车的功率与速度之间的关系为P＝62.5v2，阻力不计.求：

①汽车保持这样功率与速度关系运动所能达到的速度；

② 上述过程中汽车所做的功；

③ 汽车保持这样功率与速度关系运动的距离.

解析：① 将P＝100kW代入P＝62.5v2，得维持P＝62.5v2所达到的最大速度v＝40m/s.

② 忽略汽车启动的速度，即取v0＝0，则由v0＝kx0得，启动的位移x0＝0.汽车所做的功

③ 由P＝62.5v2，P＝Fv得F＝62.5v，即物体所受合外力与物体的速度成正比.

再由牛顿第二定律得

当然，应用理论推导中得到的公式（1）或（2），还可以求出上述过程所经过的时间.

（2）物体所受力的大小与物体的速度成正比，方向和速度方向相反.

物体所受力的大小与物体的速度成正比的阻力，这类例子较多，如① 一小球在以一初速度在水平光滑的平面上运动，设所受阻力满足F＝－kv；② 一小球以一初速度竖直进入某油液中，设小球的密度与油液密度相等，所受阻力满足F＝－kv；③ 一金属棒垂直水平导轨放置，以一初速度做切割磁感线运动，所受的安培力也满足F＝－kv.

下面以金属棒受安培力为例举一例说明.

图1

例2.如图1所示，水平光滑的平行金属导轨，左端接有电阻R，匀强磁场B竖直向下分布在导轨所在的空间内，质量一定的金属棒PQ垂直导轨放置.今使棒以一定的初速度v0向右运动，当其通过位置a、b时，速度分别为va、vb，到位置c时棒刚好静止.设导轨与棒的电阻均不计，a、b与b、c的间距相等，则金属棒在由a→b和b→c的两个过程中

（A）棒都做匀减速运动，且加速度相等.

（B）通过棒截面的电荷量相等.

（C）回路中产生的电能Eab＝3Ebc.

（D）棒通过a、b两位置时va＞2vb.

解析：对于（A）、（B）两选项，由于学生平时练的较多，容易判断出（A）错、（B）对，这里就不做解答.

对于（C）、（D）两选项，就要具体算一下了.对棒进行受力分析，由牛顿第二定律得

即v与x成正比.同理可得

由能量转化与守恒定律得，由a→b和b→c的两个过程中，回路中产生的电能Eab＝3Ebc.可得选项（C）正确、（D）错误.

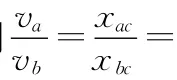
拓展分析：

即速度随时间做指数衰减.图像如图2所示.由

解得

即位移随时间变化关系，图像如图3所示.

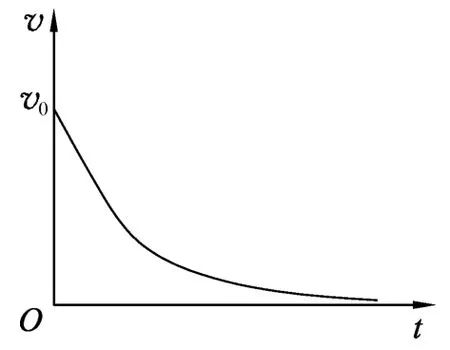
图2

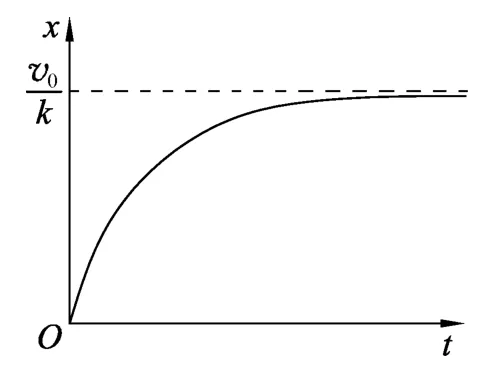
图3

由（4）式可求出最大位移